Jouer à Tetris en AR

Il m'est venu à l'esprit une petite idée étrange que la maison pourrait être une bonne plate-forme pour jouer à Tetris. Non loin de moi, il n'y avait qu'un seul bâtiment adapté à cela. Le résultat peut être vu dans la vidéo:


Le projet est mis en œuvre à un niveau assez bas, sans utiliser de solution toute faite.

Code source

Le plus souvent, ils utilisent 2 options pour implémenter la réalité augmentée:

• sans marqueur, c.-à-d. la position de la caméra est déterminée par le mouvement des points clés de son flux vidéo;
• l'image comme marqueur par rapport auquel la position de la caméra est.

Ces implémentations ne nécessitent pas de préparation spéciale ni de conditions particulières.

Il existe une autre option d'implémentation - pour reconnaître un objet spécifique et l'utiliser comme marqueur. Cela nécessite au moins sa présence, mais permet de le contrôler visuellement. L'une des méthodes d'une telle reconnaissance est la détection d'un objet par les bords. Il a des limites - l'objet marqueur doit avoir des bords clairement définis, c'est-à-dire l'objet doit très probablement être solide.

Ou les bords doivent être clairement délimités, comme l'éclairage de ce bâtiment:



On peut voir que le rétro-éclairage peut facilement être séparé dans l'image et utilisé pour la détection.

Implémentation

Le Qt. Ce framework vous permet de travailler sur différentes plateformes et en même temps en C ++. Puisque les performances sont importantes pour nous, les pros semblent être un choix évident.

Bien que Qt ne fonctionnait pas très bien avec Android (lancement long, le débogage était désactivé), mais tout cela était nivelé par la possibilité de déboguer l'algorithme sur le bureau.

Des graphiques en trois dimensions ont été visualisés sur l'OpenGL brut intégré dans Qt.

Le travail avec la caméra a été effectué via Qt. Une vidéo a été enregistrée pour le débogage, et c'était assez pratique pour remplacer le flux vidéo de la caméra par un flux vidéo à partir d'un fichier.

La sortie a été effectuée via des outils qml. Se faire des amis qml et OpenGL n'a pas été sans problème, mais nous ne nous attarderons pas là-dessus.

Pour le traitement d'image, la bibliothèque OpenCV est connectée.

Algorithme de suivi

Passons maintenant à la partie la plus intéressante - l'algorithme de suivi d'un objet le long de ses bords.
Et commencez par mettre en surbrillance les bords de l'image. Tous les bords dans notre cas ont la forme de lignes droites, donc la première pensée qui vient à l'esprit est d'utiliser un détecteur de ligne. Les transformées de Hough pourraient être utilisées comme détecteur de ligne. Cependant, cette méthode ne me semble pas très vraie, car la transformée de Hough est assez chère, et ce détecteur n'est pas très fiable (c'est subjectif, peut-être que tout dépend de la tâche).
Au lieu de cela, allons d'une manière différente et plus générale. Nous ne prendrons pas en compte le fait que nos lignes sont droites, mais nous travaillerons simplement sur une image binaire. La présence de bords sera encodée dans l'image binaire. C'est-à-dire un pixel avec une valeur de zéro signifie qu'il y a un bord à cet endroit, la valeur du pixel est supérieure à zéro - il n'y a pas de bord. Une telle image peut être obtenue à l'aide d' un détecteur de limites Canny ou à l'aide d'une simple transformation de seuil . Ces algorithmes peuvent être trouvés dans OpenCV.

Toujours dans OpenCV, il y a une autre fonction qui nous est utile maintenant - distanceTransform , qui prend une image binaire à l'entrée et donne une image à la sortie, dans les pixels dont la distance au pixel zéro le plus proche est codée.

Supposons maintenant que nous ayons déjà la première bonne approximation de l'emplacement de notre modèle. Ensuite, nous décrivons la fonction d'erreur, qui décrit dans quelle mesure les bords de notre approximation ne coïncident pas avec les bords de l'image résultante. En utilisant l'image de distanceTransform, nous pouvons déjà le faire. Et puis nous exécutons l'algorithme d'optimisation de fonction, ne modifiant que notre approximation de la position de l'objet dans l'espace. Par conséquent, notre approximation devrait décrire assez précisément la position réelle de l'objet.
En conséquence, l'algorithme peut être divisé en deux étapes:

1. Prétraitement d'image - binarisation, filtrage et utilisation de la fonction distanceTransfrom.
2. Suivi - optimisation de la fonction d'erreur.

Prétraitement d'image

À ce stade, vous devez mettre en évidence les bords de l'image. Vous pouvez utiliser le détecteur de limites Canny, mais dans notre cas, la conversion de seuil habituelle ou sa version adaptative fonctionne mieux (dans OpenCV, ce sont des fonctions de seuil ou adaptiveThreshold). Il est clair qu'il y aura du bruit sur une telle image, un filtrage est donc nécessaire. Faisons-le comme suit - sélectionnez le contour à l'aide de la fonction OpenCV findCountours et supprimez les segments trop petits ou pas assez comme une ligne.

Le résultat du traitement peut être vu dans l'image:



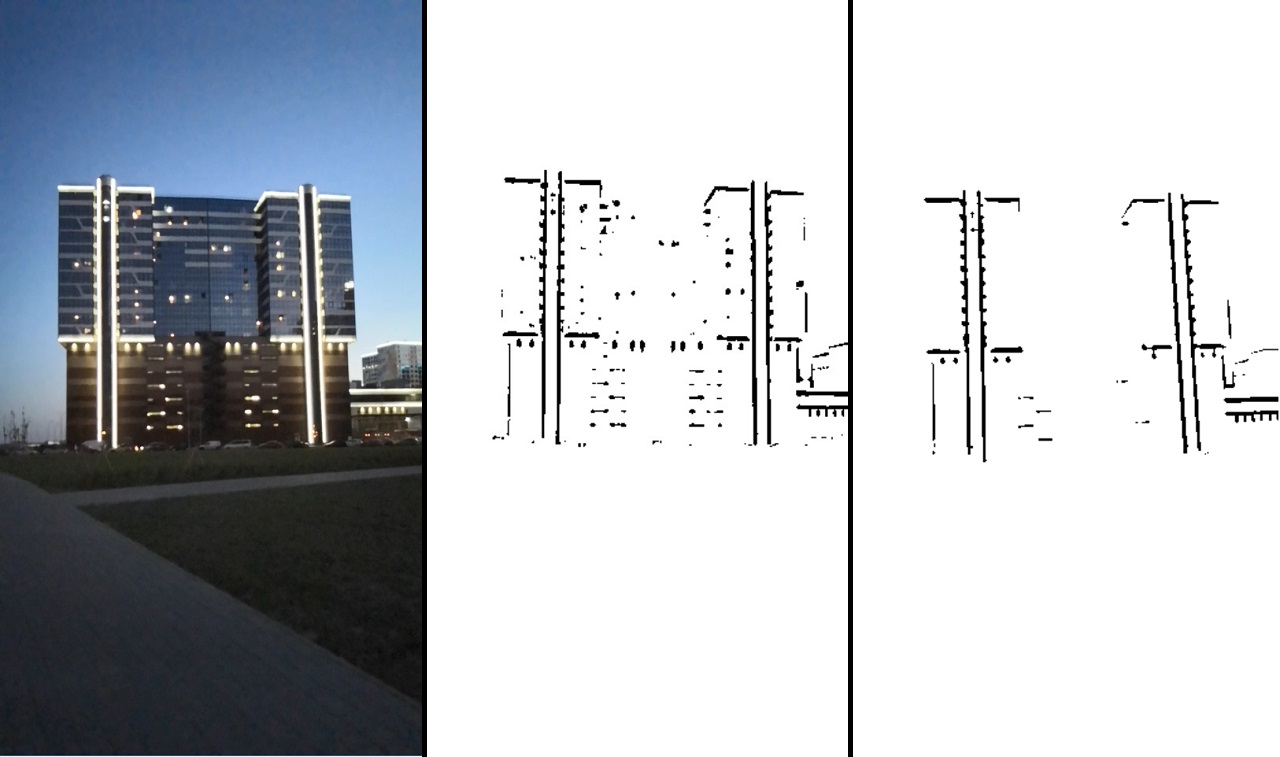
Constamment: l'image d'origine -> après la transformation du seuil -> après le filtrage.

Cette image nous dit déjà assez clairement où il y a le bord droit et où non. Après cela, nous utilisons la fonction distanceTransform, et en conséquence, nous aurons des informations sur la distance de chaque point par rapport au bord. L'image résultante est notée comme .

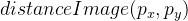
Voici à quoi cela ressemble s'il est normalisé et visualisé:



Ensuite, nous aurons besoin de quelques outils mathématiques.

Algorithme d'optimisation de fonction

L'optimisation des fonctions consiste à trouver le minimum d'une fonction.

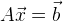
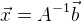
Si nous avons affaire à un système d'équations linéaire, alors trouver un minimum est assez simple. Imaginez le système d'équations sous forme matricielle: , alors notre solution: . Si nous avons un système d'équations surdéterminé, alors nous pouvons utiliser la méthode des moindres carrés : .

Si notre fonction est non linéaire, alors la tâche devient plus compliquée. Pour trouver le minimum, vous pouvez utiliser l'algorithme de Gauss-Newton . L'algorithme fonctionne comme suit:

1. On suppose que nous avons déjà une première approximation de la solution que nous allons affiner itérativement.
2. En utilisant l'expansion de Taylor, nous pouvons approximer notre fonction non linéaire linéaire au point d'approximation actuel. Nous résolvons le système linéaire d'équations résultant par la méthode des moindres carrés, obtenant 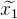. Par conséquent, la solution résultante ne sera pas une solution, mais elle sera plus proche que l'approximation actuelle.
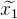3. Remplacer l'approximation actuelle a reçu la décision et passez à l'étape 2. Donc, répétez jusqu'à ce que la différence entre et ne sera pas inférieure à une certaine valeur.

Analysons plus en détail l'algorithme.

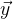
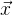
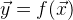
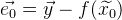
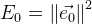
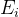
Soit - fonction de travail, - un vecteur de valeurs de fonction précédemment connu. Avec la solution parfaite à l'équation l'énoncé suivant est vrai . Mais nous n'avons que son approximation . Le vecteur d'erreur de cette approximation est alors noté: . Une erreur générale de la fonction sera: . Maintenant, trouver de tels à quel atteindra un minimum, nous obtiendrons une meilleure approximation de la solution .
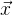
À partir de l'approche nous allons l'approximer itérativement, en obtenant à chaque itération . Pour ce faire, nous avons besoin de chaque itération pour calculer la matrice de Jacobi pour la fonction pour l'approximation actuelle, constituée de dérivées de notre fonction:

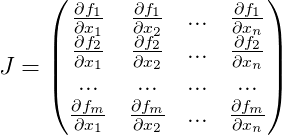
Et l'approximation suivante est donnée comme suit: .
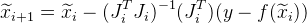
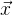
Souvent, les tâches sont construites de telle manière que nous avons un grand nombre de données indépendantes les unes des autres (uniquement à partir des valeurs ) En conséquence, la matrice générale de Jacobi est très clairsemée. Il existe un moyen d'optimiser les calculs.
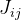
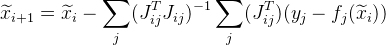
Supposons qu'une fonction commune soit calculée à partir d'un ensemble de points. A partir du jième point, nous obtenons . Au lieu de calculer la matrice de Jacobi pour la fonction entière, nous calculons la matrice de Jacobi spécifiquement pour et le dénoter comme: . Ensuite, l'approximation suivante sera donnée comme suit: . De plus, cette modification vous permet de paralléliser les calculs.
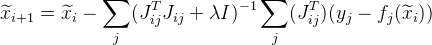
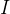
Il peut arriver que la valeur suivante donnera une plus grosse erreur que . Pour résoudre ce problème, vous pouvez utiliser une modification de l'algorithme - l'algorithme de Levenberg-Marquardt . Ajouter de la valeur dans notre formule: où Est une matrice unitaire. Valeur sélectionnés comme suit:

• tout d'abord, il a une valeur plutôt faible (telle que l'algorithme converge);
• alors si une erreur pour plus que , puis augmentez la valeur et essayez de calculer l'erreur pour encore.

Plus la fonction est non linéaire plus la valeur doit être élevée . Cependant, plus la valeur est élevée , plus l'algorithme converge lentement.

Nous complétons l'algorithme lorsque différent de assez petit et prendre comme solution.

L'algorithme est assez universel et peut être utilisé pour une variété de tâches.

Modèle de suivi mathématique

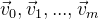
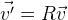
Puisque nous avons affaire à des coordonnées dans l'espace, il est clair que nous devons être capables de manipuler ces coordonnées. Supposons que nous ayons un ensemble de points . Et nous devons les faire pivoter autour du point avec des coordonnées nulles. La façon la plus simple serait probablement d'utiliser la matrice de rotation R , qui décrit la rotation nécessaire: . Si nous devons déplacer les points, il suffit d'ajouter le vecteur t souhaité: .
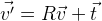
Ainsi, vous pouvez modifier arbitrairement la position d'un objet dans l'espace. Il s'avère que les coordonnées de l'objet sont déterminées par la matrice tridimensionnelle R et le vecteur tridimensionnel t , c'est-à-dire 12 paramètres. De plus, ces paramètres ne sont pas indépendants les uns des autres, les composants de la matrice de rotation sont interconnectés par certaines conditions. Par conséquent, du point de vue de l'utilisation de ces fonctions dans l'optimisation, ces paramètres ne sont pas la meilleure solution. Il y a plus de paramètres que de degrés de liberté, il y a une relation entre eux. Il existe une autre forme de rotation - la formule de rotation de Rodrigue . Cette rotation est spécifiée par trois paramètres, formant un vecteur tridimensionnel.

Le vecteur normalisé est l'axe de rotation, et la longueur de ce vecteur est l'angle de rotation autour de cet axe.

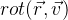
Nous définissons la fonction de rotation du vecteur v : en utilisant les paramètres r de la formule Rodrigue. Nous obtenons la formule suivante à partir de cela: .
Et à la fin, nous pouvons définir les coordonnées de la position de l'objet avec un vecteur à 6 dimensions:
Nous obtenons la formule suivante: .

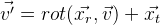
Modèle de caméra sténopé

Nous décrivons maintenant un modèle mathématique simple de la caméra utilisée dans le projet:

$$

$$\ vec {p} = \ begin {pmatrix} p_x & p_y \ end {pmatrix} ^ T = cam (\ vec {v}) = \ begin {pmatrix} f_x \ frac {v_x} {v_z} + c_x & f_y \ frac {v_y} {v_z} + c_y \ end {pmatrix} ^ T$$

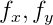
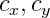
où - distance focale en pixels; - Le centre optique est également en pixels. Ce sont des paramètres de caméra individuels, appelés paramètres intrinsèques de la caméra. Typiquement, ces paramètres sont connus à l'avance. Dans ce projet, ces paramètres sont sélectionnés à l'œil nu.

Ce modèle ne prend pas en compte la distorsion de l'objectif des caméras ( distorsion ). Supposons qu'ils ne le soient pas.

Avec ce modèle, nous obtenons une projection centrale, dont tous les points tendent plus vers le centre optique, plus ils sont éloignés de la caméra. On obtient ainsi l'effet d'un chemin de fer rétrécissant:



Dans l'espace, la caméra est alignée sur l'axe z , le plan image est parallèle au plan xy . Nous complétons notre modèle avec la capacité de se déplacer dans l'espace:

$$

$$\ vec {p} _j = cam (rot (\ vec {x} _r, \ vec {v} _j) + \ vec {x} _t)$$

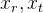
Ainsi, nous avons obtenu un modèle avec lequel nous pouvons simuler sous forme algébrique la projection de points du monde extérieur sur l'image de la caméra (des coordonnées du monde à l'écran). Pour nous, les paramètres de la position relative de la caméra dans l'espace restent inconnus dans ce modèle. . Ces paramètres sont appelés paramètres extrinsèques de la caméra.

Suivi

Déjà implémenté sans outils OpenCV. Tout d'abord, nous devons obtenir la fonction d'erreur pour notre solution approximative, qui a été décrite ci-dessus. Et nous écrirons son calcul par étapes:

1. Nous sélectionnons les bords du modèle de suivi qui sont visibles en fonction des paramètres de l'approximation actuelle.
2. Nous transformons l'ensemble d'arêtes sélectionné en un ensemble fixe de points, pour simplifier les calculs. Il est possible, par exemple, de prendre le nième nombre de points de chaque bord, ou (une option plus correcte) de choisir une telle quantité pour qu'il y ait une distance fixe en pixels entre les points. Nous les appellerons points de contrôle (dans le projet: controlPoint - points de contrôle et controlPixelDistance - la même distance fixe en pixels).
3. Nous projetons des points de contrôle sur l'image. Grâce à distanceImage, nous pouvons obtenir la distance de la projection du point de contrôle au bord de l'image. Dans le cas idéal, tous les points de contrôle doivent reposer strictement sur les bords de l'image, c'est-à-dire la distance à la côte doit être nulle. Sur cette base, nous obtenons une erreur pour un point de contrôle spécifique: .
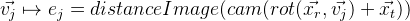4. Nous obtenons la fonction d'erreur suivante:

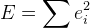
Reste maintenant à trouver un minimum de E. Pour ce faire, nous utilisons l'algorithme de Levenberg-Marquardt décrit ci-dessus. Comme nous le savons déjà, l'algorithme nécessite le calcul de la matrice de Jacobi, c'est-à-dire fonctions dérivées. Vous pouvez utiliser la recherche numérique des dérivés. Vous pouvez également utiliser des solutions prêtes à l'emploi pour cet algorithme. Cependant, dans ce projet, tout a été écrit manuellement, donc je vais décrire la conclusion complète de la solution entière.

Pour chaque point de contrôle, nous obtenons une équation indépendante des autres points. Il a déjà été décrit ci-dessus que dans ce cas, il est possible de considérer ces équations indépendamment les unes des autres, en calculant la matrice de Jacobi spécifiquement pour chacune. Nous allons l'analyser dans l'ordre, en utilisant les règles de différenciation d'une fonction complexe:



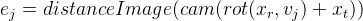
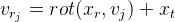
Nous dénotons alors



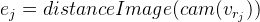
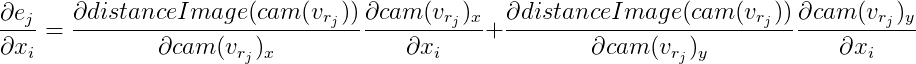
D'ici:



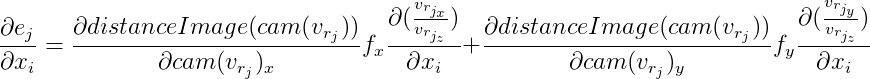
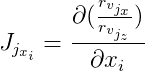
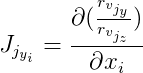
De plus, nous désignons et puis:


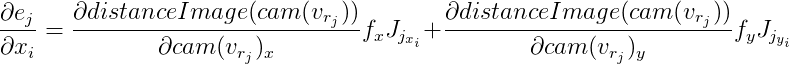
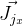
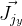
Les dérivées de distanceImage sont numériques. Et pour calculer des vecteurs et vous devrez trouver des dérivés selon la formule de rotation de Rodrigue. J'ai trouvé jacobien par cette formule dans la publication «Une formule compacte pour la dérivée d'une rotation 3D dans
coordonnées exponentielles »Guillermo Gallego, Anthony Yezzi :

,
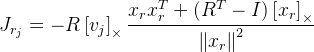
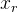
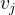
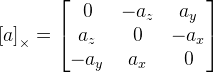
où R est la matrice de rotation obtenue par la formule de Rodrigue à partir du vecteur de rotation ; - le point sur lequel nous tournons; I est la matrice d'identité; . Comme nous le voyons ici, nous avons une division par la longueur du vecteur de rotation, et si le vecteur est nul, alors la formule ne fonctionne plus. Cela est probablement dû au fait qu'au niveau du vecteur zéro, l'axe de rotation n'est pas défini. Si le vecteur de rotation est très proche de zéro, alors nous utilisons cette formule: .
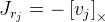
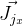
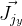
Reste à peindre et (ici l'index j est omis):


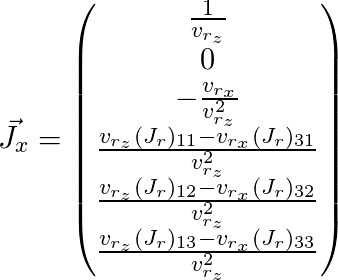
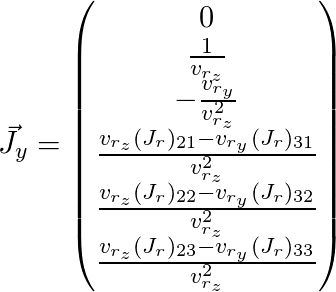
Ainsi, nous avons obtenu la matrice de Jacobi pour le point dont nous avons besoin et pouvons l'utiliser pour l'algorithme d'optimisation décrit ci-dessus.

Il y a plusieurs problèmes avec cet algorithme. Tout d'abord, la précision. En conséquence, la position globale de la caméra saute légèrement d'une image à l'autre. Vous pouvez le réparer un peu. Nous avons a priori des informations selon lesquelles la position de la caméra ne peut pas changer radicalement d'une image à l'autre. Et nous pouvons réduire cette gigue en ajoutant des équations supplémentaires à la fonction.

Il faut rappeler que le vecteur de déplacement t n'est pas dans notre cas la coordonnée de la position globale de la caméra. La position globale est un point local avec des coordonnées nulles, il peut donc être dérivé comme suit:



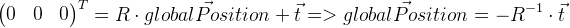
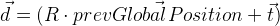
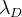
Nous nous souvenons de la position de l'image précédente dans prevGlobalPosition . Maintenant, la position précédente devrait être proche de zéro, c'est-à-dire longueur du vecteur devrait être assez petit. C'est-à-dire outre les autres valeurs de divergences, le vecteur d doit également être minimisé. Pour déterminer le degré d'influence de cette modification, nous introduisons la valeur et multiplier le vecteur d en ajoutant par : . 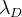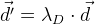C'est-à-dire dans l'algorithme d'optimisation, nous minimisons en outre le vecteur d ' . Bien sûr, pour cela, il sera nécessaire de calculer la matrice de Jacobi, qui est dérivée de la même manière que nous avons déjà dérivé ci-dessus pour la fonction d'erreur générale.

Le deuxième problème de l'algorithme est qu'il peut rester bloqué dans les minima locaux. Dans d'autres travaux, ce problème est résolu en utilisant un filtre à particules. Dans notre cas, cette option s'est avérée, en principe, suffisante.

Bonus de suivi d'un objet

Connaissant la position et la forme de l'objet, vous pouvez les manipuler visuellement, ce que j'ai essayé de démontrer sur la vidéo. L'objet a été déformé à l'aide de shaders OpenGL. A l'aide de notre modèle, j'ai projeté le point de l'objet sur l'image, et ainsi reçu la couleur de ce point. Ensuite, vous pouvez déplacer ce point, obtenant des effets intéressants - par exemple, le morphing. Cependant, il faut se rappeler qu'en déplaçant le point, il faut que quelque chose reste à sa place, sinon des incohérences deviendront perceptibles. En outre, en fonction de la qualité de notre suivi et de la forme de l'objet, nous recevrons divers effets indésirables dus aux erreurs accumulées, qui le seront toujours. Il faut juste en tenir compte d'une manière ou d'une autre. Dans la vidéo présentée ci-dessus, je voulais montrer que la réalité augmentée peut être utilisée un peu plus large que d'imposer simplement des objets virtuels à l'image.

Soit dit en passant, le SDK Vuforia implémente le suivi d'un objet par sa forme, bien que je ne pense pas qu'il serait possible de mettre en œuvre ce projet avec lui, car il n'est pas possible d'utiliser des bords strictement définis et ne peut pas être associé à l'éclairage du bâtiment.