Un article de l'équipe Stitch Fix suggère d'utiliser une approche de recherche clinique sur les essais de non-infériorité dans le marketing et les tests A / B des produits. Cette approche est vraiment applicable lorsque nous testons une nouvelle solution qui présente des avantages qui ne sont pas mesurables par des tests.
L'exemple le plus simple est la perte osseuse. Par exemple, nous automatisons le processus d'attribution de la première leçon, mais nous ne voulons pas trop abandonner la conversion. Ou nous testons des changements qui sont concentrés sur un segment d'utilisateurs, tout en nous assurant que les conversions sur d'autres segments ne coulent pas beaucoup (lors du test de plusieurs hypothèses, n'oubliez pas les corrections).
Le choix de la bonne bordure non moins efficace ajoute des difficultés supplémentaires au stade de la conception du test. La question de savoir comment choisir Δ dans l'article n'est pas bien divulguée. Il semble que ce choix ne soit pas totalement transparent dans les essais cliniques.
Un examen des publications médicales sur la non-infériorité révèle que dans seulement la moitié des publications, le choix de la frontière est justifié et souvent ces justifications sont ambiguës ou non détaillées.
En tout cas, cette approche semble intéressante, car en réduisant la taille d'échantillon requise, il peut augmenter la vitesse des tests et, par conséquent, la vitesse de prise de décision. -
Daria Mukhina, analyste produit pour l'application mobile Skyeng.L'équipe Stitch Fix aime tester différentes choses. Toute la communauté technologique, en principe, aime effectuer des tests. Quelle version du site attire plus d'utilisateurs - A ou B? La version A du modèle de recommandation rapporte-t-elle plus d'argent que la version B? Presque toujours, pour tester des hypothèses, nous utilisons l'approche la plus simple d'un cours de statistiques de base:
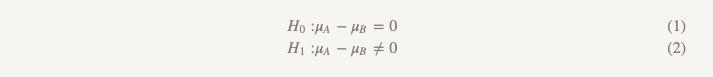
Bien que nous utilisions rarement ce terme, cette forme de test est appelée «hypothèse du test de supériorité». Avec cette approche, nous supposons qu'il n'y a pas de différence entre les deux options. Nous adhérons à cette idée et la refusons uniquement si les données obtenues sont suffisamment convaincantes pour cela - c'est-à-dire qu'elles démontrent que l'une des options (A ou B) est meilleure que l'autre.
Le test de l'hypothèse de supériorité convient pour résoudre de nombreux problèmes. Nous ne publions la version B du modèle de recommandation que si elle est évidemment meilleure que la version A déjà utilisée. Mais dans certains cas, cette approche ne fonctionne pas aussi bien. Regardons quelques exemples.
1) Nous utilisons un service tiers qui aide à identifier les fausses cartes bancaires. Nous avons trouvé un autre service qui coûte beaucoup moins cher. Si un service moins cher fonctionne aussi bien que celui que nous utilisons actuellement, nous le choisirons. Il ne doit pas nécessairement être meilleur que le service utilisé.
2) Nous voulons abandonner la source de données A et la remplacer par la source de données B. Nous pouvons retarder l'abandon de A si B produit de très mauvais résultats, mais il n'est pas possible de continuer à utiliser A.
3) Nous aimerions passer de l'approche à la modélisation A à l'approche B non pas parce que nous attendons de meilleurs résultats de B, mais parce que cela nous donne une grande flexibilité opérationnelle. Nous n'avons aucune raison de croire que B sera pire, mais nous n'entamerons pas la transition si tel est le cas.
4) Nous avons apporté plusieurs modifications qualitatives à la conception du site Web (version B) et nous pensons que cette version est supérieure à la version A. Nous ne nous attendons pas à des changements dans la conversion ou à tout indicateur de performance clé par lequel nous évaluons généralement le site Web. Mais nous pensons qu'il y a des avantages dans les paramètres qui sont soit incommensurables, soit nos technologies ne sont pas suffisantes pour mesurer.
Dans tous ces cas, la recherche de l'excellence n'est pas la meilleure solution. Mais la plupart des experts dans ces situations l'utilisent par défaut. Nous menons soigneusement une expérience pour déterminer correctement l'ampleur de l'effet. S'il était vrai que les versions A et B fonctionnent de manière très similaire, il est possible que nous ne puissions pas rejeter l'hypothèse nulle. En concluons-nous que A et B fonctionnent généralement de la même manière? Non! L'incapacité de rejeter l'hypothèse nulle et l'adoption de l'hypothèse nulle ne sont pas la même chose.
Les calculs de la taille de l'échantillon (que vous avez bien sûr effectué) sont généralement effectués avec des limites plus strictes pour la première erreur de type (probabilité de rejet erroné de l'hypothèse nulle, souvent appelée alpha) que pour la seconde erreur de type (probabilité d'échec de rejet de l'hypothèse nulle, lorsque en supposant que l'hypothèse nulle est fausse, souvent appelée bêta). La valeur typique pour alpha est 0,05, tandis que la valeur typique pour beta est 0,20, ce qui correspond à une puissance statistique de 0,80. Cela signifie qu'avec nous, nous ne pouvons pas détecter la véritable influence de la valeur que nous avons indiquée dans nos calculs de puissance avec une probabilité de 20% et il s'agit d'un manque d'informations assez sérieux. À titre d'exemple, considérons les hypothèses suivantes:
H0: mon sac à dos n'est PAS dans ma chambre (3)
H1: mon sac à dos est dans ma chambre (4)Si j'ai fouillé ma chambre et trouvé mon sac à dos - très bien, je peux refuser l'hypothèse nulle. Mais si je regardais autour de la pièce et ne pouvais pas trouver mon sac à dos (figure 1), quelle conclusion devrais-je tirer? Suis-je sûr qu'il n'est pas là? Ai-je suffisamment cherché? Et si je cherchais seulement 80% de la pièce? Conclure que le sac à dos n'est certainement pas dans la pièce sera une décision irréfléchie. Sans surprise, nous ne pouvons pas "accepter l'hypothèse nulle".
La zone que nous avons recherchée
Nous n'avons pas trouvé de sac à dos - devons-nous accepter l'hypothèse nulle?Figure 1. La recherche dans 80% de la pièce équivaut à peu près à la réalisation d'une étude d'une capacité de 80%. Si vous n'avez pas trouvé de sac à dos, après avoir examiné 80% de la pièce, est-il possible de conclure qu'il n'est pas là?Alors, que fait un spécialiste des données dans cette situation? Vous pouvez augmenter considérablement la puissance de recherche, mais vous aurez alors besoin d'un échantillon beaucoup plus grand et le résultat ne sera toujours pas satisfaisant.
Heureusement, de tels problèmes sont étudiés depuis longtemps dans le monde de la recherche clinique. Le médicament B est moins cher que le médicament A; le médicament B devrait provoquer moins d'effets secondaires que le médicament A; le médicament B est plus facile à transporter car il n'a pas besoin d'être conservé au réfrigérateur et le médicament A est nécessaire. Nous testons l'hypothèse de non moins d'efficacité. Cela est nécessaire pour montrer que la version B est aussi bonne que la version A - au moins dans une certaine limite prédéterminée de «pas moins d'efficacité», Δ. Un peu plus tard, nous parlerons davantage de la façon de définir cette limite. Mais supposons maintenant qu'il s'agit de la plus petite différence qui soit pratiquement significative (dans le contexte des essais cliniques, cela est généralement appelé pertinence clinique).
Des hypothèses non moins efficaces bouleversent tout:
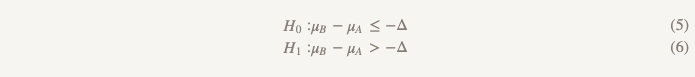
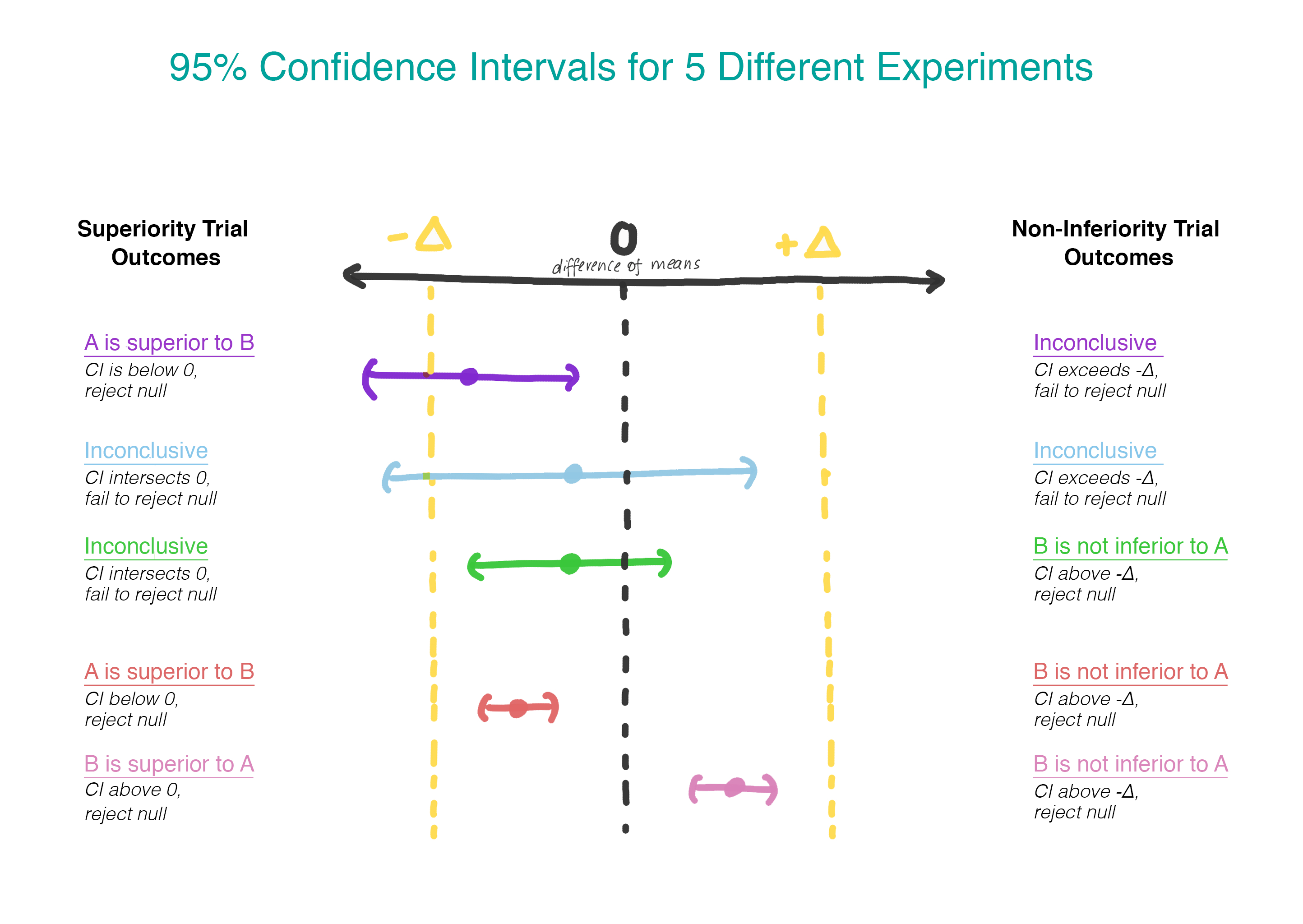
Maintenant, au lieu de supposer qu'il n'y a pas de différence, nous supposons que la version B est pire que la version A, et nous nous en tiendrons à cette hypothèse jusqu'à ce que nous démontrions qu'elle ne l'est pas. C'est exactement le moment où il est logique d'utiliser le test d'une hypothèse unilatérale! En pratique, cela peut être fait en construisant un intervalle de confiance et en déterminant si l'intervalle est vraiment supérieur à Δ (figure 2).
Δ sélection
Comment choisir Δ? Le processus de sélection Δ comprend une justification statistique et une évaluation du sujet. Il existe des recommandations normatives dans le monde des essais cliniques, d'où il résulte que le delta devrait être la plus petite différence cliniquement significative - celle qui sera pertinente dans la pratique. Voici une citation du leadership européen, avec laquelle vous pouvez vérifier vous-même: «Si la différence a été choisie correctement, un intervalle de confiance qui se situe complètement entre –∆ et 0 ... est encore suffisant pour démontrer non moins d'efficacité. Si ce résultat ne semble pas acceptable, cela signifie que ∆ n'a pas été choisi de manière appropriée. »
Le delta ne doit certainement pas dépasser l'ampleur de l'effet de la version A par rapport au vrai contrôle (placebo / absence de traitement), car cela nous amène à penser que la version B est pire que le vrai contrôle, et démontre en même temps «pas moins d'efficacité». Supposons que lorsque la version A a été introduite, la version 0 était à sa place ou la fonction n'existait pas du tout (voir figure 3).
Sur la base des résultats du test de l'hypothèse de supériorité, l'ampleur de l'effet E a été révélée (c'est-à-dire, vraisemblablement μ ^ A - μ ^ 0 = E). Maintenant, A est notre nouveau standard, et nous voulons nous assurer que B n'est pas inférieur à A. Une autre façon d'écrire μB - μA≤ - Δ (hypothèse nulle) est μB≤μA - Δ. Si nous supposons que faire est égal ou supérieur à E, alors μB ≤ μA - E ≤ placebo. Nous voyons maintenant que notre estimation pour μB dépasse complètement μA - E, ce qui réfute ainsi complètement l'hypothèse nulle et nous permet de conclure que B n'est pas inférieur à A, mais en même temps, μB peut être ≤ μ placebo, mais ce n'est pas le cas de quoi avons-nous besoin. (figure 3).
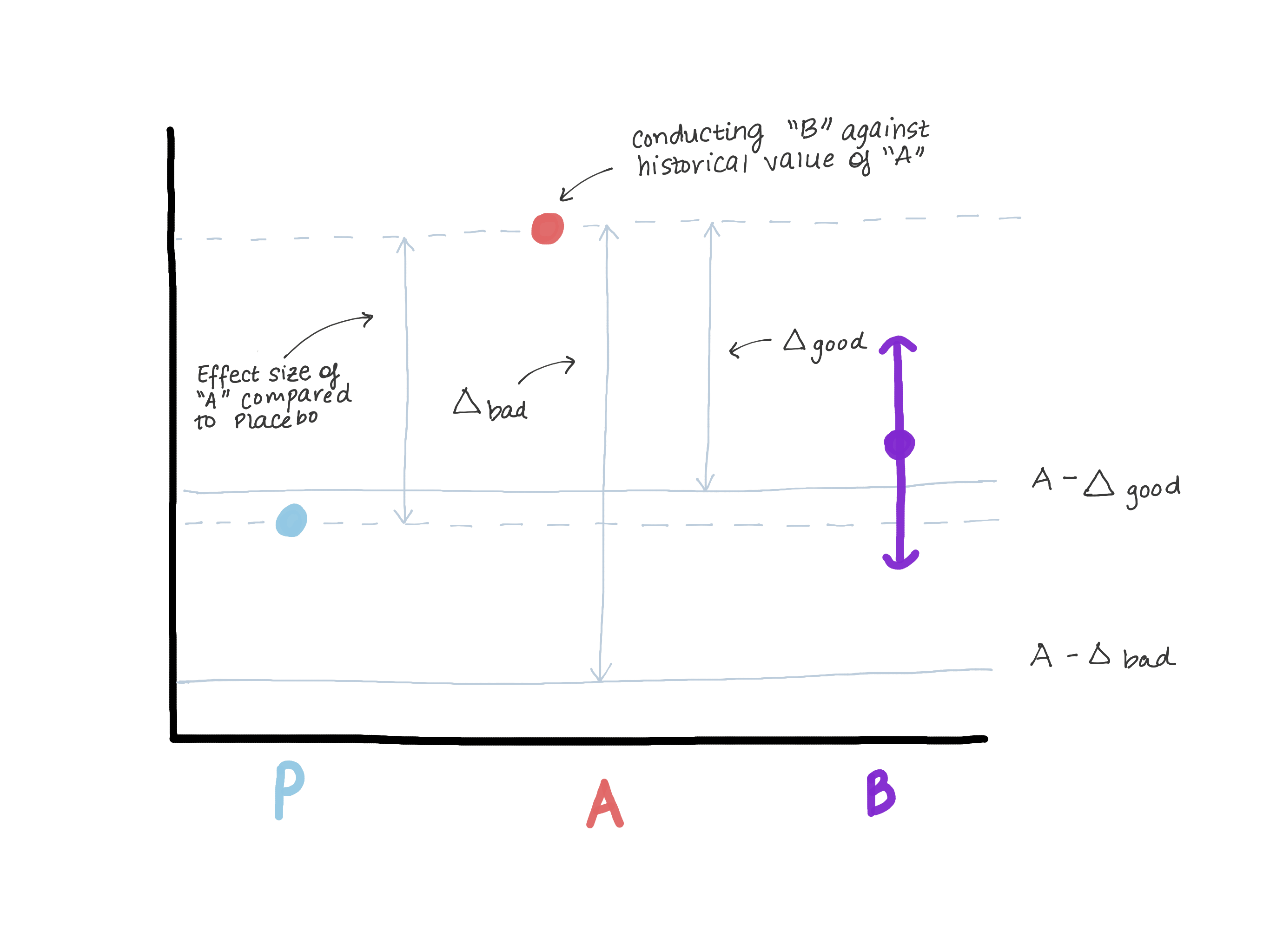Figure 3. Démonstration des risques de choisir une frontière non moins efficace. Si la limite est trop grande, nous pouvons conclure que B n'est pas inférieur à A, mais en même temps indiscernable du placebo. Nous ne changerons pas le médicament, qui est clairement plus efficace que le placebo (A), sur le médicament, qui a la même efficacité que le placebo.Choisir α
On passe au choix de α. Vous pouvez utiliser la valeur standard α = 0,05, mais ce n'est pas tout à fait honnête. Comme, par exemple, lorsque vous achetez quelque chose sur Internet et utilisez plusieurs codes de réduction à la fois, bien qu'ils ne devraient pas être résumés, le développeur a simplement fait une erreur et vous vous en êtes tiré. Selon les règles, la valeur de α doit être égale à la moitié de la valeur de α, qui est utilisée pour tester l'hypothèse de supériorité, c'est-à-dire 0,05 / 2 = 0,025.
Taille d'échantillon
Comment estimer la taille de l'échantillon? Si vous pensez que la vraie différence moyenne entre A et B est 0, alors le calcul de la taille de l'échantillon sera le même que lors du test de l'hypothèse de supériorité, sauf que vous remplacez la taille de l'effet par une limite d'au moins efficacité, à condition que vous utiliser
α pas moins d'efficacité = 1/2 supériorité (α non-infériorité = 1/2 supérieure). Si vous avez des raisons de croire que l'option B peut être légèrement pire que l'option A, mais que vous voulez prouver qu'elle n'est pire que de Δ, alors vous avez de la chance! En fait, cela réduit la taille de votre échantillon, car il est plus facile de démontrer que B est pire que A si vous pensez vraiment qu'il est légèrement pire et non équivalent.
Exemple de solution
Supposons que vous souhaitiez passer à la version B à condition qu'elle soit pire que la version A de pas plus de 0,1 point sur une échelle de satisfaction client de 5 points ... Nous aborderons cette tâche en utilisant l'hypothèse de supériorité.
Pour tester l'hypothèse de supériorité, nous calculerions la taille de l'échantillon comme suit:
Autrement dit, si vous avez 2103 observations dans votre groupe, vous pouvez être sûr à 90% que vous trouverez un effet de 0,10 ou plus. Mais si la valeur de 0,10 est trop grande pour vous, vous ne devriez peut-être pas tester l'hypothèse de supériorité pour cela. Peut-être, pour la fiabilité, vous décidez de mener une étude pour une taille d'effet plus petite, par exemple 0,05. Dans ce cas, vous aurez besoin de 8407 observations, c'est-à-dire que l'échantillon augmentera presque 4 fois. Mais que se passe-t-il si nous nous en tenons à la taille de notre échantillon d'origine, mais augmentons la puissance à 0,99 afin de ne pas douter si nous obtenons un résultat positif? Dans ce cas, n pour un groupe sera 3676, ce qui est mieux, mais augmente la taille de l'échantillon de plus de 50%. Et par conséquent, nous ne pouvons tout simplement pas réfuter l'hypothèse nulle et n'obtenons pas la réponse à notre question.
Et si, au contraire, nous testions l'hypothèse d'une efficacité non moindre?
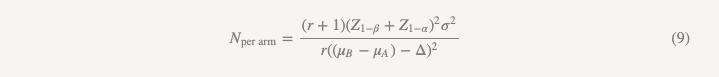
La taille de l'échantillon sera calculée à l'aide de la même formule à l'exception du dénominateur.
Les différences par rapport à la formule utilisée pour tester l'hypothèse de supériorité sont les suivantes:
- Z1 - α / 2 est remplacé par Z1 - α, mais si vous faites tout selon les règles, vous remplacez α = 0,05 par α = 0,025, c'est-à-dire que c'est le même nombre (1,96)
- apparaît dans le dénominateur (μB - μA)
- θ (amplitude de l'effet) est remplacé par Δ (limite de non moins efficacité)
Si nous supposons que µB = µA, alors (µB - µA) = 0 et calculer la taille de l'échantillon pour une limite de non moins d'efficacité est exactement ce que nous obtiendrions en calculant la supériorité pour la valeur d'effet de 0,1, tant mieux! Nous pouvons mener une étude de la même échelle avec des hypothèses différentes et une approche différente des conclusions, et nous obtiendrons une réponse à la question à laquelle nous voulons vraiment répondre.
Supposons maintenant que nous ne pensons pas vraiment que µB = µA et
nous pensons que µB est un peu pire, peut-être 0,01 unités. Cela augmente notre dénominateur, réduisant la taille de l'échantillon par groupe à 1737.
Que se passe-t-il si la version B est réellement meilleure que la version A? Nous réfutons l'hypothèse nulle selon laquelle B est pire que A de plus de Δ et acceptons l'hypothèse alternative selon laquelle B, si elle est pire, n'est pas pire que Δ, et pourrait être meilleure. Essayez de mettre cette conclusion dans une présentation interfonctionnelle et voyez ce qui en résulte (sérieusement, essayez-le). Dans une situation où vous devez vous concentrer sur l'avenir, personne ne veut accepter «pire que Δ et peut-être mieux».
Dans ce cas, nous pouvons mener une étude, qui est appelée très brièvement "tester l'hypothèse selon laquelle l'une des options est supérieure à l'autre ou inférieure à elle". Il utilise deux ensembles d'hypothèses:
Le premier ensemble (le même que lors du test de l'hypothèse de non moins d'efficacité):
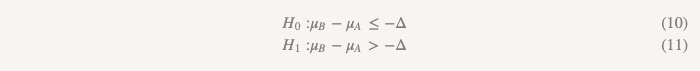
Le deuxième ensemble (le même que lors du test de l'hypothèse de supériorité):
Nous testons la deuxième hypothèse uniquement si la première est rejetée. Dans les tests séquentiels, nous maintenons le niveau global d'erreurs du premier type (α). En pratique, cela peut être réalisé en créant un intervalle de confiance à 95% pour la différence entre les moyennes et en vérifiant si tout l'intervalle dépasse -Δ. Si l'intervalle ne dépasse pas -Δ, nous ne pouvons pas rejeter la valeur zéro et arrêter. Si l'intervalle entier dépasse vraiment −Δ, nous continuons et voyons si l'intervalle contient 0.
Il existe un autre type de recherche dont nous n'avons pas discuté - les études d'équivalence.
Les études de ce type peuvent être remplacées par des études pour tester l'hypothèse d'une efficacité non moindre et vice versa, mais en fait elles ont une différence importante. Un test pour tester l'hypothèse d'une efficacité non moindre vise à montrer que l'option B est au moins aussi bonne que A. Et une étude d'équivalence vise à montrer que l'option B est au moins aussi bonne que A, et l'option A est aussi bonne que B, ce qui est plus compliqué. Essentiellement, nous essayons de déterminer si tout l'intervalle de confiance se situe pour la différence de moyennes entre −Δ et Δ. De telles études nécessitent un plus grand échantillon et sont moins fréquentes. Par conséquent, la prochaine fois que vous effectuerez une étude dans laquelle votre tâche principale est de vous assurer que la nouvelle version n'est pas pire, ne vous contentez pas de "l'incapacité de réfuter l'hypothèse nulle". Si vous voulez tester une hypothèse vraiment importante., Considérez diverses options.