
Salut, habrozhiteli! Marcos Lopez de Prado partage ce qu'ils cachent habituellement - les algorithmes d'apprentissage automatique les plus rentables qu'il utilise depuis deux décennies pour gérer d'importants pools de fonds des investisseurs les plus exigeants.
L'apprentissage automatique modifie presque tous les aspects de notre vie; les algorithmes MO effectuent des tâches qui, jusqu'à récemment, n'étaient approuvées que par des experts de confiance. Dans un avenir proche, le machine learning dominera la finance, la diseuse de bonne aventure appartiendra au passé et les investissements ne seront plus synonymes de jeu.
Profitez-en pour participer à la «révolution de la machine», pour cela il suffit de se familiariser avec le premier livre, qui propose une analyse complète et systématique des méthodes de machine learning en relation avec la finance: en commençant par les structures de données financières, en marquant les séries financières, en pesant l'échantillon, en différenciant les séries temporelles ... et en terminant par toute la partie dédiée au backtesting correct des stratégies d'investissement.
Extrait. Comprendre les stratégies de risque
15.1. Pertinence
Les stratégies d'investissement sont souvent mises en œuvre en termes de positions détenues jusqu'à ce que l'une des deux conditions soit remplie: 1) la condition pour quitter la position avec des bénéfices (prendre des bénéfices) ou 2) la condition pour quitter la position avec des pertes (arrêter la perte). Même lorsque la stratégie ne déclare pas explicitement un arrêt de perte, il existe toujours une limite d'arrêt de perte implicite à laquelle l'investisseur ne peut plus financer sa position (appel de marge) ou encourt des dommages causés par une augmentation de la perte non réalisée. Étant donné que la plupart des stratégies ont (explicitement ou implicitement) ces deux conditions de sortie, il est logique de modéliser la distribution des résultats à travers un processus binomial. Ceci, à son tour, nous aidera à comprendre quelles combinaisons de taux de paris, de risques et de paiements ne sont pas économiques. Le but de ce chapitre est de vous aider à évaluer quand une stratégie est vulnérable à de petits changements dans l'une de ces quantités.
Considérons une stratégie qui produit annuellement n paris identiques et indépendants les uns des autres, où le résultat Xi du pari i ∈ [1, n] est le profit π> 0 avec la probabilité P [Xi = π] = p et la perte –π avec la probabilité P [Xi = –Π] = 1 - p. Vous pouvez imaginer p comme la précision d'un classificateur binaire, dans lequel un résultat affirmatif signifie parier sur une opportunité, et un résultat négatif signifie une opportunité manquante: les vraies déclarations sont récompensées, les fausses déclarations sont punies et les résultats négatifs (qu'ils soient vrais ou faux) n'ont aucun gain. Puisque les résultats des paris {Xi} i = 1, ..., n sont indépendants, nous calculerons les moments attendus par pari. Le bénéfice attendu d'un pari est E [Xi] = πp + (–π) (1 - p) = π (2p - 1). La variance est
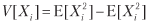
où
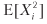
= π2p + (–π) 2 (1 - p) = π2, donc V [Xi] = π2 - π2 (2p - 1) 2 = π2 [1– (2p - 1) 2] = 4π2p (1 - p ) Pour n taux annuels distribués de façon identique et indépendants les uns des autres, le rapport annuel moyen de Sharpe (θ) est
Remarquez comment π équilibre l'équation ci-dessus car les paiements sont symétriques. Comme dans le cas gaussien, θ [p, n] peut être compris comme une valeur t redimensionnée1. Cela illustre le fait que même pour les petites
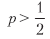
le rapport de Sharpe peut être élevé pour un n suffisamment grand. Cela sert de base économique pour le trading à haute fréquence, où p peut être légèrement supérieur à 0,5, et la clé d'une activité de change réussie est une augmentation de n. Le ratio de Sharpe est fonction de la précision et non de la justesse, car rater une opportunité (déclaration négative) n'est pas récompensé ou puni directement (bien que trop de déclarations négatives puissent conduire à un petit n, ce qui réduira le coefficient de Sharpe à zéro).
Par exemple, pour
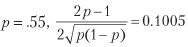
et pour atteindre un ratio Sharpe annuel moyen de 2 396 paris par an sont nécessaires. Le listing 15.1 vérifie ce résultat expérimentalement. La figure 15.1 montre le ratio de Sharpe en fonction de la précision pour différentes fréquences de mise.
Listing 15.1. Ratio de Sharpe en fonction du nombre de paris
out,p=[],.55 for i in xrange(1000000): rnd=np.random.binomial(n=1,p=p) x=(1 if rnd==1 else -1) out.append(x) print np.mean(out),np.std(out),np.mean(out)/np.std(out)
Cette équation exprime assez clairement le compromis entre précision (p) et fréquence (n) pour un coefficient de Sharpe donné (θ). Par exemple, afin de donner un ratio de Sharpe annuel moyen de 2 pour une stratégie qui ne produit que des taux hebdomadaires (n = 52), une précision assez élevée p = 0,6336 sera nécessaire.
15.3. Paiements asymétriques
Considérons une stratégie qui produit n paris mutuellement indépendants et identiques chaque année, où le résultat Xi du pari i ∈ [1, n] est π + avec la probabilité P [Xi = π +] = p, et le résultat π– (π– <π + ) se produit avec une probabilité P [Xi = π_] = 1 - p. Le bénéfice attendu d'un pari est E [Xi] = pπ + + (1 - p) π– = (π + - π–) p + π–. La dispersion est V [Xi] =, où
Enfin, nous pouvons résoudre l'équation précédente pour 0 ≤ p ≤ 1 et obtenir
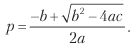
où:
a = (n + θ2) (π + - π–) 2;
b = [2nπ - θ2 (π + - π -)] (π + - π–);

Remarque: Le listing 15.2 vérifie ces opérations symboliques à l'aide du shell Python SymPy Live exécuté sur le service cloud de Google App Engine:
live.sympy.org .
Listing 15.2. Utilisation de la bibliothèque SymPy pour les opérations symboliques
>>> from sympy import * >>> init_printing(use_unicode=False,wrap_line=False,no_global=True) >>> p,u,d=symbols('pu d') >>> m2=p*u**2+(1-p)*d**2 >>> m1=p*u+(1-p)*d >>> v=m2-m1**2 >>> factor(v)
L'équation ci-dessus répond à la question suivante: pour une règle de trading donnée caractérisée par les paramètres {π–, π +, n}, quel est le degré de précision p nécessaire pour atteindre le ratio de Sharpe égal à θ *? Par exemple, pour obtenir θ = 2 pour n = 260, π– = –.01, π + = .005, nous avons besoin de p = .72. En raison du grand nombre de paris, un très petit changement de p (de p = 0,7 à p = 0,72) a fait passer le ratio de Sharpe de θ = 1,173 à θ = 2. D'autre part, cela nous indique également que cette stratégie est vulnérable aux petits changements dans p. Le listing 15.3 implémente la dérivation de la précision attendue. Dans la fig. 15.2 montre la précision supposée en fonction de n et π–, où π + = 0,1 et θ * = 1,5. Lorsque le seuil π– devient plus négatif pour un n donné, un degré p plus élevé est nécessaire pour atteindre θ * pour un seuil π + donné. Comme le nombre n devient plus petit pour un seuil donné π–, un degré plus élevé de p est nécessaire pour atteindre θ * pour un π + donné.
Listing 15.3. Calcul de la précision estimée
def binHR(sl,pt,freq,tSR): ´´´
Pour une règle de négociation donnée caractérisée par les paramètres {sl, pt, freq}, quelle est la précision minimale requise pour atteindre le ratio de Sharpe égal à tSR?
1) Entrées
sl: seuil d'arrêt de perte
pt: seuil de profit
freq: le nombre de paris par an
tSR: ratio de Sharpe moyen annuel cible
2) Quitter
p: précision minimale p requise pour atteindre le tSR
´´´
a = (freq + tSR ** 2) * (pt-sl) ** 2
b = (2 * freq * sl-tSR ** 2 * (pt-sl)) * (pt-sl)
c = freq * sl ** 2
p = (- b + (b ** 2-4 * a * c) **. 5) / (2. * a)
retour p
Le listing 15.4 résout θ [p, n, π–, π +] pour la fréquence de paris estimée n. Dans la fig. 15,3 montre la fréquence estimée en fonction de p et π–, où π + = 0,1 et θ * = 1,5. Lorsque le seuil π– devient plus négatif pour un degré p donné, un nombre plus élevé n est nécessaire pour atteindre θ * pour un seuil π + donné. Comme le degré p devient plus petit pour un seuil donné π–, un nombre plus élevé n est nécessaire pour atteindre θ * pour un seuil donné π +.
Listing 15.4. Calcul de la fréquence de paris estimée
def binFreq(sl,pt,p,tSR): ´´´
Pour une règle de trading donnée, caractérisée par les paramètres {sl, pt, freq}, combien de paris par an sont nécessaires pour atteindre le coefficient Sharp tSR avec un degré de précision p?
Remarque: équation avec des radicaux, vérifiez les solutions étrangères.
1) Entrées
sl: seuil d'arrêt de perte
pt: seuil de profit
p: degré de précision p
tSR: ratio de Sharpe moyen annuel cible
2) Quitter
freq: le nombre de paris nécessaires par an
´´´
freq = (tSR * (pt-sl)) ** 2 * p * (1-p) / ((pt-sl) * p + sl) ** 2 # éventuellement étranger
sinon np.isclose (binSR (sl, pt, freq, p), tSR): retour
return freq
»Plus d'informations sur le livre sont disponibles sur
le site Web de l'éditeur»
Contenu»
Extrait25% de réduction sur les colporteurs -
Machine LearningLors du paiement de la version papier du livre, une version électronique du livre est envoyée par e-mail.