Comparaison des algorithmes de tri des échanges

Cet article présente diverses options de tri des échanges et décrit également une application graphique simple ( processing.js ) avec des exemples de tris.

Avant de lire, je vous recommande de lire les articles par utilisateur valemak :

→ Tri des échanges
→ Tri à bulles et tout-tout
→ Tri idiot et quelques autres plus intelligents

Tri des bulles

L'option la plus simple consiste à parcourir le tableau du premier élément au dernier, en échangeant (si nécessaire) les éléments voisins.

→ Vérifiez ici


Pour déplacer le curseur, vous devez cliquer sur le bouton gris dans le coin inférieur gauche.
Lorsque vous cliquez sur le bouton, déplacez le curseur d'un pas vers la droite

slider++; 

Ensuite, nous vérifions: avons-nous atteint la fin du tableau (puis sautons au début), puis comparons (échangeons) les éléments voisins


Processing.js utilise des structures de données Java, puis le code est traduit en javascript ( lien ), donc la déclaration d'un tableau d'instances de la classe Module, qui est responsable du rendu des éléments et de l'initialisation des instances, se produit comme ceci

La fonction principale du dessin void draw () est une boucle infinie dans laquelle les instances de classe sont triées

 for (Module mod : mods) { mod.display(); } 

Ajoutez la fonction randFoo () , qui renvoie des valeurs aléatoires. Pour garantir que les valeurs ne se répètent pas, nous les ajouterons à ArrayLis t dans la liste listRand , et dans la fonction randFoo () , vérifiez si le nouveau nombre aléatoire se trouve dans la liste listRand

 int randFoo(){ newRand = int(random(1,11)); if(!listRand.contains(newRand) ) listRand.add(newRand ); else newRand=randFoo(); return newRand; } 

→ Vérifiez ici

Tri des pixels

Le tri des pixels (ici) est une implémentation du tri des bulles.
Nous déplacerons les pixels les plus chauds / plus clairs d'un côté et les plus sombres / les plus froids de l'autre.

 void draw(){ while (i <= height) { c=get(i,j); //    cTemp=c; //      i++; //     c=get(i,j); //     if(cTemp>c) { //   fill(c); //    rect(i-1,j,1,1); fill(cTemp); rect(i,j,1,1); } } if(mousePressed) { if(j>=width) j=0; } //      if(i >= height) {j++; i=0;} } 

→ Vérifiez ici
Pour commencer le tri, cliquez sur l'image et maintenez le bouton.
Vous pouvez en savoir plus sur les types de pixels ici .
Vidéo sur le tri des pixels sur la chaîne officielle The Coding Train ici

Limiteur et drapeau

Vous pouvez réduire le nombre d'itérations si vous n'effectuez pas d'itération sur des éléments déjà triés. Pour ce faire, ajoutez un limiteur à la fin du tableau, qui se déplacera au début du tableau après chaque itération

 if(slider>=limiter) { slider=1; limiter--; if(limiter<1) limiter=1; } 

→ Vérifiez ici

Une autre façon de réduire le nombre de bustes se trouve dans l'article Bubble Sort (Wikipedia). Si lors du passage du tableau nous n'avons jamais commuté une seule fois les éléments voisins, le tableau est trié et le cycle peut être bouclé (condition Iverson ).

Ajoutez un indicateur de drapeau , qui est levé lorsque nous rencontrons quelques éléments qui doivent être échangés. Si l'indicateur est levé, parcourez à nouveau le tableau. Sinon, mettez fin au cycle. L'état du drapeau est affiché dans la console.



→ Vérifiez ici

Si vous mettez un limiteur à gauche et utilisez un élément avec un limiteur comme référence / minimum, nous obtenons un tri par sélection.

Ajoutez la variable min dans laquelle la valeur minimale sera chargée. Supposons qu'au départ l'élément le plus à gauche soit minimal: lors de la première passe du tableau, si un élément est inférieur au minimum, alors on enregistre cet élément lui-même dans la variable min

 if(mods[slider-1].rectHight < min){ min=mods[slider-1].rectHight; } 

puis échangez le premier élément et le minimum

 if (mods[limiterL-1].rectHight>min) { vTemp= mods[limiterL-1].rectHight; mods[limiterL-1].rectHight=mods[slider-1].rectHight; mods[slider-1].rectHight=vTemp; } 

Si le curseur atteint le bord droit de la matrice, le limiteur se déplace d'un pas vers la droite et le curseur se déplace vers le limiteur

 if(slider==moduleSize){ if(limiterL<moduleSize) limiterL++; min=mods[limiterL-1].rectHight; incPaddle=limiterL-1; } 

→ Vérifiez ici
Le nombre de mesures peut être réduit si, au tout début de la recherche, nous comparons (échangeons) l'élément actuel et l'élément le plus à droite du tableau

 if(mods[limiterL-1].rectHight>mods[moduleSize-1].rectHight) { vTemp=mods[limiterL-1].rectHight; mods[limiterL-1].rectHight=mods[moduleSize-1].rectHight; mods[moduleSize-1].rectHight=vTemp; } 

Ensuite, vous ne pouvez pas vérifier l'élément le plus à droite du tableau

 //if(slider==moduleSize){ if(slider==moduleSize-1){ //if(limiterL<moduleSize) limiterL++; limiterL++; min=mods[limiterL-1].rectHight; slider=limiterL-1; } // slider++; if(slider<moduleSize) slider++; 

→ Vérifiez ici

Ici, vous pouvez ajouter le tri de la partie droite du tableau par ordre décroissant en ajoutant l'élément maximum max - nous obtenons le tri du shaker par sélection. Voir la section sur le tri des shakers à la fin de l'article.

Tri rapide

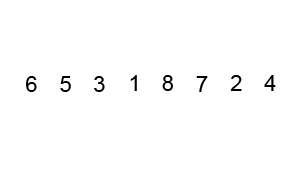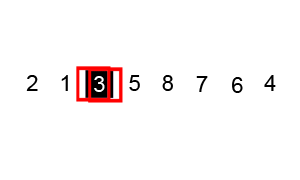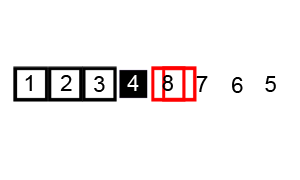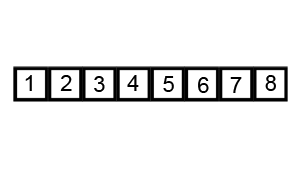
Le mécanisme de sélection des éléments de support est également utilisé dans le tri rapide. Cet algorithme implique la sélection de l'élément de référence initial avec lequel tous les autres éléments du tableau sont comparés. Le temps d'exécution de l'algorithme dépend du choix de l'élément initial. Dans le gif ci-dessus, l'élément de départ est le numéro 3 . Vous pouvez en savoir plus sur le choix de l'élément de support de départ dans l' article (Wikipedia).
Une vidéo sur le tri rapide est disponible sur la chaîne officielle youtube des langages de traitement et p5.js. Ici vous pouvez voir la visualisation de l'algorithme.
Si le premier élément est basique, vous pouvez insérer des éléments plus petits que celui de base en face de lui, puis le tableau sera divisé en deux parties, les éléments de gauche seront plus petits que les éléments de base, à droite - plus. Pour une telle méthode, voir la section sur le tri par insertions ci-dessous.

Tri nain

Essentiellement, le gnome regarde les pots de jardin suivants et précédents: s'ils sont dans le bon ordre, il avance d'un pot, sinon il les échange et recule d'un pot.

Après avoir levé le drapeau, enregistrez les coordonnées du curseur dans le limiteur variable R et remettez le curseur au début du tableau par étapes

 slider--; 

Une fois au début du tableau, réinitialisez le drapeau et placez le curseur dans la cellule avec les coordonnées que nous avons enregistrées dans le limiteur variable

 if(slider==0){ flag=false; slider=limiterR; } 

→ Vérifiez ici

En changeant cet algorithme, nous obtenons le " tri par insertions ".
Dans le tri par insertions, l'élément de référence / minimum est sélectionné, puis dans la partie non triée du tableau, l'élément est sélectionné, plus petit que la référence et inséré avant la référence

Ayons les lieux d'échange d'éléments minimaux avec les précédents, jusqu'à celui de référence, et ainsi de suite. inséré devant la référence.
Ajouter une condition

 if(slider==limiterR-1 && mods[slider-1].rectHight<mods[limiterR-1].rectHight){ flag=false; slider=limiterR; } 

→ Vérifiez ici


Tri par insertion «rapide»

Dans cet algorithme, le tableau est divisé en deux parties par l'élément de support.
Soit le premier élément la référence: comparer, à partir du second, les éléments du tableau avec la référence, si un élément est plus petit que la référence

 if(mods[slider-1].rectHight < mods[pivot-1].rectHight) 

insérer l'élément trouvé avant la référence

 if(mods[slider-1].rectHight < mods[pivot-1].rectHight){ flag=true; //   vTemp= mods[slider-1].rectHight; mods[slider-1].rectHight=mods[slider-2].rectHight; mods[slider-2].rectHight=vTemp; } 

Si le drapeau est levé, déplacez le curseur vers la gauche par étapes jusqu'à ce que nous rencontrions l'élément de support

 if(flag){ slider--; if(slider<pivot){ flag=false; //   pivot++; slider=pivot; } } 

T.O. le tableau est divisé en deux parties, à gauche - les éléments sont plus petits que la référence, à droite - plus

→ Vérifiez ici

Si, après chaque énumération, les coordonnées de l'élément de support sont enregistrées dans ext. tableau pivotsArr , puis lorsque l'élément de référence atteint le bord droit, nous obtenons un tableau trié par niveau / étape. Les éléments de chaque niveau suivant seront plus grands que les éléments du niveau précédent. Les limites des niveaux seront contenues dans add. tableau pivotsArr
Chaque fois que vous cliquez sur le bouton, nous afficherons le tableau pivotsArr sur la console

 for(int i=0;i<pivotsArr.length;i++){ print(" "); print(pivotsArr[i]); print(" "); } 

Ajoutez la fonction aléatoire randFoo () à la fin du programme.

→ Vérifiez ici

Maintenant, vous devez trier les éléments de chaque niveau séparément (il ne reste plus qu'à ajouter la condition pour terminer le cycle)

→ Vérifiez ici
Ce tri peut être décrit comme un tri par niveau.
, car après chaque énumération, les données numériques sont organisées en niveaux, les nombres de chaque niveau suivant dépassent les nombres du précédent.

Tri pair-impair

Nous allons déplacer le curseur de deux étapes, en comparant les éléments voisins

 slider=slider+2; 

T.O. on compare les éléments 0 et 1, 2 et 3, 4 et 5, 6 et 7, etc.
Si le curseur atteint le bord du tableau, laissez le limiteur se déplacer d'un pas vers la gauche et le curseur se déplace au début du tableau.
Ensuite, nous comparons les éléments 1 et 2, 3 et 4, 5 et 6, 7 et 8, etc.
Après avoir atteint le limiteur, nous le décalons d'un pas vers la droite, plaçons le curseur au début du tableau.

→ Vérifiez ici

Trier la brosse à cheveux

Laissez le curseur se trouver au début du tableau et le délimiteur droit à la fin. Comparer (échanger) des éléments. Nous déplaçons le limiteur d'un pas vers la gauche et enregistrons son index dans la variable limiterStore

 if(limiter==moduleSize) { limiter = limiterStore-1; limiterStore = limiter; slider=1; } 

Déplacez le curseur avec l'arrêt à la fin du tableau par étapes

 if(limiter!=moduleSize) { //  limiter     limiter++; slider++; } 

Après avoir atteint la fin de la matrice en tant que limiteur, placez le curseur au début de la matrice et placez le limiteur dans limiterStore-1

 if(limiter==moduleSize) { limiter = limiterStore-1; limiterStore = limiter; slider=1; } 

→ Vérifiez ici

Tri du shaker

Ajoutez le limiteur gauche limitL au début du tableau.
Laissez le drapeau se lever lorsque le curseur atteint le limiteur droit limiteurR, puis le limiteur se déplace d'un pas vers la gauche. De plus, lorsque le drapeau est levé, le curseur se déplace par étapes vers la gauche limiteur limiteur L - le limiteur se déplace d'un pas vers la droite - le curseur se déplace par étapes vers la droite


→ Vérifiez ici

Trieur par choix
Ajoutez au tri des bulles avec le limiteur droit le limiteur gauche. À chaque déplacement du curseur vers la droite, nous vérifions (échange), ce qui est plus grand - l'élément ou le limiteur actuel

 if(mods[slider-1].rectHight<mods[limiterL-1].rectHight){ vTemp= mods[slider-1].rectHight; mods[slider-1].rectHight=mods[limiterL-1].rectHight; mods[limiterL-1].rectHight=vTemp; } 

Lorsque le curseur atteint le limiteur droit limiteur R , le limiteur droit se déplace d'un pas vers la gauche, le limiteur gauche se déplace d'un pas vers la droite, le curseur revient au limiteur gauche

 if(slider>=limiterR){ limiterL++; slider=limiterL; limiterR--; } 

→ Vérifiez ici

PS C'est là qu'une application est décrite qui rend l'étude des algorithmes et des structures de données beaucoup plus intéressante .
Une autre visualisation d'un certain nombre d'algorithmes et de structures de données.
Cet article mentionne un autre site où vous pouvez voir comment les données sont triées par différents algorithmes.
Cet article donne une évaluation de la complexité du tri des bulles.
Plus d'informations sur l'évaluation de la complexité peuvent être lues ici , ici , ici , ici .