
Ceci est un article de traduction de l'atelier de Stanford . Mais devant elle est une petite introduction. Comment se forment les zombies? Tout le monde est tombé dans une situation où vous voulez attirer un ami ou un collègue à votre niveau, mais cela ne fonctionne pas. De plus, "ça ne marche pas" pas tant avec vous qu'avec lui: d'un côté de la balance se trouve un salaire normal, des tâches et ainsi de suite, et de l'autre - la nécessité de réfléchir. La pensée est désagréable et douloureuse. Il abandonne rapidement et continue d'écrire du code, sans inclure le cerveau. Vous imaginez combien d’efforts vous devez dépenser pour surmonter la barrière de l’impuissance apprise, et vous ne le faites tout simplement pas. C'est ainsi que se forment les zombies, qui peuvent apparemment être guéris, mais il semble que personne ne le fera.
Quand j'ai vu que Leslie Lampport (oui, ce même ami des manuels scolaires) venait en Russie et ne faisait pas de rapport, mais une séance de questions-réponses, j'étais un peu prudent. Au cas où, Leslie est un scientifique de renommée mondiale, l'auteur des travaux fondamentaux en informatique distribuée, et vous pouvez également le connaître par les lettres La dans le mot LaTeX - «Lamport TeX». Le deuxième facteur alarmant est sa demande: tous ceux qui viennent devraient (complètement gratuitement) écouter à l'avance quelques-uns de ses rapports, poser au moins une question à leur sujet, et ensuite seulement venir. J'ai décidé de voir ce que Lampport diffusait là-bas - et c'était génial! C'est exactement cette chose, une pilule de lien magique pour traiter un zombie. Je vous préviens: à partir du texte, il peut notamment brûler pour les fans de méthodologies super flexibles et les non-passionnés de tester ce qui est écrit.
Après habrokat, en effet, la traduction du séminaire commence. Bonne lecture!
Quelle que soit la tâche que vous entreprenez, vous devez toujours suivre trois étapes:
- décider quel objectif vous souhaitez atteindre;
- décider comment vous atteindrez votre objectif;
- venez à votre objectif.
Cela vaut également pour la programmation. Lorsque nous écrivons le code, nous avons besoin de:
- décider ce que le programme doit faire;
- déterminer exactement comment il doit remplir sa tâche;
- écrire le code approprié.
La dernière étape, bien sûr, est très importante, mais je n'en parlerai pas aujourd'hui. Au lieu de cela, nous discutons des deux premiers. Chaque programmeur les exécute avant de commencer à travailler. Vous ne vous asseyez pas pour écrire si vous n'avez pas décidé ce que vous écrivez: un navigateur ou une base de données. Une idée précise de l'objectif doit être présente. Et vous êtes sûr de réfléchir à ce que fera exactement le programme, et de ne pas l'écrire d'une manière ou d'une autre dans l'espoir que le code lui-même se transformera en quelque sorte en navigateur.
Comment se déroule exactement cette réflexion préliminaire sur le code? Combien d'efforts devons-nous y consacrer? Tout dépend de la difficulté du problème que nous résolvons. Supposons que nous voulons écrire un système distribué tolérant aux pannes. Dans ce cas, nous devons tout considérer correctement avant de nous asseoir pour le code. Et si nous avons juste besoin d'augmenter la variable entière de 1? À première vue, tout est trivial ici, et aucune réflexion n'est nécessaire, mais nous rappelons ensuite qu'un débordement peut se produire. Par conséquent, même pour comprendre si un problème est simple ou complexe, vous devez d'abord réfléchir.
Si vous réfléchissez à des solutions possibles au problème, vous pouvez éviter les erreurs. Mais cela nécessite que votre pensée soit claire. Pour y parvenir, vous devez noter vos pensées. J'aime beaucoup la citation de Dick Gindon: "Quand vous écrivez, la nature vous montre à quel point votre pensée est bâclée." Si vous n'écrivez pas, il vous semble seulement que vous pensez. Et vous devez noter vos pensées sous forme de spécifications.
Les spécifications remplissent de nombreuses fonctions, en particulier dans les grands projets. Mais je ne parlerai que de l'un d'eux: ils nous aident à penser clairement. Penser clairement est très important et assez difficile, nous avons donc besoin d'aide. Dans quelle langue devrions-nous écrire les spécifications? C'est toujours toujours la première question pour les programmeurs: dans quelle langue nous allons écrire. Il n'y a pas de bonne réponse: les problèmes que nous résolvons sont trop divers. TLA + est utile pour certains - c'est le langage de spécification que j'ai développé. Pour d'autres, il est plus pratique d'utiliser le chinois. Tout dépend de la situation.
Une autre question est plus importante: comment parvenir à une réflexion plus claire? Réponse: nous devons penser comme des scientifiques. C'est une façon de penser qui a fait ses preuves au cours des 500 dernières années. En science, nous construisons des modèles mathématiques de la réalité. L'astronomie fut peut-être la première science au sens strict du terme. Dans le modèle mathématique utilisé en astronomie, les corps célestes apparaissent comme des points de masse, de position et d'élan, bien qu'en réalité ce soient des objets extrêmement complexes avec des montagnes et des océans, des marées. Ce modèle, comme tout autre, est conçu pour résoudre certains problèmes. C'est idéal pour déterminer où diriger le télescope, si vous avez besoin de trouver une planète. Mais si vous voulez prédire la météo sur cette planète, ce modèle ne fonctionnera pas.
Les mathématiques nous permettent de déterminer les propriétés d'un modèle. Et la science montre comment ces propriétés sont liées à la réalité. Parlons de notre science, de l'informatique. La réalité avec laquelle nous travaillons est des systèmes informatiques de différents types: processeurs, consoles de jeux, ordinateurs, exécution de programmes, etc. Je parlerai de l'exécution d'un programme sur un ordinateur, mais dans l'ensemble, toutes ces conclusions s'appliquent à n'importe quel système informatique. Dans notre science, nous utilisons de nombreux modèles différents: une machine de Turing, des ensembles d'événements partiellement ordonnés et bien d'autres.
Qu'est-ce qu'un programme? Il s'agit de tout code pouvant être considéré indépendamment. Supposons que nous devions écrire un navigateur. Nous effectuons trois tâches: nous concevons la présentation du programme pour l'utilisateur, puis nous écrivons un schéma de haut niveau du programme, et enfin nous écrivons le code. Lorsque nous écrivons le code, nous comprenons que nous devons écrire un outil pour formater le texte. Ici, nous devons à nouveau résoudre trois problèmes: déterminer quel texte cet outil retournera; choisissez un algorithme de formatage; écrire du code. Cette tâche a sa propre sous-tâche: insérer correctement les tirets dans les mots. Nous résolvons également cette sous-tâche en trois étapes - comme nous le voyons, elles sont répétées à plusieurs niveaux.
Examinons plus en détail la première étape: quel problème le programme résout. Ici, nous modélisons le plus souvent un programme comme une fonction qui reçoit une entrée et donne une sortie. En mathématiques, une fonction est généralement décrite comme un ensemble ordonné de paires. Par exemple, la fonction de quadrature des nombres naturels est décrite comme l'ensemble {<0,0>, <1,1>, <2,4>, <3,9>, ...}. La portée d'une telle fonction est l'ensemble des premiers éléments de chaque paire, c'est-à-dire les nombres naturels. Pour définir une fonction, nous devons spécifier sa portée et sa formule.
Mais les fonctions en mathématiques ne sont pas les mêmes que les fonctions dans les langages de programmation. Les mathématiques sont beaucoup plus simples. Étant donné que je n'ai pas le temps pour des exemples complexes, considérez-en un simple: une fonction en C ou une méthode statique en Java qui renvoie le plus grand diviseur commun de deux entiers. Dans la spécification de cette méthode, nous écrivons: calcule GCD(M,N) pour les arguments M et N , où GCD(M,N) est une fonction dont le domaine est l'ensemble de paires d'entiers, et la valeur de retour est le plus grand entier divisible par M et N Comment la réalité est-elle liée à ce modèle? Le modèle fonctionne avec des entiers, et en C ou Java, nous avons un entier 32 bits. Ce modèle nous permet de décider si l'algorithme GCD est correct, mais il n'empêchera pas les erreurs de débordement. Cela nécessiterait un modèle plus complexe, pour lequel il n'y a pas de temps.
Parlons des limites de la fonction en tant que modèle. Le travail de certains programmes (par exemple, les systèmes d'exploitation) ne se résume pas à retourner une certaine valeur pour certains arguments; ils peuvent être exécutés en continu. De plus, la fonction de modèle est mal adaptée à la deuxième étape: planifier une méthode pour résoudre le problème. Le tri rapide et le tri à bulles calculent la même fonction, mais ce sont des algorithmes complètement différents. Par conséquent, pour décrire la façon d'atteindre l'objectif du programme, j'utilise un modèle différent, appelons-le le modèle comportemental standard. Le programme qu'il contient est présenté comme l'ensemble de tous les comportements autorisés, chacun étant à son tour une séquence d'états et un état étant une affectation de valeurs à des variables.
Voyons à quoi ressemblera la deuxième étape de l'algorithme euclidien. Nous devons calculer GCD(M, N) . Nous initialisons M comme x et N comme y , puis soustrayons la plus petite de ces variables de la plus grande jusqu'à ce qu'elles soient égales. Par exemple, si M = 12 et N = 18 , nous pouvons décrire le comportement suivant:
[x = 12, y = 18] → [x = 12, y = 6] → [x = 6, y = 6]
Et si M = 0 et N = 0 ? Le zéro est divisible par tous les nombres, il n'y a donc pas de plus grand diviseur dans ce cas. Dans cette situation, nous devons revenir à la première étape et demander: avons-nous vraiment besoin de calculer le GCD pour les nombres non positifs? Si ce n'est pas nécessaire, il vous suffit de modifier la spécification.
Une petite digression sur la productivité devrait être faite ici. Elle est souvent mesurée par le nombre de lignes de code écrites par jour. Mais votre travail est beaucoup plus utile si vous vous débarrassez d'un certain nombre de lignes, car vous avez moins d'espace pour les bugs. Et le moyen le plus simple de se débarrasser du code est dans la première étape. Il est possible que vous n'ayez tout simplement pas besoin de toutes ces cloches et sifflets que vous essayez de mettre en œuvre. Le moyen le plus rapide de simplifier un programme et de gagner du temps est de ne pas faire des choses qui ne valent pas la peine. La deuxième étape est en deuxième position en termes de potentiel de gain de temps. Si vous mesurez la productivité par le nombre de lignes écrites, réfléchir à la façon de terminer la tâche vous rendra moins productif , car vous pouvez résoudre le même problème avec moins de code. Je ne peux pas donner de statistiques exactes ici, car je n'ai aucun moyen de calculer le nombre de lignes que je n'ai pas écrites parce que j'ai passé du temps sur la spécification, c'est-à-dire sur les première et deuxième étapes. Et l'expérience ne peut pas être mise ici non plus, car dans l'expérience nous n'avons pas le droit de terminer la première étape, la tâche est prédéterminée.
Dans les spécifications informelles, de nombreuses difficultés sont facilement ignorées. Il n'y a rien de compliqué à écrire des spécifications strictes pour les fonctions, je n'en discuterai pas. Au lieu de cela, nous parlerons de la rédaction de spécifications rigoureuses pour les modèles comportementaux standard. Il existe un théorème qui stipule que tout ensemble de comportements peut être décrit en utilisant la propriété de sécurité et la propriété de vivacité . La sécurité signifie que rien de mauvais ne se produira, le programme ne donnera pas la mauvaise réponse. La vitalité signifie que tôt ou tard quelque chose de bien se produira, c'est-à-dire que le programme donnera tôt ou tard la bonne réponse. En règle générale, la sécurité est un indicateur plus important; les erreurs surviennent le plus souvent ici. Par conséquent, pour gagner du temps, je ne parlerai pas de survie, même si, bien sûr, elle est également importante.
Nous atteignons la sécurité en prescrivant, premièrement, les nombreux états initiaux possibles. Et deuxièmement, les relations avec tous les prochains états possibles pour chaque état. Nous nous comportons comme des scientifiques et définissons les états mathématiquement. L'ensemble des états initiaux est décrit par la formule, par exemple, dans le cas de l'algorithme euclidien: (x = M) ∧ (y = N) . Pour certaines valeurs de M et N il n'y a qu'un seul état initial. La relation avec l'état suivant est décrite par une formule dans laquelle les variables de l'état suivant sont écrites avec un tiret et l'état actuel sans tiret. Dans le cas de l'algorithme euclidien, nous traiterons de la disjonction de deux formules, dans laquelle x est la plus grande valeur, et dans la seconde - y :
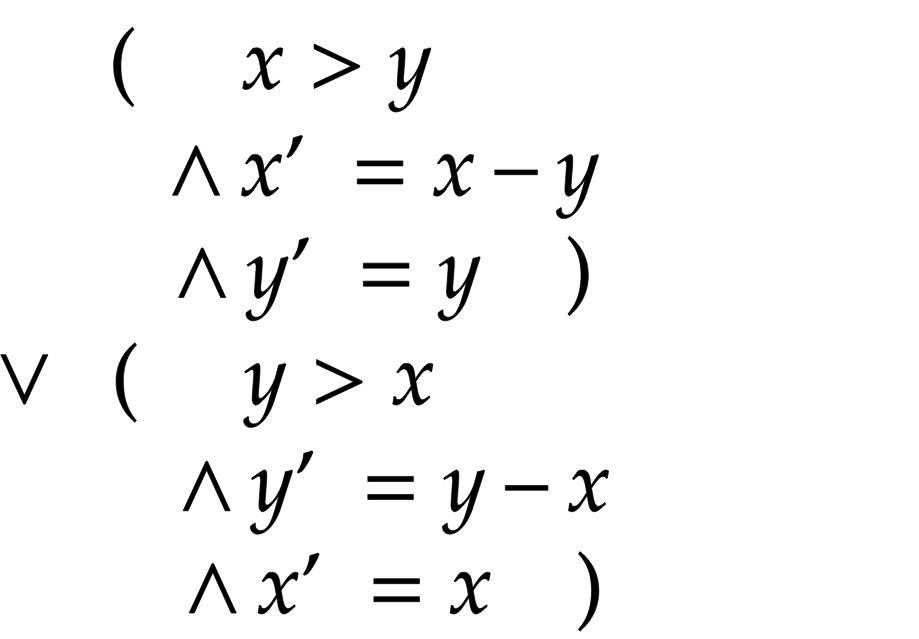
Dans le premier cas, la nouvelle valeur de y est égale à la valeur précédente de y, et nous obtenons la nouvelle valeur de x, en soustrayant la plus petite de la variable la plus grande. Dans le second cas, nous faisons le contraire.
Revenons à l'algorithme euclidien. Supposons encore que M = 12 , N = 18 . Ceci détermine le seul état initial, (x = 12) ∧ (y = 18) . Ensuite, nous substituons ces valeurs dans la formule ci-dessus et obtenons:

Voici la seule solution possible: x' = 18 - 12 ∧ y' = 12 , et on obtient le comportement: [x = 12, y = 18] . De la même manière, nous pouvons décrire tous les états de notre comportement: [x = 12, y = 18] → [x = 12, y = 6] → [x = 6, y = 6] .
Dans le dernier état [x = 6, y = 6] deux parties de l'expression seront fausses, par conséquent, elle n'a pas d'état suivant. Donc, nous avons la spécification complète de la deuxième étape - comme nous le voyons, ce sont des mathématiques assez ordinaires, comme celles des ingénieurs et des scientifiques, et pas étranges, comme en informatique.
Ces deux formules peuvent être combinées en une seule formule logique temporelle. Elle est élégante et facile à expliquer, mais maintenant elle n'a pas le temps. La logique temporelle dont nous pouvons avoir besoin uniquement pour la propriété de la vivacité, pour la sécurité, elle n'est pas nécessaire. La logique temporelle en tant que telle n'est pas agréable, ce n'est pas des mathématiques tout à fait ordinaires, mais dans le cas de la vivacité c'est un mal nécessaire.
Dans l'algorithme euclidien, pour chaque valeur de x et y il existe des valeurs uniques de x' et y' qui rendent vraie la relation avec l'état suivant. En d'autres termes, l'algorithme euclidien est déterministe. Pour simuler un algorithme non déterministe, il est nécessaire que l'état actuel ait plusieurs états futurs possibles, et que chaque valeur de la variable sans prime ait plusieurs valeurs de la variable avec un trait auquel la relation avec l'état suivant est vraie. Ce n'est pas difficile à faire, mais je ne donnerai pas d'exemples maintenant.
Pour créer un outil de travail, vous avez besoin de mathématiques formelles. Comment formaliser la spécification? Pour ce faire, nous avons besoin d'un langage formel, par exemple, TLA + . La spécification de l'algorithme euclidien dans ce langage ressemblera à ceci:

Le symbole de signe égal avec un triangle signifie que la valeur à gauche du signe est définie comme égale à la valeur à droite du signe. En substance, une spécification est une définition, dans notre cas deux définitions. Vous devez ajouter des déclarations et une syntaxe à la spécification dans TLA +, comme dans la diapositive ci-dessus. En ASCII, cela ressemblera à ceci:

Comme vous pouvez le voir, rien de compliqué. La spécification pour TLA + peut être vérifiée, c'est-à-dire contourner tous les comportements possibles dans un petit modèle. Dans notre cas, ce modèle sera certaines valeurs de M et N Il s'agit d'une méthode de vérification très efficace et facile qui s'exécute de manière entièrement automatique. De plus, vous pouvez écrire des preuves formelles de la vérité et les vérifier mécaniquement, mais cela prend beaucoup de temps, donc presque personne ne le fait.
Le principal inconvénient de TLA + est qu'il s'agit de mathématiques, et les programmeurs et les informaticiens ont peur des mathématiques. À première vue, cela ressemble à une blague, mais, malheureusement, je le dis avec sérieux. Mon collègue vient de me dire comment il a essayé d'expliquer TLA + à plusieurs développeurs. Dès que les formules sont apparues à l'écran, elles ont immédiatement eu des yeux en verre. Donc, si TLA + fait peur, vous pouvez utiliser PlusCal , c'est une sorte de langage de programmation de jouets. Une expression dans PlusCal peut être n'importe quelle expression TLA +, c'est-à-dire, dans l'ensemble, n'importe quelle expression mathématique. PlusCal a également une syntaxe pour les algorithmes non déterministes. Étant donné que toute expression TLA + peut être écrite en PlusCal, elle est beaucoup plus expressive de tout véritable langage de programmation. PlusCal est ensuite compilé dans la spécification TLA + facile à lire. Cela ne signifie pas, bien sûr, que la spécification complexe PlusCal se transformera en une simple sur TLA + - juste la correspondance entre eux est évidente, il n'y aura pas de complexité supplémentaire. Enfin, cette spécification peut être vérifiée avec les outils TLA +. En général, PlusCal peut aider à surmonter la phobie des mathématiques; il est facile à comprendre même pour les programmeurs et les informaticiens. Dans le passé, pendant un certain temps (environ 10 ans), j'ai publié des algorithmes dessus.
Peut-être que quelqu'un objectera que TLA + et PlusCal sont des mathématiques, et les mathématiques ne fonctionnent que sur des exemples inventés. En pratique, vous avez besoin d'un vrai langage avec des types, des procédures, des objets, etc. Ce n'est pas le cas. Voici ce que Chris Newcomb, qui a travaillé chez Amazon, écrit: «Nous avons utilisé TLA + dans dix grands projets, et dans chaque cas, son utilisation a contribué de manière significative au développement, parce que nous avons pu attraper des bogues dangereux avant d'entrer en production, et parce qu'il nous a donné la compréhension et la confiance nécessaires pour des optimisations de performance agressives qui n'affectent pas la vérité du programme . » Vous pouvez souvent entendre qu'en utilisant des méthodes formelles, nous obtenons un code inefficace - en pratique, tout est exactement le contraire. De plus, on pense que les gestionnaires ne peuvent pas être convaincus de la nécessité de méthodes formelles, même si les programmeurs sont convaincus de leur utilité. Et Newcomb écrit: «Les managers font maintenant tout leur possible pour écrire des spécifications pour TLA +, et ils y consacrent spécifiquement du temps . » Ainsi, lorsque les gestionnaires voient que TLA + fonctionne, ils sont heureux de l'accepter. Chris Newcomb l'a écrit il y a environ six mois (en octobre 2014), mais maintenant, pour autant que je sache, TLA + est utilisé dans 14 projets, et non 10. Un autre exemple concerne la conception de la XBox 360. Un stagiaire est venu chez Charles Thacker et a écrit spécification d'un système de mémoire. Grâce à cette spécification, un bug a été trouvé qui autrement n'aurait pas été remarqué, et à cause duquel chaque XBox 360 tomberait après quatre heures d'utilisation. Les ingénieurs d'IBM ont confirmé que leurs tests n'auraient pas détecté ce bogue.
Vous pouvez en savoir plus sur TLA + sur Internet et parlons maintenant des spécifications informelles. Nous devons rarement écrire des programmes qui calculent le diviseur le moins commun et autres. Plus souvent, nous écrivons des programmes comme l'outil jolie imprimante que j'ai écrit pour TLA +. Après le traitement le plus simple, le code TLA + ressemblerait à ceci:

Mais dans l'exemple ci-dessus, l'utilisateur souhaitait très probablement que la conjonction et les signes égaux soient alignés. Ainsi, la mise en forme correcte ressemblerait davantage à ceci:
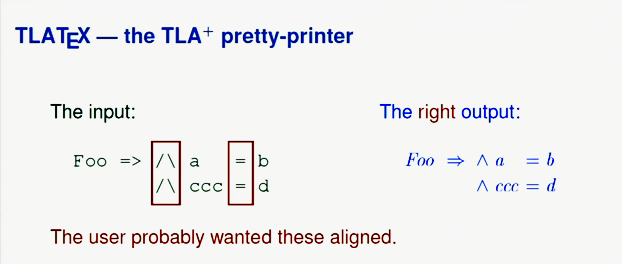
Prenons un autre exemple:

Ici, au contraire, l'alignement des signes égaux, l'addition et la multiplication dans la source étaient aléatoires, donc le traitement le plus simple est suffisant. En général, il n'y a pas de définition mathématique exacte du formatage correct, car «correct» dans ce cas signifie «ce que veut l'utilisateur», et cela ne peut pas être déterminé mathématiquement.
Il semblerait que si nous n'avons pas de définition de la vérité, alors la spécification est inutile. Mais ce n'est pas le cas. Si nous ne savons pas exactement ce que le programme doit faire, cela ne signifie pas que nous n'avons pas besoin de réfléchir à son travail - au contraire, nous devons consacrer encore plus d'efforts à cela. La spécification ici est particulièrement importante. Il est impossible de déterminer le programme optimal pour la liste structurelle, mais cela ne signifie pas que nous ne devrions pas le faire du tout, et écrire du code comme un flux de conscience n'est pas une chose. Au final, j'ai écrit une spécification de six règles avec des définitions sous forme de commentaires dans un fichier Java. Voici un exemple de l'une des règles: a left-comment token is LeftComment aligned with its covering token . Cette règle est écrite, disons, en anglais mathématique: LeftComment aligned , left-comment et LeftComment aligned covering token sont des termes avec des définitions. C'est ainsi que les mathématiciens décrivent les mathématiques: ils écrivent des définitions de termes et sur la base de ceux-ci - des règles. L'avantage de cette spécification est que la compréhension et le débogage des six règles sont beaucoup plus simples que 850 lignes de code. Je dois dire que la rédaction de ces règles n'a pas été facile, beaucoup de temps a été consacré à leur débogage. Surtout à cet effet, j'ai écrit du code qui indiquait quelle règle était utilisée. Étant donné que j'ai vérifié ces six règles avec quelques exemples, je n'ai pas eu besoin de déboguer 850 lignes de code, et les bogues se sont avérés assez faciles à trouver. Java dispose d'excellents outils pour cela. Si je venais d'écrire le code, cela me prendrait beaucoup plus de temps et le formatage se révélerait de moins bonne qualité.
Pourquoi était-il impossible d'utiliser une spécification formelle? D'une part, la bonne exécution n'est pas très importante ici. Une liste structurelle ne plaira à personne, donc je n'ai pas eu besoin de faire le bon travail dans toutes les situations inhabituelles. Plus important encore est le fait que je n'avais pas d'outils adéquats. L'outil pour tester les modèles TLA + est inutile ici, donc je devrais écrire manuellement des exemples.
La spécification donnée a des caractéristiques communes à toutes les spécifications. Il est d'un niveau supérieur à celui du code. Vous pouvez l'implémenter dans n'importe quelle langue. Pour l'écrire, tous les outils ou méthodes sont inutiles. Aucun cours de programmation ne vous aidera à rédiger cette spécification. Et il n'y a aucun outil qui pourrait rendre cette spécification inutile à moins, bien sûr, que vous n'écriviez un langage spécifiquement pour écrire des programmes de listage structurel sur TLA +. Enfin, cette spécification ne dit rien sur la façon exacte dont nous allons écrire le code, elle indique seulement ce que fait ce code. Nous écrivons une spécification pour nous aider à réfléchir au problème avant de commencer à penser au code.
Mais cette spécification présente également des caractéristiques qui la distinguent des autres spécifications. 95% des autres spécifications sont beaucoup plus courtes et plus simples:

De plus, cette spécification est un ensemble de règles. C'est généralement le signe d'une mauvaise spécification. Il est assez difficile de comprendre les conséquences d'un ensemble de règles, et c'est pourquoi j'ai dû passer beaucoup de temps à les déboguer. Cependant, dans ce cas, je n'ai pas pu trouver de meilleur moyen.
Il vaut la peine de dire quelques mots sur les programmes qui fonctionnent en continu. En règle générale, ils fonctionnent en parallèle, par exemple, des systèmes d'exploitation ou des systèmes distribués. Très peu de gens peuvent les comprendre dans leur esprit ou sur papier, et je ne suis pas l'un d'eux, bien que j'aie pu me le permettre une fois. Par conséquent, des outils sont nécessaires pour tester notre travail - par exemple, TLA + ou PlusCal.
Pourquoi aviez-vous besoin d'écrire une spécification si je savais déjà exactement ce que le code devrait faire? En fait, il me semblait seulement que je le savais. De plus, s'il existe une spécification, un étranger n'a plus besoin d'entrer dans le code pour comprendre exactement ce qu'il fait. J'ai une règle: il ne devrait pas y avoir de règles générales. Cette règle, bien sûr, a une exception, c'est la seule règle générale que je suive: la spécification de ce que fait le code devrait dire aux gens tout ce qu'ils doivent savoir lorsqu'ils utilisent ce code.
Alors, que doivent exactement savoir les programmeurs pour penser? Pour commencer, la même chose que tout le monde: si vous n'écrivez pas, alors vous pensez seulement que vous pensez. De plus, vous devez réfléchir avant de coder, ce qui signifie que vous devez écrire avant de coder. Une spécification est ce que nous écrivons avant de commencer à coder. La spécification est nécessaire pour tout code pouvant être utilisé ou modifié par n'importe qui. Et ce «quelqu'un» peut s'avérer être l'auteur du code un mois après l'avoir écrit. La spécification est nécessaire pour les grands programmes et systèmes, pour les classes, pour les méthodes et parfois même pour les sections complexes d'une seule méthode. Que faut-il exactement écrire sur le code? Il est nécessaire de décrire ce qu'il fait, c'est-à-dire quelque chose qui peut être utile à toute personne utilisant ce code. Parfois, il peut également être nécessaire d'indiquer exactement comment le code atteint son objectif. Si nous avons réussi cette méthode au cours des algorithmes, alors nous l'appelons un algorithme. Si c'est quelque chose de plus spécial et de nouveau, nous l'appelons un design de haut niveau. Il n'y a pas de différence formelle: les deux sont un modèle abstrait du programme.
Comment exactement une spécification de code doit-elle être écrite? L'essentiel: il doit être supérieur d'un niveau au code lui-même. Il doit décrire les états et les comportements. Elle doit être aussi stricte que la tâche l'exige. Si vous écrivez une spécification sur la façon d'implémenter la tâche, elle peut être écrite en pseudo-code ou en utilisant PlusCal. Apprendre à rédiger des spécifications est nécessaire sur des spécifications formelles. Cela vous donnera les compétences nécessaires qui vous aideront, y compris celles avec des compétences informelles. Et comment apprendre à rédiger des spécifications formelles? Lorsque nous avons appris la programmation, nous avons écrit des programmes puis les avons débogués. : , . TLA+, , , . TLA+ , .
? , . , . , .
, . , , . , . . , , . , . , .
— . — Amazon. . ? . , , . , . — , . . .
. - , , . , - , , . . , . , , . , ? -, , , , . , . , . , , . -, , . . , , .
, , . - . , — . , , . , , , , . . , . , , — . , .
TLA+ PlusCal , . , .
, . — , . , Hydra 2019, 11-12 2019 -. .