Introduction aux réseaux de neurones convolutifs

Le cours complet de russe se trouve sur ce lien .
Le cours d'anglais original est disponible sur ce lien .


De nouvelles conférences sont prévues tous les 2-3 jours.

Entretien avec Sebastian

- Donc, nous sommes à nouveau avec Sebastian dans la troisième partie de ce cours. Sebastian, je sais que vous avez fait beaucoup de développement en utilisant des réseaux de neurones convolutifs. Pouvez-vous nous en dire un peu plus sur ces réseaux et quels sont-ils? Je suis sûr que les étudiants de notre cours écouteront avec autant d'intérêt, car dans cette partie ils devront développer eux-mêmes le réseau neuronal convolutif.
- Génial! Ainsi, les réseaux de neurones convolutifs sont un excellent moyen de structurer le réseau, de construire la soi-disant invariance (attribution de caractéristiques immuables). Par exemple, prenez l'idée de la reconnaissance des motifs sur scène ou sur une photo, vous voulez comprendre si Sebastian y est représenté ou non. Peu importe dans quelle partie de la photo je me trouve, où se trouve ma tête - au centre de la photo ou dans le coin. La reconnaissance de ma tête, mon visage devrait se produire indépendamment de l'endroit où ils se trouvent dans l'image. C'est l'invariance, la variabilité de l'emplacement, qui est réalisée par les réseaux de neurones convolutionnels.
- Très intéressant! Pouvez-vous nous dire les principales tâches dans lesquelles les réseaux de neurones convolutionnels sont utilisés?
- Les réseaux de neurones convolutifs sont assez étroitement utilisés lorsque vous travaillez avec de l'audio et de la vidéo, y compris des images médicales. Ils sont également utilisés dans les technologies langagières, où les spécialistes utilisent l'apprentissage profond pour comprendre et reproduire les constructions langagières. En fait, il y a beaucoup d'applications pour cette technologie, je dirais même qu'elles sont infinies! Sa technologie peut être utilisée en finance et dans tout autre domaine.
«J'ai utilisé des réseaux de neurones convolutifs pour analyser les images satellites.»
- Génial! La tâche standard!
- Que pensez-vous, pouvons-nous considérer les réseaux de neurones convolutifs comme quelque chose comme le dernier et le plus avancé outil dans le développement de l'apprentissage profond?
- Ha! J'ai déjà appris à ne jamais dire jamais. Il y aura toujours quelque chose de nouveau et d'étonnant!
"Donc nous avons encore du travail à faire?" :)
- Il y aura assez de travail!
- Excellent! Dans ce cours, nous ne faisons qu'enseigner aux futurs pionniers de l'apprentissage automatique. Avez-vous des souhaits pour nos étudiants avant qu'ils ne commencent à construire leur premier réseau neuronal convolutionnel?
- Voici un fait intéressant pour vous. Les réseaux de neurones convolutifs ont été inventés en 1989, et cela fait très longtemps! La plupart d'entre vous n'étaient même pas nés à ce moment-là, ce qui signifie que ce n'est pas le génie de l'algorithme qui compte, mais les données sur lesquelles l'algorithme fonctionne. Nous vivons dans un monde où il y a beaucoup de données à analyser et à rechercher des modèles. Nous avons la capacité d'émuler les fonctions de l'esprit humain en utilisant cette énorme quantité de données. Lorsque vous travaillez sur des réseaux de neurones convolutifs, essayez de vous concentrer sur la recherche des bonnes données et de leur application - voyez ce qui se passe et parfois cela peut se révéler être de la vraie magie, comme ce fut le cas dans notre cas lorsque nous résolvions le problème de la détection du cancer de la peau.
- Génial! Eh bien, passons enfin à la magie!

Présentation

Dans la dernière leçon, nous avons appris à développer des réseaux de neurones profonds capables de classer des images d'éléments vestimentaires à partir de l'ensemble de données Fashion MNIST.



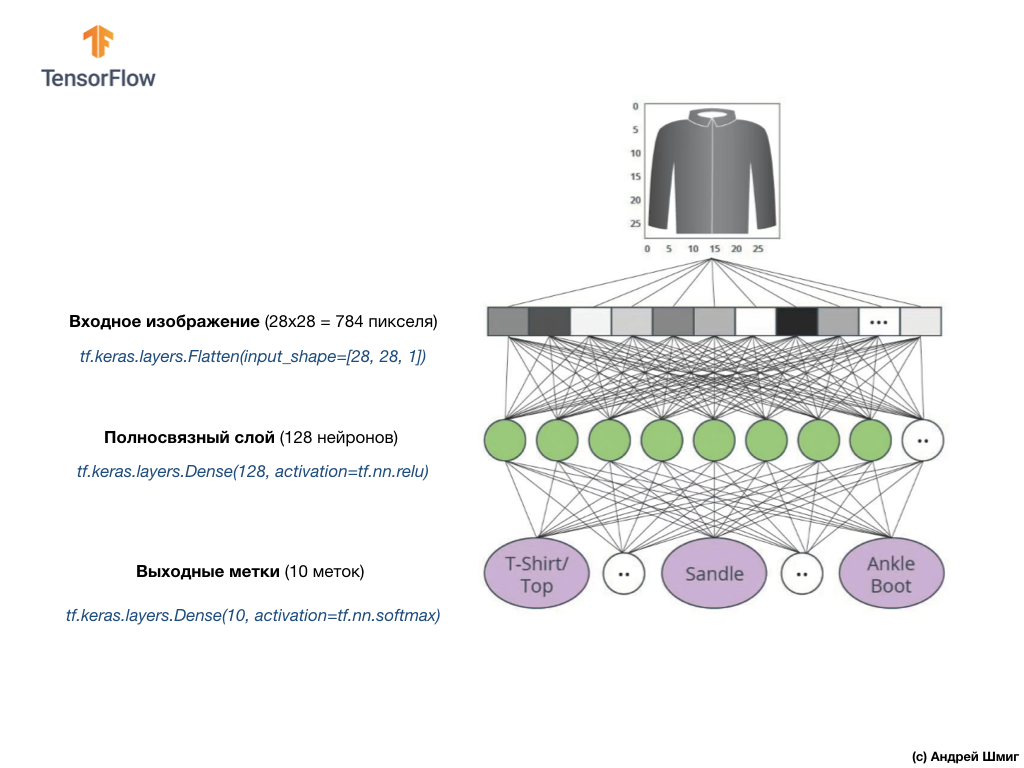
Les résultats que nous avons obtenus en travaillant sur le réseau neuronal étaient impressionnants - précision de classification de 88%. Et cela en quelques lignes de code (sans tenir compte du code de construction de graphiques et d'images)!

model = tf.keras.Sequential([ tf.keras.layers.Flatten(input_shape=(28, 28, 1)), tf.keras.layers.Dense(128, activation=tf.nn.relu), tf.keras.layers.Dense(10, activation=tf.nn.softmax) ]) 

 model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy']) 

 NUM_EXAMPLES = 60000 train_dataset = train_dataset.repeat().shuffle(NUM_EXAMPLES).batch(32) test_dataset = test_dataset.batch(32) 

 model.fit(train_dataset, epochs=5, steps_per_epoch=math.ceil(num_train_examples/32)) 

 test_loss, test_accuracy = model.evaluate(test_dataset, steps=math.ceil(num_test_examples/32)) print(': ', test_accuracy) 

: 0.8782

Nous avons également expérimenté l'effet du nombre de neurones dans les couches cachées et du nombre d'itérations d'entraînement sur la précision du modèle. Mais comment rendre ce modèle encore meilleur et plus précis? Une façon d'y parvenir consiste à utiliser des réseaux de neurones convolutifs, en abrégé SNA. Le SNA montre une plus grande précision dans la résolution des problèmes de classification d'images que les réseaux neuronaux entièrement connectés standard que nous avons rencontrés dans les classes précédentes. C'est pour cette raison que le SNA est devenu si populaire et c'est grâce à eux qu'une percée technologique dans le domaine de la vision industrielle est devenue possible.

Dans cette leçon, nous apprendrons à quel point il est facile de développer un classificateur SNA à partir de zéro à l'aide de TensorFlow et Keras. Nous utiliserons le même jeu de données Fashion MNIST que nous avons utilisé dans la leçon précédente. À la fin de cette leçon, nous comparons la précision de la classification des éléments vestimentaires du réseau neuronal précédent avec le réseau neuronal convolutionnel de cette leçon.

Avant de vous plonger dans le développement, il vaut mieux approfondir le principe de fonctionnement des réseaux de neurones convolutifs.

Deux concepts de base dans les réseaux de neurones convolutionnels:

• convolution
• opération de sous-échantillonnage (pooling, max pooling)

Examinons-les de plus près.

Convolution

Dans cette partie de notre leçon, nous apprendrons une technique appelée convolution. Voyons comment cela fonctionne.

Prenez une image dans des tons de gris et, par exemple, imaginez que ses dimensions sont de 6 px de hauteur et 6 px de largeur.



Notre ordinateur interprète l'image comme un tableau bidimensionnel de pixels. Étant donné que notre image est dans des tons de gris, la valeur de chaque pixel sera comprise entre 0 et 255. 0 - noir, 255 - blanc.

Dans l'image ci-dessous, nous voyons une représentation de l'image 6px x 6px et les valeurs de pixels correspondantes:



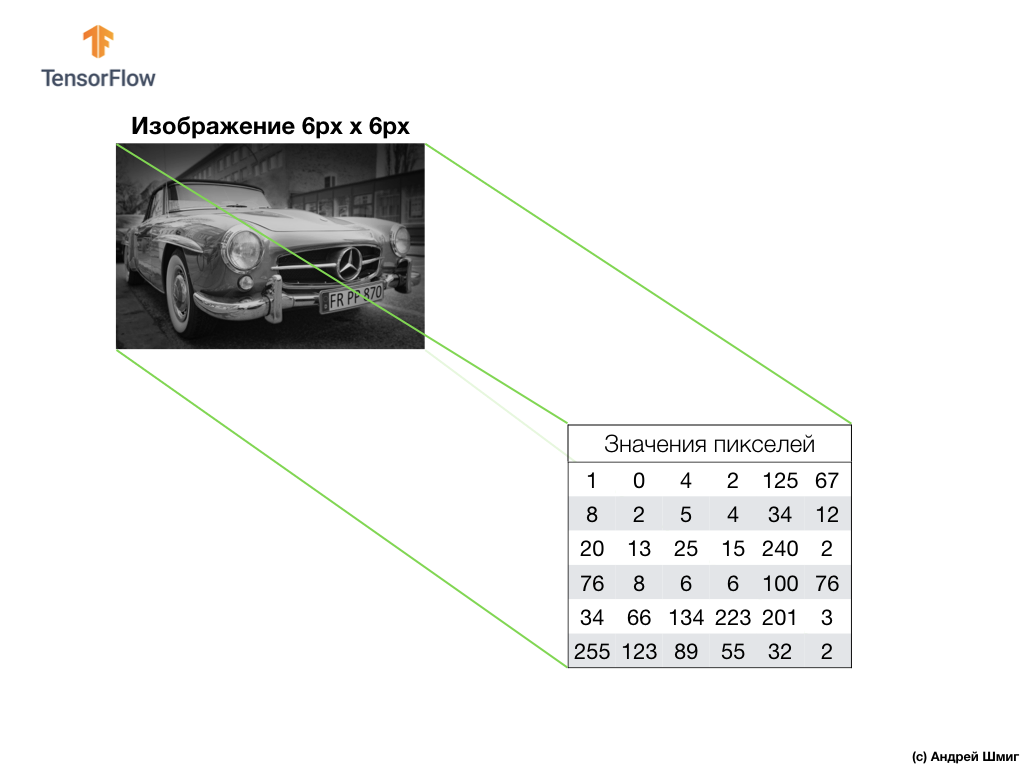
Comme vous le savez déjà, avant de travailler avec des images, vous devez normaliser les valeurs de pixels - amenez les valeurs à un intervalle de 0 à 1. Cependant, dans cet exemple, pour des raisons d'explication, nous enregistrerons les valeurs de pixels de l'image et ne les normaliserons pas.

L'essence de la convolution est de créer un autre ensemble de valeurs, appelé noyau ou filtre. Un exemple peut être vu dans l'image ci-dessous - une matrice 3 x 3:



Ensuite, nous pouvons scanner notre image en utilisant le noyau. Les dimensions de notre image sont 6x6px, et les noyaux sont 3x3px. La couche convolutionnelle est appliquée au cœur et à chaque section de l'image d'entrée.

Imaginons que nous voulons convolutionner sur un pixel avec une valeur de 25 (3 lignes, 3 colonnes) et la première chose à faire est de centrer le noyau sur ce pixel:



Dans l'image, l'emplacement du noyau est surligné en jaune. Maintenant, nous ne regarderons que les valeurs de pixels qui sont dans notre rectangle jaune, dont les tailles correspondent aux tailles de notre noyau de convolution.

Maintenant, nous prenons les valeurs de pixels de l'image et du noyau, multiplions chaque pixel de l'image par le pixel correspondant du noyau et ajoutons toutes les valeurs de produit, et attribuons la valeur de pixel résultante à la nouvelle image.







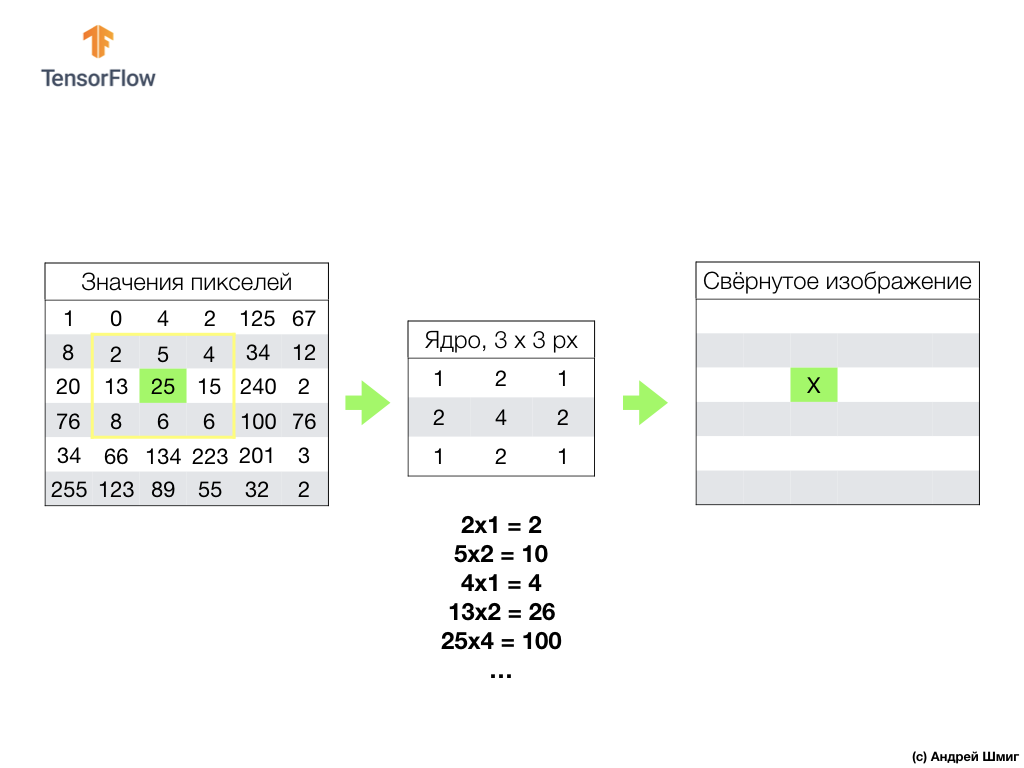
Nous effectuons une opération similaire avec tous les pixels de notre image. Mais que devrait-il arriver aux pixels aux bordures?



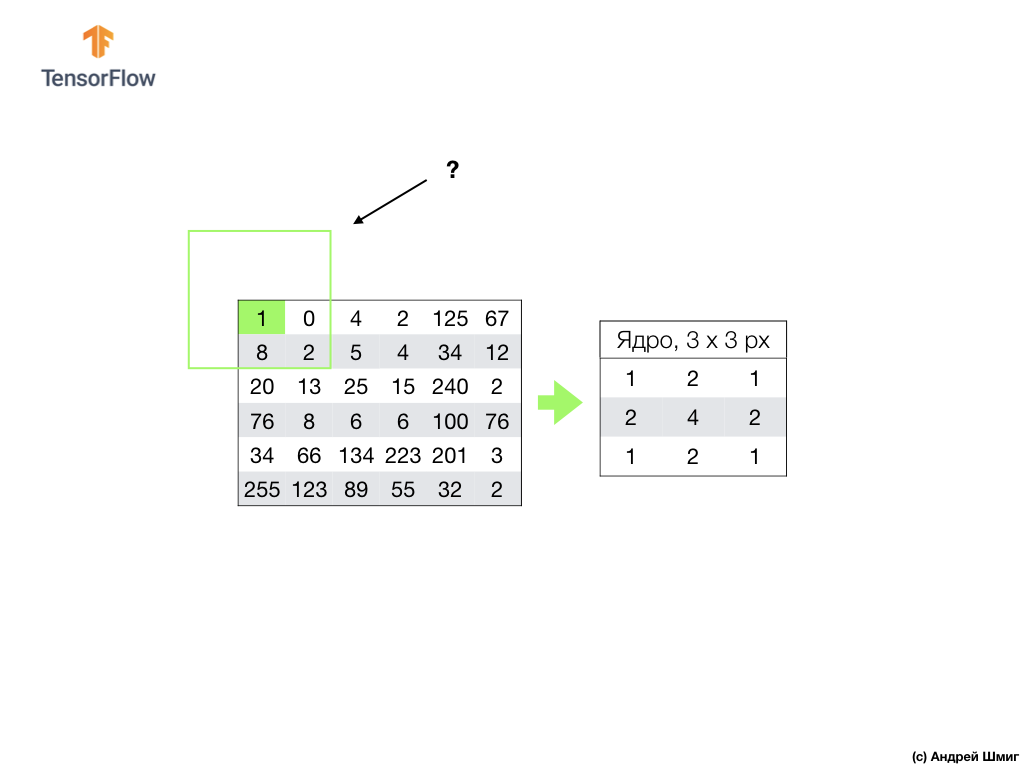
Il existe plusieurs solutions. Premièrement, nous pouvons simplement ignorer ces pixels, mais dans ce cas, nous perdrons des informations sur l'image, qui peuvent se révéler importantes, et l'image minimisée deviendra plus petite que l'original. Deuxièmement, nous pouvons simplement "tuer" avec des valeurs nulles les pixels dont les valeurs fondamentales dépassent le cadre de l'image. Le processus est appelé alignement.



Maintenant que nous avons effectué l'alignement avec des valeurs de pixel nul, nous pouvons calculer la valeur du pixel final dans l'image minimisée comme précédemment.

Une convolution est le processus d'application d'un noyau (filtre) à chaque partie de l'image d'entrée, par analogie avec une couche entièrement connectée (couche dense), nous verrons que la convolution est la même couche dans Keras.

Examinons maintenant le deuxième concept des réseaux de neurones convolutifs - le fonctionnement du sous-échantillonnage (pooling, max-pooling).

Opération de sous-échantillonnage (pooling, max-pooling)

Nous allons maintenant considérer le deuxième concept fondamental qui sous-tend les réseaux de neurones convolutifs - le fonctionnement du sous-échantillonnage (pooling, max-pooling). En termes simples, une opération de sous-échantillonnage est le processus de compression (réduction de taille) d'une image en ajoutant les valeurs des blocs de pixels. Voyons comment cela fonctionne sur un exemple concret.



Pour effectuer l'opération de sous-échantillonnage, nous devons décider de deux composantes de ce processus - la taille de l'échantillon (la taille de la grille rectangulaire) et la taille de l'étape. Dans cet exemple, nous utiliserons une grille rectangulaire 3x3 et l'étape 3. Cette étape détermine le nombre de pixels par lesquels la grille rectangulaire doit être décalée lors de l'exécution de l'opération de sous-échantillonnage.

Après avoir décidé de la taille de la grille et de la taille des pas, nous devons trouver la valeur maximale de pixels qui tombe dans la grille sélectionnée. Dans l'exemple ci-dessus, les valeurs 1, 0, 4, 8, 2, 5, 20, 13, 25 tombent dans la grille. La valeur maximale est 25. Cette valeur est «transférée» vers la nouvelle image. La grille est décalée de 3 pixels vers la droite et le processus de sélection de la valeur maximale et de transfert vers une nouvelle image est répété.



Par conséquent, une image plus petite sera obtenue par rapport à l'image d'entrée d'origine. Dans notre exemple, une image a été obtenue qui est la moitié de la taille de notre image d'origine. La taille de l'image finale variera en fonction du choix de la taille de la grille rectangulaire et de la taille des pas.

Voyons comment cela fonctionnera en Python!

Résumé

Nous nous sommes familiarisés avec des concepts tels que la convolution et l'opération de mise en commun maximale.

La convolution est le processus d'application d'un filtre («noyau») à une image. L'opération de sous-échantillonnage par valeur maximale est le processus de réduction de la taille d'une image en combinant un groupe de pixels en une seule valeur maximale de ce groupe.

Comme nous le verrons dans la partie pratique, la couche convolutionnelle peut être ajoutée au réseau neuronal en utilisant la couche Conv2D dans Keras. Cette couche est similaire à la couche dense et contient des pondérations et des décalages qui subissent une optimisation (sélection). Conv2D couche Conv2D contient également des filtres ("noyaux"), dont les valeurs sont également optimisées. Ainsi, dans la couche Conv2D , les valeurs à l'intérieur de la matrice de filtre sont les variables qui subissent une optimisation.

Quelques termes que nous avons réussi à trouver:

• SNS - réseaux de neurones convolutifs. Un réseau de neurones qui contient au moins une couche convolutionnelle. Un SCN typique contient d'autres couches, telles que des couches d'échantillons et des couches entièrement connectées.
• La convolution est le processus d'application d'un filtre («noyau») à une image.
• Un filtre (noyau) est une matrice de taille plus petite que les données d'entrée, destinée à convertir les données d'entrée en blocs.
• L'alignement est le processus consistant à ajouter, le plus souvent des valeurs nulles, aux bords d'une image.
• L'opération de sous-échantillonnage est le processus de réduction de la taille d'une image grâce à l'échantillonnage. Il existe plusieurs types de couches de sous-échantillonnage, par exemple, une couche de sous-échantillonnage moyenne (échantillonnage d'une valeur moyenne), cependant, un sous-échantillonnage par la valeur maximale est le plus souvent utilisé.
• Le sous-échantillonnage par la valeur maximale est le processus de sous-échantillonnage, au cours duquel de nombreuses valeurs sont converties en une seule valeur - le maximum parmi l'échantillonnage.
• Étape - le nombre de pixels de déplacement par le filtre (noyau) dans l'image.
• Échantillonnage (sous-échantillonnage) - processus de réduction de la taille de l'image.

CoLab: classification des éléments vestimentaires Fashion MNIST à l'aide d'un réseau neuronal convolutionnel

Nous avons été encerclés autour d'un doigt! Il est logique d'exécuter cette partie pratique uniquement après la fin de la partie précédente - tout le code, à l'exception d'un bloc, reste le même. La structure de notre réseau neuronal est en train de changer, et ce sont quatre lignes supplémentaires pour les couches neuronales convolutionnelles et les couches de sous-échantillonnage à la valeur maximale (max-pooling).

 model = tf.keras.Sequential([ tf.keras.layers.Conv2D(32, (3,3), padding='same', activation=tf.nn.relu, input_shape=(28, 28, 1)), tf.keras.layers.MaxPooling2D((2, 2), strides=2), tf.keras.layers.Conv2D(64, (3,3), padding='same', activation=tf.nn.relu), tf.keras.layers.MaxPooling2D((2, 2), strides=2), tf.keras.layers.Flatten(), tf.keras.layers.Dense(128, activation=tf.nn.relu), tf.keras.layers.Dense(10, activation=tf.nn.softmax) ]) 

Toutes les explications détaillées sur la façon de travailler, ils promettent de nous donner dans la partie suivante - 4 parties.

Ah oui. La précision du modèle au stade de la formation est devenue égale à 97% (le modèle «recyclé» à des epochs=10 ), et lors de l'examen de l'ensemble de données pour les tests, il a montré exactement 91%. Une augmentation notable de la précision par rapport à l'architecture précédente, où nous n'utilisions que des couches entièrement connectées - 88%.

Résumé

Dans cette partie de la leçon, nous avons étudié un nouveau type de réseau neuronal - réseau neuronal convolutionnel. Nous nous sommes familiarisés avec des termes tels que «convolution» et «opération de mise en commun maximale», avons développé et formé un réseau neuronal convolutionnel à partir de zéro. En conséquence, nous avons vu que notre réseau neuronal convolutionnel produit plus de précision que le réseau neuronal que nous avons développé dans la dernière leçon.

PS Note de l'auteur de la traduction.

Le cours est intitulé "Introduction à l'apprentissage en profondeur à l'aide de TensorFlow", nous ne nous plaindrons donc pas du manque d'explications détaillées du principe des réseaux de neurones convolutifs (couches) - les deux prochains articles porteront sur le principe de fonctionnement du réseau de neurones convolutifs et leur structure interne (les articles ne concernent pas le cours, mais ont été recommandés par les participants de StackOverflow pour une meilleure compréhension de ce qui se passe).

... et appel à l'action standard - inscrivez-vous, mettez un plus et partagez :)
YouTube
Télégramme
VKontakte