
Depuis sa sortie en août 2018, Julia a activement gagné en popularité en entrant les 10 meilleures langues sur Github et les 20 compétences professionnelles les plus populaires selon Upwork . Pour les débutants, les cours commencent et les livres sont publiés . Julia est utilisée pour la planification de missions spatiales , la pharmacométrie et la modélisation du climat .
Avant de passer à l'informatique distribuée dans Julia, tournons-nous vers l'expérience de ceux qui ont déjà tenté cette opportunité d'un nouveau PL pour les problèmes appliqués - de l'équation de diffusion sur deux cœurs aux cartes astronomiques sur un supercalculateur.
Calcul parallèle et facteurs affectant les performances du calcul parallèle
La plupart des ordinateurs modernes ont plus d'un processeur et plusieurs ordinateurs peuvent être combinés en un cluster. L'utilisation de la puissance de plusieurs processeurs vous permet d'effectuer de nombreux calculs plus rapidement. Les performances sont affectées par deux facteurs principaux: la vitesse des processeurs eux-mêmes et la vitesse de leur accès à la mémoire. Dans un cluster, ce processeur aura l'accès le plus rapide à la RAM située sur le même ordinateur ou hôte. Encore plus surprenant, de tels problèmes sont pertinents sur un ordinateur portable multicœur typique en raison des différences de vitesse de la mémoire principale et du cache. Par conséquent, un bon environnement multiprocesseur devrait vous permettre de contrôler l'utilisation d'une partie de la mémoire par un processeur spécifique.
Informatique parallèle dans Julia
Julia possède plusieurs primitives intégrées pour le calcul parallèle à chaque niveau: vectorisation (SIMD), multithreading et calcul distribué.
Le multithreading de Julia permet à l'utilisateur d'utiliser les capacités d'un ordinateur portable multicœur, tandis que les primitives d'appel et d'accès à distance vous permettent de répartir le travail entre de nombreux processus du cluster. En plus de ces primitives intégrées, un certain nombre de packages dans l'écosystème Julia offrent un traitement parallèle efficace.
Vectorisation automatique dans Julia
Les puces Intel modernes fournissent un certain nombre d'extensions de jeux de commandes. Parmi eux, différentes versions de l'extension Streaming SIMD (SSE) et plusieurs générations d'extensions vectorielles (disponibles dans les dernières familles de processeurs). Ces extensions fournissent une programmation dans le style des données multiples à instruction unique (SIMD) , fournissant une accélération significative pour le code qui se prête à un tel style de programmation. Le puissant compilateur Julia de LLia peut générer automatiquement un code machine très efficace pour les fonctions de base et définies par l'utilisateur sur n'importe quelle architecture, comme le matériel SIMD (pris en charge par LLVM ), ce qui permet à l'utilisateur de se soucier moins d'écrire du code spécialisé pour chacune de ces architectures. Un autre avantage de l'utilisation du compilateur pour améliorer les performances, plutôt que de coder manuellement les "boucles actives" dans un assemblage, est qu'il est nettement meilleur pour l'avenir. Chaque fois que l'architecture du jeu d'instructions de nouvelle génération sort, le code personnalisé Julia devient automatiquement plus rapide.
Multithreading
Le multithreading dans Julia prend généralement la forme de boucles parallèles. Il existe également des primitives pour les verrous et les composants atomiques qui permettent aux utilisateurs de synchroniser leur code. Les primitives parallèles de Julia sont simples mais puissantes. Il est démontré qu'ils évoluent vers des milliers de nœuds et traitent des téraoctets de données .
Informatique distribuée
Bien que les primitives intégrées de Julia soient suffisantes pour les déploiements parallèles à grande échelle, il existe un certain nombre de packages pour des travaux plus spécialisés. ClusterManagers.jl fournit des interfaces pour un certain nombre de systèmes de mise en file d'attente des travaux couramment utilisés dans les clusters informatiques, tels que Sun Grid Engine et Slurm . DistributedArrays.jl fournit une interface pratique pour les tableaux de données distribués sur un cluster. Cela combine les ressources mémoire de plusieurs machines, ce qui permet d'utiliser des baies trop volumineuses pour tenir sur une seule machine. Chaque processus s'exécute sur la partie du tableau qu'il possède, fournissant une réponse toute faite à la question de savoir comment le programme doit être divisé entre les machines.
Dans certaines applications héritées, les utilisateurs préfèrent ne pas repenser leur modèle parallèle et souhaitent continuer à utiliser la concurrence de style MPI . Pour eux, MPI.jl fournit une enveloppe fine autour de MPI qui permet aux utilisateurs d'utiliser des procédures de passage de messages de style MPI.
Julia au combat
Le projet Celeste est une collaboration entre Julia Computing, Intel Labs, JuliaLabs @ MIT, Lawrence Berkeley National Labs et l'Université de Californie à Berkeley.
Celeste est un modèle hiérarchique entièrement génératif qui utilise l'inférence statistique pour déterminer mathématiquement l'emplacement et les caractéristiques des sources de lumière dans le ciel. Ce modèle permet aux astronomes d'identifier des galaxies prometteuses pour cibler les spectrographes et aide à comprendre le rôle de l'énergie noire, de la matière noire et de la géométrie de l'univers.

Exemple de Sloan Digital Sky Survey (SDSS)
En utilisant les propres capacités de calcul parallèle de Julia, l'équipe de recherche de Celeste a traité 55 téraoctets de données visuelles et classé 188 millions d'objets astronomiques en seulement 15 minutes, ce qui a donné le premier catalogue complet de tous les objets visibles de Sloan Digital Sky Survey . C'est l'un des plus gros problèmes d'optimisation mathématique jamais résolus par l'humanité.

Le projet Celeste a utilisé 9 300 nœuds Knights Landing (KNL) sur le supercalculateur NERSC Cori Phase II pour exécuter 1,3 million de threads sur 650 000 noyaux KNL, ce qui a combiné la liste des applications avec des vitesses dépassant 1 pétaflops par seconde , faisant de Julia la seule dynamique un langage de haut niveau qui a jamais réalisé un tel exploit. ?? Mais la synchronisation des télescopes et le traitement des données pour une image de trou noir le 10.04.19 ont-ils battu ce record? Il semble que Python y soit principalement utilisé.
Programmation parallèle avec Julia à l'aide de MPI
Traduction de matériel du blog Claudio sur la physique des plasmas 2018-09-30
Julia existe depuis 2012, et après plus de six ans de développement, la version 1.0 est enfin sortie. C'est une étape importante qui m'a inspiré pour créer un nouveau post (après plusieurs mois de silence). Cette fois, nous verrons comment faire de la programmation parallèle dans Julia en utilisant le paradigme MPI (Message Passing Interface) via la bibliothèque open source Open MPI. Nous le ferons en résolvant un vrai problème physique: la diffusion de chaleur à travers une région bidimensionnelle.

Figure 1. Supercalculateur Sequoia en LLNL avec près de 1,6 million de processeurs disponibles pour la simulation numérique des armes nucléaires. hpc.llnl.gov
Ce sera une application MPI assez avancée, destinée à ceux qui ont déjà une certaine compréhension de l'informatique parallèle. Pour cette raison, je ne vais pas aller pas à pas, mais plutôt me concentrer sur des aspects spécifiques qui, à mon avis, sont intéressants (en particulier, l'utilisation de cellules fantômes et la transmission de messages dans une grille bidimensionnelle). Conformément à la tradition de ses récents articles, le code dont il est question ici ne sera présenté que partiellement. Ceci est accompagné d'une solution complète que vous pouvez trouver sur Github - Diffusion.jl .
L'informatique parallèle est entrée dans le «monde commercial» au cours des dernières années. Il s'agit d'une solution standard pour les applications ETL (Extract-Transform-Load), où le problème considéré est embarrassamment parallèle: chaque processus est effectué indépendamment de tous les autres, et aucune connexion réseau n'est requise (jusqu'à ce que l'étape finale de «réduction» se produise, où chaque solution locale est assemblée dans solution globale).
Dans de nombreuses applications scientifiques, il est nécessaire de transmettre des informations via un réseau de clusters. Ces problèmes de «compression parallèle» sont souvent des simulations numériques: problèmes d'astrophysique, de modélisation météorologique, de biologie, de systèmes quantiques, etc. Dans certains cas, ces simulations sont effectuées sur des dizaines, voire des millions de processeurs (Fig. 1), et la mémoire est répartie entre différents processeurs. En règle générale, ces processeurs interagissent dans un supercalculateur via le paradigme MPI (Message Passing Interface).
Quiconque travaille dans l'informatique haute performance doit être familier avec MPI. Il permet d'utiliser l'architecture de cluster à un niveau très bas. Théoriquement, un chercheur peut attribuer à chaque CPU sa propre charge de calcul. Il / elle peut décider exactement quand et quelles informations doivent être transférées entre les processeurs, et si cela doit se produire de manière synchrone ou asynchrone.
Et maintenant, revenons au contenu de cet article, où nous verrons comment écrire une solution à une équation de type diffusion en utilisant MPI. Nous avons déjà discuté d'un schéma explicite pour une équation unidimensionnelle de ce type ( Au fait, nous en avons également discuté ). Cependant, dans cet article, nous considérerons une solution bidimensionnelle.
Le code Julia présenté ici est essentiellement une traduction du code C / Fortran expliqué dans ce magnifique post de Fabien Durnak.
Dans cet article, je n'analyserai pas en détail la vitesse de mise à l'échelle et le nombre de processeurs. Principalement parce que je n'ai que deux processeurs avec lesquels je peux jouer à la maison (processeur Intel Core i7 sur mon MacBook Pro) ... Cependant, je peux toujours dire avec fierté que le code Julia présenté dans cet article, montre une accélération significative lors de l'utilisation de deux processeurs contre un. Quoi qu'il en soit: c'est plus rapide que les codes Fortran et C équivalents! (plus à ce sujet plus tard)
Voici les sujets que nous allons couvrir dans cet article:
- Julia: Mes premières impressions
- Comment installer Open MPI sur votre ordinateur
- Problème: propagation à travers un domaine bidimensionnel
- Communication entre processeurs: le besoin de cellules fantômes
- Utilisation de MPI
- Visualisation de la solution
- Performances
- Conclusions
1. Premières impressions de Julia
En fait, j'ai rencontré Julia récemment, j'ai donc décidé de me concentrer sur quelques «premières impressions» ici.
La principale raison pour laquelle je me suis intéressée à Julia est qu'elle promet d'être un framework à usage général avec des performances comparables à C et Fortran , tout en préservant la flexibilité et la facilité d'utilisation des langages de script tels que Matlab ou Python . En fait, Julia devrait être capable d'écrire des applications Data Science / High-Performance-Computing qui s'exécutent sur l'ordinateur local, dans le cloud ou sur des superordinateurs d'entreprise.
Un aspect que je n'aime pas est le workflow, qui semble sous-optimal pour ceux qui, comme moi, utilisent IntelliJ et PyCharm quotidiennement (le plugin IntelliJ Julia est terrible). J'ai également essayé le Juno IDE , qui est probablement la meilleure solution pour le moment, mais je dois encore m'y habituer.
Un aspect qui montre à quel point Julia n'est pas encore arrivée à sa «maturité» est la diversité et la désuétude de la documentation de nombreux paquets ( pour les paquets qui ont été maintenus à flot, tout a été pelleté depuis l'année dernière ). Je n'ai toujours pas trouvé de moyen d'écrire une matrice de nombres à virgule flottante sur le disque sous une forme formatée ( maintenant c'est facile à trouver ). Bien sûr, vous pouvez écrire sur le disque chaque élément de la matrice dans une boucle double, mais de meilleures solutions devraient être disponibles. C'est juste que cette information est difficile à trouver, et la documentation doit être complète.
Un autre aspect qui se démarque la première fois que Julia est utilisée est le choix d'utiliser l'indexation à partir d'un pour les tableaux. Bien que je trouve cela un peu ennuyeux d'un point de vue pratique, cela ne rompt certainement pas l'accord, étant donné qu'il n'est pas unique à Julia (Matlab et Fortran utilisent également l'indexation en commençant par un).
Maintenant, pour l'aspect bon et le plus important: Julia peut vraiment être très rapide. J'ai été impressionné de voir comment le code Julia que j'ai écrit pour cet article peut mieux fonctionner que le code Fortran et C équivalent, même si je l'ai simplement traduit en Julia. Jetez un œil à la section performances si vous êtes intéressé.
2. Installation d'Open MPI
Open MPI est une bibliothèque d'interface de messagerie open source. D'autres bibliothèques bien connues incluent MPICH et MVAPICH. Développée par l'Ohio State University, MVAPICH est actuellement la bibliothèque la plus avancée car elle peut également prendre en charge les clusters GPU - ce qui est particulièrement utile pour les applications Deep Learning (en effet, il existe une étroite collaboration entre NVIDIA et l'équipe MVAPICH).
Toutes ces bibliothèques sont construites sur une interface commune: l'API MPI. Par conséquent, peu importe si vous utilisez l'une ou l'autre bibliothèque: le code que vous avez écrit peut rester le même.
Le projet MPI.jl sur Github est un wrapper pour MPI. Sous le capot, il utilise les installations C et Fortran MPI. Cela fonctionne très bien, bien qu'il manque certaines des fonctionnalités disponibles dans ces autres langues.
Pour exécuter MPI sur Julia, vous devrez installer Open MPI séparément sur votre ordinateur. Si vous avez un Mac, j'ai trouvé ce guide très utile. Il est important de noter que vous devrez également installer gcc (le compilateur GNU), car Open MPI nécessite les compilateurs Fortran et C. J'ai installé la version d'Open MPI 3.1.1, qui est également confirmée par mpiexec --version sur mon terminal.
Une fois Open MPI installé sur votre ordinateur, vous devez installer cmake . Encore une fois, si vous avez un Mac, c'est aussi simple que de taper brew install cmake sur votre terminal.
Pour le moment, vous êtes prêt à installer le package MPI dans Julia. Ouvrez Julia REPL et tapez à l' using Pkg Pkg.add («MPI») . Habituellement, à ce stade, vous devriez pouvoir importer le package à l'aide de MPI pour importer. Cependant, j'ai également dû construire le package via Pkg.build («MPI») avant que cela fonctionne.
3. Problème: équation de diffusion bidimensionnelle
L'équation de diffusion est un exemple d'équation différentielle partielle parabolique. Il décrit des phénomènes tels que la diffusion de chaleur ou la diffusion de concentration (deuxième loi de Fick). En deux dimensions spatiales, l'équation de diffusion s'écrit
Solution montre comment la température / concentration change (selon que l'on étudie la distribution de chaleur ou la diffusion de substances) dans l'espace et le temps. En effet, les variables x et y représentent les coordonnées spatiales, et la composante temporelle est représentée par la variable t . La quantité D est le «coefficient de diffusion» et détermine à quelle vitesse, par exemple, la chaleur se propage à travers la région physique. Semblable à ce qui a été discuté (plus en détail) dans un article de blog précédent, l'équation ci-dessus peut être discrétisée en utilisant le soi-disant «schéma explicite» de la solution. Je n'entrerai pas dans les détails que vous pouvez trouver sur le blog, écrivez simplement une solution numérique sous la forme suivante:
où i et k indices parcourant la grille spatiale, j dans le temps. La première couche de temps est remplie à partir des conditions initiales et chaque calculé en utilisant les valeurs de la couche précédente. Sur la figure, les nœuds rouges indiquent les nœuds de la couche qui sont nécessaires pour calculer la valeur au point

L'équation (1) est vraiment tout ce qui est nécessaire pour trouver une solution sur toute la zone à chaque pas de temps suivant. Il est assez simple d'implémenter du code qui le fait de manière séquentielle avec un processus sur le CPU. Cependant, ici, nous voulons discuter d'une implémentation parallèle qui utilise plusieurs processus.
Chaque processus sera chargé de trouver une solution dans une partie de l'ensemble du domaine spatial. Des problèmes tels que la diffusion de la chaleur, qui ne sont pas des candidats évidents pour l'informatique distribuée, nécessitent l'échange d'informations entre les processus. Pour clarifier ce point, regardons l'image
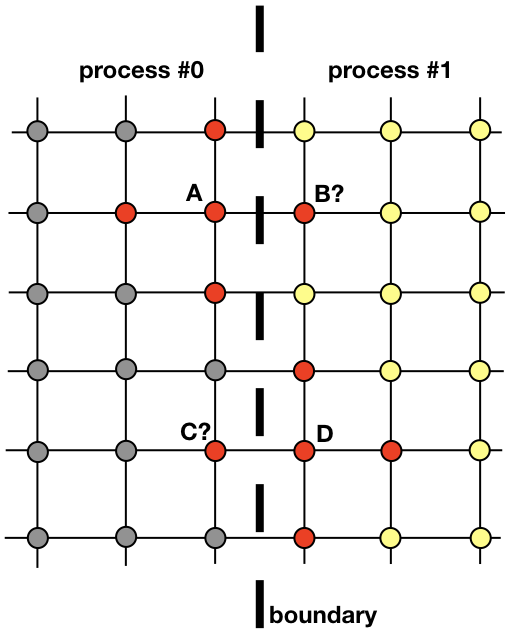
Deux processus voisins doivent interagir pour trouver une solution près de la frontière. Le processus 0 doit connaître la valeur de la solution en B pour calculer la solution au point de grille A. De même, le processus 1 doit connaître la valeur au point C pour calculer la solution au point de grille D. Ces valeurs sont inconnues des processus jusqu'à ce qu'il y ait une connexion entre les processus 0 et 1 .
Il montre comment les processus 0 et 1 devront interagir pour évaluer une solution près de la frontière. C'est là que MPI entre en scène. Dans la section suivante, nous examinerons un moyen efficace de messagerie.
4. Communication entre processus: cellules fantômes
Un concept important dans la dynamique des fluides de calcul est le concept de cellules fantômes. Ce concept est utile chaque fois qu'un domaine spatial est décomposé en plusieurs sous-domaines, chacun étant résolu par un seul processus.
Pour comprendre ce que sont les cellules fantômes, regardons à nouveau deux zones voisines dans l'image précédente. Le processus 0 est chargé de trouver la solution sur le côté gauche, tandis que le processus 1 la trouve sur le côté droit du domaine spatial. Cependant, en raison de la forme du pochoir (Fig. 2) près de la bordure, les deux processus devront échanger des données. Voici le problème: il est très inefficace que le processus 0 et le processus 1 communiquent chaque fois qu'ils ont besoin d'un nœud d'un processus voisin: cela entraînerait des coûts de communication inacceptables.
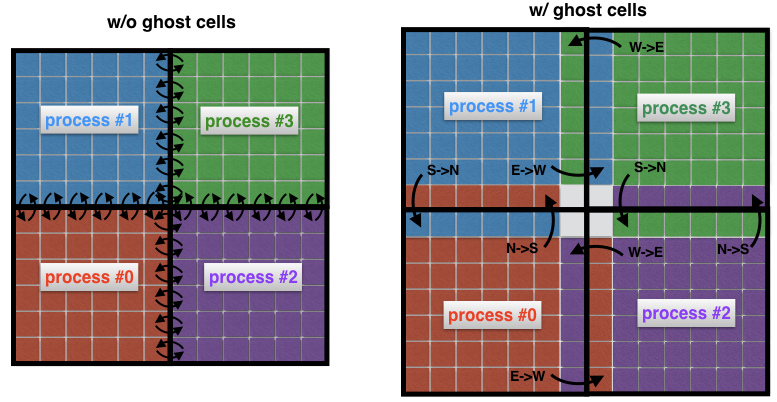
Fig. 4 Connexion entre processus sans (à gauche) et avec (à droite) cellules fantômes. Sans cellules intermédiaires, chaque cellule à la frontière d'un sous-domaine doit transmettre son propre message à un processus voisin. L'utilisation de cellules fantômes vous permet de minimiser le nombre de messages transmis, car de nombreuses cellules appartenant aux limites du processus échangent un message à la fois. Ici, par exemple, le processus 0 transfère toute la frontière nord au processus 1, et toute la frontière orientale au processus 2.
Au lieu de cela, il est courant d'entourer les sous-domaines «réels» de cellules supplémentaires appelées cellules fantômes, comme le montre la figure 4 (à droite). Ces cellules fantômes sont des copies de la solution aux frontières des sous-domaines voisins. À chaque pas de temps, l'ancienne limite de chaque sous-domaine est transmise aux voisins. Cela vous permet de calculer une nouvelle solution à la frontière d'un sous-domaine avec une surcharge de communication considérablement réduite. L'effet net est l'accélération du code.
5. Utilisation de MPI
Il existe de nombreux didacticiels MPI. Ici, je veux juste décrire les commandes exprimées dans le langage shell MPI.jl pour Julia que j'ai utilisées pour résoudre le problème de diffusion bidimensionnelle. Ce sont quelques commandes de base qui sont utilisées dans presque toutes les implémentations MPI.
Commandes MPIMPI.init () - initialise le runtime
MPI.COMM_WORLD - représente le communicateur, c'est-à-dire tous les processus disponibles via l'application MPI (chaque message doit être associé au communicateur)
MPI.Comm_rank (MPI. COMM_WORLD) - définit le rang interne (id) du processus
MPI.Barrier (MPI.COMM_WORLD) - bloque l'exécution jusqu'à ce que tous les processus aient atteint cette procédure
MPI.Bcast! (Buf, n_buf, rank_root, MPI.COMM_WORLD) MPI.Bcast! (Buf, n_buf, rank_root, MPI.COMM_WORLD) - diffusion du tampon de messages buf de taille n_buf à partir d'un processus de rang rank_root vers tous les autres processus du communicateur MPI.COMM_WORLD
MPI.Waitall! (reqs) MPI.Waitall! (reqs) - attend la fin de toutes les requêtes MPI (la requête est un descripteur, en d'autres termes, un lien, pour le transfert de message asynchrone)
MPI.REQUEST_NULL - indique que la demande n'est associée à aucune connexion en cours
MPI.Gather (buf, rank_root, MPI.COMM_WORLD) - réduit la variable buf au processus d'obtention de rank_root
MPI.Isend (buf, rank_dest, tag, MPI.COMM_WORL D) - le message buf est envoyé de manière asynchrone du processus en cours au processus rank_dest et le message est marqué avec le paramètre
MPI.Irecv! (Buf, rank_src, tag, MPI.COMM_WORLD) MPI.Irecv! (Buf, rank_src, tag, MPI.COMM_WORLD) - reçoit un message avec la balise tag du processus de classement rank_src d'origine vers le tampon buf local
MPI.Finalize () - termine le runtime MPI
5.1 Recherche de voisins de processus
Pour notre tâche, nous allons décomposer notre région bidimensionnelle en plusieurs sous-domaines rectangulaires, comme le montre la figure ci-dessous.

Figure 5. Décomposition cartésienne d'une région bidimensionnelle divisée en 12 sous-domaines. Notez que les classements MPI (identificateurs de processus) commencent à zéro.
Notez que les axes x et y sont inversés par rapport à une utilisation normale pour associer l'axe x aux lignes et l'axe y aux colonnes de la matrice de solution.
Pour communiquer entre différents processus, chaque processus doit connaître ses voisins. Il existe une commande MPI très pratique qui le fait automatiquement et s'appelle MPI_Cart_create . Malheureusement, le shell Julia MPI n'inclut pas cette commande avancée (et l'ajouter ne semble pas anodin), j'ai donc décidé de créer une fonction qui effectue la même tâche. Pour le rendre plus compact, j'ai souvent utilisé l' opérateur ternaire . Vous pouvez trouver cette fonction ci-dessous.
Code function neighbors(my_id::Int, nproc::Int, nx_domains::Int, ny_domains::Int) id_pos = Array{Int,2}(undef, nx_domains, ny_domains) for id = 0:nproc-1 n_row = (id+1) % nx_domains > 0 ? (id+1) % nx_domains : nx_domains n_col = ceil(Int, (id + 1) / nx_domains) if (id == my_id) global my_row = n_row global my_col = n_col end id_pos[n_row, n_col] = id end neighbor_N = my_row + 1 <= nx_domains ? my_row + 1 : -1 neighbor_S = my_row - 1 > 0 ? my_row - 1 : -1 neighbor_E = my_col + 1 <= ny_domains ? my_col + 1 : -1 neighbor_W = my_col - 1 > 0 ? my_col - 1 : -1 neighbors = Dict{String,Int}() neighbors["N"] = neighbor_N >= 0 ? id_pos[neighbor_N, my_col] : -1 neighbors["S"] = neighbor_S >= 0 ? id_pos[neighbor_S, my_col] : -1 neighbors["E"] = neighbor_E >= 0 ? id_pos[my_row, neighbor_E] : -1 neighbors["W"] = neighbor_W >= 0 ? id_pos[my_row, neighbor_W] : -1 return neighbors end
Nous avons fait de même lorsque nous avons construit des labyrinthes
L'entrée de cette fonction est my_id , qui est le rang (ou identifiant) du processus, le nombre de processus nproc , le nombre de divisions dans la direction x nx_domains et le nombre de divisions dans la direction y ny_domains .
Vérifions cette fonctionnalité maintenant. Par exemple, en regardant à nouveau la fig. 5, nous pouvons vérifier la sortie pour le processus de rang 4 et le processus de rang 11. Passons en REPL:
julia> neighbors(4, 12, 3, 4) Dict{String,Int64} with 4 entries: "S" => 3 "W" => 1 "N" => 5 "E" => 7
et
julia> neighbors(11, 12, 3, 4) Dict{String,Int64} with 4 entries: "S" => 10 "W" => 8 "N" => -1 "E" => -1
Comme vous pouvez le voir, j'utilise les directions cardinales "N", "S", "E", "W" pour indiquer l'emplacement d'un voisin. Par exemple, le processus 4 a le processus 3 comme voisin situé au sud de sa position. Vous pouvez vérifier que tous les résultats ci-dessus sont corrects, étant donné que «-1» dans le deuxième exemple signifie qu'aucun voisin n'a été trouvé sur les côtés «nord» et «est» du processus 11.
5.2 Messagerie
Comme nous l'avons vu précédemment, à chaque itération, chaque processus envoie ses frontières aux processus voisins. Dans le même temps, chaque processus reçoit des données de ses voisins. Ces données sont stockées par chaque processus sous la forme de "cellules fantômes" et sont utilisées pour calculer la solution près de la limite de chaque sous-domaine.
MPI possède une commande MPI_Sendrecv très utile qui vous permet d'envoyer et de recevoir des messages simultanément entre deux processus. Malheureusement, MPI.jl ne fournit pas cette fonctionnalité, mais il est toujours possible d'obtenir le même résultat en utilisant les fonctions MPI_Send et MPI_Receive séparément.
Voici ce qui a été fait dans la prochaine fonction updateBound! , qui met à jour les cellules fantômes à chaque itération. L'entrée de cette fonction est une solution 2D globale u, qui comprend des cellules fantômes, ainsi que toutes les informations liées à un processus spécifique qui exécute une fonction (quel est son rang, quelles sont les coordonnées de son sous-domaine, quels sont ses voisins). La fonction envoie d'abord ses frontières aux voisins, puis reçoit leurs frontières. La réception est en cours de finalisation par l'équipe MPI.Waitall! , ce qui garantit que tous les messages attendus ont été reçus avant de mettre à jour les cellules latérales pour un sous-domaine d'intérêt particulier.
Code function updateBound!(u::Array{Float64,2}, size_total_x, size_total_y, neighbors, comm, me, xs, ys, xe, ye, xcell, ycell, nproc) mep1 = me + 1
5. Visualisation de la solution
Le domaine est initialisé avec une valeur constante u = +10 autour de la frontière, ce qui peut être interprété comme la présence d'une source de température constante à la frontière. La condition initiale u = −10 à l'intérieur de la région (Fig. 6 à gauche). Au fil du temps, la valeur u = 10 à la frontière diffuse au centre de la région. Par exemple, à l'étape j = 15203 solution ressemble à celle montrée sur la Fig. 6 à droite.
Avec l'augmentation du temps t, la solution devient de plus en plus homogène, alors que théoriquement pour il ne deviendra pas u = +10 dans tout le domaine.

Fig. 6. La condition initiale (à gauche) et la solution à l'étape 15203 dans le temps (à droite). Les limites de la région sont toujours stockées à u = +10. Au fil du temps, la solution devient de plus en plus uniforme et tend à se rapprocher de plus en plus de la valeur u = +10 dans toute la région.
6. Performance
J'ai été très impressionné lorsque j'ai testé les performances de l'implémentation Julia par rapport à Fortran et C: j'ai trouvé que l'implémentation Julia est la plus rapide!
Avant de plonger dans la comparaison, regardons les performances MPI du code Julia lui-même. La figure 7 montre le ratio d'exécution lors de l'utilisation des processus 1 à 2 (CPU). Idéalement, vous souhaitez que ce nombre soit proche de 2, c'est-à-dire travailler avec deux processeurs devrait être deux fois plus rapide qu'avec un seul processeur. Au lieu de cela, on observe que pour les petites tailles de tâches (une grille de 128 x 128 cellules), le temps de compilation et les frais généraux de communication ont un impact négatif sur le temps d'exécution global: l'accélération est inférieure à un. L'avantage d'utiliser plusieurs processus n'apparaît que pour des tâches plus importantes.
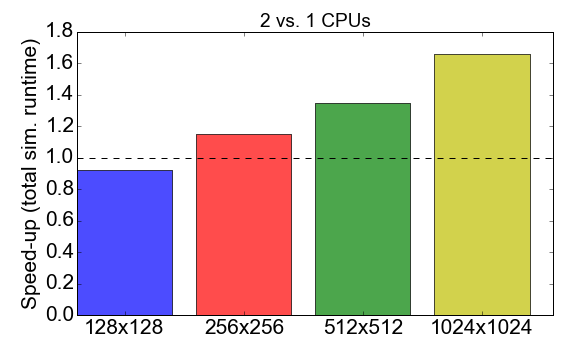
Figure 7. Accélération de l'implémentation de Julia MPI avec deux processus par rapport à un processus, selon la complexité de la tâche (taille de la grille). «Accélération» fait référence au rapport entre le temps d'exécution total utilisant 1 processus et 2 processus.
Et maintenant un tournant inattendu: sur la fig. La figure 8 montre que l'implémentation de Julia est plus rapide que Fortran et C pour les tâches de taille 256x256 et 512x512 (uniquement celles que j'ai testées). Ici, je mesure uniquement le temps nécessaire pour terminer la boucle d'itération principale. Je pense que c'est une comparaison juste, car pour les longues simulations, ce sera la plus grande contribution à l'exécution globale.
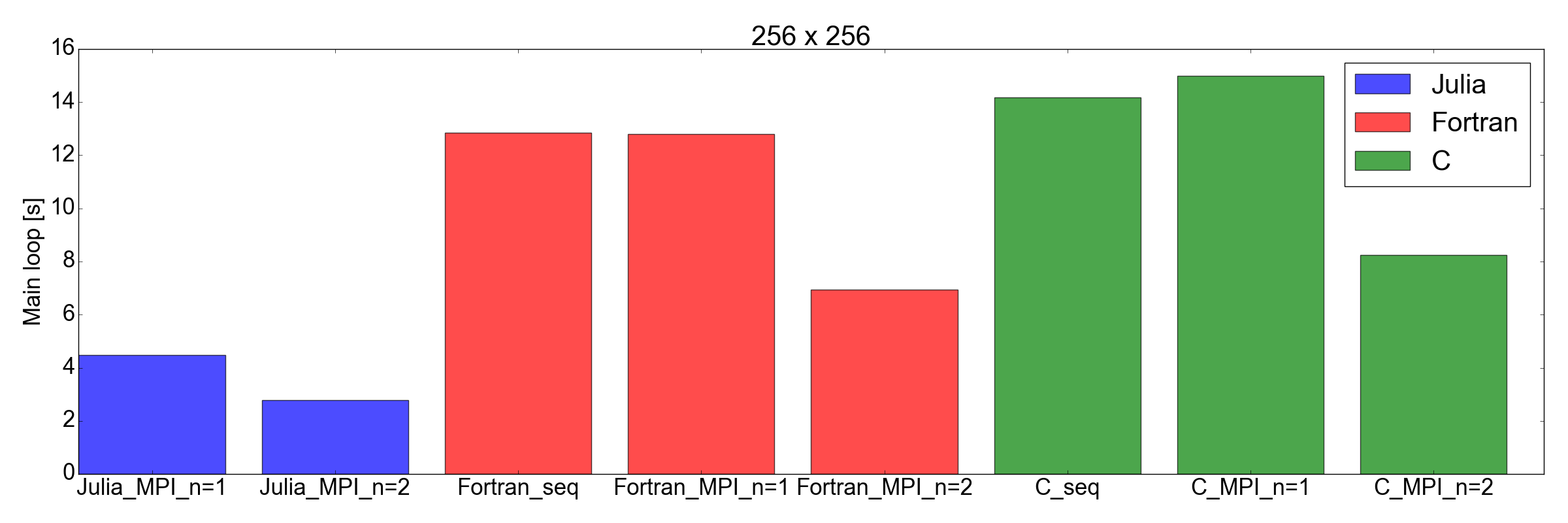

Figure 8. Performances de Julia vs Fortran vs C pour deux tailles de grille: 256x256 (en haut) et 512x512 (en bas). Cela montre que Julia est la langue la plus performante. Les performances sont mesurées comme le temps nécessaire pour effectuer un nombre fixe d'itérations dans la boucle de code principale.
Conclusions
Avant de commencer ce poste, j'étais sceptique quant au fait que Julia pouvait rivaliser avec la vitesse de Fortran et C pour des applications scientifiques. La principale raison était que j'avais précédemment traduit le code académique contenant environ 2000 lignes de Fortran en Julia 0.6, et j'ai remarqué une baisse de performance d'environ 3 fois.
Mais cette fois ... je suis très impressionnée. En fait, je viens de traduire l'implémentation MPI existante écrite en Fortran et C en Julia 1.0. Les résultats montrés sur la fig. 8, parlent d'eux-mêmes: Julia semble être la plus rapide à ce jour. Veuillez noter que je n'ai pas pris en compte le long temps de compilation consommé par le compilateur Julia, car ce sera un facteur insignifiant pour les "vraies" applications qui nécessitent des heures pour se terminer.
Je dois également ajouter que mes tests ne sont bien sûr pas aussi complets qu'ils devraient l'être pour une comparaison approfondie. En fait, je serais curieux de voir comment le code fonctionne avec plus de deux processeurs (je suis limité à mon ordinateur portable personnel) et avec d'autres équipements (voir Diffusion.jl ).
Quoi qu'il en soit, cet exercice m'a convaincu qu'il valait la peine de passer plus de temps à étudier et à utiliser Julia pour la science des données et les applications scientifiques. Accédez à de nouvelles réalisations!
Les références