Bonjour, Habr!
En tant que
législateurs sur
Unity sur le marché russe, nous vous proposons de lire une étude intéressante sur l'utilisation pratique de l'algorithme WFC (Wave Function Collapse), construit à l'image et à la ressemblance du principe bien connu de la mécanique quantique et très pratique pour la génération procédurale de niveaux dans les jeux. Plus tôt dans Habré, l'
histoire détaillée de cet algorithme a déjà été publiée. L'auteur de l'article d'aujourd'hui, Marian Kleineberg, considère l'algorithme dans le contexte des graphiques en trois dimensions et de la génération d'une ville sans fin. Bonne lecture!
Nous allons parler d'un jeu où vous vous promenez dans une ville sans fin qui est générée de manière procédurale lorsque vous vous déplacez. Une ville est construite à partir d'un ensemble de blocs en utilisant l'algorithme WFC (effondrement de la fonction d'onde).
L'assemblage jouable est disponible en téléchargement sur le site Web
itch.io. Vous pouvez également prendre le
code source sur github . Enfin, je propose une
vidéo dans laquelle je parcours la ville ainsi générée.
Algorithme
J'appellerai le mot «cellule» un élément maillé de voxel 3D qui peut contenir un bloc ou être vide. Le mot "module" j'appellerai un bloc qui peut occuper une telle cellule.
L'algorithme décide des modules à sélectionner dans chaque cellule du monde du jeu. Un tableau de cellules est considéré comme une fonction d'onde sous une forme non observable. Ainsi, chaque cellule correspond à de nombreux modules qui peuvent y apparaître. En termes de mécanique quantique, on pourrait dire, "la cellule est en superposition de tous les modules". L'existence du monde commence sous une forme complètement inobservable, où n'importe quel module peut être dans chaque cellule. De plus, toutes les cellules s'effondrent l'une après l'autre. Cela signifie que pour chaque cellule, un module est sélectionné au hasard parmi tous les possibles.
L'étape suivante est la propagation des contraintes. Pour chaque module, un sous-ensemble de modules est sélectionné et peut être adjacent à celui-ci. Chaque fois qu'un module s'effondre, des sous-ensembles d'autres modules sont mis à jour, qui sont toujours autorisés comme adjacents à celui-ci. L'étape de propagation des restrictions est la partie de l'algorithme la plus consommatrice de ressources en termes de puissance de calcul.
Un aspect important de l'algorithme consiste à déterminer la cellule à effondrer. L'algorithme réduit toujours la cellule avec la
plus petite entropie . Il s'agit d'une cellule qui permet un nombre minimal de choix (c'est-à-dire une cellule avec le moins d'aléatoire). Si la probabilité d'effondrement est la même pour tous les modules, alors la cellule avec le nombre minimum de modules possibles aura l'entropie la plus faible. En règle générale, les probabilités d'être sélectionnées sont différentes pour les différents modules disponibles. Une cellule avec deux modules possibles ayant la même probabilité offre un choix plus large (entropie supérieure) que celui dans lequel il y a deux modules, et pour l'un d'eux la probabilité de tomber sous le choix est très élevée, et pour l'autre elle est très petite.

(Gif publié par
ExUtumno sur Github)
Des informations plus détaillées sur l'algorithme d'effondrement de la fonction d'onde, ainsi qu'un certain nombre de beaux exemples, peuvent être trouvés ici. Initialement, cet algorithme a été proposé pour générer des textures 2D basées sur un seul échantillon. Dans ce cas, les indicateurs probabilistes des modules et les règles d'adjacence sont déterminés en fonction de leur occurrence dans l'exemple. Cet article fournit ces informations manuellement.
Voici une
vidéo démontrant cet algorithme en action.
À propos des blocs, prototypes et modules
Le monde est généré à partir d'un ensemble dans lequel environ 100 blocs. Je les ai créés en utilisant Blender. Au début, j'avais très peu de blocs, et je les ai ajoutés petit à petit quand je l'ai jugé nécessaire.

L'algorithme doit savoir quels modules peuvent être placés côte à côte. Pour chaque module, il y a 6 listes de voisins possibles, une dans chacune des directions. Cependant, je voulais éviter d'avoir à créer une telle liste manuellement. De plus, je voulais générer automatiquement des options tournées pour chacun de mes blocs.
Ces deux tâches sont résolues à l'aide des modules dits prototypes. Il s'agit essentiellement de
MonoBehaviour , qui est pratique pour travailler avec l'éditeur Unity. Des modules ainsi que des listes d'éléments voisins valides et des options pivotées sont automatiquement créés sur la base de ces prototypes.
Un problème complexe s'est posé avec la modélisation des informations d'adjacence, de sorte que ce processus automatique a fonctionné. Voici ce que j'ai obtenu:

Chaque bloc a 6 contacts, un pour chaque face. Le contact a un numéro. De plus, les contacts horizontaux peuvent être inversés, non inversés ou symétriques. Les contacts verticaux ont soit un indice de rotation compris entre 0 et 3, soit sont marqués comme
invariants en rotation .
Sur cette base, je peux vérifier automatiquement quels modules sont autorisés à s'emboîter. Les modules adjacents doivent avoir les mêmes numéros de broche. Leur symétrie doit également coïncider (le même indice de rotation vertical, une paire de contacts horizontaux inversés et non inversés), ou les modules doivent être symétriques / invariants.
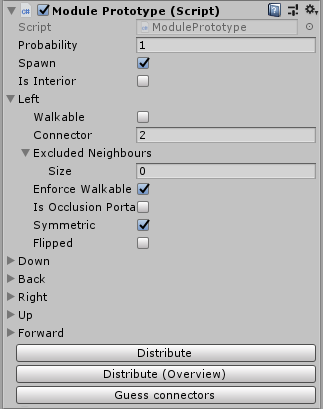
Il existe des règles d'exclusion par lesquelles je peux interdire les options de quartier qui seraient autorisées par défaut. Certains blocs avec des contacts correspondants semblent tout simplement laids à proximité. Voici un exemple de carte générée sans appliquer de règles d'exception:

Chemin vers l'infini
L'algorithme d'effondrement de la fonction d'onde d'origine génère des cartes de taille finie. Je voulais construire un monde qui se développera et se développera au fur et à mesure que vous avancerez.
Au début, j'ai essayé de générer des fragments de taille finie et d'utiliser les contacts des fragments adjacents comme restrictions. Si un fragment est généré et qu'un fragment adjacent à celui-ci est également généré, seuls les modules de ce type sont autorisés à côté des modules existants. Avec cette approche, le problème suivant se pose: chaque fois qu'une cellule s'effondre, la propagation des restrictions réduira les opportunités même à une distance de plusieurs cellules. L'image suivante montre les effets de l'effondrement d'une seule cellule:

Si à chaque étape de l'algorithme un seul fragment est généré, les restrictions ne s'appliquent pas aux fragments adjacents. Dans ce cas, de tels modules ont été sélectionnés à l'intérieur du fragment, ce qui serait inacceptable si d'autres fragments étaient pris en compte. Par conséquent, lorsque l'algorithme a tenté de générer le fragment suivant, il n'a pas pu trouver une seule solution.
Maintenant, je n'utilise plus de fragments, mais stocke la carte dans un dictionnaire qui affiche la position d'une cellule sur une cellule. La cellule n'est remplie que si nécessaire. Certains éléments de l'algorithme doivent être ajustés dans cet esprit. Lors du choix d'une cellule qui doit s'effondrer, il est impossible de prendre en compte toutes les cellules si leur nombre est infini. Au lieu de cela, nous ne générons qu'une petite partie de la carte à la fois, une fois que le joueur l'a atteinte. En dehors de cette zone, les restrictions continuent de se propager.
Dans certains cas, cette approche ne fonctionne pas. Considérez un ensemble de modules pour une section droite d'un tunnel de la figure ci-dessus - il n'y a pas d'entrée dans le tunnel. Si l'algorithme choisit un tel module de tunnel, alors le tunnel sera infini par définition. Au stade de la distribution des restrictions, le programme tentera d'allouer un nombre infini de cellules. J'ai développé un ensemble spécial de modules pour contourner ce problème.
Conditions aux limites
Il existe deux conditions aux limites importantes. Tous les visages au niveau supérieur de la carte doivent avoir des contacts «aériens». Tous les visages sur la base de la carte doivent avoir des contacts «solides». Si ces conditions ne sont pas remplies, sur la carte, il y aura des trous dans le sol et certains bâtiments seront sans toit.
Sur une carte de taille finie, ce problème serait facilement résolu. Pour toutes les cellules au niveau le plus élevé et le plus bas, il serait nécessaire de retirer tous les modules avec des contacts inappropriés. Commencez ensuite la distribution des restrictions et supprimez les modules restants qui ne nous conviennent plus.
Sur une carte de taille infinie, cela ne fonctionnera pas, car au plus haut et au plus bas niveau, nous avons un nombre infini de cellules. La solution la plus naïve consiste à supprimer toutes les cellules inappropriées dès qu'elles apparaissent. Cependant, lorsqu'un module est supprimé au niveau supérieur, des restrictions s'appliquent aux cellules qui lui sont adjacentes. Il y a un effet d'avalanche, conduisant à nouveau à une sélection infinie de cellules.
J'ai résolu ce problème en créant une carte 1 × n × 1, où n est la hauteur. Cette carte utilise l'habillage du monde pour répartir les restrictions. Le mécanisme fonctionne comme dans le jeu Pacman: en dépassant le bord droit de la carte, le personnage y revient à cause du bord gauche. Maintenant, je peux appliquer toutes les restrictions à ma carte. Chaque fois que vous créez une nouvelle cellule sur une carte infinie, cette cellule est initialisée avec un ensemble de modules correspondant à une position spécifique sur la carte.
Conditions d'erreur et recherche de retour
Parfois, l'algorithme WFC atteint un état dans lequel la cellule ne correspond à aucun module possible. Dans les applications où nous avons affaire à un monde de taille finie, vous pouvez simplement réinitialiser le résultat et recommencer à zéro. Dans un monde infini, cela ne fonctionnera pas, car une partie du monde est déjà montrée au joueur. Tout d'abord, j'ai opté pour une solution dans laquelle les endroits où les erreurs se sont produites étaient remplis de blocs blancs.
J'utilise actuellement la recherche de retour. L'ordre de l'effondrement des cellules et certaines informations sur la répartition des restrictions sont stockées sous forme d'historique. Si l'algorithme WFC échoue, une partie de l'historique est annulée. En règle générale, cela fonctionne, mais parfois des erreurs peuvent être détectées trop tard, et une recherche de retour couvre de nombreuses étapes. Dans de rares cas, la cellule dans laquelle se trouve le joueur est régénérée.
À mon avis, en raison de cette limitation, l'application de l'algorithme WFC avec des mondes infinis ne convient pas aux jeux commerciaux.
Contexte
J'ai commencé à travailler sur cette tâche après avoir regardé une
conférence d'Oscar Stelberg racontant comment il utilise l'algorithme pour générer des niveaux dans le jeu Bad North. En général, mon algorithme a été implémenté pendant la semaine de
procjam .
J'ai quelques idées pour affiner encore cet algorithme, mais je ne suis pas sûr qu'un jour je vais y ajouter du gameplay. Et si je me réunis - ce ne sera certainement pas une stratégie aussi épique que vous l'avez déjà imaginée. Cependant, si vous voulez vérifier comment vos mécanismes de jeu préférés fonctionnent avec cet algorithme - essayez-le vous-même! En fin de compte, le code source est accessible au public et autorisé par le MIT.