🕒 👍🏾 🎣 Talent contre chance: le rôle du hasard dans le succès et l'échec 👵🏼 ⬛️ 💔

Récemment, je suis tombé sur un travail intéressant de scientifiques italiens sur le rôle grandement sous-estimé de la chance et du hasard dans nos vies. Malheureusement, je n'ai pas trouvé la version complète en russe (peut-être que je regardais mal?), Mais je voulais vraiment partager ce que j'ai lu avec mes camarades anglais non fluides. Par conséquent, retroussant ses manches, il entreprit sa traduction artisanale. Les auteurs, Alessandro, Alessio et Andrea, ont aimablement autorisé à le publier dans le domaine public, donc si vous êtes intéressé, bienvenue sur cat.

Les auteurs

A. Pluchino - Département de physique et d'astronomie, Université de Catane et branche de Catane de l'Institut national de physique nucléaire, Italie; alessandro.pluchino@ct.infn.it
A. E. Biondo - Département d'économie et des affaires, Université de Catane, Italie; ae.biondo@unict.it
A. Rapisard - Département de physique et d'astronomie, Université de Catane et branche de Catane de l'Institut national de physique nucléaire, Italie; Centre pour l'étude des systèmes complexes, Vienne; andrea.rapisarda@ct.infn.it

Annotation

Dans une large mesure, le méritocratique dominant (la méritocratie est le principe de gestion, selon lequel les personnes les plus capables, indépendamment de leur origine sociale et de leur richesse financière ) occupent des postes de direction, le modèle des cultures occidentales hautement compétitif, provient de la conviction que le succès est principalement, sinon complètement, le succès. dépend de qualités personnelles telles que le talent, l'intelligence, les compétences, l'ingéniosité, le travail acharné, la persévérance, le travail acharné ou la prise de risques. Parfois, nous sommes prêts à admettre qu'une certaine part de chance peut également jouer un rôle dans la réussite matérielle significative. Mais, en vérité, l'importance des forces externes dans les réussites individuelles est souvent sous-estimée. Il est bien connu que l'intelligence (ou, généralement, le talent et les qualités personnelles) dans une population a une distribution gaussienne, tandis que la distribution des valeurs - souvent considérée comme une mesure du succès - suit généralement une loi de puissance (loi de Pareto) lorsque la majorité est pauvre et il y a un nombre négligeable de milliardaires. Cet écart entre des entrées normalement distribuées qui ont un niveau normal (talent ou intelligence moyenne) et une distribution constante à la sortie suggère qu'il y a quelque part dans les coulisses une composante invisible. Dans cet article, sur la base d'une simulation extrêmement simple et basée sur un agent jouet, nous faisons l'hypothèse qu'un tel composant est un accident ordinaire. En particulier, nous montrons que, si le succès dans la vie requiert vraiment une certaine quantité de talent, les personnes les plus douées n'atteignent presque jamais les plus hauts sommets de richesse, dépassées par des personnalités médiocres mais beaucoup plus prospères. À notre connaissance, ce résultat contradictoire de bon sens - bien qu'implicitement supposé entre les lignes dans de nombreuses publications - a été le premier à donner une évaluation quantitative. Cela vous permet de jeter un regard neuf sur l'efficacité de l'évaluation des mérites sur la base d'un niveau de réussite déjà atteint et souligne les risques de répandre des honneurs ou des ressources excessifs auprès de personnes qui, à long terme, pourraient bien être plus efficaces que d'autres. En utilisant ce modèle, nous considérons et comparons également plusieurs hypothèses comportementales pour montrer les stratégies les plus efficaces pour le financement public de la recherche, dans le but d'améliorer la méritocratie, la diversité et l'innovation.

1. Introduction

L'omniprésence de la dépendance au pouvoir dans de nombreux systèmes complexes physiques, biologiques ou socio-économiques peut être considérée comme quelque chose comme une caractéristique mathématique distincte de la relation étroite de leurs caractéristiques dynamiques avec une structure topologique inchangée à l'échelle [1, 2, 3, 4]. Dans le contexte socio-économique, selon les travaux de Pareto [5, 6, 7, 8, 9], il est bien connu que la répartition des richesses a un caractère de loi de puissance, dont la forme allongée caractéristique reflète la profondeur de l'abîme existant entre les riches et les pauvres de notre société.

Un récent rapport [10] montre qu'aujourd'hui cet écart est beaucoup plus important que nous le craignions: huit personnes possèdent la même richesse que 3,6 milliards de personnes, qui constituent la partie la plus pauvre de l'humanité. Au cours des 20 dernières années, plusieurs modèles théoriques ont été développés pour calculer la distribution des valeurs dans le contexte de la théorie des probabilités et des statistiques physiques, prenant souvent la forme d'une modélisation multi-agents avec une dynamique interne simple [11, 12, 13, 14, 15, 16, 17].

En allant plus loin dans cette direction, si nous considérons la richesse personnelle comme une mesure du succès, on peut affirmer que la répartition profondément asymétrique et inégale entre les personnes est la conséquence de leurs différences naturelles de talent, de compétences, de compétence, d'intelligence, de capacités ou la mesure de leur persévérance, de dur labeur ou détermination. Une telle hypothèse, sous une forme implicite, est à la base du soi-disant paradigme méritocratique: elle affecte non seulement la façon dont notre société offre des opportunités d'emploi, d'honneur et de renommée, mais aussi les stratégies adoptées par les gouvernements pour allouer des ressources et des financements à ceux qui sont considérés comme les plus personnalités honorées.

Cependant, la conclusion précédente semble être très différente des données confirmées selon lesquelles les propriétés et les qualités des personnes susmentionnées sont normalement réparties dans la population, c'est-à-dire qu'elles correspondent à une distribution gaussienne symétrique par rapport à cette moyenne. Par exemple, l'intelligence, telle que mesurée par les tests de QI, correspond au modèle suivant: le QI moyen est de 100, mais personne n'a un QI de 1000 ou 10000. Il en va de même pour le travail compté en heures de travail: quelqu'un travaille plus que la moyenne, un autre moins, mais personne ne travaille un milliard d'heures de plus que les autres.

Mais à notre époque, il y a de plus en plus de preuves concernant le rôle fondamental du hasard, de la chance ou, en général, des facteurs aléatoires, pour déterminer le succès ou l'échec de nos affaires personnelles et professionnelles. En particulier, il a été démontré que tous les scientifiques ont la même chance de publier des travaux révolutionnaires au cours de leur carrière [18]; que ceux dont la première lettre du nom de famille se rapproche du début de l'alphabet sont beaucoup plus susceptibles de recevoir le poste de chef de département [19]; que les distributions d'indicateurs bibliométriques collectées par les scientifiques peuvent s'avérer aléatoires et dénuées de sens en raison du phénomène croissant associé au mécanisme inflationniste «publier ou mourir» [20]; que la position d'une personne dans une liste triée par ordre alphabétique peut être importante pour déterminer l'accès aux services publics limité par le nombre de places [21]; que la lettre initiale d'un deuxième prénom soulève une évaluation des capacités intellectuelles [22]; que les personnes dont le nom est facilement prononcé sont mieux notées que celles dont le nom est complexe [23]; que ceux dont les noms sonnent plus aristocratiques plus souvent que d'autres travaillent comme dirigeants et non comme subordonnés [24]; que les femmes portant des surnoms masculins réussissent mieux dans la profession juridique [25]; qu'environ la moitié des différences de revenus entre les personnes dans le monde s'expliquent uniquement par leur pays de résidence et la répartition des salaires dans le pays concerné [26]; que la probabilité de devenir administrateur est fortement influencée par votre nom et votre mois de naissance [27, 28, 29]; que les idées innovantes sont le résultat de réactions aléatoires dans les cellules de notre cerveau [30]; et que même la probabilité de développer un cancer, susceptible de détruire une excellente carrière, dépend en grande partie de l'échec [31, 32]. Des travaux récents sur le thème de la réussite de la reproduction tout au long de la vie contribuent à la confirmation de telles affirmations, montrant que si les écarts de traits peuvent affecter le sort de la population dans son ensemble, la vie d'individus spécifiques est souvent déterminée par la chance.

Ces dernières années, de nombreux auteurs, dont le statisticien et analyste des risques Nassim Taleb [35, 36], le stratège en investissements Michael Mobussin [37] et l'économiste Robert Frank [38], ont étudié dans un certain nombre de livres populaires le lien entre la chance et la compétence dans les transactions financières. affaires, sports, art, musique, littérature, science et bien d'autres domaines. Ils ont conclu que les événements aléatoires jouent un rôle beaucoup plus important dans la vie que beaucoup l'auraient imaginé. En fait, ils ne supposent pas que le succès ne dépend pas du talent et des efforts, car dans des domaines ou des marchés extrêmement compétitifs tels que «le gagnant prend tout», où nous vivons et travaillons en ce moment, les personnes les plus productives sont presque toujours extraordinaires talentueux et travailleur. Ils ont seulement conclu que le talent et l'effort ne suffisaient pas: vous devez également être au bon endroit au bon moment. En bref, la chance affecte également, bien que son rôle soit presque toujours sous-estimé par les gens qui réussissent. Cela est dû au fait que le hasard fonctionne souvent de manière non évidente, il est donc facile de comparer les événements qui montrent le succès comme quelque chose d'inévitable. Taleb appelle une telle inclination «une erreur fallacieuse fantastique» [36], et le sociologue Paul Lazarsfeld a proposé le terme «rétrospective biaisée». Dans son dernier livre, "Tout est évident: quand vous connaissez la réponse" [39], le sociologue et pionnier de la science des réseaux, Duncan Watts, suggère que l'illusion fabuleuse et la rétrospective biaisée font appel à un phénomène spécial dans lequel les gens qui voient des résultats exceptionnellement réussis, les considérer comme un produit indubitable de travail acharné et de talent. Cependant, le succès passe principalement par des étapes complexes et entrelacées, dont chacune dépend des précédentes: si l'une d'entre elles était différente, l'ensemble de la carrière ou du chemin de vie serait presque certainement également différent. Cet argument est également basé sur les résultats d'une étude expérimentale innovante menée plusieurs années auparavant par Watts lui-même en collaboration avec d'autres auteurs [40], dans laquelle le succès de chansons jusque-là inconnues sur le marché de la musique artificielle n'était pas en corrélation avec la qualité de l'œuvre elle-même. Et cela, bien sûr, complique grandement toute prédiction, comme le montre une autre étude plus récente [41].

Dans cet article, en utilisant une approche statistique basée sur les agents, nous allons essayer de déterminer pratiquement quantitativement le rôle de la chance et du talent dans des carrières réussies. Dans la section 2, sur la base du nombre minimal d'hypothèses, à savoir la nature gaussienne de la répartition des talents [42] et la dynamique multiplicative des succès et des échecs [43], nous présentons un modèle simple, que nous avons appelé le modèle «Talent vs Luck» (TPU), dans qui imite le développement des carrières professionnelles d'un groupe de personnes au cours de la période de 40 ans de leur travail. Le modèle montre qu'en réalité, le hasard joue un rôle fondamental dans la détermination des individus les plus performants. La vérité est que, comme on pourrait s'y attendre, les personnes talentueuses sont plus susceptibles de devenir riches, célèbres ou importantes dans leur propre vie, par rapport à des personnes moins préparées. Mais, et cette explication moins intuitive, les gens ordinaires avec un niveau de talent ordinaire sont statistiquement destinés à réussir (c'est-à-dire à se situer à la fin d'une certaine distribution de puissance du succès) beaucoup plus souvent que les plus talentueux, à condition qu'ils deviennent les favoris de la fortune pour de votre vie. Ce fait est souvent rencontré, comme indiqué dans les références [35, 36, 38], mais, à notre connaissance, il a d'abord été modélisé et mesuré dans ce travail.

Le succès des personnes au talent ordinaire remet en question le paradigme «méritocratique» et toutes ces stratégies et mécanismes qui ont donné plus de récompenses, d'opportunités, d'honneur, de renommée et de ressources à des personnes considérées comme les meilleures dans leur domaine [44, 45]. Le fait est que, dans la grande majorité des cas, toutes les évaluations du talent d'une personne ont été effectuées après coup, uniquement en examinant son activité ou les résultats obtenus, dans un domaine spécifique de notre société, comme le sport, les affaires, la finance, l'art. , science, etc. Ce type d'évaluation trompeuse conduit à une substitution de cause à effet, évaluant comme les personnes les plus talentueuses celles qui sont, tout simplement, les plus performantes [46, 47]. Conformément à ce point de vue, les travaux précédents ont mis en garde contre des types similaires de «quasi-méritocratie» et ont montré l'efficacité d'autres stratégies basées sur des échantillons aléatoires dans de nombreux environnements différents, tels que la gestion, la politique et les finances [48, 49, 50, 51, 52, 53, 54, 55]. Dans la section 3, nous appliquons notre approche et décrivons comment la distribution des fonds publics est possible dans le contexte de la recherche scientifique. Nous étudions les conséquences de diverses stratégies de distribution, parmi lesquelles une «quasi» méritocratique, dans le but d'explorer de nouvelles façons d'augmenter, en même temps, le niveau minimum de réussite des personnes les plus talentueuses de la société et l'efficacité totale des dépenses publiques. Nous examinerons également, en général, en quoi les opportunités offertes par l'environnement, présentées sous forme d'éducation et de niveaux de revenu (c'est-à-dire des facteurs externes selon le pays et la couche sociale dont les gens viennent), sont importantes pour augmenter les chances de succès. Des remarques finales complètent le travail.

2. Modèle

De plus, nous proposons un modèle d'agent appelé «Talent against Luck» (TPU), basé sur un petit nombre d'hypothèses, et visant à décrire l'évolution des carrières d'un groupe de personnes sous l'influence d'événements aléatoires réussis et infructueux.

Figure 1: Un exemple des paramètres initiaux de notre simulation. Toutes les simulations présentées dans cet article ont été réalisées dans l'environnement de simulation d'agent NetLogo [56]. N = 1000 personnes (agents), avec différents degrés de talent (intelligence, compétences, etc.) répartis de manière aléatoire sur des positions fixes dans le monde carré de 201 × 201 sections avec des conditions aux limites cycliques. Au cours de chaque simulation, qui s'étend sur plusieurs décennies, ils sont exposés à un certain nombre d'événements N _E réussis (cercles verts) et infructueux (cercles rouges) qui se déplacent dans le monde selon des trajectoires aléatoires (marche aléatoire). Dans cet exemple, N _E = 500.

Nous considérons N individus avec T _i talent (intellect, compétences, capacités, etc.) ayant une distribution normale dans l'intervalle [0; 1] autour d'une moyenne donnée m _T avec un écart-type σ _T placé aléatoirement à des positions fixes dans le monde carré (voir figure 1) avec des conditions aux limites cycliques (c'est-à-dire avec une topologie toroïdale) et entouré d'un certain nombre N _{E de} «déplacement» les événements (marqués de points), dont certains sont réussis, aucun autre (les événements neutres dans ce modèle ne sont pas pris en compte, car ils n'ont pas de conséquences significatives sur la vie de l'individu). Sur la figure 1, nous avons montré ces événements sous forme de points colorés: réussis en vert et avec un pourcentage relatif p _L , et infructueux en rouge et avec un pourcentage ( 100 - p _L ). Le nombre total de points d'événement N _E est uniformément distribué, mais, bien sûr, une telle distribution ne sera idéalement uniforme que pour N _E → ∞ . Dans nos simulations, il y aura généralement N _E ≈ N / 2 , donc, au début de chaque simulation, il y a une concentration significative aléatoire de points d'événement réussis ou non dans diverses régions du monde, tandis que d'autres régions seront plus neutres. Le mouvement aléatoire ultérieur de points à l'intérieur d'une matrice carrée, c'est-à-dire le monde, ne change pas cette caractéristique fondamentale du modèle, qui indique un nombre différent d'événements de réussite ou d'échec pour différentes personnes tout au long de leur vie, sans dépendre de leur talent personnel.

Figure 2: répartition normale des talents au sein de la population (avec la médiane m _T = 0,6 représentée par une ligne verticale en pointillés et l'écart-type σ _T = 0,1 - les valeurs m _T ± σ _{T sont} affichées sous forme de deux lignes verticales en pointillés). Cette distribution est allouée dans l'intervalle [0; 1] et ne change pas pendant la simulation.

Un cycle de simulation examine une durée de vie active P de 40 ans (âgés de vingt à soixante ans), avec un pas de temps δ _t de six mois. Au début de la simulation, tous les agents ont reçu le même capital C _i = C (0) Ɐ _i = 1, ..., N , représentant leur niveau de succès / bien-être de départ. Ce choix a pour objectif évident de ne donner à personne l'avantage initial. Bien que les talents des agents ne dépendent pas du temps, leur capital change. Au cours du développement de ce modèle, c'est-à-dire pendant la période prévue de la vie des agents, tous les points d'événement se déplacent de manière aléatoire dans le monde et, en même temps, peuvent se croiser avec l'emplacement de certains agents. Si vous entrez dans les détails, chaque point d'événement couvre, dans un sens aléatoire, la distance de 2 sections. Nous pensons qu'il existe une intersection avec l'individu si le point d'événement représenté à l'intérieur du cercle avec un rayon d'un segment est centré sur l'agent (les points d'événement ne disparaissent pas après l'intersection).En fonction d'un tel incident, à ce stade t (c'est-à-dire tous les six mois), avec un certain agent A _k , les trois options possibles suivantes sont possibles:

Aucun point d'événement ne traverse la position de l'agent A _k - cela signifie qu'au cours des six derniers mois, aucun événement de ce type ne s'est produit, l'agent A _k n'effectue aucune action.
A _k – , ( , [30], , ); , A _k / , T _k . C _k (t) = 2C _k (t − 1) , rand[0; 1] < T _k , .., , .
A _k – , ; , A _k / , .. C _k (t) = C _k (t − 1) / 2 .

Les règles ci-dessus pour les agents (y compris le choix de diviser le capital initial en deux en cas d'événements non réussis et de doubler dans le cas d'événements réussis, proportionnellement au talent de l'agent) sont intentionnellement simples et peuvent être considérées comme répandues, car elles reposent sur le fait évident que le succès dans la vie quotidienne a la propriété les deux croissent et diminuent à un rythme rapide. De plus, ces règles donnent un avantage significatif aux personnes très talentueuses, car elles peuvent bénéficier davantage des opportunités offertes par la chance (y compris la possibilité d'utiliser une bonne idée qui trouve son origine dans leur cerveau). D'un autre côté, par exemple, un accident de voiture ou une maladie soudaine, sont toujours des événements infructueux dans lesquels le talent n'a pas d'importance. À cet égard, nous pouvons tirer une définition plus précise du "talent",le définissant comme «toute qualité personnelle qui augmente les chances de saisir l'opportunité». En d'autres termes, par le terme «talent», nous entendons, au sens large, l'intelligence, les compétences, l'ingéniosité, la ténacité, la détermination, le travail acharné, la prise de risques, etc. De plus, nous verrons que l'avantage d'avoir un grand talent est une condition nécessaire mais pas suffisante pour atteindre des sommets de réussite très élevés.

2.1. Résultats d'une exécution

Dans cette sous-section, nous avons présenté les résultats d'une série de simulations typiques. De manière générale, ces résultats sont assez stables, par conséquent, comme nous le montrons ci-dessous, ils peuvent être considérés comme substantiellement représentatifs du cadre général qui sort de notre modèle.

Imaginons N = 1000 agents avec une quantité égale de capital d'amorçage C (0) = 10 (en unités abstraites) et avec un talent fixe T _i ϵ [0; 1], la distribution normale suivante avec une médiane m _T = 0,6 et un écart type σ _T = 0,1 (voir figure 2). Comme mentionné précédemment, la simulation couvre un laps de temps réaliste P= 40 ans, évoluant par étapes égales, six mois chacune, au total à partir de I = 80 itérations. Dans cette simulation, nous avons pris N _E = 500 points d'événement, avec la probabilité d'événements réussis p _L = 50%.

À la fin de la simulation, comme le montre le diagramme (a) de la figure 3, nous avons constaté que des règles de modèle dynamique simples peuvent produire une distribution inégale du capital / succès, avec un grand nombre d'agents pauvres (infructueux) et un petit nombre d'agents extrêmement riches (réussis). Après avoir construit la même distribution sur une échelle bilogarithmique, dans le schéma (b) de la même figure, nous voyons la distribution selon la fonction de puissance dans le style de Pareto, dont la pente correspond à la fonction y © ≈ C ^−1,27 .

Ainsi, malgré la répartition normale des talents, le modèle TPU semble avoir pu saisir la première caractéristique importante observée par rapport aux données réelles: l'écart le plus profond entre riches et pauvres et la nature invariable de son échelle. En particulier, dans notre simulation, seulement 4 personnes ont reçu plus de 500 unités de capital, et les 20 personnes les plus prospères possèdent 44% de toutes les valeurs, tandis que près de la moitié de la population a moins de 10 unités. En général, la règle de Pareto «80/20» est observée, puisque 80% de la population ne possède que 20% du capital total, tandis que les 20% restants des individus possèdent 80% de la richesse. Bien que cette inégalité semble sans aucun doute injuste, il serait quelque peu acceptable que la plupart des personnes qui réussissent soient parmi les plus talentueuses,gagnant ainsi plus d'accumulation de capital / succès que les autres. Mais est-ce vraiment ce qui se passe?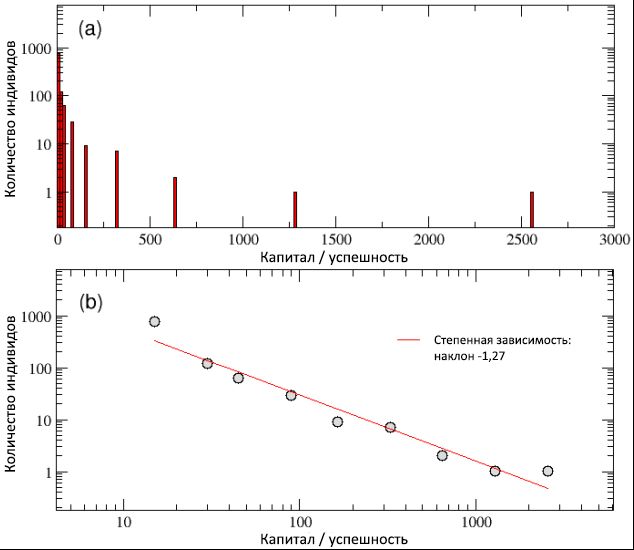

Figure 3: Répartition finale de la richesse / du succès au sein de la population, sur une échelle logarithmique linéaire (a) et bilogarithmique (b). Malgré la répartition normale des talents, la queue de la répartition des succès, comme le montre le schéma (b), peut être décrite comme une courbe de puissance avec une pente de -1,27. Nous avons également confirmé que la répartition du capital / succès suit la loi 80/20 de Pareto, puisque 20% de la population possède 80% des valeurs et vice versa.

Sur la figure 4, les schémas (a) et (b), respectivement, le talent est affiché en fonction du capital / succès total, et vice versa (notez que dans le schéma (a) le capital / succès n'a que des valeurs discrètes - cela est lié à la décision utiliser le même capital initial pour tous les agents). Un examen des deux régimes montre que, d'une part, les individus les plus performants ne sont pas les plus talentueux et, inversement, les individus les plus doués ne sont pas les plus performants. En particulier, l'individu le plus performant, avec C _max = 2560, a le talent T * = 0,61, qui n'est que légèrement supérieur à la valeur médiane m _T = 0,6, tandis que le plus doué ( T _max= 0,89) a un capital / taux de réussite inférieur à 1 unité ( C = 0,625).

Comme nous l'apprenons plus en détail dans la sous-section suivante, ce résultat n'est pas un cas particulier, mais plutôt une règle pour les systèmes de ce type: un succès maximum ne coïncide jamais avec un talent maximum, et vice versa. De plus, cet écart entre le succès et le talent est disproportionné et très non linéaire. En fait, le capital moyen de toutes les personnes talentueuses T> T * est C≈ 20; en d'autres termes, le capital / succès des personnes les plus performantes avec des talents modérés est 128 fois plus élevé que le capital / succès moyen des personnes qui sont beaucoup plus douées que les premières. Nous pouvons conclure que si le talent exceptionnel n'est pas caché derrière la raison de l'énorme succès de certaines personnes, alors, peut-être, il y a un autre facteur. Notre simulation montre clairement que la chance pure est un tel facteur.

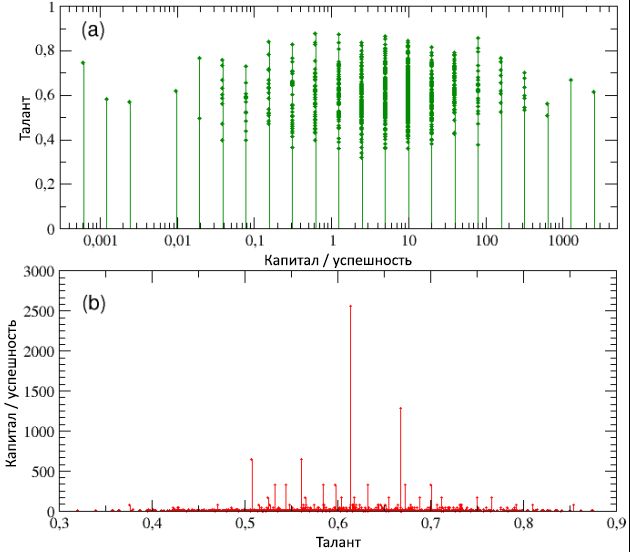Figure 4: dans le diagramme (a), le talent est affiché en fonction du capital / succès (sur une échelle logarithmique, pour une meilleure visualisation) - il indique que les individus les plus performants ne sont pas, en même temps, les plus talentueux. Dans le diagramme (b), au contraire, le capital / succès est indiqué en fonction du talent - ici, vous pouvez mieux évaluer le fait que l'agent le plus performant, avec C _max= 2560, a un talent qui ne dépasse que légèrement la valeur médiane m _T = 0,6, tandis que le plus doué a un capital / succès inférieur à C = 1 unité, beaucoup moins que le capital initial C (0). Lisez la suite pour plus de détails.

Dans la figure 5, le nombre d'événements réussis et infructueux survenus avec toutes les personnes au cours de la période de leur vie professionnelle est indiqué en fonction de leur capital / succès total. En considérant le schéma (a), il devient évident que les individus les plus performants sont en même temps les plus réussis (notez que ce diagramme montre tous les événements réussis qui sont arrivés aux agents, et pas seulement ceux dont ils ont pu bénéficier, conformément à avec votre talent). Au contraire, lorsque nous examinons le schéma (b), nous voyons que les plus infructueux en même temps sont les plus infructueux. En d'autres termes, bien qu'il n'y ait pas de corrélation entre le succès et le talent, basé sur des simulations, il y a une forte dépendance du succès à la chance. En analysant les détails des distributions de fréquence du nombre d'événements réussis et infructueux survenus avec des individus, nous avons trouvécomme le montrent les diagrammes © et (d), que ces deux valeurs sont exponentielles, avec des degrés de 0,64 et 0,48, et des médianes de 1,35 et 1,66, respectivement, et que le nombre maximal d'événements réussis et infructueux s'est produit, respectivement, 10 et 15. De plus, environ 16% ont eu une vie «neutre», généralement sans événements réussis et infructueux, tandis que 40% des individus n'ont rencontré qu'un seul type d'événement (réussi ou non).tandis que 40% des individus n'ont rencontré qu'un seul type d'événement (réussi ou non).tandis que 40% des individus n'ont rencontré qu'un seul type d'événement (réussi ou non).

Il est également intéressant de regarder la période de développement du succès / capital pour les individus les plus réussis et pour les plus infructueux, en comparant avec les séquences correspondantes d'événements réussis et infructueux qui se sont produits sur 40 ans (80 intervalles, 6 mois chacun) de leur vie professionnelle. Les résultats peuvent être vus, respectivement, dans les parties gauche et droite de la figure 6. Contrairement au schéma (a) de l'image 5, les schémas inférieurs de cette figure ne contiennent que les événements réussis dont les agents, grâce à leur talent, ont pu bénéficier.

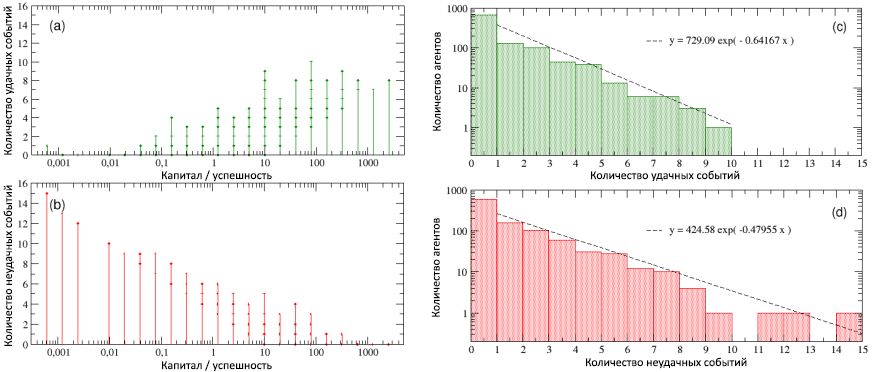Figure 5: nombre total d'événements réussis (a) et non réussis (b), en fonction du succès du capital / agent. Le graphique montre une forte corrélation entre le succès et le succès: les individus les plus performants sont également les plus performants, et vice versa. Encore une fois, en raison de l'utilisation du même capital initial pour tous les agents, il s'avère qu'un certain nombre d'événements sont regroupés en valeurs discrètes de capital / succès. Dans les diagrammes © et (d), la fréquence des distributions, respectivement, du nombre d'événements réussis et non réussis est affichée sur une échelle log-linéaire. Comme on peut le voir, les deux distributions peuvent être écrites sous forme de dépendances exponentielles avec des puissances négatives similaires).

Sur les diagrammes (supérieur et inférieur) (a) de la figure 6, concernant un individu modérément talentueux mais ayant le plus de succès, on voit clairement qu'après environ la moitié de sa vie professionnelle, accompagné d'une manifestation rare d'événements réussis (diagramme inférieur), et d'un faible niveau de capital (supérieur ), la concentration soudaine d'événements favorables survenus entre 30 et 40 pas de temps (c'est-à-dire juste avant le 40e anniversaire de l'agent) a conduit à une augmentation rapide du capital qui, au cours des 10 dernières étapes (c'est-à-dire au cours des 5 dernières années de la carrière de l'agent ) est devenu exponentiel en passant de C = 320 à C _max = 2560.

D'autre part, en regardant les diagrammes (supérieur et inférieur) (b) de la même figure concernant l'individu le moins bien réussi, il devient évident qu'une deuxième moitié particulièrement infructueuse de sa vie professionnelle, accompagnée d'une douzaine d'événements indésirables, a constamment réduit le capital / succès, conduisant à la finale valeur C = 0,00061. Il est intéressant de noter que le talent de ce malheureux agent était T= 0,74, ce qui est supérieur à la plupart des plus réussis. De toute évidence, créer la différence a été influencé par la chance. Et s'il est vrai que l'agent le plus performant méritait de bénéficier de toutes les opportunités qui lui sont offertes (malgré son talent médiocre), il est également vrai que si votre vie est pleine de malheurs et ne vous offre pas d'opportunités, comme ce deuxième agent, alors même le plus grand talent devient impuissant face à un échec violent.

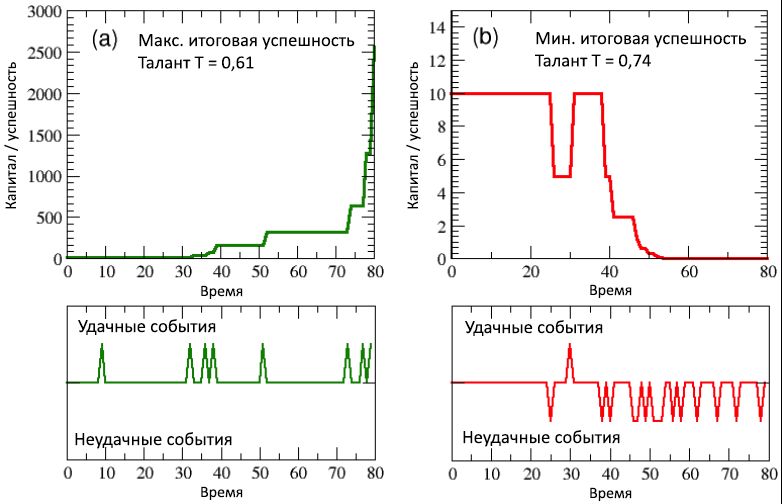Figure 6: (a) la période de développement du succès / capital de l'individu le plus performant et (b) le plus malheureux, comparé selon les séquences correspondantes d'événements réussis et infructueux survenus au cours de leur vie professionnelle (sur 80 demi-années, soit 40 ans). Le moment d'apparition de ces événements est noté dans les diagrammes inférieurs sous la forme de pics ascendants et descendants.

Tous les résultats d'une seule exécution (la version de démonstration du code NetLogo du modèle TPU utilisé pour cette simulation peut être trouvée dans le référentiel Open ABM) présentés dans cette sous-section sont très stables et, comme nous le verrons dans la sous-section suivante, ils sont enregistrés, avec de légères différences, avec de nombreuses répétitions de simulations commençant par la même répartition des talents, mais avec différentes positions aléatoires des individus.

2.2. Résultats de plusieurs exécutions

Dans cette sous-section, nous avons présenté les résultats généraux de simulation de plus de 100 analyses en moyenne, chacune ayant démarré avec des conditions initiales différentes et sélectionnées au hasard. Les valeurs des paramètres de contrôle étaient les mêmes que dans la sous-section précédente: N = 1000 individus, m _T = 0,6 et σ _T = 0,1 pour la répartition normale des talents, I = 80 itérations (chacune représente δ _t = 6 mois de vie professionnelle) ), C (0) = 10 unités de capital initial, N _E = 500 points d'événement et le pourcentage d'événements réussis p _L = 50%.

Dans le diagramme (a) de la figure 7, la distribution totale du capital total / succès parmi tous les agents collectés à la suite de 100 exécutions est représentée sur une échelle logarithmique et est bien décrite par une courbe de loi de puissance avec un coefficient angulaire -1,33. La propriété du capital constant observée en une seule série quelle que soit son échelle et la forte inégalité qui en résulte entre les individus, ainsi que la règle de Pareto «80/20», ont ainsi été préservées dans le cas de plusieurs séries. En fait, l'écart entre les agents riches (qui réussissent) et les agents pauvres (qui échouent) s'est même élargi, car le capital des personnes les plus riches dépasse maintenant les 40 000 unités.

Ce résultat peut être mieux estimé en examinant le schéma (b) de la figure 7, où le capital total C _{max des} seules personnes les plus performantes est indiqué en fonction du talent montrant le meilleur résultat dans chacune des 100 courses. L'agent avec le talent T _best = 0,6048, coïncidant presque avec la médiane de la distribution des talents ( m _T = 0,6), qui a atteint le pic de capital C _best = 40960, a reçu le plus de points. En revanche, le plus doué des individus les plus performants, avec talent T _max = 0,91, capital gagné C _max = 2560, soit seulement 6% de C _meilleur .

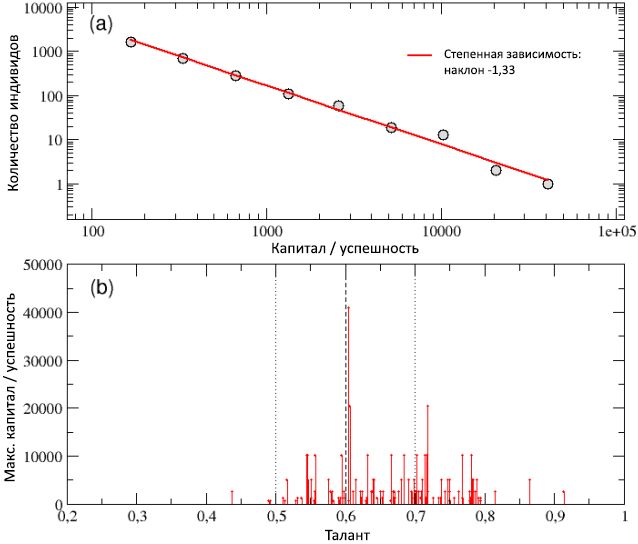
Figure 7: Schéma (a) - distribution du capital total / succès calculé sur 100 séries pour des populations avec différentes conditions initiales déterminées au hasard. La distribution peut être décrite par une courbe de puissance avec une pente de -1,33. Schéma (b) - le capital total C _{max des} individus _les plus performants dans chacune des 100 courses, indiqué en fonction de leur talent. Les personnes ayant un talent modérément élevé, en moyenne, ont plus de succès que celles qui ont un talent faible ou modéré, et le plus souvent, la personne la plus performante est un agent modérément doué, et seulement occasionnellement le plus talentueux. La valeur de m _T , ainsi que les valeurs de m _T ± σ _T , sont représentées respectivement sous la forme de lignes verticales en pointillés et en pointillés.

Afin d'examiner ce point de vue plus en détail, dans la figure 8 (a), nous avons tracé la répartition des talents des meilleurs interprètes, calculée pour 100 runs. La distribution est évidemment décalée vers la droite le long de l'axe des talents, avec une valeur moyenne de T _av = 0,66> m _T - cela confirme, d'une part, que pour obtenir un succès significatif, un talent modérément élevé est souvent nécessaire; cependant, d'un autre côté, cela montre également que cette condition n'est presque jamais suffisante, car les agents ayant le plus grand talent (c'est-à-dire avec T > m _T = 2σ _T , ou T > 0,8) sont parmi les meilleurs dans 3% des cas, et leur capital / succès ne dépasse jamais 13% de C _meilleur .

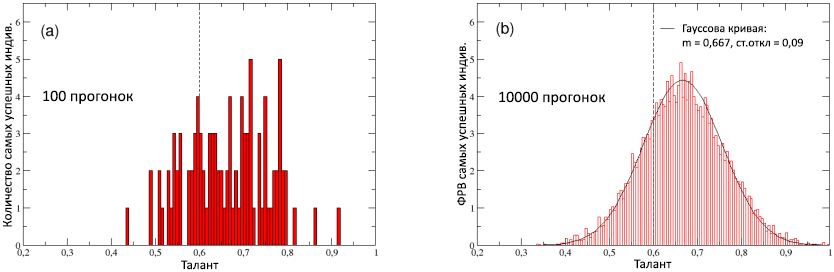
Figure 8: (a) Répartition des talents des personnalités les plus performantes (les plus performantes) dans chacune des 100 courses. (b) La fonction de distribution de probabilité (RFF) du talent des individus les plus performants, calculée en 10 000 runs: est bien décrite par la distribution normale avec une médiane de 0,667 et un écart-type de 0,09 (courbe continue). À titre de comparaison, la médiane m _T = 0,6 de la distribution normale initiale des talents dans la population est indiquée, représentée dans les deux schémas par une ligne verticale en pointillés.

Dans le diagramme (b) de la figure 8, la même distribution (réduite à la surface totale pour obtenir le FRF) est calculée pour 10000 essais afin de comprendre sa vraie forme: il semble qu'elle s'insère dans la courbe gaussienne G (T) avec la moyenne T _av = 0,667 et un écart type de 0,09 (ligne continue). Cela confirme bien sûr que la répartition des talents des meilleurs interprètes est décalée vers la droite par rapport à l'axe des talents, par rapport à la répartition initiale. Pour être plus précis, cela signifie que la probabilité conditionnelle P ( C _max | T ) = G (T) dT de trouver parmi les meilleurs interprètes une personnalité de talent dans l'intervalle [ T ; T + dT ] croît avec le talent T , culmine près du talent moyennement moyen à moyen T _av = 0,66, puis diminue fortement avec de grandes valeurs de talent. En d'autres termes, la probabilité de trouver un individu modérément talentueux en plus du succès est plus élevée que d'y trouver un individu très doué. Notez que dans un monde idéal où le talent est la principale raison du succès, on s'attend à ce que P ( C _max | T ) soit une fonction croissante de T. Ainsi, nous pouvons conclure que la forme gaussienne observée P ( C _max | T ) témoigne d'une plus grande importance de la chance que du talent pour atteindre des niveaux de réussite extrêmement élevés.

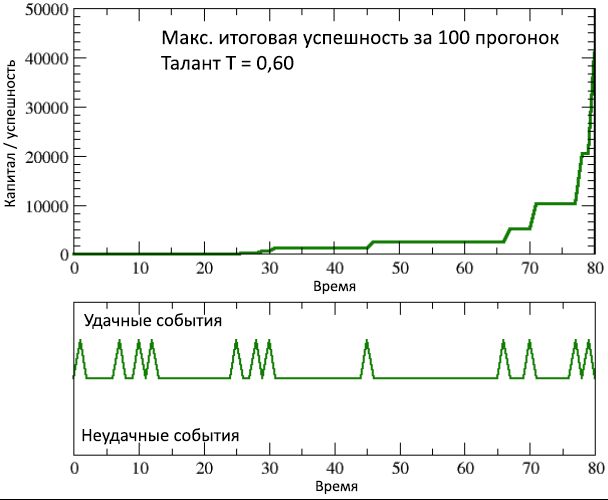
Figure 9: changement dans le temps de réussite / capital de la personne la plus réussie (mais en même temps, modérément douée), sur 100 cycles de simulation, par rapport à la séquence inhabituelle correspondante d'événements réussis qui se sont produits dans sa vie.

Il est également intéressant de comparer, à partir de 100 runs, le taux moyen de capital / succès C _mt ≈ 63 des personnes les plus talentueuses avec la moyenne C correspondante _à ≈ 33 de celles dont le talent est proche de la médiane m _T. Dans les deux cas, nous avons trouvé des indicateurs plutôt faibles (même si plus que le capital initial C (0) = 10), mais le fait que C _mt > C _at indique que bien que la probabilité de trouver un individu moyennement talentueux au sommet du succès soit plus élevée, que celui qui est très doué, les individus les plus talentueux de chaque course ont, en moyenne, plus de succès que les personnes modérément douées. En revanche, si l'on considère la moyenne sur 100 runs, la proportion d'individus avec talent T > 0,7 (c'est-à-dire plus élevée qu'avec un écart-type de la médiane) et le succès final / capital C _fin > 10, calculé en tenant compte de tous les agents avec talent T > 0,7 (dont, en moyenne pour chaque course, ≈ 160), nous avons constaté que cette part est de 32% - cela signifie que la performance combinée des personnes les plus talentueuses de notre population est, en moyenne, relativement faible, car seule un tiers d'entre eux atteignent un capital total supérieur à l'original.

En tout cas, le fait que le meilleur performant parmi les 100 simulations soit un agent avec le talent T _best = 0,6, qui correspond parfaitement à la médiane, et avec le succès final C _best = 40960, soit 650 fois plus que C _mt , est _irréfutable . et plus de 4 000 fois supérieur au succès de C _end <10 sur 2/3 des personnes les plus talentueuses. Cela s'est finalement produit, simplement parce qu'il a eu plus de chance que les autres. Chance inconditionnelle, comme le montre la figure 9, qui montre la croissance de son capital / succès tout au long de sa vie professionnelle, ainsi qu'une impressionnante série d'événements réussis (et seulement réussis), dont, malgré le manque de talent exceptionnel, il a pu profiter au cours de sa carrières.

En résumé, à ce stade, il a été constaté que, malgré sa simplicité, le modèle TPU semble être en mesure de prendre en compte de nombreuses caractéristiques qui caractérisent, comme cela a été mentionné dans l'introduction, la forte inégalité dans la répartition des richesses et du succès dans notre société, qui contraste clairement avec la répartition gaussienne des talents parmi les les gens. En outre, le modèle sous forme quantitative montre qu'un grand talent ne suffit pas pour garantir une carrière réussie et qu'au contraire, les personnes les moins douées atteignent très souvent le summum du succès - c'est un autre `` fait conditionnel '' souvent observé dans la vie réelle [35, 36, 38].

Un aspect clé qui explique intuitivement comment il peut arriver que des individus modérément doués obtiennent (si souvent) beaucoup plus d'honneur et de succès, par rapport à d'autres plus talentueux, est qu'il y a un rôle caché et souvent sous-estimé de la chance, comme il est clairement vu de nos simulations. Mais pour comprendre le vrai sens des résultats de nos recherches, il est important de distinguer entre macro et micro point de vue.

En fait, au niveau micro, suivant les règles dynamiques du modèle TPU, un individu doué est a priori plus susceptible d'atteindre un niveau de réussite élevé qu'un modérément talentueux, car il a une plus grande capacité à saisir l'opportunité. Ainsi, du point de vue d'un individu, nous devrions conclure que, étant incapable (par définition) d'influencer l'apparition d'événements réussis, la meilleure stratégie pour augmenter les chances de succès (à tout niveau de talent) est d'élargir l'activité personnelle, de générer des idées, de communiquer avec les autres, la recherche de la diversité et de l'enrichissement mutuel. En d'autres termes, devenir une personne à l'esprit large, prête à contacter les autres donne la plus grande probabilité de réussite d'un événement (qui se réalisera dans la mesure du talent de l'individu).

D'un autre côté, au niveau macro, du point de vue de l'ensemble de la société, la probabilité de rencontrer des individus modérément doués au sommet du succès est beaucoup plus élevée que d'y trouver des personnes extrêmement talentueuses, car les premiers sont beaucoup plus grands et, grâce à la chance, ils ont, en général, des statistiques l'avantage de remporter un immense succès, malgré leurs propres chances personnelles a priori plus faibles.

Dans la section suivante, nous examinerons ce point de vue au niveau macro, en explorant les opportunités offertes par notre modèle afin d'étudier plus en détail des stratégies et des politiques plus efficaces pour améliorer le niveau moyen de performance des personnes les plus talentueuses de la population, en mettant en œuvre des moyens plus productifs de distribution des récompenses et des ressources. En fait, nous nous attendons à ce que toute politique qui puisse augmenter le niveau des individus les plus talentueux qui sont le moteur du progrès et de l'innovation dans notre société aura un effet bénéfique cumulatif.

3. Stratégies efficaces d'équilibrage de chance

Les résultats présentés dans la section précédente sont clairement cohérents avec les preuves empiriques documentées dans l'introduction, qui remettent en question l'hypothèse méritocratique selon laquelle les différences naturelles de talent, de compétences, d'aptitudes, d'intelligence, de dur labeur ou de persévérance sont les seules raisons du succès. Comme nous l'avons montré, la chance a également un impact et peut jouer un rôle crucial. L'essence de la discussion est qu'en raison de la difficile mesurabilité (dans de nombreux cas, il est difficile de déterminer en termes exacts) des qualités personnelles, les stratégies méritocratiques sont souvent utilisées pour distribuer des récompenses, des financements ou des récompenses, souvent basées sur des résultats privés, mesurés en termes de richesse ou de succès personnel. En conséquence, ces stratégies influencent l'action future pour renforcer et pomper la richesse / le succès des individus les plus performants en raison du mécanisme de rétroaction positive, qui est similaire au processus «riche devient riche» (également connu sous le nom d '«effet Matthew» [57, 58, 59]) , avec un résultat injuste.

Imaginons, par exemple, un conseil de recherche et développement financé par le gouvernement et doté d'un montant fixe. Qu'est-ce qui sera beaucoup plus efficace pour augmenter l'efficacité moyenne de la recherche: accorder des subventions importantes à quelques scientifiques sans doute excellents ou de petites subventions à de nombreux scientifiques manifestement plus ordinaires? Une étude récente [44], basée sur une analyse de quatre indices de l'importance scientifique des publications connexes, a révélé que l'importance n'a qu'une faible relation positive avec le financement. En particulier, l'importance du dollar était plus faible pour les grands détenteurs de subventions, et l'importance des scientifiques qui ont reçu des augmentations de financement n'a pas augmenté de façon appropriée. Les auteurs de l'étude ont conclu que l'importance scientifique (telle que reflétée dans la publication) ne limite que faiblement le financement, et ont suggéré que les stratégies de financement visant à diversifier les idées plutôt que «l'excellence» sont susceptibles d'être plus productives. Une contribution ultérieure [60] a montré que, tant par le nombre de documents produits que par leur importance scientifique, la concentration du financement de la recherche entraîne généralement une baisse des rendements marginaux, et aussi que les chercheurs les plus financés ne se distinguent pas en termes d'efficacité et de signification scientifique. En général, de telles conclusions ne devraient pas être surprenantes à la lumière d'une autre découverte récente [18], qui déclare que la signification, telle que mesurée par des publications influentes, est répartie au hasard dans un certain nombre de publications du scientifique. En d'autres termes, la chance compte, et si elle affecte plus que nous ne voulons l'admettre, il n'est pas surprenant que les stratégies méritocratiques soient moins efficaces que prévu, surtout si nous essayons d'apprécier le mérite a posteriori. Dans les études précédentes [48, 49, 50, 51, 52, 53, 54, 55], il y avait déjà un avertissement contre ce type de «quasi-méritocratie», montrant l'efficacité des stratégies alternatives basées sur des élections aléatoires dans les domaines de la gestion, de la politique et des finances. Selon ce point de vue, le modèle TPU montre comment le niveau minimum de réussite peut être augmenté pour la plupart des personnes talentueuses dans le monde où la chance compte, et la découverte accidentelle conduit souvent à des réalisations importantes.

3.1. Découvertes accidentelles, innovation et stratégies de financement efficaces

Le terme «découverte accidentelle» est largement utilisé dans les références littéraires à des faits historiques, montrant que les chercheurs font souvent des découvertes inattendues et utiles par pur hasard, lorsqu'ils cherchent autre chose [61, 62]. Il existe une longue liste d'histoires de découvertes faites exclusivement par coïncidence: de la pénicilline par Alexander Fleming à la radioactivité par Marie Curie, du rayonnement de fond micro-ondes cosmique par les radio-astronomes Arno Penzias et Robert Woodrow Wilson au graphène Andrei Geim et Konstantin Novosyolov. Voici un exemple plus récent: un réseau de canaux remplis de liquide dans le corps humain, un organe jusque-là inconnu qui favorise apparemment la propagation des cellules cancéreuses, a été découvert par hasard, lors d'une endoscopie simple [63]. Par conséquent, beaucoup de gens pensent que la recherche motivée par la curiosité devrait toujours être financée, car personne ne peut vraiment savoir à l'avance ou prédire à quoi elles mènent [64].

Est-il possible de quantifier l'importance d'une découverte aléatoire? Quels sont les moyens les plus efficaces pour simuler une découverte aléatoire? Elle peut prendre de nombreuses formes différentes, et il est difficile de la limiter et de la quantifier. C'est pourquoi, jusqu'à présent, les études universitaires ont considéré une découverte scientifique accidentelle, pour la plupart, comme un concept philosophique. Mais les temps changent. Le Conseil européen de la recherche a récemment accordé une subvention de 1,7 million de dollars au biochimiste Ohid Yakubu pour calculer l'importance d'une découverte accidentelle en science [65]. Yakub a découvert que la découverte aléatoire peut être classée en quatre types de base [66] et qu'il peut y avoir des facteurs importants qui influencent son apparence. Ses résultats semblent coïncider avec des idées développées dans des recherches antérieures [67, 68, 69, 70, 71, 72], qui soutiennent que les stratégies généralement acceptées, clairement méritocratiques, qui visent la supériorité et supplantent la diversité semblent destinées à perdre et inefficace. La raison en est qu'ils rejettent a priori des recherches qui paraissaient initialement moins prometteuses, mais qui, grâce notamment à une découverte aléatoire, pourraient a posteriori être incroyablement innovantes.

De ce point de vue, nous souhaitons appliquer le modèle TPU, qui exprime naturellement la chance (et, par conséquent, la découverte aléatoire) comme paramètre quantitatif de la stratégie, afin d'étudier l'efficacité de différents scénarios de financement dans cette sous-section. En particulier, dans les situations où, comme mentionné ci-dessus, une personne modérément talentueuse mais chanceuse a souvent plus de succès que des individus plus doués mais malchanceux, il est important d'évaluer l'efficacité des stratégies de financement pour la capacité de maintenir un niveau minimum de succès, y compris pour les personnes les plus talentueuses qui sont censées apporter les idées les plus innovantes et progressistes.

En commençant par les mêmes paramètres initiaux que ceux utilisés dans la sous-section 2.2, c'est-à-dire N = 1000, m _T = 0,6, σ _T = 0,1, I = 80, δ _t = 6, C (0) = 10, NE = 500, p _L = 50% et 100 cycles de simulation, imaginons que le capital de financement total disponible F _{T soit} périodiquement réparti entre les individus selon différents critères. Par exemple, les finances peuvent être émises:

Partage également (critères égalitaires) pour encourager la diversité de la recherche;
Seul un certain pourcentage des individus les plus performants («meilleurs») (critère élitiste), qui était auparavant appelé la «quasi» méritocratie, pour la répartition des finances entre les personnes en fonction des performances passées.
Répartition "premium" entre une certaine proportion des individus les plus performants et le reste, en petites parts égales, par rapport au reste (critère mixte);
Seul un certain pourcentage d'individus sélectionnés au hasard (critère aléatoire aléatoire).

Nous supposons de façon réaliste que le capital total F _T sera alloué tous les 5 ans, au cours de la période de 40 ans de chaque simulation, de sorte que F _T = 8 unités de capital sera distribué de temps à autre . Par des injections périodiques de ces finances, nous entendons maintenir un niveau minimum de ressources des agents les plus talentueux. Ainsi, un bon indicateur de l'efficacité de la stratégie de financement choisie peut être le pourcentage P _T , en moyenne pour 100 simulations, pour les individus talentueux T > m _T + σ _T , dont le succès / capital total dépasse le niveau initial, c'est-à-dire C _end> C (0).

Ce pourcentage a déjà été calculé lors des simulations présentées dans la sous-section 2.2. Cela montre qu'en l'absence de financement, la meilleure performance a été obtenue par les agents les plus performants avec des talents proches de la moyenne, tandis que le capital / succès des personnes les plus talentueuses reste toujours extrêmement faible. En particulier, seule une partie de P _T0 ≈ 32% du nombre total d'agents de talent T > 0,7 a pu atteindre, sur la base des résultats de la simulation, un capital / succès supérieur à la valeur initiale. Par conséquent, pour comparer l'efficacité des différentes stratégies de financement, la croissance du pourcentage moyen P _{T par} rapport à P _T0 doit être calculéeces personnes talentueuses qui ont augmenté leur capital initial au cours de leur carrière. Définissons cette croissance comme P ^* _T = P _T - P _T0 . Cette valeur est un indicateur assez stable: nous l'avons vérifié en répétant à partir de 100 simulations, l'écart des valeurs P ^* _T est resté inférieur à 2%. Enfin, si nous calculons le ratio P ^* _T sur le capital total réparti sur tous les agents sur 40 ans, nous pouvons obtenir un indice d'efficacité E , qui mesure la croissance du nombre de personnes talentueuses suffisamment réussies par unité de capital investi, défini comme E = P ^* _T/ Le F _T .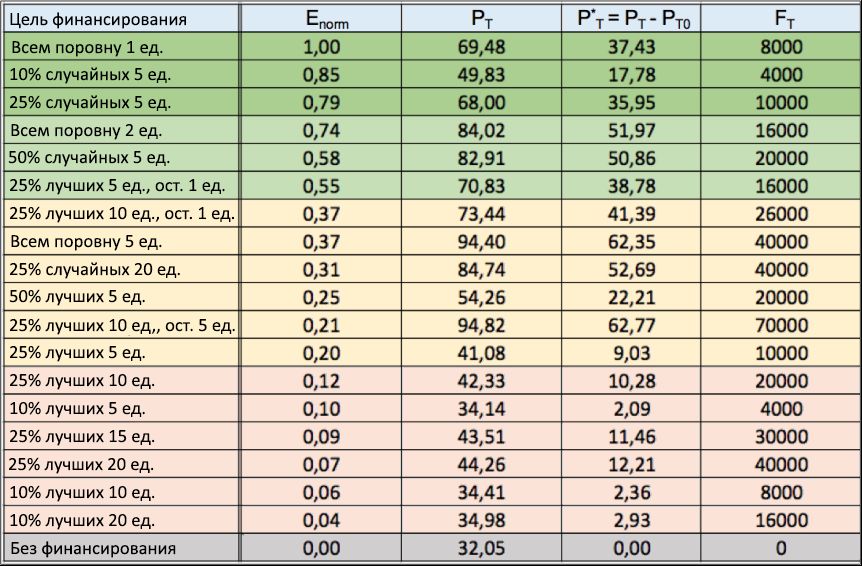

Figure 10: Tableau des stratégies de financement. Plusieurs stratégies de répartition des financements à des fins diverses (1 colonne) sont présentées, avec les résultats de la _{norme d'} indice d'efficacité normalisé E (2 colonnes), par ordre décroissant. Aussi, dans les troisième et quatrième colonnes, respectivement, les valeurs de la part P _{T des} personnes talentueuses ayant réussi et l'augmentation nette de leur nombre P ^* _T sont indiquées , par rapport au scénario «sans financement», en moyenne pour 100 simulations. Enfin, la dernière colonne montre le capital total F _T investi dans chaque cycle.

, 10, (2- ), , (1 ), P _T (3- ) P ^* _T (4- ). , , F _T . E E _max , () E _norm = E / E _max. Pour le scénario avec un manque de financement, par définition, _norme E = 0. Les mêmes résultats de la _norme E sont présentés en fonction des stratégies de financement adoptées sous la forme d'un histogramme sur la figure 11. En raison de la stabilité statistique P _T montrant des écarts de moins de 2%, les résultats donnés de l'indice d'efficacité E _{la norme} sont stables.

11, , ( ), ( ) , , , .

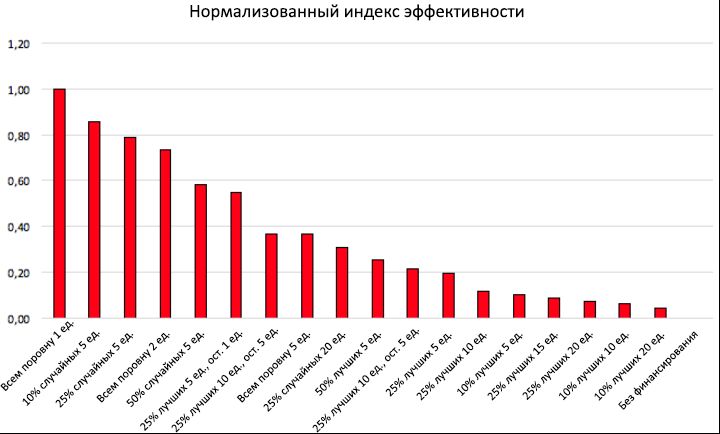
11: . E _norm . , , C _end> C (0), il est beaucoup plus efficace de répartir de petites sommes de financement entre de nombreuses personnes que de financer par d'autres moyens plus sélectifs.

D'une part, l'histogramme montre que le critère «égalitaire», qui alloue 1 unité de capital à chaque individu tous les 5 ans, est le moyen le plus efficace de répartir les finances, avec la _norme E = 1 (c'est-à-dire E = E _max ): pour relativement petits investissements F _T à hauteur de 8000 unités, il s'avère doubler le pourcentage de personnes talentueuses performantes, par rapport au scénario «sans financement», le faisant passer de P _T0 = 32,05% à P _T = 69,48%, P ^* _T = 37,43. (, 2 5 ), ( 69,48% 94,40%), , E _norm = 1 E _norm = 0,74, E _norm = 0,37, .

, «» , 5 (5, 10, 15 20 ) 50%, 25% 10% , , _Norme E <0,25 dans tous ces scénarios, la croissance nette P ^* _{T du} nombre total de talents talentueux, par rapport au scénario «sans financement», reste extrêmement faible (dans presque tous les cas moins de 20%), souvent malgré un investissement beaucoup plus important par rapport à une stratégie égalitaire similaire. Ces résultats renforcent l'hypothèse selon laquelle une telle approche n'est évidemment pas bien méritocratique.

, «» , .. «» , , 25%, , , « » , . , «» . , , : 16000 , P _T , , , (70,83% 84,02%), E _norme (0,55 vs 0,74).

Si nous prenons en compte des facteurs psychologiques (non modélisés dans cette étude), alors la stratégie mixte peut être reconsidérée par rapport à celle égalitaire. En fait, la récompense bonus attribuée aux individus les plus performants peut stimuler une plus grande adhésion de tous les agents, tandis que le reste également réparti jouera un double rôle: au niveau individuel, il stimulera la diversité et offrira de nouvelles opportunités aux personnes talentueuses qui ne réussissent pas à réaliser leur potentiel, et le niveau général soutiendra les découvertes aléatoires, contribuant ainsi au développement de la recherche et de la communauté dans son ensemble.

, , . , , , 5 10% , 4000 , P ^* _T = 17,78%, . , 25% ( 10000 ) P ^* _T= 35,95, comparable à celle obtenue par la meilleure stratégie d'égalisation, qui a remporté la première place au classement général. Il est frappant que ce dernier résultat P ^* _T soit environ quatre fois la valeur ( P ^* _T= 9,03%) obtenu selon l'approche élitiste (voir ligne 12 du tableau), qui répartissait exactement le même capital (10 000 unités) entre le même nombre d'individus (25% du total). Ce dernier confirme encore plus que dans des environnements sociaux et économiques complexes où le hasard joue un rôle important, l'efficacité d'autres stratégies basées sur des élections aléatoires peut facilement contourner les stratégies standard basées sur l'approche «quasi méritocratique». Ce phénomène, contraire au bon sens, a déjà été observé dans les domaines de la gestion, de la politique et des finances [48, 49, 50, 51, 52, 53, 54, 55], et trouve ainsi une autre confirmation dans le cadre de l'étude du financement.

Afin de confirmer davantage les données obtenues, la figure 12 montre les résultats d'une autre série de simulations. Contrairement aux simulations précédentes, le montant total du capital investi dans chacune des 100 séries est désormais fixé à F _T = 80 000, de sorte que F _T / 8 = 10 000 unités sont réparties entre les agents tous les 5 ans , selon les mêmes stratégies de financement discutées précédemment. . En regardant le tableau, on constate que les résultats de la stratégie de péréquation ont encore été les plus efficaces en termes de récompense des personnes les plus talentueuses, avec une part de P _Tprès de 100%. Elle est suivie d'une stratégie aléatoire (avec 50% d'individus sélectionnés au hasard pour le financement), puis mixte, dans laquelle la moitié du capital est répartie entre 25% des individus les plus performants, et l'autre partie, à parts égales, entre d'autres personnes. Au contraire, toutes les stratégies d'élite se situaient à nouveau en fin de notation, confirmant ainsi encore l'inefficacité de l'approche «pas très méritocratique» pour récompenser les vrais talents.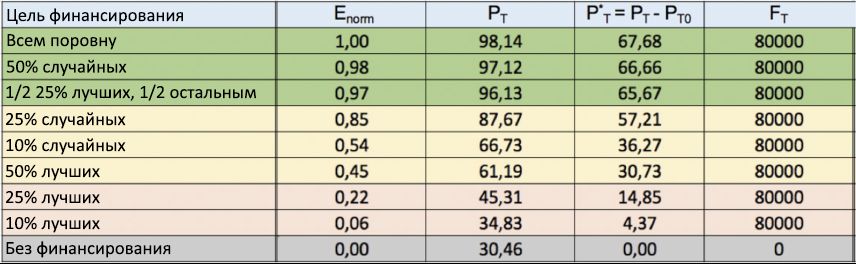

Figure 12: Tableau des stratégies de financement à financement fixe. Les indices d'efficacité normalisés obtenus E _norme pour plusieurs stratégies de distribution de financement (1ère colonne) sont à nouveau présentés par ordre décroissant, de haut en bas. Contrairement à la figure 10, ici, le capital total investi dans chaque cycle est fixé àF _T = 80 000. La stratégie de péréquation a de nouveau pris la première place.

Les résultats des simulations du modèle TPU présentés dans cette sous-section ont attiré l'attention sur l'importance des facteurs externes (comme, en effet, des politiques de financement efficaces) pour augmenter les chances de succès de la plupart des individus talentueux qui se retrouvent trop souvent punis par la coïncidence d'événements infructueux. Dans la sous-section suivante, nous examinons dans quelle mesure de nouvelles opportunités devraient provenir des changements environnementaux, tels que le niveau d'éducation ou d'autres incitations dérivées de l'environnement social dans lequel les gens vivent ou d'où ils viennent.

3.2. Importance de l'environnement

Pour commencer, évaluons le rôle du niveau moyen d'éducation dans la population. Dans le cadre du modèle TPU, il peut être obtenu en modifiant les paramètres de la répartition normale des talents. En général, si nous supposons que le talent et les compétences des individus, lorsqu'ils sont stimulés, peuvent être plus efficaces pour réaliser de nouvelles opportunités, alors l'augmentation de la médiane m _T ou de l'écart-type du talent σ _T peut être interprétée comme une conséquence de politiques visant, respectivement, soit à rehausser le niveau moyen d'éducation ou renforcer la formation des personnes les plus douées.

Dans les deux diagrammes de la figure 13, nous avons présenté le capital / succès total accumulé par les meilleurs performants de chacune des 100 courses sous la forme d'une fonction de leur talent. Les paramètres donnés correspondent à ceux utilisés dans la sous-section 2.2 ( N = 1000, I = 80, δ _t = 6, C (0) = 10, N _E = 500 et p _L = 50%), mais avec différents moments de répartition des talents . En particulier, dans le diagramme (a), nous avons laissé inchangé m _T = 0,6, mais augmenté σ _T = 0,2, tandis que dans le diagramme (b) nous avons fait le contraire, laissant σ _T = 0,1 et augmentant m_T = 0,7. Dans les deux cas, vous pouvez remarquer un décalage vers la droite des pics de réussite maximale, mais avec une différence de détails.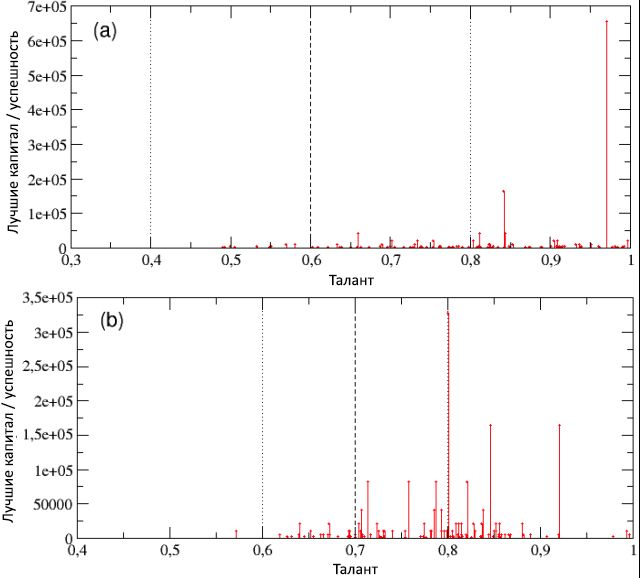

Figure 13: le capital total des individus les plus performants dans chacune des 100 pistes, présenté en fonction de leur talent pour des populations avec différents paramètres de répartition des talents: (a) m _T = 0,6 et σ _T = 0,2 (ce qui reflète le renforcement du milieu académique former les personnes les plus douées); (b) m _T = 0,7 et σ _T = 0,1 (ce qui représente une augmentation du niveau moyen d'éducation). Les valeurs correspondantes de m _T et m _T ± σ _T sont également indiquées. , , .

, , σ _T , m _T , (a), – , T = 0,97, / C _best = 655360. , , , , , , , . (b) , m _Tsans changer σ _T donne le meilleur interprète avec C _best = 327680 et talent T = 0,8, suivi de deux autres, avec C = 163840 et, par conséquent, T = 0,85 et T = 0,92. Cela suggère que dans ce cas, les chances des personnes les plus talentueuses d'atteindre un succès extrêmement élevé ont augmenté, mais en même temps, l'écart entre les malchanceux et les chanceux était plus faible qu'auparavant.

Enfin, dans les deux exemples considérés, la valeur moyenne du capital / succès des 100 personnes les plus talentueuses a augmenté par rapport à la valeur de C _mt ≈ 63 obtenue à la sous-section 2.2. En particulier, nous avons obtenu C_mt ≈ 319 dans le schéma (a) et C _mt ≈ 122 dans le schéma (b), mais ces résultats sont très spécifiques pour une série particulière de simulations. Un paramètre plus fiable pour l'expression numérique de l'efficacité des politiques sociales étudiées ici est qu'il s'agit là encore de l'indicateur P _T présenté dans la sous-section précédente, c'est-à-dire proportion moyenne de personnes talentueuses T > m _T + σ _T et réussite totale / capital C _fin > 10, par rapport au nombre total de personnes talentueuses T > m _T + σ _T (notez qu'ici, dans les deux cas,m _T + σ _T = 0,8). Nous avons donc obtenu P _T = 38% dans le schéma (a) et P _T = 37,5% pour le schéma (b), avec une légère augmentation nette par rapport à la valeur de référence P _T0 = 32% (obtenue pour la répartition des talents à m _T = 0,6 et σ _T = 0,1).

Pour résumer, nos résultats montrent que le renforcement de la formation des personnes les plus douées ou l'élévation du niveau moyen d'éducation conduit, comme on pouvait s'y attendre, à certains effets positifs dans le système social, car ces deux politiques conduisent à une augmentation de la probabilité pour les personnes talentueuses de saisir les opportunités, leur a donné de la chance. En revanche, l'amélioration de la part moyenne de personnes très talentueuses qui ont réussi à atteindre un bon niveau de réussite ne semble pas particulièrement significative pour les deux scénarios analysés. Ainsi, le résultat des politiques éducatives pertinentes semble être largement limité à la survenue de cas isolés de réussite exceptionnelle.

Bien sûr, une fois ce niveau d'éducation établi, il est devenu évident que l'abondance des opportunités offertes par cet environnement social, c'est-à-dire le pays où une personne est née accidentellement ou a décidé de vivre est un autre élément clé qui peut influencer les performances globales du système.

Dans la figure 14, nous avons présenté des résultats similaires à ceux qui étaient visibles dans l'image précédente, mais pour une autre série de simulations, avec 100 analyses chacune, avec les mêmes paramètres définis que dans la sous-section 2.2 ( N = 1000, m _T = 0, 6, σ _T = 0,1, I = 80, C (0) = 10, N _E = 500) mais avec des pourcentages différents p _Lévénements réussis (rappelez-vous que dans la sous-section 2.2, le pourcentage p _L = 50% a été pris ). Dans le schéma (a), nous prenons p _L = 80% pour simuler un environnement très stimulant et plein d'opportunités, typique des pays riches industrialisés comme les USA [26]. En revanche, dans le schéma (b), une valeur de p _L = 20% reproduit un scénario d'un environnement beaucoup moins encourageant, avec un nombre extrêmement réduit de possibilités, comme par exemple dans les pays du tiers monde.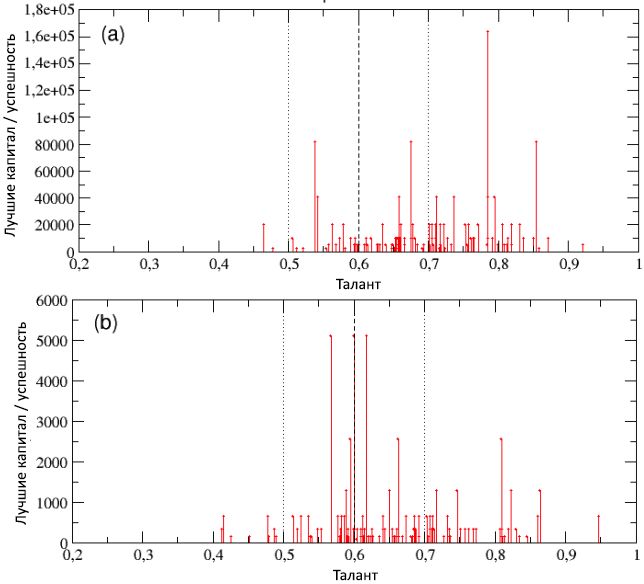

Figure 14: le capital total des individus les plus performants dans chacune des 100 pistes est indiqué en fonction de leur talent pour des populations vivant dans des environnements avec des pourcentages différents p _{L d'} événements réussis: (a) p_L = 80%; (b) p _L = 20%. , , m _T = 0,6 m _T ± σ _T , σ _T = 0,1.

, / , , p _L .

p _L = 80%, (a), - , p _L = 50%, , C _best = 163840. En revanche, la valeur moyenne du capital / succès des individus les plus talentueux, C _mt ≈ 149, est assez élevée et, surtout, il en va de même pour l'indicateur P _T = 62,18% (ce qui représente environ le double valeur de référence P _T0 = 32%), cela signifie que, comme prévu, les personnes les plus talentueuses bénéficient d'un plus grand pourcentage d'événements réussis.

Des résultats complètement différents ont été obtenus avec p _L = 20%. Bien sûr, comme le montre le schéma (b), le niveau global de réussite est maintenant très faible par rapport à ce qui a été trouvé dans les simulations de la sous-section 2.2, avec une valeur de crête de C _bests'élevant à seulement 5120 unités - c'est une trace de réduction des inégalités sociales, qui est la conséquence attendue de l'égalisation des chances de réussite. Conformément à ces résultats, l'indicateur P _T atteint également une valeur minimale, avec un pourcentage moyen de personnes talentueuses ayant réussi à augmenter leur niveau de réussite initial, égal à seulement 8,75%.

En conséquence, dans cette section, il a été démontré que l'environnement encourageant et l'abondance des opportunités associées à la stratégie appropriée pour la distribution des finances et des ressources sont des facteurs importants pour réaliser le potentiel des personnes les plus talentueuses, leur donnant plus de chances de réussir que les personnes modérément douées, mais plus chanceux. D'un point de vue macroéconomique, toute politique susceptible d'influencer ces indicateurs et de soutenir des individus talentueux se traduira par des progrès collectifs et l'innovation.

4. Remarques finales

Dans cet article, à partir d'un certain nombre d'hypothèses extrêmement simples et rationnelles, nous avons présenté un modèle d'agent capable de mesurer quantitativement le rôle du talent et de la chance dans la réussite des carrières des personnes. Les simulations ont montré que bien que le talent ait une répartition gaussienne entre les agents, la répartition finale du succès / capital, après 40 ans de vie active, suit une fonction de pouvoir selon le principe de la loi de Pareto «80/20», qui correspond à la nature de la répartition des richesses observée dans le monde réel. Un résultat important des simulations est que les agents les plus performants ne sont presque pas toujours les plus talentueux, mais ceux qui sont proches de la valeur moyenne de la distribution gaussienne des talents - un fait largement connu souvent trouvé dans la littérature.Le modèle montre l'importance souvent sous-estimée des événements réussis pour déterminer le niveau final de réussite individuelle. Étant donné que les récompenses et les ressources sont généralement distribuées à ceux qui ont déjà atteint un haut niveau de succès, utilisé à tort comme mesure de la compétence / du talent, cela conduit à une incitation négative, ce qui entraîne un manque d'opportunités pour les talents les plus élevés. Nos résultats soulignent les risques d'un paradigme que nous appelons une «quasi-méritocratie», qui n'est pas en mesure de respecter et de récompenser les personnes les plus compétentes, car il sous-estime le rôle du hasard parmi les principaux facteurs de réussite déterminants. À cet égard, plusieurs scénarios différents ont été étudiés afin d'identifier les stratégies les plus efficaces qui pourraient équilibrer le rôle imprévisible de la chance et donner plus d'opportunités et de ressources aux plus talentueux - l'intention,ce qui devrait être l'objectif principal d'une approche véritablement méritocratique. Il a également été démontré que ces stratégies sont les plus bénéfiques pour la communauté dans son ensemble, car elles conduisent à la croissance de diverses idées et perspectives dans la recherche, stimulant ainsi également l'innovation.

Remerciements

Nous tenons à remercier Robert Frank, Pavel Sobkowitz et Konstantino Tsallis pour leurs discussions et commentaires fructueux.

Bibliographie

Bak, P., Tang, C. et Wiesenfeld, K., Criticité auto-organisée. Phys. Rev. A , 38: 364 {374 (1988).
Barab´asi, A.-L., Albert, R., Emergence of Scaling in Random Networks, Science , Vol. 286, numéro 5439, pp. 509 {512 (1999).
Newman, MEJ, Power lois, distributions de Pareto et loi de Zipf, Contemporary Physics , 46 (5): 323 {351 (2005).
Tsallis, C., Introduction à la mécanique statistique non extensive. Approaching a Complex World , Springer (2009).
Pareto, V., Cours d'Economie Politique , vol. 2 (1897).
Steindl, J., Random Processes and the Growth of Firms — A Study of the Pareto Law, Charles Griffin and Company , London (1965).
Atkinson, AB, Harrison, AJ, Distribution of Total Wealth in Britain, Cambridge University Press , Cambridge (1978).
Persky, J., Retrospectives: Pareto's law, Journal of Economic Perspectives 6, 181{192 (1992).
Klass, OS, Biham, O., Levy, M., Malcai, O., Solomon, S., The Forbes 400 and the Pareto wealth distribution, Economics Letters 90, 290{295 (2006).
Hardoon, D., An economy for the 99% , Oxfam GB, Oxfam House, John Smith Drive, Cowley, Oxford, OX4 2JY, UK (January 2017).
Bouchaud, J.-P., M´ezard, M., Wealth condensation in a simple model of economy, Physica A 282, 536{54 (2000).
Dragulescu, A. and Yakovenko, VM, Statistical mechanics of money, Eur. Phys. J. B 17, 723{729 (2000).
Chakraborti, A. and Chakrabarti, BK, Statistical mechanics of money: how saving propensity affects its distribution, Eur. Phys. J. B 17, 167{170 (2000).
Patriarca, M., Chakraborti, A., Germano, G., Influence of saving propensity on the power law tail of wealth distribution, Physica A 369(2), 723{736 (2006).
Scalas, E., Random exchange models and the distribution of wealth. European Physical Journal — Special Topics , 225. pp. 3293-3298. ISSN 1951{6355 (2016).
During, B., Georgiou, N. and Scalas, E., A stylised model for wealth distribution. In Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95{117. ISBN 9789811057045 (2017).
During, Bertram, Georgiou, Nicos and Scalas, Enrico (2017) A stylised model for wealth distribution. In: Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95-117. ISBN 9789811057045
Sinatra, R., Wang, D., Deville, P., Song, C. and Barab´asi, A.-L., Quantifying the evolution of individual scientific impact, Science 354, 6312 (2016).
Einav, L. and Yariv, L., What's in a Surname? The Effects of Surname Initials on Academic Success, Journal of Economic Perspective , Vol. 20, n. 1, p.175{188 (2006).
Ruocco, G., Daraio, C., Folli, V. and Leonetti, M., Bibliometric indicators: the origin of their log-normal distribution and why they are not a reliable proxy for an individual scholar's talent, Palgrave Communications 3:17064 doi: 10.1057/palcomms.2017.64 (2017).
Jurajda, S., Munich, D., Admission to Selective Schools, Alphabetically, Economics of Education Review , Vol. 29, n. 6, p.1100{1109 (2010).
Van Tilburg, WAP, Igou, ER, The impact of middle names: Middle name initials enhance evaluations of intellectual performance, European Journal of Social Psychology , Vol. 44, Issue 4, p.400{411 (2014).
Laham, SM, Koval, P., Alter, AL, The name-pronunciation effect: Why people like Mr. Smith more than Mr. Colquhoun, Journal of Experimental Social Psychology 48, p.752{756 (2012).
Silberzahn, R., Uhlmann, EL, C'est payant d'être Herr Kaiser: les Allemands avec des noms de famille à consonance noble travaillent plus souvent comme gestionnaires, Psychological Science 24 (12): 2437 {44 (2013).
Coffey, B. et McLaughlin, P., De l'avocat au juge: avancement, sexe et appel de nom. Journal électronique SSRN , DOI10.2139 / ssrn.1348280 (2009).
Milanovic, B., Global Inequality of Opportunity: How much of our Income Is Determined by Where We Live?, Review of Economics and Statistics , 97.2 (2015): 452 {60.
Du, Q., Gao, H., Levi, MD, L'effet de l'âge relatif et la réussite professionnelle: témoignages des PDG des entreprises, Economics Letters 117 (3): 660 {662 (2012).
Deaner, RO, Lowen, A., Cobley, S., né au mauvais moment: biais de sélection dans le repêchage de la LNH. PLoS ONE 8 (2): e57753 (2013).
Brooks, D., l'animal social. The Hidden Sources of Love, Character, and Achievement, Random House , 424 p. (2011).
Iacopini, I., Milojevic, S. et Latora, V., Network Dynamics of Innovation Processes, Physical Review Letters 120, 048301 (2018).
Tomasetti, C., Li, L., Vogelstein, B., Divisions des cellules souches, mutations somatiques, étiologie du cancer et prévention du cancer, Science 355, 1330 {1334 (2017).
Newgreen, DF et al., Expansion clonale différentielle dans une population de cellules envahissantes: avantage clonal ou chance muette?, Cellules Tissus Organs 203: 105 {113 (2017).
Snyder, RE et Ellner, SP, We Happy Few: Using Structured Population Models to Identify the Decisive Events in the Lives of Exceptional Individuals, The American Naturalist 188, no. 2 (2016): E28 {E45.
Snyder, RE et Ellner, SP, Pluck or Luck: la variation de caractère ou la chance entraînent-elles une variation du succès de la reproduction à vie?, The American Naturalist 191, no. 4 (2018): E90 {E107.
Taleb N.N., dupe du hasard. Sur le rôle caché du hasard dans les affaires et dans la vie , Mann, Ivanov et Ferber (2018).
Taleb N.N., Black Swan. Sous le signe de l'imprévisibilité , Colibri (2018).
Mauboussin, MJ, The Success Equation: Untangling Skill and Luck in Business, Sports, and Investing, Harvard Business Review Press (2012).
Frank R.H., Success and Fortune. Le facteur de la chance et le mythe de la méritocratie , École supérieure d'économie (2019).
Watts, DJ, tout est évident: une fois que vous connaissez la réponse , Crown Business (2011).
Salganik, MJ, Dodds PS, Watts DJ, étude expérimentale de l'inégalité et de l'imprévisibilité dans un marché culturel artificiel, Science Vol.311 (2006)
Travis, M., Hofman, JM, Sharma, A., Anderson,. A., Watts, DJ, Exploring limits to prediction in complex social systems , Actes de la 25e conférence internationale ACM World Wide Web (2016) arXiv: 1602.01013 [cs.SI]
Stewart, J., The Distribution of Talent, Marilyn Zurmuehlin Working Papers in Art Education 2 : 21-22 (1983).
Sinha, S. et Pan, RK, How a “Hit” Is Born: The Emergence of Popularité from the Dynamics of Collective Choice, In Econophysics and Sociophysics: Trends and Perspectives (éd. BK Chakrabarti, A. Chakraborti et A. Chatterjee), Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Allemagne. doi: 10,1002 / 9783527610006.ch15 (2006).
Fortin, J.-M., Curr, DJ, Big Science contre Little Science: How Scientific Impact Scales with Funding, PLoS ONE 8 (6): e65263 (2013).
Jacob, BA, Lefgren, L., L'impact du financement des subventions de recherche sur la productivité scientifique, Journal of Public Economics 95 (2011) 1168 {1177.
O'Boyle, JR. E. et Aguinis, H., The Best and the Rest: revisiting the norm of normality of individual performance, Personnel Psychology , 65: 79-119. doi: 10.1111 / j.1744-6570.2011.01239.x (2012).
Denrell, J. et Liu, C., Les meilleurs interprètes ne sont pas les plus impressionnants lorsque des performances extrêmes indiquent un manque de fiabilité, Proceedings of the National Academy of Sciences , 109 (24): 9331 {9336 (2012).
Pluchino, A., Rapisarda, A. et Garofalo, C., The Peter principe revisited: A computational study, Physica A 389 (3): 467 {472 (2010).
Pluchino, A., Garofalo, C., Rapisarda, A., Spagano, S. et Caserta, M., Politiciens accidentels: comment les législateurs choisis au hasard peuvent améliorer l'efficacité du parlement, Physica A 390 (21): 3944 {3954 (2011) .
Pluchino, A., Rapisarda, A. et Garofalo, C., Stratégies de promotion efficaces dans les organisations hiérarchiques, Physica A 390 (20): 3496 {3511 (2011).
Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Réduire les avalanches financières par des investissements aléatoires, Phys. Rev. E 88 (6): 062814 (2013).
Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Les stratégies de trading aléatoires sont - elles plus efficaces que les techniques, PLoS One 8 (7): e68344 (2013)
Biondo, AE, Pluchino, A., Rapisarda, A., Le rôle bénéfique des stratégies aléatoires dans les systèmes sociaux et financiers, J. Stat. Phys. 151 (3-4): 607 {622 (2013).
Biondo, AE, Pluchino, A., Rapisarda, A., Avantages micro et macro des investissements aléatoires sur les marchés financiers, Cont. Phys. 55 (4): 318 {334 (2014).
Biondo, AE, Pluchino, A., Rapisarda, A., Modélisation des marchés financiers par la criticité auto-organisée, Phys. Rev. E 92 (4): 042814 (2015).
Wilensky, U., NetLogo. ccl.northwestern.edu/netlogo . Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL (1999).
Merton, RK, The Matthew effect in science, Science 159, 56-63 (1968).
Merton R.K., The Matthew Effect in Science, II: Accumulation of Benefits and Symbolism of Intellectual Property, https://www.hse.ru/data/033/314/1234/3_6_1Merto.pdf .
Bol, T., de Vaan, M. et van de Rijt, A., L'effet Matthew sur le financement des sciences, Actes de la National Academy of Sciences , DOI: 10.1073 / pnas.1719557115 (2018).
Mongeon, P., Brodeur, C., Beaudry, C. et al., La concentration du financement de la recherche entraîne une baisse des rendements marginaux, Évaluation de la recherche 25, 396 {404 (2016).
Merton, RK, Barber, E., The Travels and Adventures of Serendipity , Princeton University Press, Princeton (2004).
Murayama, K. et al., Management of science, serendipity, and performance performance, Research Policy 44 (4), 862 {873 (2015).
Benias, PC et al., Structure et distribution d'un interstitium non reconnu dans les tissus humains, Scientific Reports , vol. 8, 4947 (2018).
Flexner, A, L'utilité des connaissances inutiles , Princeton University Press, Princeton (2017).
Science chanceuse. Les scientifiques annoncent souvent le rôle de la sérendipité dans la recherche. Un projet en Grande-Bretagne vise à tester l'idée populaire avec des preuves. , Nature Editorial, Vol.554, 1er février 2018.
Yaqub, O., Serendipity: Towards a taxonomy and a theory, Research Policy 47, 169 {179 (2018).
Page, SE, le bonus de diversité. How Great Teams Pay Off in the Knowledge Economy , Princeton University Press (2017).
Cimini, G., Gabrielli, A., Sylos Labini, F., La compétitivité scientifique des nations, PLoS ONE 9 (12): e113470. doi.org/10.1371/journal.pone.0113470 (2014).
Curry, S., Allons au-delà de la rhétorique: il est temps de changer notre façon de juger la recherche, Nature 554, 147 (2018).
Nicholson, JM et Ioannidis, JPA, Subventions de recherche: se conformer et être financé, Nature 492, 34 {36 (2012).
Bollen, J., Crandall, D., Junk, D. et al., Un système efficace pour financer la science: de l'examen des propositions aux distributions entre pairs, Scientometrics 110, 521 {528 (2017).
Garner, HR, McIver, LJ et Waitzkin, MB, Financement de la recherche: même travail, deux fois plus d'argent?, Nature 493 599 {601 (2013).

Source: Talent vs Luck: le rôle de l'aléatoire dans le succès et l'échec

Talent contre chance: le rôle du hasard dans le succès et l'échec