Bonjour à tous! Récemment découvert la langue Rust. Il a partagé ses premières impressions dans un article précédent . Maintenant, j'ai décidé de creuser un peu plus, pour cela, vous avez besoin de quelque chose de plus sérieux que la liste. Mon choix s'est porté sur l'arbre Merkle. Dans cet article, je veux:
- parler de cette structure de données
- regardez ce que Rust a déjà
- proposez votre implémentation
- comparer les performances
Arbre Merkle
Il s'agit d'une structure de données relativement simple, et il y a déjà beaucoup d'informations à ce sujet sur Internet, mais je pense que mon article sera incomplet sans une description de l'arbre.
Quel est le problème
L'arbre Merkle a été inventé en 1979, mais a gagné en popularité grâce à la blockchain. La chaîne de blocs dans le réseau est très grande (pour le bitcoin, elle est supérieure à 200 Go), et tous les nœuds ne peuvent pas le pomper. Par exemple, des téléphones ou des caisses enregistreuses. Néanmoins, ils doivent connaître le fait d'inclure telle ou telle transaction dans le bloc. Pour cela, le protocole SPV - Simplified Payment Verification a été inventé.
Comment fonctionne un arbre
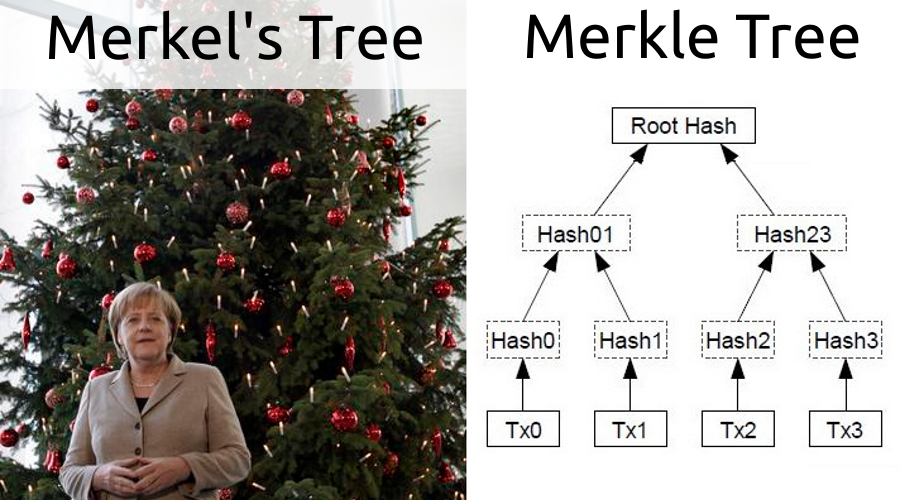
Il s'agit d'un arbre binaire dont les feuilles sont des hachages d'objets. Pour construire le niveau suivant, les hachages des feuilles voisines sont pris par paires, concaténés et le hachage du résultat de la concaténation est calculé, ce qui est illustré dans l'image dans l'en-tête. Ainsi, la racine de l'arbre est un hachage de toutes les feuilles. Si vous supprimez ou ajoutez un élément, la racine changera.
Comment fonctionne un arbre?
Ayant un arbre Merkle, vous pouvez construire des preuves de l'inclusion d'une transaction dans un bloc comme chemin d'un hachage de transaction à la racine. Par exemple, nous nous intéressons à la transaction Tx2, pour cela la preuve sera (Hash3, Hash01). Ce mécanisme est également utilisé dans SPV. Le client télécharge uniquement l'en-tête de bloc avec son hachage. Ayant une transaction d'intérêt, il demande une preuve à un nœud contenant toute la chaîne. Ensuite, il fait un contrôle, pour Tx2 ce sera:
hash(Hash01, hash(Hash2, Hash3)) = Root Hash
Le résultat est comparé à la racine de l'en-tête de bloc. Cette approche rend impossible la fausse preuve, car dans ce cas, le résultat du test ne converge pas avec le contenu de l'en-tête.
Quelles implémentations existent déjà
La rouille est une langue jeune, mais de nombreuses réalisations de l'arbre Merkle y sont déjà écrites. A en juger par Github, actuellement 56, c'est plus qu'en C et C ++ combinés. Bien que Go les fasse tenir debout avec 80 implémentations.
Pour ma comparaison, j'ai choisi cette implémentation par le nombre d'étoiles dans le référentiel.
Cet arbre est construit de la manière la plus évidente, c'est-à-dire qu'il s'agit d'un graphe d'objets. Comme je l'ai déjà noté, cette approche n'est pas complètement compatible avec la rouille. Par exemple, il n'est pas possible d'établir une communication bidirectionnelle entre les enfants et les parents.
La construction des preuves passe par une recherche approfondie. Si une feuille avec le hachage droit est trouvée, le chemin d'accès sera le résultat.
Ce qui peut être amélioré
Ce n'était pas intéressant pour moi de faire une implémentation simple (n + 1), j'ai donc pensé à l'optimisation. Le code de mon arbre vectoriel-merkle est sur Github .
Stockage de données
La première chose qui me vient à l'esprit est de déplacer l'arbre vers un tableau. Cette solution sera bien meilleure en termes de localisation des données: plus de hits de cache et une meilleure précharge. Marcher autour d'objets dispersés dans la mémoire prend plus de temps. Un fait pratique est que tous les hachages ont la même longueur, car calculé par un algorithme. L'arbre Merkle dans le tableau ressemblera à ceci:

Preuve
Lorsque vous initialisez l'arborescence, vous pouvez créer un HashMap avec tous les index de feuille. Ainsi, lorsqu'il n'y a pas de feuille, il n'est pas nécessaire de faire le tour de l'arbre entier, et s'il y en a, vous pouvez immédiatement y aller et vous élever à la racine, en construisant une preuve. Dans mon implémentation, j'ai rendu HashMap facultatif.
Concaténation et hachage
Il semblerait qu'ici peut être amélioré? Après tout, tout est clair - prenez deux hachages, collez-les et calculez un nouveau hachage. Mais le fait est que cette fonction est non commutative, c'est-à-dire hachage (H0, H1) ≠ hachage (H1, H0). Pour cette raison, lors de la construction de la preuve, vous devez vous rappeler de quel côté se trouve le nœud voisin. Cela rend l'algorithme plus difficile à implémenter et ajoute la nécessité de stocker des données redondantes. Tout est très facile à réparer, il suffit de trier les deux nœuds avant de hacher. Par exemple, j'ai cité Tx2, en tenant compte de la commutativité, le chèque ressemblera à ceci:
hash(hash(Hash2, Hash3), Hash01) = Root Hash
Lorsque vous n'avez pas à vous soucier de la commande, l'algorithme de vérification ressemble à une simple convolution d'un tableau:
pub fn validate(&self, proof: &Vec<&[u8]>) -> bool { proof[2..].iter() .fold( get_pair_hash(proof[0], proof[1], self.algo), |a, b| get_pair_hash(a.as_ref(), b, self.algo) ).as_ref() == self.get_root() }
L'élément zéro est le hachage de l'objet souhaité, le premier est son voisin.
C'est parti!
L'histoire serait incomplète sans une comparaison des performances, ce qui m'a pris plusieurs fois plus de temps que la mise en œuvre de l'arbre lui-même. À ces fins, j'ai utilisé le cadre de critères . Les sources des tests eux-mêmes sont ici . Tous les tests ont lieu via l'interface TreeWrapper , qui a été implémentée pour les deux sujets:
pub trait TreeWrapper<V> { fn create(&self, c: &mut Criterion, counts: Vec<usize>, data: Vec<Vec<V>>, title: String); fn find(&self, c: &mut Criterion, counts: Vec<usize>, data: Vec<Vec<V>>, title: String); fn validate(&self, c: &mut Criterion, counts: Vec<usize>, data: Vec<Vec<V>>, title: String); }
Les deux arbres fonctionnent avec la même cryptographie en anneau . Ici, je ne vais pas comparer différentes bibliothèques. J'ai pris le plus commun.
En tant qu'objets de hachage, des chaînes générées de manière aléatoire sont utilisées. Les arbres sont comparés sur des tableaux de différentes longueurs: (500, 1000, 1500, 2000, 2500 3000). 2500 - 3000 est le nombre approximatif de transactions dans le bloc bitcoin pour le moment.
Sur tous les graphiques, l'axe X indique le nombre d'éléments du tableau (ou le nombre de transactions dans le bloc) et l'axe Y représente le temps moyen pour terminer l'opération en microsecondes. C'est-à-dire, plus c'est pire.
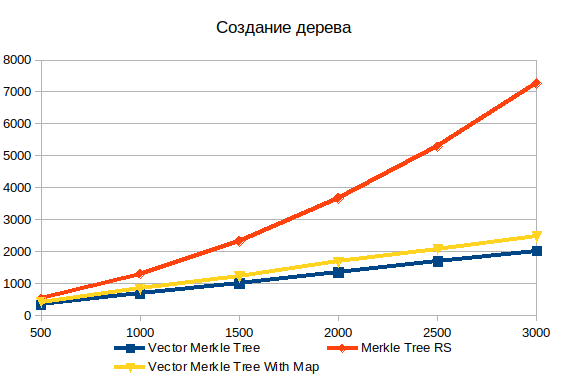
Fabrication d'arbres
Le stockage de toutes les données d'arborescence dans un tableau dépasse largement le graphique de performances des objets. Pour un tableau à 500 éléments, 1,5 fois et pour 3000 éléments déjà 3,6 fois. La nature non linéaire de la dépendance de la complexité au volume des données d'entrée dans l'implémentation standard est clairement visible.
De plus, en comparaison, j'ai ajouté deux variantes de l'arbre vectoriel: avec et sans HashMap . Remplir une structure de données supplémentaire ajoute environ 20%, mais cela vous permet de rechercher des objets beaucoup plus rapidement lors de la création de preuves.
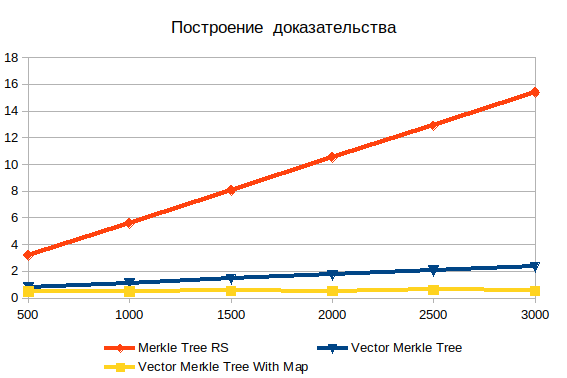
Construire des preuves
Ici, vous pouvez voir l'inefficacité évidente de la recherche en profondeur. Avec une augmentation des intrants, cela ne fait qu'empirer. Il est important de comprendre que les objets que vous recherchez sont des feuilles, donc il ne peut y avoir de complexité log (n) . Si les données sont pré-hachées, le temps de fonctionnement est pratiquement indépendant du nombre d'éléments. Sans hachage, la complexité croît linéairement et consiste en une recherche par force brute.
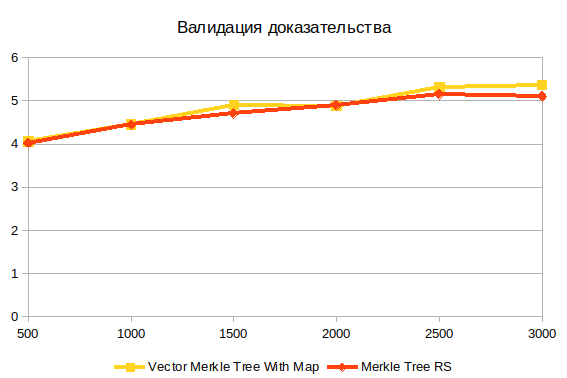
Validation des preuves
Ceci est la dernière opération. Cela ne dépend pas de la structure de l'arbre, car fonctionne avec le résultat de la construction de preuves. Je crois que la principale difficulté ici est le calcul du hachage.
Résumé
- La façon dont les données sont stockées affecte considérablement les performances. Lorsque tout dans un même tableau est beaucoup plus rapide. Et la sérialisation d'une telle structure sera très simple. Le montant total du code est également réduit.
- La concaténation des nœuds avec le tri simplifie considérablement le code, mais ne le rend pas plus rapide.
Un peu de rouille
- J'ai aimé le cadre des critères . Il donne des résultats clairs avec des valeurs moyennes et des écarts équipés de graphiques. Capable de comparer différentes implémentations du même code.
- Le manque d'héritage n'interfère pas beaucoup avec la vie.
- Les macros sont un mécanisme puissant. Je les ai utilisés dans mes tests d'arborescence pour le paramétrage. Je pense que si elles sont mal utilisées, vous pouvez faire une telle chose que vous-même ne serez pas heureux plus tard.
- À certains endroits, le compilateur s'ennuie avec ses vérifications de mémoire. Mon hypothèse initiale selon laquelle commencer à écrire en Rust si simplement ne fonctionnait pas était correcte.
Les références