Je suis tombé sur un
bon article sur la méthode d'estimation spectrale, ce qui est idéal pour un signal court à partir de la somme des harmoniques à faible bruit.
(-copie) Peut-être que mes commentaires aideront le lecteur à comprendre l'essence de la méthode. Ce qui m'a un peu bouleversé, ce sont les capacités incomplètement mises en œuvre de la méthode. La méthode est utilisée pour le radar - pour déterminer rapidement la direction des signaux entrants (angle θ) dans le but ultérieur d'automatiser, il faut le comprendre, l'adaptation du système. Mais - l'auteur ne produit pas de définition numérique de cet angle (et cela est étrange dans son contexte), bien que cette définition soit tout à fait possible. Nous n'avons que de beaux graphiques, selon lesquels, il s'avère, le système doit encore "ramper" et "ramper", déterminant le nombre et l'emplacement des maxima, ce qui n'est pas tout à fait bon.
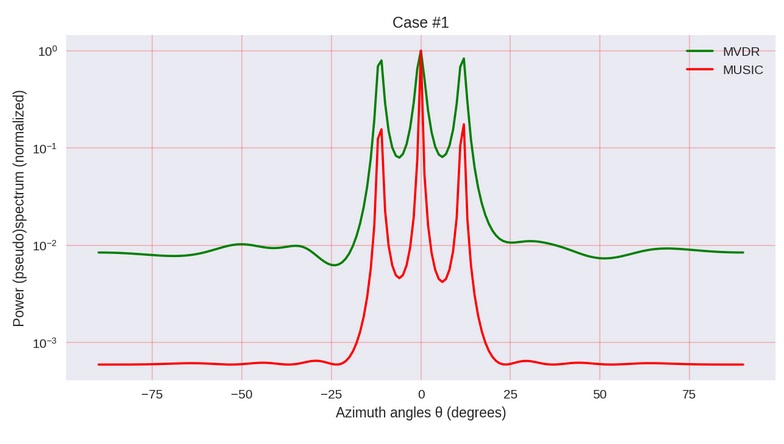Illustration de l'auteur de l'article mentionné"Énoncé du problème"
En bref: nous devons en quelque sorte déterminer d'où (sous quel angle) le signal provient de l'antenne en treillis. Ensuite, pour l'ajuster dans le sens - mais ce n'est plus dans cette «chanson».
«Modélisation du signal reçu»
(ce n'est pas important - apparemment, le "symbole" devrait être lu partout comme un "signal")
Ici, soyez prudent. L'auteur semble travailler avec un certain signal complexe (spatial). Bien que
X , oui, pourrait être, comme écrit, une matrice «d'amplitudes complexes» (dépendant non pas des coordonnées, mais de la fréquence spatiale), mais, par exemple,
XX H sont des «covariances» et non des «densités spectrales».
S est plus similaire à la matrice des «amplitudes complexes», à l'aide de laquelle les composantes harmoniques (signal utile) sont modélisées. Ni les bruits additifs, ni, semble-t-il, même les composantes harmoniques ne sont ici un signal analytique. Bien que les harmoniques, avec des réserves, soient très proches de cela.
"# Formule générale:
# sqrt (N0 / 2) * (G1 + jG2),
# où G1 et G2 sont des processus gaussiens indépendants. »
L'essentiel est de savoir d'où vient la composante imaginaire à partir de mesures réelles, d'une manière ou d'une autre ce n'est pas clair. Il est possible, en principe, de calculer le signal analytique.
Il est possible qu'il existe une «source» où ils ont travaillé avec du vrai
X (signal reçu). Par exemple, l'auteur semble avoir été très désireux de «rendre» les spectres résultants symétriques (pairs) - dans tous les cas considérés, les signaux de test sont donnés par les signaux arrivant symétriquement à gauche et à droite.
"Termes"
Nous avons déterminé la plage d'angles θ d'arrivée du signal, dans laquelle il est logique de regarder. Certes, nous construisons quand même les graphiques pour une raison quelconque de +90 à -90 degrés.
"Un peu de théorie sur la méthode elle-même"
Addition. La MUSIQUE est obtenue par
estimation autorégressive (à partir des équations de Yule-Walker) presque seule, dans le cas où la variance du bruit blanc conditionnel est négligeable. Les résultats sont presque les mêmes. La solution SLAE est même un peu plus économique que la recherche de vecteurs propres, mais, à propos, pour un certain nombre de raisons, la décomposition spectrale de la matrice de covariance avec sa mauvaise conditionnalité serait très souhaitable de toute façon.
EVD, en fait, c'est simplement = "trouver des valeurs et des vecteurs propres", et rien de plus. Pas un algorithme.
Pourquoi écrivons-nous un «pseudo-spectre» - parce que le spectre ne peut être déterminé à partir des vecteurs propres de la matrice de covariance (corrélation) que jusqu'à un facteur d'échelle, c'est-à-dire les valeurs absolues résultantes n'ont pas de sens. Mais nous avons besoin précisément et uniquement de la position des maxima.
- C'est le plus intéressant. Eh bien, tout d'abord, U
0 sont déjà des vecteurs propres, uniquement pour la matrice de covariance - et «enregistrer» sur leur recherche échouera. Ensuite. La recherche de solutions conduira à la nécessité de déterminer les racines de l'équation de puissance, qui est absolument équivalente à une autre décomposition spectrale. L'auteur, apparemment, confond les valeurs propres de matrices complètement différentes.
Mais ... l'essentiel ... maintenant (!), Enfin (!), Nous pourrions logarithmer les racines et déterminer numériquement les «impédances» complexes (pôles modèles) (dans l'équation, c'est encore θ, ce qui n'est pas très bon), qui leur partie imaginaire montrera cet angle même auquel le signal est venu. Il est très regrettable que l'auteur ne l'ait pas fait.
"Modélisation"
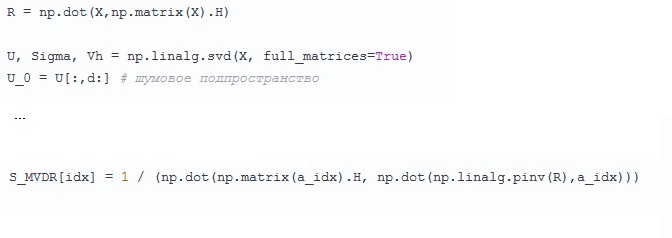
Voici un peu alarmant - au début, la matrice de covariance
R =
XX H a été calculée, qui pour une raison quelconque a été oubliée pendant un certain temps et recommencée à nouveau - décomposée en nombres singuliers et vecteurs
X. Ils ont promis par texte de rechercher les valeurs propres et le vecteur R, qui, bien sûr, est le même, mais pour ainsi dire plus logique, lorsque R a déjà été trouvé. Le problème rencontré par l'auteur n'est pas clair.
Nous rappelons
R lorsque nous évaluons le spectre en utilisant la méthode de dispersion minimale MVDR. Et ici, c'est aussi intéressant -
R , à en juger par le script, semble avoir été inversé, en totale conformité avec cette méthode, de manière classique, sans SVD (pseudo-inversion), bien qu'il semble être de bas rang (très dégénéré). Je veux dire, nos bruits sont-ils si petits? Et bien peut-être.
Vraiment confond ici. La taille du "sous-espace bruit" dans le script semble être attribuée par l'ordre volitif (égal à d). Mais dans le cas réel, nous ne savons pas combien il y a d'harmoniques dans le signal et combien de bruits. Il a fallu analyser ces valeurs propres - lesquelles sont négligeables, qui ne le sont pas.
En général, le travail est très intéressant, et pas seulement pour le radar. La méthode, je crois, a un grand potentiel, juste pour ces types de signaux. L'auteur a très bien fonctionné et certaines incohérences gênantes ne sont pas si difficiles à corriger. Et l'essentiel est de compléter l'article avec la méthode RootMUSIC.