Si vous n'écrivez pas de programme, n'utilisez pas de langage de programmation

Leslie Lamport est l'auteur de l'ouvrage fondamental de l'informatique distribuée, et vous pouvez également le connaître par les lettres La dans La TeX - «Lamport TeX». C'est la première fois qu'il introduit le concept de cohérence cohérente en 1979, et son article «Comment faire un ordinateur multiprocesseur qui exécute correctement des programmes multiprocessus» remporte le prix Dijkstra (plus précisément, en 2000, le prix était appelé à l'ancienne: «PODC Influential Paper Award "). Il y a un article sur Wikipédia à son sujet où vous pouvez obtenir des liens plus intéressants. Si vous êtes ravi de résoudre des problèmes survenus avant ou des problèmes des généraux byzantins (BFT), alors vous devez comprendre que Lamport est derrière tout cela.

Cette habrastatie est une traduction du rapport de Leslie au Heidelberg Laureate Forum en 2018. La conférence se concentrera sur les méthodes formelles utilisées dans le développement de systèmes complexes et critiques tels que la sonde spatiale Rosetta ou les moteurs Amazon Web Services. La visualisation de ce rapport est obligatoire pour assister à une session de questions - réponses que Leslie tiendra à la conférence Hydra - cette habrastatie peut vous faire économiser une heure de temps en regardant une vidéo. Sur cette introduction terminée, nous passons le mot à l'auteur.

Il était une fois, Tony Hoar a écrit: "Chaque grand programme a un petit programme qui essaie de sortir." Je la reformulerais comme ceci: "Dans chaque grand programme, il y a un algorithme qui essaie de sortir." Je ne sais pas, cependant, si Tony serait d'accord avec une telle interprétation.

Prenons, à titre d'exemple, l'algorithme euclidien pour trouver le plus grand diviseur commun de deux entiers positifs $$$(M, N)$ . Dans cet algorithme, nous attribuons $$$x$ valeur $$$M$ , $$$N$ - valeur $$$y$ , puis soustrayez la plus petite de ces valeurs de la plus grande jusqu'à ce qu'elles soient égales. Signification de ces $$$x$ et $$$y$ et sera le plus grand facteur commun. Quelle est la différence essentielle entre cet algorithme et le programme qui le met en œuvre? Dans un tel programme, il y aura beaucoup de choses de bas niveau: $$$M$ et $$$N$ il y aura un certain type, BigInteger ou quelque chose comme ça; il sera nécessaire de déterminer le comportement du programme si $$$M$ et $$$N$ non positif; et ainsi de suite et ainsi de suite. Il n'y a pas de différence claire entre les algorithmes et les programmes, mais au niveau intuitif, nous ressentons la différence - les algorithmes sont plus abstraits, de niveau supérieur. Et, comme je l'ai dit, à l'intérieur de chaque programme réside un algorithme qui essaie de sortir. Habituellement, ce ne sont pas les algorithmes dont on nous a parlé dans le cours d'algorithmes. En règle générale, il s'agit d'un algorithme qui n'est utile que pour ce programme particulier. Le plus souvent, ce sera beaucoup plus compliqué que ceux décrits dans les livres. Ces algorithmes sont souvent appelés spécifications. Et dans la plupart des cas, cet algorithme ne parvient pas à sortir, car le programmeur ne soupçonne pas son existence. Le fait est que cet algorithme ne peut pas être vu si votre réflexion est centrée sur le code, sur les types, les exceptions, les boucles while , etc., et non sur les propriétés mathématiques des nombres. Un programme écrit de cette façon est difficile à déboguer, alors qu'est-ce que cela signifie de déboguer un algorithme au niveau du code. Les outils de débogage sont conçus pour rechercher des erreurs dans le code et non dans l'algorithme. De plus, un tel programme sera inefficace, car, là encore, vous optimiserez l'algorithme au niveau du code.

Comme dans presque tous les autres domaines de la science et de la technologie, ces problèmes peuvent être résolus en les décrivant mathématiquement. Il existe de nombreuses façons de procéder, nous considérerons les plus utiles d'entre elles. Il fonctionne avec des algorithmes séquentiels et parallèles (distribués). Cette méthode consiste à décrire l'exécution de l'algorithme comme une séquence d'états, et chaque état comme l'affectation de propriétés à des variables. Par exemple, l'algorithme euclidien est décrit comme une séquence des états suivants: d'abord, x est affecté à la valeur M (numéro 12) et y est la valeur N (numéro 18). Ensuite, nous soustrayons la plus petite valeur de la plus grande ( $$$x$ de $$$y$ ), ce qui nous amène au prochain état dans lequel nous enlevons déjà $$$y$ de $$$x$ , et l'exécution de l'algorithme s'arrête à ceci: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6], [x \ leftarrow 6, \ leftarrow 6]$ .

Nous appelons une séquence d'états de comportement et une paire d'états consécutifs une étape. Ensuite, tout algorithme peut être décrit par une variété de comportements qui représentent toutes les variantes possibles de l'algorithme. Pour chaque M et N spécifique, il n'y a qu'un seul mode de réalisation, par conséquent, un ensemble d'un comportement est suffisant pour le décrire. Des algorithmes plus complexes, en particulier parallèles, ont beaucoup de comportements.

De nombreux comportements sont décrits, tout d'abord, par un prédicat initial pour les états (un prédicat n'est qu'une fonction avec une valeur booléenne); et, deuxièmement, un prédicat de l'état suivant pour les paires d'états. Certains comportements $$$s_1, s_2, s_3 ...$ n'entre dans de nombreux comportements que si le prédicat initial est vrai pour $$$s_1$ et les prédicats de l'état suivant sont vrais pour chaque étape $$$(s_i, s_ {i + 1})$ . Essayons de décrire l'algorithme euclidien de cette manière. Le prédicat initial ici est: $$$(x = M) \ terrain (y = N)$ . Et le prédicat de l'état suivant pour les paires d'états est décrit par la formule suivante:

Ne vous inquiétez pas, il n'y a que six lignes; il est très facile de les comprendre si vous le faites dans l'ordre. Dans cette formule, les variables sans traits font référence au premier état, et les variables avec traits sont les mêmes variables dans le deuxième état.

Comme vous pouvez le voir, la première ligne indique que dans le premier cas, x est supérieur à y dans le premier état. Après un ET logique, il est indiqué que la valeur de x dans le deuxième état est égale à la valeur de x dans le premier état moins la valeur de y dans le premier état. Après un autre ET logique, il est indiqué que la valeur de y dans le deuxième état est égale à la valeur de y dans le premier état. Tout cela signifie que dans le cas où x est supérieur à y, le programme soustraira y de x et laissera y inchangé. Les trois dernières lignes décrivent le cas où y est supérieur à x. Notez que cette formule est fausse si x est égal à y. Dans ce cas, il n'y a pas d'état suivant et le comportement s'arrête.

Donc, nous venons de décrire l'algorithme euclidien dans deux formules mathématiques - et nous n'avons eu à jouer avec aucun langage de programmation. Quoi de plus beau que ces deux formules? Remplacez-les par une formule. Comportement $$$s_1, s_2, s_3 ...$ est l'exécution de l'algorithme euclidien uniquement si:

• $$$Init_E$ vrai pour $$$s_1$ ,
• $$$Next_E$ vrai pour chaque étape $$$(s_i, s_ {i + 1})$ .

Cela peut être écrit comme un prédicat pour les comportements (nous l'appellerons une propriété) comme suit. La première condition peut être exprimée simplement comme $$$Init_E$ . Cela signifie que nous interprétons un prédicat d'état comme vrai pour le comportement uniquement s'il est vrai pour le premier état. La deuxième condition s'écrit comme suit: $$$\ square Next_E$ . Un carré signifie la correspondance entre les prédicats de paires d'états et les prédicats de comportement, c'est-à-dire $$$Next_E$ vrai pour chaque étape du comportement. Par conséquent, la formule ressemble à ceci: $$$Init_E \ land \ square Next_E$ .

Nous avons donc écrit mathématiquement l'algorithme euclidien. Il s’agit essentiellement de définitions ou d’abréviations de $$$Init_E$ et $$$Next_E$ . Toute cette formule ressemblerait à ceci:

N'est-elle pas belle? Malheureusement, pour la science et la technologie, la beauté n'est pas un critère déterminant, mais cela signifie que nous sommes sur la bonne voie.

La propriété que nous avons notée n'est vraie pour certains comportements que si les deux conditions que nous venons de décrire sont remplies. À $$$M = 12$ et $$$N = 18$ ils sont vrais pour le comportement suivant: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6], [x \ leftarrow 6, \ leftarrow 6]$ . Mais ces conditions sont également remplies pour les versions plus courtes du même comportement: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6]$ . Et nous ne devons pas les prendre en compte, car ce ne sont que des étapes distinctes du comportement que nous avons déjà pris en compte. Il existe un moyen évident de s'en débarrasser: il suffit d'ignorer les comportements qui se terminent dans un état pour lequel au moins une prochaine étape est possible. Mais ce n'est pas la bonne approche, nous avons besoin d'une solution plus générale. De plus, cette condition ne fonctionne pas toujours.

Une discussion de ce problème nous amène aux concepts de sécurité et d'activité. La propriété de sécurité indique quels événements sont valides. Par exemple, l'algorithme est autorisé à renvoyer la valeur correcte. La propriété d'activité indique quels événements doivent se produire tôt ou tard. Par exemple, un algorithme devrait retourner une valeur tôt ou tard. Pour l'algorithme euclidien, la propriété de sécurité est la suivante: $$$Init_E \ land \ square Next_E$ . Une propriété d'activité doit y être ajoutée pour éviter les arrêts prématurés: $$$Init_E \ land \ square Next_E \ land L$ . Dans les langages de programmation, au mieux, il existe une définition primitive de l'activité. Le plus souvent, l'activité n'est même pas mentionnée, cela implique simplement que la prochaine étape du programme doit avoir lieu. Et pour ajouter cette propriété, vous avez besoin d'un code assez complexe. Mathématiquement, il est très facile d'exprimer une activité (juste ce carré est nécessaire pour cela), mais, malheureusement, je n'ai pas le temps pour cela - nous devrons limiter notre discussion à la sécurité.

Une petite digression uniquement pour les mathématiciens: chaque propriété est un ensemble de comportements pour lesquels cette propriété est vraie. Pour chaque ensemble de séquences, il existe une topologie naturelle créée par la fonction de distance suivante:

$$$s = 17, \ sqrt {2}, -2, \ pi, 10, 1/2 \\ t = 17, \ sqrt {2}, -2, e, 10, 1/$

La distance entre ces deux fonctions est de ¼, car la première différence entre elles se situe sur le quatrième élément. En conséquence, plus la portion dans laquelle ces séquences sont identiques est longue, plus elles sont proches les unes des autres. Cette fonction en soi n'est pas si intéressante, mais elle crée une topologie très intéressante. Dans cette topologie, les propriétés de sécurité sont des ensembles fermés et les propriétés d'activité sont des ensembles denses. En topologie, l'un des théorèmes fondamentaux affirme que chaque ensemble est l'intersection d'un ensemble fermé et d'un ensemble dense. Si l'on rappelle que les propriétés sont des ensembles de comportements, il résulte de ce théorème que chaque propriété est une conjonction d'une propriété de sécurité et d'une propriété d'activité. C'est une conclusion qui sera également intéressante pour les programmeurs.

L'exactitude partielle signifie que le programme ne peut s'arrêter que s'il donne la bonne réponse. La justesse partielle de l'algorithme euclidien dit que s'il a terminé l'exécution, alors $$$x = GCD (M, N)$ . Et notre algorithme termine l'exécution si $$$x = y$ . En d'autres termes, $$$(x = y) \ Rightarrow (x = GCD (M, N))$ . La justesse partielle de cet algorithme signifie que cette formule est vraie pour tous les états de comportement. Ajouter un symbole à son début $$$\ carré$ ce qui signifie "pour toutes les étapes". Comme vous pouvez le voir, il n'y a pas de variable avec un trait dans la formule, donc sa vérité dépend du premier état à chaque étape. Et si quelque chose est vrai pour le premier état de chaque étape, cette affirmation est vraie pour tous les états. La justesse partielle de l'algorithme euclidien est satisfaite par tout comportement acceptable pour l'algorithme. Comme nous l'avons vu, le comportement est permis si la formule qui vient d'être donnée est vraie. Lorsque nous disons qu'une propriété est satisfaite, cela signifie simplement que cette propriété découle d'une formule. N'est-ce pas merveilleux? Le voici:

$$$Init_E \ land \ square Next_E \ Rightarrow \ square ((x = y) \ Rightarrow (x = GCD (M, N)))$

Nous passons à l'invariance. Le carré entre crochets après il est appelé la propriété d'invariance :

$$$Init_E \ land \ square Next_E \ Rightarrow \ color {red} {\ square ((x = y) \ Rightarrow (x = GCD (M, N)))}$

La valeur entre crochets après le carré est appelée l' invariant :

$$$Init_E \ land \ square Next_E \ Rightarrow \ square (\ color {red} {(x = y) \ Rightarrow (x = GCD (M, N))})$

Comment prouver l'invariance? Pour prouver $$$Init_E \ land \ square Next_E \ Rightarrow \ square I_E$ , vous devez prouver que pour tout comportement $$$s_1, s_2, s_3 ...$ la conséquence $$$Init_E \ land \ square Next_E$ est la vérité $$$I_e$ pour toute condition $$$s_j$ . Nous pouvons le prouver par induction, pour cela nous devons prouver ce qui suit:

1. de $$$Init_E \ land \ square Next_E$ il s'ensuit que $$$I_e$ vrai pour l'état $$$s_1$ ;
2. de $$$Init_E \ land \ square Next_E$ il s'ensuit que si $$$I_e$ vrai pour l'état $$$s_j$ alors c'est aussi
   vrai pour l'état $$$s_ {j + 1}$ .

Nous devons d'abord prouver que $$$Init_E$ implique $$$I_e$ . Parce que la formule prétend que $$$Init_E$ vrai pour le premier état, cela signifie que $$$I_e$ vrai pour le premier état. De plus, lorsque $$$Next_E$ vrai pour n'importe quelle étape, et $$$I_e$ fidèle à $$$s_j$ , $$$I_e$ vrai pour $$$s_ {j + 1}$ parce que $$$\ square Next_E$ signifie que $$$Next_E$ vrai pour n'importe quelle paire d'états. Ceci est écrit comme ceci: $$$Next_E \ land I_E \ Rightarrow I'_E$ où $$$I'_E$ Est-ce $$$I_e$ pour toutes les variables avec un trait.

Un invariant qui remplit les deux conditions que nous venons de prouver est appelé invariant inductif . L'exactitude partielle n'est pas inductive. Pour prouver son invariance, vous devez trouver l'invariant inductif qui l'implique. Dans notre cas, l'invariant inductif sera le suivant: $$$GCD (x, y) = GCD (M, N)$ .

Chaque action ultérieure de l'algorithme dépend de son état actuel et non des actions passées. L'algorithme satisfait la propriété de sécurité, car l'invariant inductif y est conservé. L'algorithme euclidien peut calculer le plus grand dénominateur commun (c'est-à-dire qu'il ne s'arrête pas jusqu'à ce qu'il soit atteint) car il a un invariant $$$GCD (x, y) = GCD (M, N)$ . Pour comprendre l'algorithme, vous devez connaître son invariant inductif. Si vous avez étudié la vérification des programmes, vous savez que la preuve de l'invariant qui vient d'être donné n'est rien de plus qu'une méthode pour prouver l'exactitude partielle des programmes séquentiels de Floyd-Hoare. Vous avez peut-être également entendu parler de la méthode Hoviki - Gris , qui est l'extension de la méthode Floyd-Hoar aux programmes parallèles. Dans les deux cas, l'invariant inductif est écrit en utilisant l'annotation du programme. Et si vous le faites à l'aide des mathématiques, et non avec un langage de programmation, cela se fait extrêmement simplement. C'est ce qui est au cœur de la méthode Hoviki Gris. Les mathématiques rendent les phénomènes complexes beaucoup plus accessibles à la compréhension, bien que les phénomènes eux-mêmes, bien sûr, ne deviendront pas plus simples.

Examinez de plus près les formules. Si en mathématiques, nous avons écrit une formule avec des variables $$$x$ et $$$y$ , cela ne signifie pas que d'autres variables n'existent pas. Vous pouvez ajouter une autre équation dans laquelle $$$y$ placé par rapport à $$$z$ , cela ne changera rien. La formule ne dit rien sur les autres variables. J'ai déjà dit qu'un état est une affectation de valeurs à des variables, maintenant vous pouvez ajouter à cela: avec toutes les variables possibles, en commençant $$$x$ et $$$y$ et se terminant avec la population de l'Iran. Je dois avouer: quand j'ai dit que la formule $$$Init_E \ land \ square Next_E$ décrit l'algorithme euclidien, j'ai menti. Il décrit en fait un univers dans lequel les significations $$$x$ et $$$y$ représentent l'exécution de l'algorithme euclidien. La deuxième partie de la formule ( $$$\ square Next_E$ ) prétend que chaque étape change $$$x$ ou $$$y$ . En d'autres termes, il décrit un univers dans lequel la population iranienne ne peut changer que si le sens a changé $$$x$ ou $$$y$ . Il s'ensuit qu'en Iran, personne ne peut naître une fois l'exécution de l'algorithme euclidien terminée. De toute évidence, ce n'est pas le cas. Cette erreur peut être corrigée si nous avons des étapes valides pour lesquelles $$$x$ et $$$y$ restent inchangés. Par conséquent, nous devons ajouter une partie supplémentaire à notre formule: $$$Init_E \ land \ square (Next_E \ lor (x '= x) \ land (y' = y))$ . Par souci de concision, nous l'écrivons comme ceci: $$$Init_E \ land \ square [Next_E] _ {<x, y>}$ . Cette formule décrit un univers contenant l'algorithme euclidien. Les mêmes modifications doivent être apportées à la preuve de l'invariant:

• Nous prouvons: $$$Init_E \ land \ color {red} {\ square [Next_E] _ {<x, y>}} \ Rightarrow \ square I_E$
• Avec l'aide de:
  
  1. $$$Init_E \ Rightarrow I_E$
  2. $$$\ color {red} {\ square [Next_E] _ {<x, y>}} \ land I_E \ Rightarrow I'_E$

Ce changement est responsable de la sécurité de l'algorithme euclidien, car maintenant des comportements sont possibles dans lesquels les valeurs $$$x$ et $$$y$ ne change pas. Ces comportements doivent être éliminés à l'aide de la propriété d'activité. C'est assez simple, mais je n'en parlerai pas maintenant.

Parlez de mise en œuvre. Supposons que nous ayons une sorte de machine qui implémente l'algorithme euclidien comme un ordinateur. Il représente les nombres sous forme de tableaux de mots de 32 bits. Pour les opérations simples d'addition et de soustraction, elle a besoin de plusieurs étapes, comme un ordinateur. Si vous ne touchez pas encore à l'activité, nous pouvons également imaginer une telle machine par la formule $$$Init_ {ME} \ land \ square [Next_ {ME}] _ {<...>}$ . Que voulons-nous dire lorsque nous disons que la machine euclidienne implémente l'algorithme euclidien? Cela signifie que la formule suivante est correcte:

Ne vous inquiétez pas, nous allons maintenant l'examiner dans l'ordre. Il dit que notre machine satisfait certaines propriétés ( $$$\ Rightarrow$ ) Cette propriété est la formule euclidienne. $$$(Init_E \ land \ square [Next_E] _ {<x, y>}$ , les points sont des expressions qui contiennent des variables machine euclidiennes, et $$$AVEC$ Est une substitution. En d'autres termes, la deuxième ligne est la formule euclidienne dans laquelle $$$x$ et $$$y$ remplacé par des points. En mathématiques, il n'y a pas de notation universellement acceptée pour la substitution, j'ai donc dû la créer moi-même. Essentiellement, la formule euclidienne ( $$$Init_E \ land \ square [Next_E] _ {<x, y>}$ ) Est une abréviation de la formule:

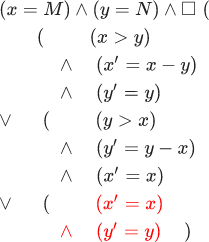
Partie rouge surlignée de la formule, permettant $$$x$ et $$$y$ dans $$$(Init_E \ land \ square [Next_E] _ {\ color {red} {<x, y>}}$ reste le même.

L'expression décrite indique non seulement que la machine implémente l'algorithme euclidien, mais également qu'elle le fait en tenant compte des substitutions spécifiées. Si vous prenez simplement quelques programmes et dites que les variables de ces programmes sont liées à $$$x$ et $$$y$ - cela n'a aucun sens de dire que tout cela "implémente l'algorithme euclidien". Il est nécessaire d'indiquer exactement comment l'algorithme sera implémenté, pourquoi, après toutes les permutations, la formule deviendra vraie. Maintenant, je n'ai pas le temps de montrer que la définition décrite ci-dessus est correcte, vous devez me croire sur parole. Mais vous, je pense, avez déjà apprécié sa simplicité et son élégance. Le calcul est vraiment beau - avec lui, nous avons pu déterminer ce que signifie qu'un algorithme en implémente un autre.

Pour le prouver, il est nécessaire de trouver un invariant adapté $$$I_ {ME}$ Voitures euclidiennes. Pour ce faire, les conditions suivantes doivent être remplies:

1. $$$Init_ {ME} \ Rightarrow (Init_E, WITH \ thinspace x \ leftarrow ..., y \ leftarrow ...)$
2. $$$I_ {ME} \ land [Next_ {ME}] _ {<...>} \ Rightarrow ([Next_E] _ {<x, y>}, WITH \ thinspace x \ leftarrow ..., y \ leftarrow. ..)$

Nous ne nous attarderons pas sur eux maintenant, il suffit de prêter attention au fait que ce sont des formules mathématiques ordinaires, mais pas les plus simples. Invariant $$$I_ {ME}$ explique pourquoi la machine euclidienne implémente l'algorithme euclidien. La mise en œuvre signifie remplacer les expressions par des variables. Il s'agit d'une opération mathématique très courante. Mais dans le programme, une telle substitution ne peut pas être effectuée. Vous ne pouvez pas remplacer a + b à la place de x dans l'expression d'affectation x = … , un tel enregistrement n'aura pas de sens. Alors, comment déterminer qu'un programme en implémente un autre? Si vous ne pensez qu'en termes de programmation, ce n'est pas possible. Dans le meilleur des cas, vous pouvez trouver une définition délicate, mais une bien meilleure façon est de traduire les programmes en formules mathématiques et d'utiliser la définition que j'ai donnée ci-dessus. Traduire un programme en une formule mathématique, c'est donner la sémantique du programme. Si la machine euclidienne est un programme, et $$$Init_ {ME} \ land \ square [Next_ {ME}] _ {<...>}$ - sa notation mathématique, puis $$$(Init_E \ land \ square [Next_E] _ {<x, y>}, WITH \ thinspace x \ leftarrow ..., y \ leftarrow ...)$ nous montre que cela signifie que "le programme implémente l'algorithme euclidien". Les langages de programmation sont très complexes, donc cette traduction du programme en langage mathématique est également compliquée, donc en pratique nous ne le faisons pas. Simplement, les langages de programmation ne sont pas conçus pour écrire des algorithmes dessus. , , , : , x y , . , , , .

- : , , , . , . — . . , . , — , . :

. $$$DecrementX$ :

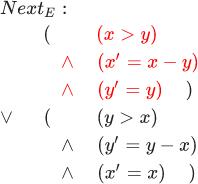
— $$$DecrementY$ :

, :

.

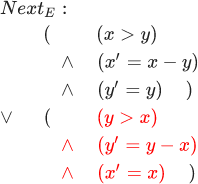
. Rosetta — , . Virtuoso. . TLA+, . , , . , (Eric Verhulst), . , TLA+, : « TLA+ . - C. TLA+ Virtuoso». . . , , , . . TLA+. , .

. Communications of the ACM ] , - Amazon . Amazon Web Services — , Amazon. , — TLA+. . -, , . , , . -, , . , — , , . -, , Amazon , . , 10% TLA+.

— Microsoft. TLA+ 2004 . 2015 TLA+, . . Amazon Web Services. Microsoft , , . : « , ». , Microsoft - . : « ». 2016-17 . TLA+, 150 , Azure ( Microsoft). Azure 2018 , , . : « , . , ». , , . - : , . , , .

, TLA+ . , TLA+, TLA+ Azure, , TLA+. , . , TLA+ , . Microsoft Cosmos DB, , . , . TLA+, , , TLA+.

TLA+ — . . TLA+ . , , . TLA+ , . : TLA+ , .

, . , , . , . Amazon Microsoft , . , .

, . — , . , Hydra 2019, 11-12 2019 -. .