👨🏼‍🔧 👨🏽‍🤝‍👨🏻 👨🏾‍🏭 Filtrage linéaire optimal: de la descente de gradient aux filtres adaptatifs 🐧 🎑 🤕

Développer le sujet des résumés dans la spécialité du master "Communication et traitement du signal" (TU Ilmenau), je voudrais poursuivre l'un des principaux sujets du cours "Traitement adaptatif et matriciel du signal" . À savoir, les bases du filtrage adaptatif.

Pour qui cet article a été écrit pour la première fois:

1) pour une confrérie étudiante d'une spécialité autochtone ;
2) pour les enseignants qui préparent des séminaires pratiques, mais n'ont pas encore décidé des outils - voici des exemples en python et Matlab / Octave ;
3) pour toute personne intéressée par le sujet du filtrage.

Que peut-on trouver sous la coupe:

1) des informations issues de la théorie, que j'ai essayé d'organiser de manière aussi concise que possible, mais, me semble-t-il, informative;
2) exemples d'utilisation de filtres: notamment dans le cadre de l'égaliseur du réseau d'antennes;
3) des liens vers la littérature de base et les bibliothèques ouvertes (en python), qui peuvent être utiles pour la recherche.

En général, bienvenue et trions tout par points.

La personne pensive sur la photo est familière à beaucoup, je pense, Norbert Wiener. Pour la plupart, nous étudierons le filtre de son nom. Cependant, on ne peut pas ne pas mentionner notre compatriote - Andrei Nikolaevich Kolmogorov, dont l' article de 1941 a également apporté une contribution significative au développement de la théorie du filtrage optimal, qui même dans les sources anglaises est appelée la théorie du filtrage Kolmogorov-Wiener .

Que pensons-nous?

Aujourd'hui, nous envisageons un filtre classique à réponse impulsionnelle finie (FIR, réponse impulsionnelle finie), qui peut être décrit par le circuit simple suivant (Fig. 1).

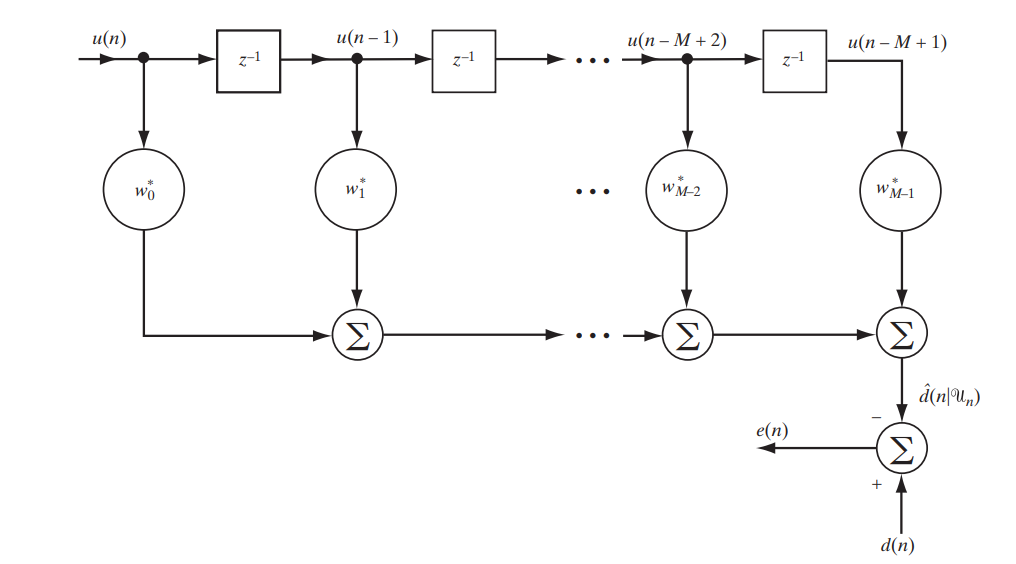
Fig.1. Le schéma de filtrage FIR pour étudier le filtre de Wiener [1. p.117]

Nous écrirons sous forme matricielle ce qui sera exactement à la sortie de ce stand:

$e (n) = d (n) - \ hat {d} (n | \ mathcal {U} _n) = d (n) - \ mathbf {w} ^ H \ mathbf {u} \ qquad (1)$

Déchiffrez la notation:

Est la différence (erreur) entre les signaux donnés et reçus
Est un signal prédéfini
$\ mathbf {u}$ Est un vecteur d'échantillons ou, en d'autres termes, un signal à l'entrée du filtre
$\ hat {d} (n | \ mathcal {U} _n)$ Le signal est-il à la sortie du filtre
$\ mathbf {w} ^ H$ - c'est une conjugaison hermitienne du vecteur de coefficient de filtre - c'est dans leur sélection optimale que réside l'adaptabilité du filtre

Vous avez probablement déjà deviné que nous nous efforcerons de rechercher la plus petite différence entre le signal donné et le signal filtré, c'est-à-dire la plus petite erreur. Cela signifie que nous sommes confrontés à une tâche d'optimisation.

Qu'allons-nous optimiser?

Pour optimiser, ou plutôt minimiser, nous ne signifierons pas seulement l' erreur, l' erreur quadratique moyenne ( MSE - Mean Sqared Error ):

$MSE: J (\ mathbf {w}) = E \ {e (n) ^ 2 \} \ qquad (2)$

où $J (\ mathbf {w})$ désigne la fonction de coût du vecteur de coefficients de filtre, et $E \ {* \}$ désigne le mat. en attente.

Le carré dans ce cas est très agréable, car cela signifie que nous sommes confrontés au problème de la programmation convexe (je n'ai recherché qu'un tel analogue de l' optimisation convexe anglaise), ce qui, à son tour, implique un seul extremum (dans notre cas, un minimum).

Fig.2. La surface de l'erreur quadratique moyenne .

Notre fonction d'erreur a une forme canonique [1, p. 121]:

$J (\ mathbf {w}) = \ sigma ^ 2_d - \ mathbf {w} ^ H \ mathbf {p} - \ mathbf {p} ^ H \ mathbf {w} + \ mathbf {w} ^ H \ mathbf { R} \ mathbf {w} \ qquad (3)$

où $\ sigma ^ 2_d$ Est la variance du signal attendu, $\ mathbf {p} = E \ {\ mathbf {u} (n) d ^ * (n) \}$ Est le vecteur de corrélation croisée entre le vecteur d'entrée et le signal attendu, et $\ mathbf {R} = E \ {\ mathbf {u} (n) \ mathbf {u} ^ H (n) \}$ Est la matrice d'autocorrélation du signal d'entrée.

La conclusion de cette formule est là (je l'ai essayée plus clairement).

Comme nous l'avons noté ci-dessus, si nous parlons de programmation convexe, nous aurons alors un extremum (minimum). Ainsi, pour trouver la valeur minimale de la fonction de coût (l'erreur quadratique moyenne minimale), il suffit de trouver la tangente de la pente de la tangente ou, en d'autres termes, la dérivée partielle par rapport à notre variable étudiée:

$\ frac {\ delta J (\ mathbf {w})} {\ delta w ^ *} = - \ mathbf {p} + \ mathbf {R} \ mathbf {w} \ qquad (4)$

Dans le meilleur des cas ( $\ mathbf {w} = \ mathbf {w} _ {opt}$ ), l'erreur devrait, bien sûr, être minimale, ce qui signifie que nous assimilons la dérivée à zéro:

$\ mathbf {R} \ mathbf {w} _ {opt} = \ mathbf {p} \ qquad (5)$

En fait, le voici, notre poêle, à partir duquel nous danserons plus loin: devant nous est un système d'équations linéaires .

Comment allons-nous décider?

Il convient de noter tout de suite que les deux solutions, que nous examinerons ci-dessous, dans ce cas sont théoriques et pédagogiques, puisque $\ mathbf {R}$ et $\ mathbf {p}$ connu à l'avance (c'est-à-dire que nous avions la capacité présumée de collecter suffisamment de statistiques pour les calculer). Cependant, l'analyse de tels exemples simplifiés est la meilleure à laquelle vous pouvez penser pour comprendre les approches de base.

Solution analytique

Ce problème peut être résolu, pour ainsi dire, dans le front - en utilisant des matrices inverses:

$\ mathbf {w} _ {opt} = \ mathbf {R} ^ {- 1} \ mathbf {p} \ qquad (6)$

Une telle expression est appelée l' équation de Wiener-Hopf - elle nous sert encore de référence.

Bien sûr, pour être complètement méticuleux, il serait probablement plus correct d'écrire ce cas de manière générale, c'est-à-dire pas avec $^ {-}$ , et avec ( pseudo-inversion ):
$\ mathbf {R} ^ + = \ mathbf {R} ^ H (\ mathbf {R} \ mathbf {R} ^ H) ^ {- 1}$

Cependant, la matrice d'autocorrélation ne peut pas être non carrée ou singulière, donc, à juste titre, nous pensons qu'il n'y a pas de contradiction.

De cette équation, il est analytiquement possible de déduire ce que la valeur minimale de la fonction de coût sera égale (c'est-à-dire, dans notre cas MMSE - erreur quadratique moyenne minimale):

$J_ {min} = J (\ mathbf {w} _ {opt}) = \ sigma ^ 2_d - \ mathbf {p} ^ H \ mathbf {R} ^ {- 1} \ mathbf {p} \ qquad (7)$

La dérivation de la formule est là (j'ai aussi essayé de colorer plus coloré).

Eh bien, il y a une solution.

Solution itérative

Cependant, oui, il est possible de résoudre un système d'équations linéaires sans inverser la matrice d'autocorrélation - de manière itérative ( pour économiser les calculs ). À cette fin, considérons la méthode native et compréhensible de descente à gradient ( méthode de descente la plus raide / à gradient ).

L'essence de l'algorithme peut être réduite à ce qui suit:

Nous définissons la variable souhaitée sur une valeur par défaut (par exemple, $\ mathbf {w} (0) = \ mathbf {0}$ )
Choisissez une étape $\ mu$ (comment exactement nous choisissons, nous parlerons ci-dessous).
Et puis, pour ainsi dire, nous descendons le long de notre surface d'origine (dans notre cas, c'est la surface MSE) avec une étape donnée $\ mu$ et une certaine vitesse déterminée par l'amplitude du gradient.

D'où le nom: gradient - gradient ou plus raide - descente pas à pas - descente.

Le gradient dans notre cas est déjà connu: en fait, nous l'avons trouvé en différenciant la fonction de coût (la surface est concave, comparer avec [1, p. 220]). Nous écrivons à quoi ressemblera la formule de mise à jour itérative de la variable souhaitée (coefficients de filtre) [1, p. 220]:

$\ mathbf {w} (n + 1) = \ mathbf {w} (n) - \ mu [- \ mathbf {p} + \ mathbf {R} \ mathbf {w} (n)] \ qquad (8)$

où Est le numéro d'itération.

Parlons maintenant du choix d'une taille de pas.

Nous listons les prémisses évidentes:

l'étape ne peut pas être négative ou nulle
le pas ne doit pas être trop grand, sinon l'algorithme ne convergera pas (il va, pour ainsi dire, sauter de bord en bord, sans tomber dans l'extrême)
l'étape, bien sûr, peut être très petite, mais ce n'est pas non plus entièrement souhaitable - l'algorithme passera plus de temps

Concernant le filtre de Wiener, des restrictions ont bien sûr déjà été trouvées il y a longtemps [1, p. 222-226]:

$0 <\ mu <\ frac {2} {\ lambda_ {max}} \ qquad (9)$

où $\ lambda_ {max}$ Est la plus grande valeur propre de la matrice d'autocorrélation $\ mathbf {R}$ .

Soit dit en passant, les valeurs propres et les vecteurs sont un sujet intéressant distinct dans le contexte du filtrage linéaire. Il existe même un filtre propre complet pour ce cas (voir l'annexe 1).

Mais ce n'est heureusement pas tout. Il existe également une solution adaptative optimale:

$\ mu (n) = \ frac {\ mathbf {\ gamma} (n) ^ H \ mathbf {\ gamma} (n)} {\ mathbf {\ gamma} (n) ^ H \ mathbf {R} \ mathbf { \ gamma} (n)} \ qquad (10)$

où $\ mathbf {\ gamma} (n) = \ mathbf {p} - \ mathbf {R} \ mathbf {w} (n)$ Est un gradient négatif. Comme le montre la formule, l'étape est recalculée à chaque itération, c'est-à-dire qu'elle s'adapte.

La conclusion de la formule est ici (beaucoup de mathématiques - ne regardez que les mêmes nerds notoires comme moi).

D'accord, pour la deuxième décision, nous avons également préparé le terrain.

Mais est-ce possible avec des exemples?

Par souci de clarté, nous allons effectuer une petite simulation. Nous utiliserons Python 3.6.4 .

Je dirai tout de suite que ces exemples font partie de l'un des devoirs, chacun étant proposé aux étudiants pour solution dans les deux semaines. J'ai réécrit la partie sous python (afin de vulgariser le langage auprès des ingénieurs radio). Peut-être que vous rencontrerez d'autres options sur le Web d'autres anciens élèves.

import numpy as np import matplotlib.pyplot as plt from scipy.linalg import toeplitz def convmtx(h,n): return toeplitz(np.hstack([h, np.zeros(n-1)]),\ np.hstack([h[0], np.zeros(n-1)])) def MSE_calc(sigmaS, R, p, w): w = w.reshape(w.shape[0], 1) wH = np.conj(w).reshape(1, w.shape[0]) p = p.reshape(p.shape[0], 1) pH = np.conj(p).reshape(1, p.shape[0]) MSE = sigmaS - np.dot(wH, p) - np.dot(pH, w) + np.dot(np.dot(wH, R), w) return MSE[0, 0] def mu_opt_calc(gamma, R): gamma = gamma.reshape(gamma.shape[0], 1) gammaH = np.conj(gamma).reshape(1, gamma.shape[0]) mu_opt = np.dot(gammaH, gamma) / np.dot(np.dot(gammaH, R), gamma) return mu_opt[0, 0]

Nous utiliserons notre filtre linéaire pour le problème d' égalisation de canal , dont le but principal est de niveler les différents effets de ce canal sur le signal utile.

Le code source peut être téléchargé dans un fichier ici ou ici (oui, j'avais un tel passe-temps - éditer Wikipedia).

Modèle de système

Supposons qu'il existe un réseau d'antennes (nous l'avons déjà examiné dans un article sur la MUSIQUE ).

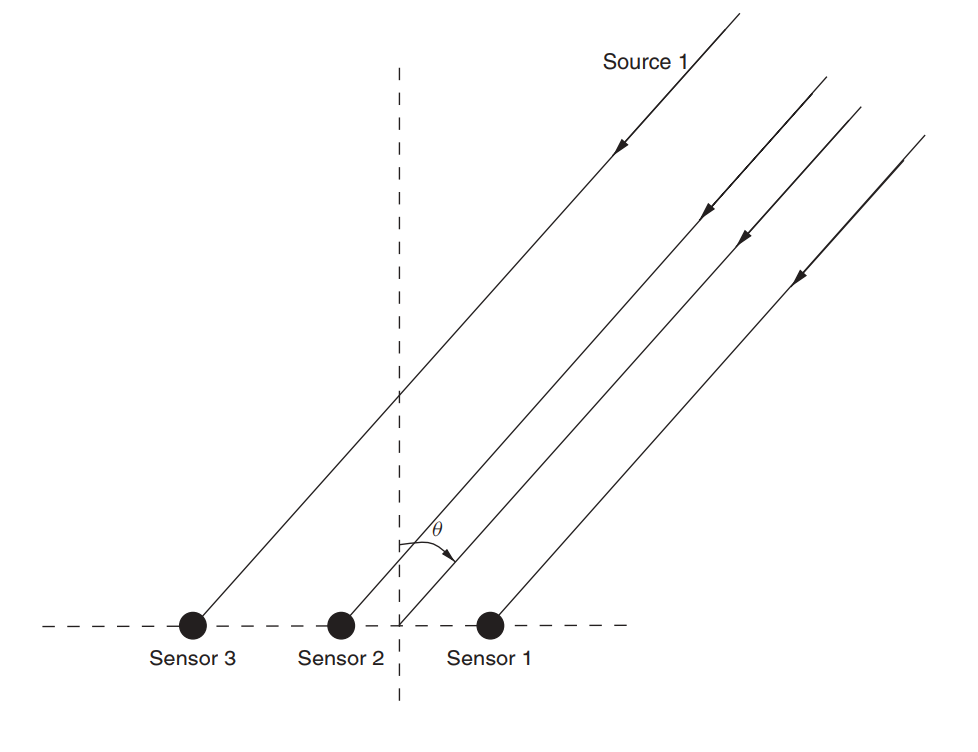
Fig. 3. Réseau d'antennes linéaires non directionnelles (ULAA - réseau d'antennes linéaires uniformes) [2, p. 32].

Définissez les paramètres initiaux du réseau:

 M = 5 #    (number of sensors)

Dans cet article, nous considérerons quelque chose comme un canal à large bande avec évanouissement , dont une caractéristique est la propagation par trajets multiples . Pour de tels cas, une approche est généralement appliquée dans laquelle chaque faisceau est modélisé en utilisant un retard d'une certaine amplitude (Fig. 4).

Fig. 4. Le modèle du canal large bande avec n retards fixes [3, p. 29]. Comme vous le comprenez, les désignations spécifiques ne jouent aucun rôle - dans ce qui suit, nous utiliserons des désignations légèrement différentes.

Le modèle du signal reçu pour un capteur est exprimé comme suit:

$x (n) = \ sum_ {l = 0} ^ Lh (l) s (n-l) + \ nu (n)$

Dans ce cas indique le numéro de référence, h (l) Est la réponse du canal le long du l- ème faisceau, L est le nombre de registres de retard, s est le signal (utile) transmis, $\ nu (n)$ - bruit additif.

Pour plusieurs capteurs, la formule prendra la forme:

$\ mathbf {x} (n) = \ mathbf {H} \ mathbf {s} (n) + \ mathbf {\ nu} (n)$

où $\ mathbf {x} (n)$ et $\ mathbf {\ nu} (n)$ - avoir une dimension $M \ fois 1$ dimension $\ mathbf {H}$ est égal à $M \ fois (M-L)$ et la dimension $\ mathbf {s} (n)$ est égal $(M-L) \ fois 1$ .

Supposons que chaque capteur reçoive également un signal avec un certain retard, en raison de l'incidence de l'onde à un angle. Matrix $\ mathbf {H}$ dans notre cas, il s'agira d'une matrice convolutionnelle pour le vecteur de réponse de chaque rayon. Je pense que le code sera plus clair:

 h = np.array([0.722-1j*0.779, -0.257-1j*0.722, -0.789-1j*1.862]) L = len(h)-1 # number of signal sources H = convmtx(h,ML) print(H.shape) print(H)

La conclusion sera:

 >>> (5, 3) >>> array([[ 0.722-0.779j, 0. +0.j , 0. +0.j ], [-0.257-0.722j, 0.722-0.779j, 0. +0.j ], [-0.789-1.862j, -0.257-0.722j, 0.722-0.779j], [ 0. +0.j , -0.789-1.862j, -0.257-0.722j], [ 0. +0.j , 0. +0.j , -0.789-1.862j]])

Ensuite, nous définissons les données initiales pour le signal et le bruit utiles:

 sigmaS = 1 #    (the signal's s(n) power) sigmaN = 0.01 #   (the noise's n(n) power)

Passons maintenant aux corrélations.

 Rxx = (sigmaS)*(np.dot(H,np.matrix(H).H))+(sigmaN)*np.identity(M) p = (sigmaS)*H[:,0] p = p.reshape((len(p), 1))

La dérivation des formules ici (aussi une feuille pour les plus désespérés).

Nous trouvons une solution pour Wiener:

 # Solution of the Wiener-Hopf equation: wopt = np.dot(np.linalg.inv(Rxx), p) MSEopt = MSE_calc(sigmaS, Rxx, p, wopt)

Passons maintenant à la méthode de descente en gradient.

Trouvez la plus grande valeur propre afin que la limite supérieure de l'étape puisse en être dérivée (voir formule (9)):

 lamda_max = max(np.linalg.eigvals(Rxx))

Maintenant, définissons un tableau d'étapes qui représentera une certaine fraction du maximum:

 coeff = np.array([1, 0.9, 0.5, 0.2, 0.1]) mus = 2/lamda_max*coeff # different step sizes

Définissez le nombre maximum d'itérations:

 N_steps = 100

Exécutez l'algorithme:

 MSE = np.empty((len(mus), N_steps), dtype=complex) for mu_idx, mu in enumerate(mus): w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): w = w - mu*(np.dot(Rxx, w) - p) MSE[mu_idx, N_i] = MSE_calc(sigmaS, Rxx, p, w)

Maintenant, nous ferons de même, mais pour l'étape adaptative (formule (10)):

 MSEoptmu = np.empty((1, N_steps), dtype=complex) w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): gamma = p - np.dot(Rxx,w) mu_opt = mu_opt_calc(gamma, Rxx) w = w - mu_opt*(np.dot(Rxx,w) - p) MSEoptmu[:, N_i] = MSE_calc(sigmaS, Rxx, p, w)

Vous devriez obtenir quelque chose comme ceci:

Dessin

 x = [i for i in range(1, N_steps+1)] plt.figure(figsize=(5, 4), dpi=300) for idx, item in enumerate(coeff): if item == 1: item = '' plt.loglog(x, np.abs(MSE[idx, :]),\ label='$\mu = '+str(item)+'\mu_{max}$') plt.loglog(x, np.abs(MSEoptmu[0, :]),\ label='$\mu = \mu_{opt}$') plt.loglog(x, np.abs(MSEopt*np.ones((len(x), 1), dtype=complex)),\ label = 'Wiener solution') plt.grid(True) plt.xlabel('Number of steps') plt.ylabel('Mean-Square Error') plt.title('Steepest descent') plt.legend(loc='best') plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()

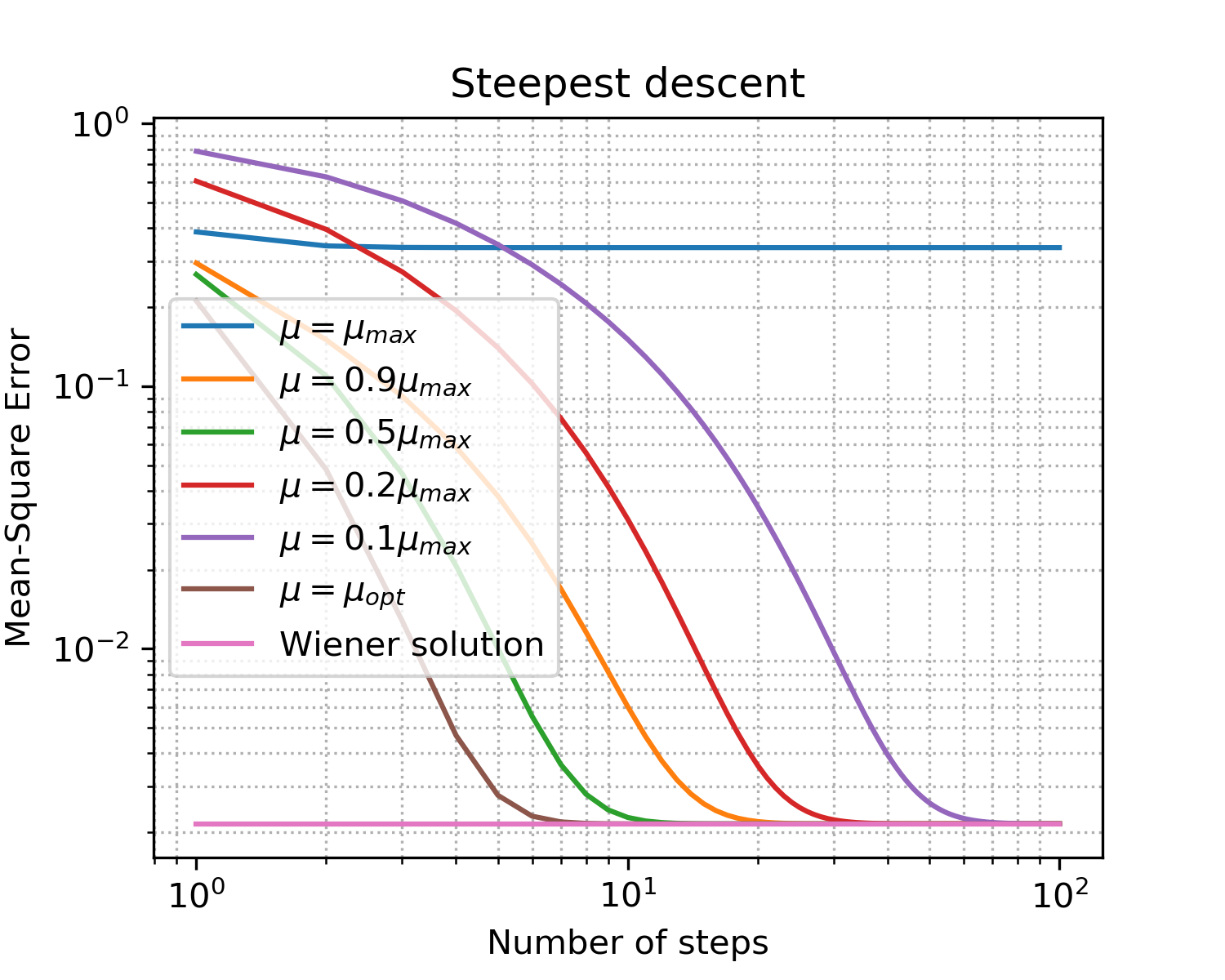
Fig. 5. Courbes d'apprentissage pour les étapes de différentes tailles.

Fixations pour énoncer les principaux points de la descente en pente:

comme prévu, l'étape optimale donne la convergence la plus rapide;
ne signifie plus mieux: après avoir dépassé la limite supérieure, nous n'avons pas du tout atteint la convergence.

Nous avons donc trouvé le vecteur optimal de coefficients de filtre qui égalisera le mieux les effets du canal - nous avons formé l'égaliseur .

Y a-t-il quelque chose de plus proche de la réalité?

Bien sûr! Nous avons déjà dit à plusieurs reprises que la collecte de statistiques (c'est-à-dire le calcul de matrices de corrélation et de vecteurs) dans des systèmes en temps réel est loin d'être toujours un luxe abordable. Cependant, l'humanité s'est adaptée à ces difficultés: au lieu d'une approche déterministe dans la pratique, des approches adaptatives sont utilisées. Ils peuvent être divisés en deux grands groupes [1, p. 246]:

probabiliste (stochastique) (par exemple SG - Gradient stochastique)
et basé sur la méthode des moindres carrés (par exemple, LMS - Least Mean Squares ou RLS - Recursive Least Squares)

Le sujet des filtres adaptatifs est bien représenté au sein de la communauté open-source (exemples pour python):

Dans le deuxième exemple, j'aime particulièrement la documentation. Attention cependant! Lorsque j'ai testé le paquet padasip , j'ai rencontré des difficultés dans la gestion des nombres complexes (par défaut, float64 y est impliqué). Peut-être que les mêmes problèmes peuvent survenir lorsque vous travaillez avec d'autres implémentations.

Bien entendu, les algorithmes ont leurs propres avantages et inconvénients, dont la somme détermine la portée de l'algorithme.

Jetons un coup d'œil aux exemples: nous allons considérer les trois algorithmes SG , LMS et RLS que nous avons déjà mentionnés (nous modéliserons en langage MATLAB - j'avoue, il y avait déjà des blancs, et tout réécrire en uniformité python pour le bien de ... eh bien ...).

Une description des algorithmes LMS et RLS peut être trouvée, par exemple, dans le dock padasip .

La description de SG peut être trouvée ici.

La principale différence avec la descente du gradient est un gradient variable:

$\ mathbf {w} [n] = \ mathbf {w} [n-1] + \ mu \ left (\ mathbf {\ hat {p}} [n] - \ mathbf {\ hat {R}} _ {xx } [n] \ mathbf {w} [n-1] \ droite)$

$\ mathbf {\ hat {R}} _ {xx} [n] = \ frac {1} {n} \ left ((n-1) \ mathbf {\ hat {R}} _ {xx} [n-1 ] + \ mathbf {x} [n] \ mathbf {x} [n] ^ H \ droite)$

$\ mathbf {\ hat {p}} [n] = \ frac {1} {n} \ left ((n-1) \ mathbf {\ hat {p}} [n-1] + \ mathbf {x} [ n] d [n] ^ * \ droite)$

1) Un cas similaire à celui considéré ci-dessus.

Sources (MatLab / Octave).

Les sources peuvent être téléchargées ici .

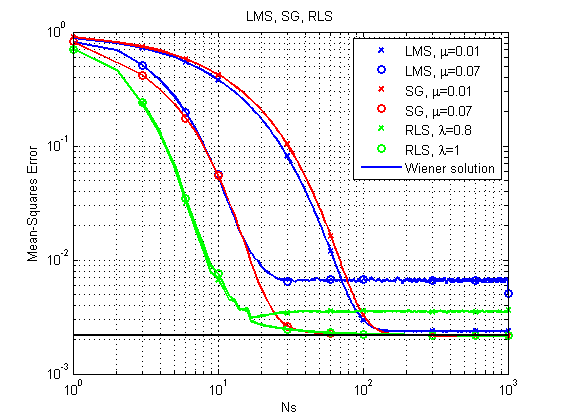
Fig. 6. Courbes d'apprentissage pour LMS, RLS et SG.

On peut immédiatement noter qu'avec sa relative simplicité, l'algorithme LMS peut, en principe, ne pas aboutir à une solution optimale avec un pas relativement important. RLS donne le résultat le plus rapide, mais il peut également échouer avec un facteur d'oubli relativement faible. Jusqu'à présent, SG se porte bien, mais regardons un autre exemple.

2) Le cas où le canal change dans le temps.

Sources (MatLab / Octave).

Les sources peuvent être téléchargées ici .

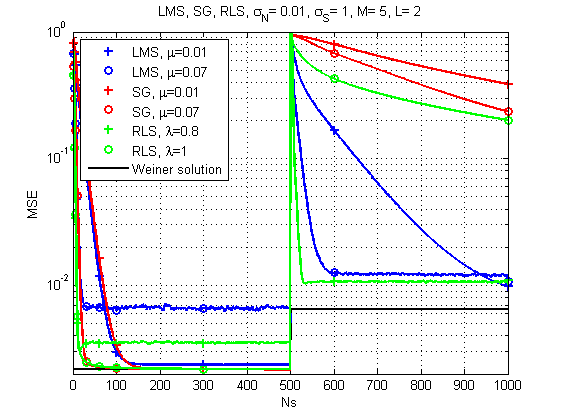
Fig. 7. Courbes d'apprentissage pour LMS, RLS et SG (changements de canaux dans le temps).

Et ici, l'image est déjà beaucoup plus intéressante: avec un fort changement dans la réponse du canal, le LMS semble déjà être la solution la plus fiable. Qui aurait pensé. Bien que RLS avec le bon facteur d'oubli fournisse également un résultat acceptable.

Quelques mots sur la performance.

Oui, bien sûr, chaque algorithme a sa propre complexité de calcul, mais selon mes mesures, mon ancienne machine peut faire face à un ensemble pour environ 120 μs par itération dans le cas de LMS et SG et environ 250 μs par itération dans le cas de RLS. Autrement dit, la différence est, en général, comparable.

Et c'est tout pour aujourd'hui. Merci à tous ceux qui ont regardé!

Littérature

Théorie du filtre adaptatif Haykin SS. - Pearson Education India, 2005.
Haykin, Simon et KJ Ray Liu. Manuel sur le traitement des réseaux et les réseaux de capteurs. Vol. 63. John Wiley & Sons, 2010. pp. 102-107
Arndt, D. (2015). Modélisation On Channel pour la réception satellite terrestre mobile (thèse de doctorat).

Annexe 1

Filtre propre

L'objectif principal d'un tel filtre est de maximiser le rapport signal / bruit (SNR).

Mais à en juger par la présence de corrélations dans les calculs, il s'agit aussi davantage d'une construction théorique que d'une solution pratique.

Filtrage linéaire optimal: de la descente de gradient aux filtres adaptatifs