En 1998, Lawrence Page, Sergey Brin, Rajiv Motwani et Terry Vinograd ont publié l'article «The PageRank Citation Ranking: Bringing Order to the Web», qui décrivait le désormais célèbre algorithme PageRank, qui est devenu le fondement de Google. Après un peu moins de deux décennies, Google est devenu un géant, et même si son algorithme a beaucoup évolué, le PageRank est toujours le «symbole» des algorithmes de classement de Google (bien que seules quelques personnes puissent vraiment dire combien de poids il prend dans l'algorithme aujourd'hui) .
D'un point de vue théorique, il est intéressant de noter que l'une des interprétations standard de l'algorithme PageRank est basée sur un concept simple mais fondamental des chaînes de Markov. À partir de l'article, nous verrons que les chaînes de Markov sont de puissants outils de modélisation stochastique qui peuvent être utiles à tout scientifique des données. En particulier, nous répondrons à ces questions fondamentales: quelles sont les chaînes de Markov, quelles bonnes propriétés possèdent-elles et que peut-on faire avec leur aide?
Brève revue
Dans la première section, nous donnons les définitions de base nécessaires à la compréhension des chaînes de Markov. Dans la deuxième section, nous considérons le cas particulier des chaînes de Markov dans un espace à états finis. Dans la troisième section, nous considérons certaines des propriétés élémentaires des chaînes de Markov et illustrons ces propriétés avec de nombreux petits exemples. Enfin, dans la quatrième section, nous associons les chaînes de Markov à l'algorithme PageRank et voyons avec un exemple artificiel comment les chaînes de Markov peuvent être utilisées pour classer les nœuds d'un graphique.
Remarque La compréhension de ce poste nécessite une connaissance des bases de la probabilité et de l'algèbre linéaire. En particulier, les concepts suivants seront utilisés: probabilité conditionnelle , vecteur propre et formule de probabilité complète .
Quelles sont les chaînes de Markov?
Variables aléatoires et processus aléatoires
Avant d'introduire le concept de chaînes de Markov, rappelons brièvement les concepts fondamentaux mais importants de la théorie des probabilités.
Premièrement, en dehors du langage des mathématiques, une
variable aléatoire X est une quantité qui est déterminée par le résultat d'un phénomène aléatoire. Son résultat peut être un nombre (ou "similitude d'un nombre", par exemple, des vecteurs) ou autre chose. Par exemple, nous pouvons définir une variable aléatoire comme le résultat d'un jet de dé (nombre) ou comme le résultat d'un tirage au sort (pas un nombre, sauf si nous désignons, par exemple, "aigle" comme 0, mais "queues" comme 1). Nous mentionnons également que l'espace des résultats possibles d'une variable aléatoire peut être discret ou continu: par exemple, une variable aléatoire normale est continue, et une variable aléatoire de Poisson est discrète.
De plus, nous pouvons définir un
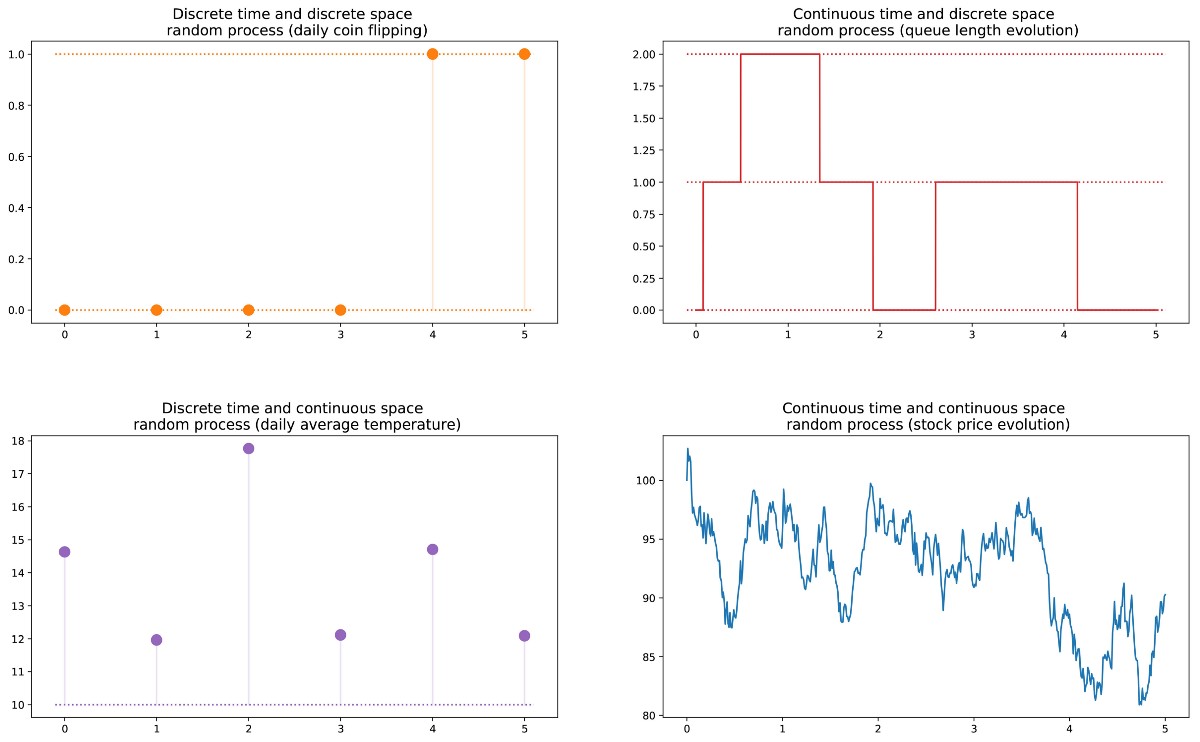
processus aléatoire (également appelé stochastique) comme un ensemble de variables aléatoires indexées par l'ensemble T, qui dénote souvent différents moments dans le temps (dans ce qui suit, nous supposerons cela). Les deux cas les plus courants: T peut être soit un ensemble de nombres naturels (processus aléatoire à temps discret), soit un ensemble de nombres réels (processus aléatoire à temps continu). Par exemple, si nous jetons une pièce tous les jours, nous définirons un processus aléatoire avec une heure discrète, et la valeur toujours changeante d'une option sur l'échange définira un processus aléatoire avec une heure continue. Les variables aléatoires à différents moments peuvent être indépendantes les unes des autres (un exemple avec un tirage au sort), ou avoir une sorte de dépendance (un exemple avec la valeur de l'option); de plus, ils peuvent avoir un espace d'état continu ou discret (l'espace des résultats possibles à chaque instant).
Propriété Markov et chaîne Markov
Il existe des familles bien connues de processus aléatoires: processus gaussiens, processus de Poisson, modèles autorégressifs, modèles à moyenne mobile, chaînes de Markov et autres. Chacun de ces cas individuels possède certaines propriétés qui nous permettent de mieux les explorer et les comprendre.
L'une des propriétés qui simplifie considérablement l'étude d'un processus aléatoire est la propriété Markov. Si nous l'expliquons dans un langage très informel, la propriété Markov nous dit que si nous connaissons la valeur obtenue par un processus aléatoire à un moment donné, nous ne recevrons aucune information supplémentaire sur le comportement futur du processus, en collectant d'autres informations sur son passé. Dans un langage plus mathématique: à tout moment, la distribution conditionnelle des états futurs d'un processus avec des états actuels et passés donnés ne dépend que de l'état actuel, et non des états passés (la
propriété du manque de mémoire ). Un processus aléatoire avec une propriété Markov est appelé
processus Markov .
La propriété Markov signifie que si nous connaissons l'état actuel à un moment donné, nous n'avons pas besoin d'informations supplémentaires sur l'avenir, collectées sur le passé.Sur la base de cette définition, nous pouvons formuler la définition de «chaînes de Markov homogènes à temps discret» (ci-après pour des raisons de simplicité, nous les appellerons «chaînes de Markov»).
La chaîne de Markov est un processus de Markov avec un temps discret et un espace d'état discret. Ainsi, une chaîne de Markov est une séquence d'états discrets, dont chacun est extrait d'un espace d'états discrets (fini ou infini), satisfaisant la propriété de Markov.
Mathématiquement, nous pouvons désigner la chaîne de Markov comme suit:
où à chaque instant le processus prend ses valeurs dans un ensemble discret E, tel que
Ensuite, la propriété Markov implique que nous avons
Notez à nouveau que cette dernière formule reflète le fait que pour la chronologie (où je suis maintenant et où j'étais auparavant) la distribution de probabilité de l'état suivant (où je serai le prochain) dépend de l'état actuel, mais pas des états passés.
Remarque Dans ce billet introductif, nous avons décidé de ne parler que de simples chaînes de Markov homogènes à temps discret. Cependant, il existe également des chaînes de Markov inhomogènes (dépendantes du temps) et / ou des chaînes à temps continu. Dans cet article, nous ne considérerons pas de telles variations du modèle. Il convient également de noter que la définition ci-dessus d'une propriété de Markov est extrêmement simplifiée: la véritable définition mathématique utilise le concept de filtrage, qui va bien au-delà de notre connaissance introductive du modèle.
Nous caractérisons la dynamique d'aléatoire d'une chaîne de Markov
Dans la sous-section précédente, nous nous sommes familiarisés avec la structure générale correspondant à toute chaîne de Markov. Voyons ce dont nous avons besoin pour définir une "instance" spécifique d'un tel processus aléatoire.
Tout d'abord, nous notons que la détermination complète des caractéristiques d'un processus aléatoire à temps discret qui ne satisfait pas la propriété de Markov peut être difficile: la distribution de probabilité à un moment donné peut dépendre d'un ou de plusieurs moments du passé et / ou du futur. Toutes ces dépendances temporelles possibles peuvent potentiellement compliquer la création d'une définition de processus.
Cependant, en raison de la propriété Markov, la dynamique de la chaîne de Markov est assez simple à déterminer. Et en effet. nous devons déterminer seulement deux aspects: la
distribution de probabilité initiale (c'est-à-dire la distribution de probabilité au temps n = 0), notée par
et
la matrice de probabilité de transition (qui nous donne les probabilités que l'état au temps n + 1 soit le suivant pour un autre état au temps n pour n'importe quelle paire d'états), noté par
Si ces deux aspects sont connus, alors la dynamique complète (probabiliste) du processus est clairement définie. Et en fait, la probabilité de tout résultat du processus peut alors être calculée de manière cyclique.
Exemple: supposons que nous voulons connaître la probabilité que les 3 premiers états du processus aient des valeurs (s0, s1, s2). Autrement dit, nous voulons calculer la probabilité
Ici, nous appliquons la formule de la probabilité totale, qui stipule que la probabilité d'obtenir (s0, s1, s2) est égale à la probabilité d'obtenir les premiers s0 fois la probabilité d'obtenir s1, étant donné que nous avons précédemment obtenu s0 fois la probabilité d'obtenir s2 en tenant compte du fait que nous avons obtenu plus tôt dans l'ordre s0 et s1. Mathématiquement, cela peut être écrit comme
Et puis la simplification est révélée, déterminée par l'hypothèse de Markov. Et en fait, dans le cas des chaînes longues, on obtient des probabilités fortement conditionnelles pour ces derniers états. Cependant, dans le cas des chaînes de Markov, nous pouvons simplifier cette expression en profitant du fait que
obtenir de cette façon
Puisqu'ils caractérisent pleinement la dynamique probabiliste du processus, de nombreux événements complexes ne peuvent être calculés que sur la base de la distribution de probabilité initiale q0 et de la matrice de probabilité de transition p. Il convient également de mentionner un autre lien de base: l'expression de la distribution de probabilité au temps n + 1, exprimée par rapport à la distribution de probabilité au temps n
Chaînes de Markov dans les espaces d'états finis
Représentation matricielle et graphique
Ici, nous supposons que l'ensemble E a un nombre fini d'états possibles N:
Ensuite, la distribution de probabilité initiale peut être décrite comme
un vecteur ligne q0 de taille N, et les probabilités de transition peuvent être décrites comme une matrice p de taille N par N, de telle sorte que
L'avantage de cette notation est que si nous notons la distribution de probabilité à l'étape n par le vecteur ligne qn tel que ses composantes sont spécifiées
alors les relations matricielles simples sont préservées
(ici nous ne considérerons pas la preuve, mais il est très simple de la reproduire).
Si nous multiplions le vecteur ligne à droite, qui décrit la distribution de probabilité à un moment donné, par la matrice de probabilité de transition, alors nous obtenons la distribution de probabilité au stade suivant.Ainsi, comme nous le voyons, la transition de la distribution de probabilité d'un stade donné au suivant est simplement définie comme la multiplication correcte du vecteur ligne de probabilités de l'étape initiale par la matrice p. De plus, cela implique que nous avons
La dynamique aléatoire d'une chaîne de Markov dans un espace d'états finis peut facilement être représentée comme un graphe orienté normalisé de telle sorte que chaque nœud du graphe est un état, et pour chaque paire d'états (ei, ej) il existe un bord allant de ei à ej si p (ei, ej )> 0. La valeur de bord sera alors la même probabilité p (ei, ej).
Exemple: un lecteur de notre site
Illustrons tout cela avec un exemple simple. Considérez le comportement quotidien d'un visiteur fictif sur un site. Chaque jour, il a 3 conditions possibles: le lecteur ne visite pas le site ce jour-là (N), le lecteur visite le site, mais ne lit pas l'intégralité du post (V), et le lecteur visite le site et lit un post entier (R). Nous avons donc l'espace d'état suivant:
Supposons que le premier jour, ce lecteur ait 50% de chances d'accéder uniquement au site et 50% de chances de visiter le site et de lire au moins un article. Le vecteur décrivant la distribution de probabilité initiale (n = 0) ressemble alors à ceci:
Imaginez également que les probabilités suivantes sont observées:
- lorsque le lecteur ne visite pas un jour, il y a une probabilité de 25% de ne pas lui rendre visite le lendemain, une probabilité de 50% seulement de lui rendre visite et de 25% de visiter et de lire l'article
- lorsque le lecteur visite le site un jour, mais ne lit pas, il a 50% de chances de le visiter à nouveau le lendemain sans lire l'article, et 50% de chances de visiter et de lire
- lorsqu'un lecteur visite et lit un article le même jour, il a 33% de chances de ne pas se connecter le lendemain (j'espère que ce message n'aura pas un tel effet!) , 33% de chances de se connecter uniquement au site et 34% de visiter et de relire l'article
Ensuite, nous avons la matrice de transition suivante:
De la sous-section précédente, nous savons comment calculer pour ce lecteur la probabilité de chaque état le lendemain (n = 1)
La dynamique probabiliste de cette chaîne de Markov peut être représentée graphiquement comme suit:
Présentation sous forme de graphique de la chaîne de Markov, modélisant le comportement de notre visiteur inventé sur le site.Propriétés des chaînes de Markov
Dans cette section, nous ne parlerons que de certaines des propriétés ou caractéristiques les plus fondamentales des chaînes de Markov. Nous n'entrerons pas dans les détails mathématiques, mais fournirons un bref aperçu des points intéressants qui doivent être étudiés pour utiliser les chaînes de Markov. Comme nous l'avons vu, dans le cas d'un espace à états finis, la chaîne de Markov peut être représentée sous forme de graphe. À l'avenir, nous utiliserons la représentation graphique pour expliquer certaines propriétés. Cependant, n'oubliez pas que ces propriétés ne sont pas nécessairement limitées au cas d'un espace d'états fini.
Décomposabilité, périodicité, irrévocabilité et récupérabilité
Dans cette sous-section, commençons par plusieurs façons classiques de caractériser un état ou une chaîne de Markov entière.
Tout d'abord, nous mentionnons que la chaîne de Markov est
indécomposable s'il est possible d'atteindre n'importe quel état à partir de n'importe quel autre état (ce n'est pas nécessaire qu'en une seule étape de temps). Si l'espace d'état est fini et que la chaîne peut être représentée sous forme de graphe, alors nous pouvons dire que le graphe d'une chaîne de Markov indécomposable est fortement connecté (théorie des graphes).
Illustration de la propriété de l'indécomposabilité (irréductibilité). La chaîne de gauche ne peut pas être raccourcie: à partir de 3 ou 4, nous ne pouvons pas entrer dans 1 ou 2. La chaîne de droite (un bord est ajouté) peut être raccourcie: chaque état peut être atteint à partir de n'importe quel autre.Un état a une période k si, à sa sortie, pour tout retour à cet état, le nombre de pas de temps est un multiple de k (k est le plus grand diviseur commun de toutes les longueurs possibles de chemins de retour). Si k = 1, alors ils disent que l'état est apériodique, et toute la chaîne de Markov est
apériodique si tous ses états sont apériodiques. Dans le cas d'une chaîne de Markov irréductible, on peut également mentionner que si un état est apériodique, alors tous les autres sont également apériodiques.
Illustration de la propriété de périodicité. La chaîne de gauche est périodique avec k = 2: lorsque vous quittez un état, y revenir nécessite toujours le nombre de pas multiple de 2. La chaîne de droite a une période de 3.Un état est
irrévocable si, à sa sortie, il y a une probabilité non nulle que nous n'y revenions jamais. Inversement, un état est considéré comme
retournable si nous savons qu'après avoir quitté l'état, nous pouvons y revenir à l'avenir avec la probabilité 1 (s'il n'est pas irrévocable).
Illustration de la propriété de retour / irrévocabilité. La chaîne de gauche a les propriétés suivantes: 1, 2 et 3 sont irrévocables (en quittant ces points, nous ne pouvons pas être absolument sûrs que nous y reviendrons) et ont une période de 3, et 4 et 5 sont retournables (en quittant ces points, nous sommes absolument sûrs un jour, nous y reviendrons) et avons une période de 2. La chaîne de droite a une autre nervure, ce qui rend la chaîne entière retournable et apériodique.Pour l'état de retour, nous pouvons calculer le temps de retour moyen, qui est le
temps de retour attendu en quittant l'état. Notez que même la probabilité d'un retour est 1, cela ne signifie pas que le temps de retour attendu est fini. Par conséquent, parmi tous les états de retour, nous pouvons distinguer
les états de retour positifs (avec un temps de retour attendu fini) et les
états de retour zéro (avec un temps de retour attendu infini).
Distribution stationnaire, comportement marginal et ergodicité
Dans cette sous-section, nous considérons les propriétés qui caractérisent certains aspects de la dynamique (aléatoire) décrite par la chaîne de Markov.
La distribution de probabilité π sur l'espace d'état E est appelée
distribution stationnaire si elle satisfait l'expression
Puisque nous avons
Alors la distribution stationnaire satisfait l'expression
Par définition, la distribution de probabilité stationnaire ne change pas avec le temps. Autrement dit, si la distribution initiale q est stationnaire, elle sera la même à toutes les étapes ultérieures du temps. Si l'espace d'état est fini, alors p peut être représenté comme une matrice, et π comme un vecteur ligne, puis nous obtenons
Cela exprime à nouveau le fait que la distribution de probabilité stationnaire ne change pas avec le temps (comme nous le voyons, multiplier la distribution de probabilité à droite par p nous permet de calculer la distribution de probabilité à l'étape suivante du temps). Gardez à l'esprit qu'une chaîne de Markov indécomposable a une distribution de probabilité stationnaire si et seulement si l'un de ses états est un retour positif.
Une autre propriété intéressante liée à la distribution de probabilité stationnaire est la suivante. Si la chaîne est un retour positif (c'est-à-dire qu'il y a une distribution stationnaire) et apériodique, alors, quelles que soient les probabilités initiales, la distribution de probabilité de la chaîne converge alors que les intervalles de temps tendent vers l'infini: ils disent que la chaîne a une
distribution limite , qui n'est rien d'autre, comme une distribution stationnaire. En général, cela peut être écrit comme ceci:
Nous soulignons une fois de plus que nous ne faisons aucune hypothèse sur la distribution de probabilité initiale: la distribution de probabilité de la chaîne se réduit à une distribution stationnaire (distribution d'équilibre de la chaîne) quels que soient les paramètres initiaux.Enfin, l' ergodicité est une autre propriété intéressante liée au comportement de la chaîne de Markov. Si la chaîne de Markov est indécomposable, alors on dit aussi qu'elle est «ergodique» car elle satisfait au théorème ergodique suivant. Supposons que nous ayons une fonction f (.) Qui va de l'espace d'état E à l'axe (cela peut être, par exemple, le prix d'être dans chaque état). Nous pouvons déterminer la valeur moyenne qui déplace cette fonction le long d'une trajectoire donnée (moyenne temporelle). Pour les nèmes premiers termes, cela est noté commeOn peut également calculer la valeur moyenne de la fonction f sur l'ensemble E, pondérée par la distribution stationnaire (moyenne spatiale), qui est notéeLe théorème ergodique nous dit alors que lorsque la trajectoire devient infiniment longue, la moyenne temporelle est égale à la moyenne spatiale (pondérée par la distribution stationnaire). La propriété ergodicity peut s'écrire comme suit:En d'autres termes, cela signifie que dans la limite antérieure, le comportement de la trajectoire devient insignifiant et seul le comportement stationnaire à long terme est important lors du calcul de la moyenne temporelle.Revenons à l'exemple avec le lecteur de site
Encore une fois, considérons l'exemple du lecteur de site. Dans cet exemple simple, il est évident que la chaîne est indécomposable, apériodique et que tous ses états sont positivement retournables.Pour montrer quels résultats intéressants peuvent être calculés à l'aide des chaînes de Markov, nous considérons le temps moyen de retour à l'état R (l'état «visite le site et lit l'article»). En d'autres termes, nous voulons répondre à la question suivante: si notre lecteur visite un jour le site et lit un article, alors combien de jours devra-t-il attendre en moyenne pour qu'il revienne lire l'article? Essayons d'obtenir un concept intuitif de la façon dont cette valeur est calculée.On note d'abordNous voulons donc calculer m (R, R). En parlant du premier intervalle atteint après avoir quitté R, on obtientCependant, cette expression nécessite que pour le calcul de m (R, R) nous connaissions m (N, R) et m (V, R). Ces deux quantités peuvent être exprimées de manière similaire:Ainsi, nous avons obtenu 3 équations avec 3 inconnues et après les avoir résolues, nous obtenons m (N, R) = 2,67, m (V, R) = 2,00 et m (R, R) = 2,54. Le temps moyen pour revenir à l'état R est alors de 2,54. Autrement dit, en utilisant l'algèbre linéaire, nous avons pu calculer le temps moyen de retour à l'état R (ainsi que le temps de transition moyen de N à R et le temps de transition moyen de V à R).Pour terminer avec cet exemple, voyons quelle sera la distribution stationnaire de la chaîne de Markov. Pour déterminer la distribution stationnaire, nous devons résoudre l'équation d'algèbre linéaire suivante:Autrement dit, nous devons trouver le vecteur propre gauche p associé au vecteur propre 1. En résolvant ce problème, nous obtenons la distribution stationnaire suivante:Distribution stationnaire dans l'exemple avec le lecteur de site.Vous pouvez également remarquer que π (R) = 1 / m (R, R), et si un peu de réflexion, alors cette identité est tout à fait logique (mais nous n'en parlerons pas en détail).La chaîne étant indécomposable et apériodique, cela signifie qu'à long terme la distribution de probabilité converge vers une distribution stationnaire (pour tous les paramètres initiaux). En d'autres termes, quel que soit l'état initial du lecteur du site, si nous attendons assez longtemps et sélectionnons un jour au hasard, nous aurons la probabilité π (N) que le lecteur ne visitera pas le site ce jour-là, la probabilité π (V) que le lecteur s'arrêtera mais ne lira pas l'article, et la probabilité est π® que le lecteur s'arrête et lise l'article. Pour mieux comprendre la propriété de la convergence, regardons le graphique suivant montrant l'évolution des distributions de probabilité à partir de différents points de départ et convergeant (rapidement) vers une distribution stationnaire:Visualisation de la convergence de 3 distributions de probabilité avec différents paramètres initiaux (bleu, orange et vert) vers la distribution stationnaire (rouge).Exemple classique: algorithme de PageRank
Il est temps de revenir au PageRank! Mais avant de poursuivre, il convient de mentionner que l'interprétation du PageRank donnée dans cet article n'est pas la seule possible, et les auteurs de l'article d'origine ne se sont pas nécessairement appuyés sur l'utilisation de chaînes de Markov pour développer la méthodologie. Cependant, notre interprétation est bonne car elle est très claire.Utilisateur Web arbitraire
PageRank essaie de résoudre le problème suivant: comment pouvons-nous classer un ensemble existant (nous pouvons supposer que cet ensemble a déjà été filtré, par exemple, par une requête) en utilisant des liens déjà existants entre les pages?Pour résoudre ce problème et pouvoir classer les pages, PageRank effectue approximativement le processus suivant. Nous pensons qu'un internaute arbitraire à la première fois est sur l'une des pages. Ensuite, cet utilisateur commence à se déplacer au hasard, en cliquant sur chaque page sur l'un des liens qui mènent à une autre page de l'ensemble en question (il est supposé que tous les liens menant en dehors de ces pages sont interdits). Sur n'importe quelle page, tous les liens valides ont la même probabilité de cliquer.C'est ainsi que nous définissons la chaîne de Markov: les pages sont des états possibles, les probabilités de transition sont définies par des liens de page en page (pondérés de telle sorte que sur chaque page toutes les pages liées ont la même probabilité de sélection), et les propriétés du manque de mémoire sont clairement déterminées par le comportement de l'utilisateur. Si nous supposons également que la chaîne donnée est retournable positivement et apériodique (de petites astuces sont utilisées pour satisfaire ces exigences), alors à long terme, la distribution de probabilité de la «page actuelle» converge vers une distribution stationnaire. Autrement dit, quelle que soit la page initiale, après une longue période, chaque page a une probabilité (presque fixe) de devenir actuelle si nous choisissons un moment aléatoire dans le temps.Le PageRank est basé sur l'hypothèse suivante: les pages les plus probables d'une distribution stationnaire devraient également être les plus importantes (nous visitons souvent ces pages parce qu'elles obtiennent des liens de pages qui sont également fréquemment visitées pendant les transitions). Ensuite, la distribution de probabilité stationnaire détermine la valeur du PageRank pour chaque état.Exemple artificiel
Pour rendre cela beaucoup plus clair, regardons un exemple artificiel. Supposons que nous ayons un petit site Web de 7 pages, libellé de 1 à 7, et que les liens entre ces pages correspondent à la colonne suivante.Par souci de clarté, les probabilités de chaque transition dans l'animation ci-dessus ne sont pas affichées. Cependant, comme on suppose que la «navigation» doit être exclusivement aléatoire (c'est ce qu'on appelle «marche aléatoire»), les valeurs peuvent être facilement reproduites à partir de la règle simple suivante: pour un site avec K liens sortants (page avec K liens vers d'autres pages), la probabilité de chaque lien sortant égal à 1 / K. Autrement dit, la matrice de probabilité de transition a la forme:où les valeurs de 0,0 sont remplacées par commodité par ".". Avant d'effectuer d'autres calculs, nous pouvons remarquer que cette chaîne de Markov est indécomposable et apériodique, c'est-à-dire qu'à long terme le système converge vers une distribution stationnaire. Comme nous l'avons vu, cette distribution stationnaire peut être calculée en résolvant le problème de vecteur propre gauche suivantCe faisant, nous obtenons les valeurs de PageRank suivantes (valeurs de distribution stationnaires) pour chaque pageValeurs de PageRank calculées pour notre exemple artificiel de 7 pages.Ensuite, le classement PageRank de ce petit site Web est 1> 7> 4> 2> 5 = 6> 3.
Conclusions
Principales conclusions de cet article:- les processus aléatoires sont des ensembles de variables aléatoires qui sont souvent indexées par le temps (les indices indiquent souvent un temps discret ou continu)
- pour un processus aléatoire, la propriété de Markov signifie que pour un courant donné, la probabilité de l'avenir ne dépend pas du passé (cette propriété est aussi appelée «manque de mémoire»)
- chaîne de Markov à temps discret est des processus aléatoires avec des indices à temps discret satisfaisant la propriété de Markov
- ( , …)
- PageRank ( ) -, ; ( , , , )
, , . , , ( , , ), ( - ), ( ), ( ), .
Bien sûr, les énormes opportunités offertes par les chaînes de Markov du point de vue de la modélisation et du calcul sont beaucoup plus larges que celles considérées dans cette modeste revue. Par conséquent, nous espérons avoir pu susciter l'intérêt du lecteur à poursuivre l'étude de ces outils, qui occupent une place importante dans l'arsenal d'un scientifique et expert en données.