Ce n'est un secret pour personne que l'un des passe-temps préférés d'un développeur de logiciels est d'interviewer des employeurs. Nous le faisons tous de temps en temps et pour des raisons complètement différentes. Et la plus évidente d'entre elles - la recherche d'emploi - n'est pas, je pense, la plus courante. Assister à un entretien est un bon moyen de rester en forme, de répéter les bases oubliées et d'apprendre quelque chose de nouveau. Et en cas de succès, augmentez également la confiance en soi. Nous nous ennuyons, nous nous fixons le statut «ouvert aux offres» dans une sorte de réseau social «professionnel» comme
«LinkedIn» - et l'armée de gestionnaires des ressources humaines attaque déjà nos boîtes de réception pour les messages entrants.

Dans le processus, alors que tout ce débat se déroule, nous sommes confrontés à de nombreuses questions qui, comme ils le disent de l'autre côté du rideau implicitement effondré, «sonnent la cloche» et leurs détails sont cachés derrière le
brouillard de la guerre . Ils ne sont le plus souvent rappelés que dans des tests par des algorithmes et des structures de données (personnellement, je n'avais pas de telles données du tout) et en fait des entretiens.
L'une des questions les plus courantes dans une interview pour un programmeur de toute spécialisation est les listes. Par exemple, des listes liées individuellement. Et les algorithmes de base associés. Par exemple, un demi-tour. Et généralement, cela se produit en quelque sorte comme ceci: "Bien, mais comment développeriez-vous une liste liée individuellement?" L'essentiel est de surprendre le demandeur par cette question.
En fait, tout cela m'a amené à écrire cette courte critique pour rappel constant et édification. Alors, blague à part, voici!
Liste liée individuellement
Une liste chaînée est l'une des
structures de données de base. Chaque élément (ou nœud) de celui-ci se compose en fait de données stockées et de liens vers des éléments voisins. Une liste liée individuellement stocke uniquement le lien vers l'élément suivant dans la structure, et une liste
doublement liée contient le suivant et le précédent. Une telle organisation des données permet de les localiser dans n'importe quelle zone mémoire (contrairement, par exemple, à un
tableau dont tous les éléments doivent être localisés en mémoire les uns après les autres).
Il y a bien sûr beaucoup plus à dire sur les listes: elles peuvent être circulaires (c'est-à-dire que le dernier élément stocke un lien vers le premier) ou non (c'est-à-dire qu'il n'y a pas de lien vers le dernier élément). Les listes peuvent être saisies, c.-à-d. contiennent des données du même type ou non. Et ainsi de suite et ainsi de suite.
Mieux vaut essayer d'écrire du code. Par exemple, vous pouvez en quelque sorte imaginer un nœud de liste:
final class Node<T> { let payload: T var nextNode: Node? init(payload: T, nextNode: Node? = nil) { self.payload = payload self.nextNode = nextNode } }
«Générique» est un type capable de stocker des charges utiles de tout type dans le champ de
payload .
La liste elle-même est exhaustivement identifiée par son premier nœud:
final class SinglyLinkedList<T> { var firstNode: Node<T>? init(firstNode: Node<T>? = nil) { self.firstNode = firstNode } }
Le premier nœud est déclaré facultatif, car la liste peut très bien être vide.
En théorie, bien sûr, dans la classe, vous devez implémenter toutes les méthodes nécessaires - insérer, supprimer, accéder aux nœuds, etc., mais nous le ferons une autre fois. Dans le même temps, nous vérifierons si l'utilisation de struct (avec laquelle Apple nous encourage activement par notre exemple) est un meilleur choix, et nous rappellerons peut-être l'approche «Copier sur écriture» .Propagation de liste à lien unique
La première façon. Cycle
Il est temps de passer aux affaires pour lesquelles nous sommes ici aujourd'hui! Et le moyen le plus efficace pour y faire face est de deux manières. Le premier est une simple boucle, du premier au dernier nœud.
Le cycle fonctionne avec trois variables qui, avant le début, se voient attribuer la valeur du nœud précédent, actuel et suivant. (À ce moment, la valeur du nœud précédent est naturellement vide.) Le cycle commence par vérifier que le nœud suivant n'est pas vide, et si c'est le cas, le corps du cycle est exécuté. Aucune magie ne se produit dans la boucle: au nœud actuel, le champ qui fait référence à l'élément suivant se voit attribuer un lien vers le précédent (à la première itération, la valeur du lien, respectivement, est réinitialisée, ce qui correspond à la situation dans le dernier nœud). Eh bien et plus loin, les variables correspondant aux nœuds précédent, actuel et suivant reçoivent de nouvelles valeurs. Après avoir quitté la boucle, le nœud actuel (c'est-à-dire le dernier itérable en général) se voit attribuer une nouvelle valeur de lien vers le nœud suivant, car la sortie de la boucle se produit juste au moment où le dernier nœud de la liste devient courant.
En mots, bien sûr, tout cela semble étrange et incompréhensible, il est donc préférable de regarder le code:
extension SinglyLinkedList { func reverse() { var previousNode: Node<T>? = nil var currentNode = firstNode var nextNode = firstNode?.nextNode while nextNode != nil { currentNode?.nextNode = previousNode previousNode = currentNode currentNode = nextNode nextNode = currentNode?.nextNode } currentNode?.nextNode = previousNode firstNode = currentNode } }
Pour la vérification, nous utilisons une liste de nœuds dont les charges utiles sont de simples identifiants
entiers . Créez une liste de dix éléments:
let node = Node(payload: 0)
Tout semble aller bien, mais nous sommes des personnes, pas des ordinateurs, et il serait bien pour nous d'obtenir une preuve visuelle de l'exactitude de la liste créée et de l'algorithme décrit ci-dessus. Peut-être qu'une simple impression suffira. Pour rendre la sortie lisible, ajoutez l'implémentation du protocole
CustomStringConvertible nœud avec un identifiant entier:
extension Node: CustomStringConvertible where T == Int { var description: String { let firstPart = """ Node \(Unmanaged.passUnretained(self).toOpaque()) has id \(payload) and """ if let nextNode = nextNode { return firstPart + " next node \(nextNode.payload)." } else { return firstPart + " no next node." } } }
... Et la liste correspondante pour afficher tous les nœuds dans l'ordre:
extension SinglyLinkedList: CustomStringConvertible where T == Int { var description: String { var description = """ List \(Unmanaged.passUnretained(self).toOpaque()) """ if firstNode != nil { description += " has nodes:\n" var node = firstNode while node != nil { description += (node!.description + "\n") node = node!.nextNode } return description } else { return description + " has no nodes." } } }
La représentation sous forme de chaîne de nos types contiendra une adresse en mémoire et un identifiant entier. A partir de ceux-ci, nous organisons l'impression de la liste générée de dix nœuds:
print(String(describing: list))
Développez cette liste et imprimez-la à nouveau:
list.reverse() print(String(describing: list))
Vous pouvez remarquer que les adresses dans la mémoire de la liste et des nœuds n'ont pas changé et que les nœuds de la liste sont imprimés dans l'ordre inverse. Les références à l'élément suivant du nœud pointent maintenant vers le précédent (c'est-à-dire, par exemple, que l'élément suivant du nœud "5" n'est plus "6", mais "4"). Et cela signifie que nous l'avons fait!
La deuxième façon. Récursivité
La deuxième façon connue de faire le même demi-tour est basée sur la
récursivité . Pour l'implémenter, nous allons déclarer une fonction qui prend le premier noeud de la liste, et retourne le «nouveau» premier noeud (qui était le dernier avant).
Le paramètre et la valeur de retour sont facultatifs, car à l'intérieur de cette fonction, elle est appelée à plusieurs reprises sur chaque nœud suivant jusqu'à ce qu'elle soit vide (c'est-à-dire jusqu'à ce que la fin de la liste soit atteinte). En conséquence, dans le corps de la fonction, il est nécessaire de vérifier si le noeud sur lequel la fonction est appelée est vide et si ce noeud possède les éléments suivants. Sinon, la fonction renvoie ce qui a été passé à l'argument.
En fait, j'ai honnêtement essayé de décrire l'algorithme complet avec des mots, mais au final j'ai effacé presque tout, car le résultat serait impossible à comprendre. Pour dessiner des organigrammes et décrire officiellement les étapes de l'algorithme - aussi, dans ce cas, je pense que cela n'a aucun sens, car il sera plus pratique pour vous et moi de simplement lire et essayer de comprendre le code
Swift :
extension SinglyLinkedList { func reverseRecursively() { func reverse(_ node: Node<T>?) -> Node<T>? { guard let head = node else { return node } if head.nextNode == nil { return head } let reversedHead = reverse(head.nextNode) head.nextNode?.nextNode = head head.nextNode = nil return reversedHead } firstNode = reverse(firstNode) } }
L'algorithme lui-même est «encapsulé» par une méthode du type liste lui-même, pour la commodité de l'appel.
Il semble plus court, mais, à mon avis, plus difficile à comprendre.
Nous appelons cette méthode sur le résultat du spread précédent et imprimons un nouveau résultat:
list.reverseRecursively() print(String(describing: list))
Il peut être vu à partir de la sortie que toutes les adresses dans la mémoire n'ont pas changé à nouveau, et les nœuds suivent maintenant dans l'ordre d'origine (c'est-à-dire qu'ils sont à nouveau «déployés»). Et cela signifie que nous avons à nouveau raison!
Conclusions
Si vous regardez attentivement les méthodes d'inversion (ou effectuez une expérience avec le comptage des appels), vous remarquerez que la boucle dans le premier cas et l'appel de méthode interne (récursif) dans le second cas se produisent une fois de moins que le nombre de nœuds dans la liste (dans notre cas, neuf fois). Vous pouvez également faire attention à ce qui se passe autour de la boucle dans le premier cas - la même séquence d'affectations - et au premier appel de méthode non récursif dans le second cas. Il s'avère que dans les deux cas le «cercle» est répété exactement dix fois pour une liste de dix nœuds. Ainsi, nous avons une
complexité linéaire pour les deux algorithmes -
O (n) .
De manière générale, les deux algorithmes décrits sont considérés comme les plus efficaces pour résoudre ce problème. En ce qui concerne la complexité de calcul, il n'est pas possible de trouver un algorithme avec une valeur inférieure: d'une manière ou d'une autre, vous devez «visiter» chaque nœud pour attribuer une nouvelle valeur au lien stocké à l'intérieur.
Une autre caractéristique qui mérite d'être mentionnée est la «complexité de la mémoire allouée». Les deux algorithmes proposés créent un nombre fixe de nouvelles variables (trois dans le premier cas et une dans le second). Cela signifie que la quantité de mémoire allouée ne dépend pas des caractéristiques quantitatives des données d'entrée et est décrite par une fonction constante - O (1).
Mais, en fait, dans le deuxième cas, ce n'est pas le cas. Le danger de récursivité est que de la mémoire supplémentaire est allouée pour chaque appel récursif sur la
pile . Dans notre cas, la profondeur de récursivité correspond à la quantité de données d'entrée.
Et finalement, j'ai décidé d'expérimenter un peu plus: de manière simple et primitive, j'ai mesuré le temps d'exécution absolu de deux méthodes pour une quantité différente de données d'entrée. Comme ça:
let startDate = Date().timeIntervalSince1970
Et voici ce que j'ai obtenu (ce sont les données brutes du
Playground ):
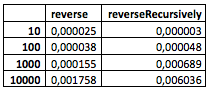
(Malheureusement, mon ordinateur n'a pas maîtrisé les plus grandes valeurs.)
Que peut-on voir sur la table? Rien de spécial pour le moment. Bien qu'il soit déjà visible que la méthode récursive se comporte un peu moins bien avec un nombre relativement petit de nœuds, mais quelque part entre 100 et 1000, elle commence à montrer mieux.
J'ai également essayé le même test simple dans un projet
«Xcode» à part entière. Les résultats sont les suivants:

Tout d'abord, il convient de mentionner que les résultats ont été obtenus après l'activation du mode d'optimisation «agressif» visant à la vitesse d'exécution (
-Ofast ), ce qui explique en partie pourquoi les nombres sont si petits. Il est également intéressant de noter que dans ce cas la méthode récursive s'est montrée un peu mieux, au contraire, que sur de très petites tailles de données d'entrée, et déjà sur une liste de 100 nœuds, la méthode perd. Sur 100 000, il a mis fin anormalement au programme.
Conclusion
J'ai essayé de couvrir un sujet plutôt classique du point de vue de mon langage de programmation préféré en ce moment, et j'espère que vous étiez curieux de suivre les progrès aussi bien que moi-même. Et je suis très heureux si vous avez réussi à apprendre quelque chose de nouveau également - alors j'ai définitivement perdu mon temps sur cet article (au lieu de m'asseoir et de regarder des
émissions de télévision ).
Si quelqu'un a envie de suivre mon activité sociale, voici un lien vers mon «Twitter» , où tout d'abord il y a des liens vers mes nouveaux posts et un peu plus.