Si l' article précédent était plus susceptible d'être prédéfini, il est maintenant temps de tester les capacités de parallélisation de Julia sur sa machine.

Traitement multicœur ou distribué

L'implémentation du calcul parallèle avec mémoire distribuée est assurée par le module Distributed dans le cadre de la bibliothèque standard fournie avec Julia. La plupart des ordinateurs modernes ont plus d'un processeur et plusieurs ordinateurs peuvent être regroupés. L'utilisation de la puissance de ces multiples processeurs vous permet d'effectuer de nombreux calculs plus rapidement. Les performances sont affectées par deux facteurs principaux: la vitesse des processeurs eux-mêmes et la vitesse de leur accès à la mémoire. Dans le cluster, il est évident que ce CPU aura l'accès le plus rapide à la RAM sur le même ordinateur (nœud). Peut-être encore plus surprenant, ces problèmes sont pertinents sur un ordinateur portable multicœur typique en raison des différences de vitesse de la mémoire principale et du cache. Par conséquent, un bon environnement multiprocesseur devrait vous permettre de contrôler la «propriété» d'une partie de la mémoire par un processeur spécifique. Julia fournit un environnement multiprocesseur basé sur la messagerie qui permet aux programmes de s'exécuter simultanément sur plusieurs processus dans différents domaines de mémoire.

L'implémentation de la messagerie de Julia est différente des autres environnements, tels que MPI [1] . La communication dans Julia est généralement «à sens unique», ce qui signifie que le programmeur doit contrôler explicitement un seul processus dans une opération à deux processus. De plus, ces opérations ne ressemblent généralement pas à «l'envoi d'un message» et à la «réception d'un message», mais ressemblent plutôt à des opérations d'un niveau supérieur, telles que les appels à des fonctions définies par l'utilisateur.

La programmation distribuée dans Julia repose sur deux primitives: les liaisons distantes et les appels distants . Un lien distant est un objet qui peut être utilisé à partir de n'importe quel processus pour faire référence à un objet stocké dans un processus particulier. Un appel distant est une demande d'un processus pour appeler une certaine fonction en fonction de certains arguments d'un autre (éventuellement le même) processus.

Les liaisons distantes se présentent sous deux formes: Future et RemoteChannel .

Un appel distant renvoie Future et le fait immédiatement; le processus qui a effectué l'appel passe à sa prochaine opération, tandis que l'appel distant a lieu ailleurs. Vous pouvez attendre que l'appel distant se termine avec la commande wait pour le Future renvoyé, et vous pouvez également obtenir la valeur complète du résultat à l'aide de fetch .

D'un autre côté, nous avons des RemoteChannels qui sont réécrits. Par exemple, plusieurs processus peuvent coordonner leur traitement en se référant au même canal distant. Chaque processus a un identifiant associé. Le processus qui fournit l'invite interactive Julia a toujours un identificateur de 1. Les processus utilisés par défaut pour les opérations simultanées sont appelés «travailleurs». Lorsqu'il n'y a qu'un seul processus, le processus 1 est considéré comme fonctionnant. Sinon, tous les processus autres que le processus 1 sont considérés comme des travailleurs.

Allons-y. julia -pn avec julia -pn postscript fournit n workflows sur l'ordinateur local. Il est généralement logique que n soit égal au nombre de threads CPU (cœurs logiques) sur la machine. Notez que l'argument -p charge implicitement le module distribué.

 julia> pwd() #     "C:\\Users\\User\\AppData\\Local\\Julia-1.1.0" julia> cd("C:/Users/User/Desktop") #   julia> run(`calc`) #     #     Windows. #      Process(`calc`, ProcessExited(0)) 

 using Distributed addprocs(2) 

 $ ./julia -p 2 julia> r = remotecall(rand, 2, 2, 2) Future(2, 1, 4, nothing) julia> s = @spawnat 2 1 .+ fetch(r) Future(2, 1, 5, nothing) julia> fetch(s) 2×2 Array{Float64,2}: 1.18526 1.50912 1.16296 1.60607 

Le premier argument de remotecall est la fonction appelée.
La plupart des programmes simultanés dans Julia ne font pas référence à des processus spécifiques ou au nombre de processus disponibles, mais un appel distant est considéré comme une interface de bas niveau qui fournit un contrôle plus précis.

Le deuxième argument de remotecall est l'identifiant du processus qui fera le travail, et les arguments restants seront passés à la fonction appelée. Comme vous pouvez le voir, dans la première ligne, nous avons demandé au processus 2 de construire une matrice aléatoire 2 par 2, et dans la deuxième ligne, nous avons demandé d'y ajouter 1. Le résultat des deux calculs est disponible en deux futures, r et s. La macro spawnat évalue l'expression dans le deuxième argument au processus spécifié dans le premier argument. Parfois, vous pouvez avoir besoin d'une valeur calculée à distance. Cela se produit généralement lorsque vous lisez à partir d'un objet distant pour obtenir les données nécessaires à la prochaine opération locale. Il existe une fonction remotecall_fetch pour remotecall_fetch . C'est équivalent à fetch (remotecall (...)) , mais plus efficace.

Souvenez-vous que getindex(r, 1,1) équivalent à r[1,1] , donc cet appel récupère le premier élément du futur r .

La remotecall appel distant remotecall pas particulièrement pratique. La macro @spawn facilite les @spawn . Il fonctionne avec une expression, pas une fonction, et choisit où effectuer l'opération pour vous:

 julia> r = @spawn rand(2,2) Future(2, 1, 4, nothing) julia> s = @spawn 1 .+ fetch(r) Future(3, 1, 5, nothing) julia> fetch(s) 2×2 Array{Float64,2}: 1.38854 1.9098 1.20939 1.57158 

Notez que nous avons utilisé 1 .+ Fetch(r) au lieu de 1 .+ r C'est parce que nous ne savons pas où le code sera exécuté, donc dans le cas général, il peut être nécessaire d'aller chercher pour déplacer r dans le processus d'ajout. Dans ce cas, @spawn est suffisamment intelligent pour effectuer des calculs pour le processus propriétaire de r , donc la récupération ne sera pas opérationnelle (aucun travail n'est effectué). (Il convient de noter que le spawn n'est pas intégré, mais défini dans Julia comme une macro. Vous pouvez définir vos propres constructions de ce type.)

Il est important de se rappeler qu'après l'extraction, Future mettra en cache sa valeur localement. D'autres appels à récupérer n'entraînent pas de saut de réseau. Une fois tous les contrats à terme référents sélectionnés, la valeur stockée supprimée est supprimée.

@async est similaire à @spawn , mais exécute les tâches uniquement dans le processus local. Nous l'utilisons pour créer une tâche de «flux» pour chaque processus. Chaque tâche sélectionne l'index suivant, qui doit être calculé, puis attend la fin du processus et se répète jusqu'à épuisement des index.

Notez que les tâches du chargeur ne démarrent pas avant que la tâche principale n'atteigne la fin du bloc @sync , après quoi elle passe le contrôle et attend que toutes les tâches locales se terminent avant de revenir de la fonction.

Comme pour la version 0.7 et supérieure, les tâches du feeder peuvent partager l'état via nextidx, car toutes sont exécutées dans le même processus. Même si les tâches sont planifiées ensemble, le blocage peut être requis dans certains contextes, comme avec les E / S asynchrones. Cela signifie que le changement de contexte se produit uniquement à des points bien définis: dans ce cas, lorsque remotecall_fetch est remotecall_fetch . Il s'agit de l'état actuel de l'implémentation, et il pourrait changer dans les futures versions de Julia, car il est conçu pour être en mesure d'exécuter jusqu'à N tâches dans M processus, ou M: N Threading . Ensuite, nous avons besoin d'un modèle pour obtenir / libérer des verrous pour nextidx , car il n'est pas sûr de permettre à plusieurs processus de lire et d'écrire des ressources en même temps.

Votre code doit être disponible pour tout processus qui l'exécute. Par exemple, à l'invite Julia, tapez ce qui suit:

 julia> function rand2(dims...) return 2*rand(dims...) end julia> rand2(2,2) 2×2 Array{Float64,2}: 0.153756 0.368514 1.15119 0.918912 julia> fetch(@spawn rand2(2,2)) ERROR: RemoteException(2, CapturedException(UndefVarError(Symbol("#rand2")) Stacktrace: [...] 

Le processus 1 connaissait la fonction rand2, mais pas le processus 2. Le plus souvent, vous téléchargerez du code à partir de fichiers ou de packages, et vous aurez une grande flexibilité pour contrôler les processus qui chargent le code. Considérez le fichier DummyModule.jl contenant le code suivant:

 module DummyModule export MyType, f mutable struct MyType a::Int end f(x) = x^2+1 println("loaded") end 

Pour référencer MyType dans tous les processus, DummyModule.jl doit être chargé dans chaque processus. Un appel à include ('DummyModule.jl') charge pour un seul processus. Pour le charger dans chaque processus, utilisez la macro @everywhere (exécutez Julia avec julia -p 2):

 julia> @everywhere include("DummyModule.jl") loaded From worker 3: loaded From worker 2: loaded 

Comme d'habitude, cela ne rend pas DummyModule accessible à tout processus nécessitant une utilisation ou une importation. De plus, lorsqu'un module factice est inclus dans la portée d'un processus, il n'est inclus dans aucun autre:

 julia> using .DummyModule julia> MyType(7) MyType(7) julia> fetch(@spawnat 2 MyType(7)) ERROR: On worker 2: UndefVarError: MyType not defined ⋮ julia> fetch(@spawnat 2 DummyModule.MyType(7)) MyType(7) 

Cependant, il est toujours possible, par exemple, d'envoyer MyType au processus qui a chargé le DummyModule, même s'il n'est pas dans la portée:

 julia> put!(RemoteChannel(2), MyType(7)) RemoteChannel{Channel{Any}}(2, 1, 13) 

Le fichier peut également être préchargé dans plusieurs processus au démarrage avec l'indicateur -L, et le script du pilote peut être utilisé pour contrôler les calculs:

 julia -p <n> -L file1.jl -L file2.jl driver.jl 

Le processus Julia qui exécute le script de pilote dans l'exemple ci-dessus a un identificateur de 1, tout comme le processus qui fournit l'invite interactive. Enfin, si DummyModule.jl n'est pas un fichier séparé, mais un package, l'utilisation de DummyModule chargera DummyModule.jl dans tous les processus, mais le transférera uniquement dans la portée du processus pour lequel l'utilisation a été appelée.

Lancement et gestion des workflows

L'installation de base de Julia prend en charge deux types de clusters:

• Le cluster local spécifié avec l'option -p, comme indiqué ci-dessus.
• Cluster des machines en utilisant l'option --machine-file. Celui-ci utilise la connexion ssh sans mot de passe pour démarrer les workflows Julia (sur le même chemin que l'hôte actuel) sur les machines spécifiées.

Les fonctions addprocs , rmprocs , worker et autres sont disponibles en tant qu'outil logiciel pour ajouter, supprimer et interroger des processus dans un cluster.

 julia> using Distributed julia> addprocs(2) 2-element Array{Int64,1}: 2 3 

Le module Distributed doit être explicitement chargé dans le processus principal avant d'appeler addprocs . Il devient automatiquement disponible pour les workflows. Notez que les travailleurs ~/.julia/config/startup.jl pas le script de démarrage ~/.julia/config/startup.jl et ne synchronisent pas leur état global (tels que les variables globales, les définitions de nouvelles méthodes et les modules chargés) avec les autres processus en cours d'exécution. D'autres types de clusters peuvent être pris en charge en écrivant votre propre ClusterManager , comme décrit ci-dessous dans la section ClusterManager .

Actions de données

L'envoi de messages et le déplacement de données constituent l'essentiel des frais généraux d'un programme distribué. La réduction du nombre de messages et de la quantité de données envoyées est essentielle pour atteindre les performances et l'évolutivité. Pour cela, il est important de comprendre le mouvement de données effectué par les différentes constructions de programmation distribuée de Julia.

fetch peut être considéré comme une opération de déplacement de données explicite, car il demande directement le déplacement d'un objet vers la machine locale. @spawn (et plusieurs constructions associées) déplace également les données, mais ce n'est pas si évident, donc on peut l'appeler une opération de déplacement de données implicite. Considérez ces deux approches pour construire et mettre au carré une matrice aléatoire:

Temps de trajet:

 julia> A = rand(1000,1000); julia> Bref = @spawn A^2; [...] julia> fetch(Bref); 

deuxième méthode:

 julia> Bref = @spawn rand(1000,1000)^2; [...] julia> fetch(Bref); 

La différence semble insignifiante, mais en fait elle est assez importante en raison du comportement de @spawn . Dans la première méthode, une matrice aléatoire est construite localement, puis envoyée à un autre processus, où elle est au carré. Dans la deuxième méthode, une matrice aléatoire est construite et mise au carré sur un autre processus. Par conséquent, la deuxième méthode envoie beaucoup moins de données que la première. Dans cet exemple de jouet, les deux méthodes sont faciles à distinguer et à choisir. Cependant, dans un vrai programme, la conception d'un mouvement de données peut être très coûteuse et probablement une certaine mesure.

Par exemple, si le premier processus a besoin de la matrice A, alors la première méthode pourrait être meilleure. Ou, si le calcul de A est coûteux et utilise uniquement le processus actuel, le déplacer vers un autre processus peut être inévitable. Ou, si le processus actuel a très peu en commun entre le spawn et le fetch(Bref) , il pourrait être préférable d'éliminer complètement la concurrence. Ou imaginez que le rand(1000, 1000) remplacé par une opération plus coûteuse. Ensuite, il peut être judicieux d'ajouter une autre instruction de spawn juste pour cette étape.

Variables globales

Les expressions exécutées à distance via le spawn, ou les fermetures spécifiées pour une exécution à distance à l'aide de remotecall , peuvent faire référence à des variables globales. Les liaisons globales du module Main sont gérées un peu différemment des liaisons globales des autres modules. Considérez l'extrait de code suivant:

 A = rand(10,10) remotecall_fetch(()->sum(A), 2) 

Dans ce cas, la sum DOIT être définie dans le processus distant. Notez que A est une variable globale définie dans l'espace de travail local. Le travailleur 2 n'a pas de variable nommée A dans la section Main . L'envoi de la fonction de fermeture () -> sum(A) pour le travailleur 2 entraîne la Main.A sur 2. Main.A continue d'exister sur le travailleur 2 même après avoir renvoyé l'appel remotecall_fetch .

Les appels distants avec des références globales intégrées (dans le module principal uniquement) gèrent les variables globales comme suit:

• De nouvelles liaisons globales sont créées sur les postes de travail de destination si elles sont référencées dans le cadre d'un appel distant.
• Les constantes globales sont également déclarées comme constantes sur les nœuds distants.
• Les globaux ne sont soumis à nouveau à l'employé cible que dans le contexte d'un appel distant et uniquement si sa valeur a changé. En outre, le cluster ne synchronise pas les liaisons globales entre les nœuds. Par exemple:

 A = rand(10,10) remotecall_fetch(()->sum(A), 2) # worker 2 A = rand(10,10) remotecall_fetch(()->sum(A), 3) # worker 3 A = nothing 

L'exécution du fragment ci-dessus conduit au fait que Main.A sur l'employé 2 a une valeur différente de Main.A sur l'employé 3, tandis que la valeur de Main.A sur le nœud 1 est nulle.

Comme vous l'avez probablement compris, bien que la mémoire associée aux variables globales puisse être collectée lorsqu'elles sont réaffectées au périphérique maître, de telles actions ne sont pas prises pour les travailleurs, car les liaisons continuent de fonctionner. clair! peut être utilisé pour réaffecter manuellement certaines variables globales à nothing si elles ne sont plus nécessaires. Cela libérera toute la mémoire qui leur est associée dans le cadre du cycle normal de collecte des ordures. Par conséquent, les programmes doivent être prudents lors de l'accès aux variables globales dans les appels distants. En fait, dans la mesure du possible, il vaut mieux les éviter du tout. Si vous devez référencer des variables globales, envisagez d'utiliser des blocs let pour localiser des variables globales. Par exemple:

 julia> A = rand(10,10); julia> remotecall_fetch(()->A, 2); julia> B = rand(10,10); julia> let B = B remotecall_fetch(()->B, 2) end; julia> @fetchfrom 2 InteractiveUtils.varinfo() name size summary ––––––––– ––––––––– –––––––––––––––––––––– A 800 bytes 10×10 Array{Float64,2} Base Module Core Module Main Module 

Il est facile de voir que la variable globale A définie sur le travailleur 2, mais B écrite en tant que variable locale, et donc la liaison pour B n'existe pas sur le travailleur 2.

Boucles parallèles

Heureusement, de nombreux calculs de concurrence utiles ne nécessitent pas de mouvement de données. Un exemple typique est une simulation Monte Carlo, où plusieurs processus peuvent simultanément traiter des tests de simulation indépendants. Nous pouvons utiliser @spawn pour retourner des pièces en deux processus. Écrivez d'abord la fonction suivante dans count_heads.jl :

 function count_heads(n) c::Int = 0 for i = 1:n c += rand(Bool) end c end 

La fonction count_heads additionne simplement n bits aléatoires. Voici comment nous pouvons faire quelques tests sur deux machines et additionner les résultats:

 julia> @everywhere include_string(Main, $(read("count_heads.jl", String)), "count_heads.jl") julia> a = @spawn count_heads(100000000) Future(2, 1, 6, nothing) julia> b = @spawn count_heads(100000000) Future(3, 1, 7, nothing) julia> fetch(a)+fetch(b) 100001564 

Cet exemple illustre un modèle de programmation parallèle puissant et fréquemment utilisé. De nombreuses itérations sont effectuées indépendamment dans plusieurs processus, puis leurs résultats sont combinés à l'aide d'une fonction. Le processus d'union est appelé réduction, car il réduit généralement le rang du tenseur: le vecteur de nombres est réduit à un nombre, ou la matrice est réduite à une ligne ou une colonne, etc. Dans le code, cela ressemble généralement à ceci: motif x = f(x, v [i]) , où x est la batterie, f est la fonction de réduction et v[i] est les éléments à réduire.

Il est souhaitable que f soit associatif pour qu'il importe peu dans quel ordre les opérations sont effectuées. Veuillez noter que notre utilisation de ce modèle avec count_heads peut être généralisée. Nous avons utilisé deux déclarations d' spawn explicites, ce qui limite la concurrence à deux processus. Pour fonctionner sur un nombre quelconque de processus, nous pouvons utiliser un parallèle for boucle fonctionnant en mémoire distribuée, qui peut être écrit dans Julia en utilisant distribué , par exemple:

 nheads = @distributed (+) for i = 1:200000000 Int(rand(Bool)) end 

( (+) ). . .

, for , . , , , . , , . , :

 a = zeros(100000) @distributed for i = 1:100000 a[i] = i end 

, . , . , Shared Arrays , , :

 using SharedArrays a = SharedArray{Float64}(10) @distributed for i = 1:10 a[i] = i end 

«» , :

 a = randn(1000) @distributed (+) for i = 1:100000 f(a[rand(1:end)]) end 

f , . , , . , Future , . Future , fetch , , @sync , @sync distributed for .

, (, , ). , , Julia pmap . , :

 julia> M = Matrix{Float64}[rand(1000,1000) for i = 1:10]; julia> pmap(svdvals, M); 

pmap , . , distributed for , , , . pmap , distributed . distributed for .

(Shared Arrays)

Shared Arrays . DArray , SharedArray . DArray , ; , SharedArray .

SharedArray — , , . Shared Array SharedArrays , . SharedArray ( ) , , . SharedArray , . , Array , SharedArray , sdata . AbstractArray sdata , sdata Array . :

 SharedArray{T,N}(dims::NTuple; init=false, pids=Int[]) 

N - T dims , pids . , , pids ( , ).

init initfn(S :: SharedArray) , . , init , .

:

 julia> using Distributed julia> addprocs(3) 3-element Array{Int64,1}: 2 3 4 julia> @everywhere using SharedArrays julia> S = SharedArray{Int,2}((3,4), init = S -> S[localindices(S)] = myid()) 3×4 SharedArray{Int64,2}: 2 2 3 4 2 3 3 4 2 3 4 4 julia> S[3,2] = 7 7 julia> S 3×4 SharedArray{Int64,2}: 2 2 3 4 2 3 3 4 2 7 4 4 

SharedArrays.localindices . , , :

 julia> S = SharedArray{Int,2}((3,4), init = S -> S[indexpids(S):length(procs(S)):length(S)] = myid()) 3×4 SharedArray{Int64,2}: 2 2 2 2 3 3 3 3 4 4 4 4 

, , . Par exemple:

 @sync begin for p in procs(S) @async begin remotecall_wait(fill!, p, S, p) end end end 

. pid , , ( S ), pid .

«»:

 q[i,j,t+1] = q[i,j,t] + u[i,j,t] 

, , , , , : q [i,j,t] , q[i,j,t+1] , , , q[i,j,t] , q[i,j,t+1] . . . , (irange, jrange) , :

 julia> @everywhere function myrange(q::SharedArray) idx = indexpids(q) if idx == 0 # This worker is not assigned a piece return 1:0, 1:0 end nchunks = length(procs(q)) splits = [round(Int, s) for s in range(0, stop=size(q,2), length=nchunks+1)] 1:size(q,1), splits[idx]+1:splits[idx+1] end 

:

 julia> @everywhere function advection_chunk!(q, u, irange, jrange, trange) @show (irange, jrange, trange) # display so we can see what's happening for t in trange, j in jrange, i in irange q[i,j,t+1] = q[i,j,t] + u[i,j,t] end q end 

SharedArray

 julia> @everywhere advection_shared_chunk!(q, u) = advection_chunk!(q, u, myrange(q)..., 1:size(q,3)-1) 

, :

 julia> advection_serial!(q, u) = advection_chunk!(q, u, 1:size(q,1), 1:size(q,2), 1:size(q,3)-1); 

@distributed :

 julia> function advection_parallel!(q, u) for t = 1:size(q,3)-1 @sync @distributed for j = 1:size(q,2) for i = 1:size(q,1) q[i,j,t+1]= q[i,j,t] + u[i,j,t] end end end q end; 

, :

 julia> function advection_shared!(q, u) @sync begin for p in procs(q) @async remotecall_wait(advection_shared_chunk!, p, q, u) end end q end; 

SharedArray , ( julia -p 4 ):

 julia> q = SharedArray{Float64,3}((500,500,500)); julia> u = SharedArray{Float64,3}((500,500,500)); 

JIT- @time :

 julia> @time advection_serial!(q, u); (irange,jrange,trange) = (1:500,1:500,1:499) 830.220 milliseconds (216 allocations: 13820 bytes) julia> @time advection_parallel!(q, u); 2.495 seconds (3999 k allocations: 289 MB, 2.09% gc time) julia> @time advection_shared!(q,u); From worker 2: (irange,jrange,trange) = (1:500,1:125,1:499) From worker 4: (irange,jrange,trange) = (1:500,251:375,1:499) From worker 3: (irange,jrange,trange) = (1:500,126:250,1:499) From worker 5: (irange,jrange,trange) = (1:500,376:500,1:499) 238.119 milliseconds (2264 allocations: 169 KB) 

advection_shared! , , .

, . , , .
, , , .

- Julia

, , , .

$$$\pi = 3.14159265...$ , , -. $$$\ pi$ , $$$S = \pi r^2$ où $$$r$ — . - $$$\ pi$ , .. $$$[−1,1]^2$ $$$x-y$ , .

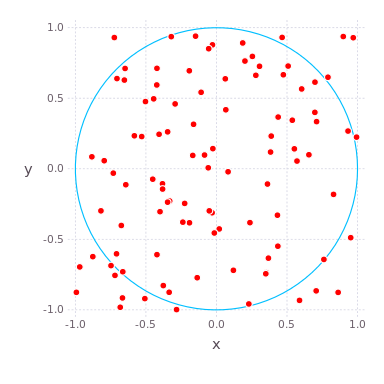
( $$$S=\pi$ , $$$r = 1$ ) ( $$$A = 4$ ) $$$\pi/4$ , , , . , $$$\ pi$ , . compute_pi (N) , $$$\ pi$ , $$$N$ .

 function compute_pi(N::Int) # counts number of points that have radial coordinate < 1, ie in circle n_landed_in_circle = 0 for i = 1:N x = rand() * 2 - 1 # uniformly distributed number on x-axis y = rand() * 2 - 1 # uniformly distributed number on y-axis r2 = x*x + y*y # radius squared, in radial coordinates if r2 < 1.0 n_landed_in_circle += 1 end end return n_landed_in_circle / N * 4.0 end 

, , $$$\ pi$ . : , , 25 .

Julia Pi.jl ( Sublime Text , ):

 C:\Users\User\AppData\Local\Julia-1.1.0\bin\julia -p 4 julia> include("C:/Users/User/Desktop/Pi.jl") 

 using Distributed addprocs(4) 

Jupyter

 @everywhere function compute_pi(N::Int) n_landed_in_circle = 0 # counts number of points that have radial coordinate < 1, ie in circle for i = 1:N x = rand() * 2 - 1 # uniformly distributed number on x-axis y = rand() * 2 - 1 # uniformly distributed number on y-axis r2 = x*x + y*y # radius squared, in radial coordinates if r2 < 1.0 n_landed_in_circle += 1 end end return n_landed_in_circle / N * 4.0 end function parallel_pi_computation(N::Int; ncores::Int=4) #       sum_of_pis = @distributed (+) for i=1:ncores compute_pi(ceil(Int, N / ncores)) end return sum_of_pis / ncores # average value end # ceil (T, x)     #  T,     x. 

, :

 julia> @time parallel_pi_computation(1000000000, ncores = 1) 6.818123 seconds (1.96 M allocations: 99.838 MiB, 0.42% gc time) 3.141562892 julia> @time parallel_pi_computation(1000000000, ncores = 1) 5.081638 seconds (1.12 k allocations: 62.953 KiB) 3.141657252 julia> @time parallel_pi_computation(1000000000, ncores = 2) 3.504871 seconds (1.84 k allocations: 109.382 KiB) 3.1415942599999997 julia> @time parallel_pi_computation(1000000000, ncores = 4) 3.093918 seconds (1.12 k allocations: 71.938 KiB) 3.1416889400000003 julia> pi ? = 3.1415926535897... 

JIT - — . , Julia . , ( Multi-Threading, Atomic Operations, Channels Coroutines).

Liens utiles

, , . MPI.jl MPI ,
DistributedArrays.jl .
GPU, :

1. ( C) OpenCL.jl CUDAdrv.jl OpenCL CUDA.
2. ( Julia) CUDAnative.jl CUDA .
3. , , CuArrays.jl CLArrays.jl
4. , ArrayFire.jl GPUArrays.jl
5. -
7. Kynseed

, , . !