Automates cellulaires en évolution

Connectez les automates cellulaires avec l'algorithme génétique et voyez ce qui se passe.

L'article contient du Gif (trafic!) Et des images contrastées. Les épileptiques peuvent avoir une crise d'épilepsie.

Règles pour les automates cellulaires

L'automate cellulaire le plus simple est un automate cellulaire unidimensionnel (il existe également des automates zéro dimensionnels - nous en parlerons ci-dessous). Dans un automate cellulaire unidimensionnel, nous avons un réseau unidimensionnel, dont les cellules (cellules) peuvent prendre l'un des deux états (1/0, vrai / faux, blanc / noir, vivant / mort). L'état suivant de la cellule dans le réseau est déterminé par l'état actuel de la cellule et l'état de deux cellules voisines, selon une règle.

Le total existe $$ combinaisons d'états de cellules et de deux cellules voisines:



Ensuite, pour chacune des combinaisons, nous notons l'état de la cellule pour la prochaine itération (pour l'état suivant de l'automate):



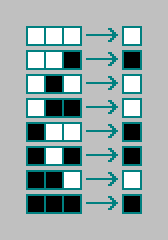
Vous avez une règle pour un automate cellulaire. Les règles pour les automates cellulaires unidimensionnels sont codées sur 8 bits («code tungstène»). Le total existe $$ automates cellulaires élémentaires:



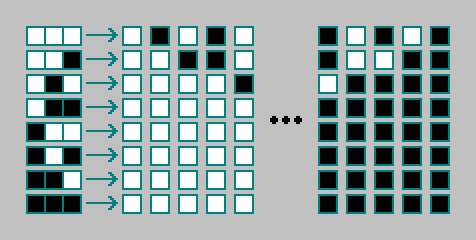
256 machines peuvent être triées manuellement. Nous ne nous attarderons pas sur eux. Nous calculons le nombre de règles existantes pour les automates cellulaires bidimensionnels.

Un automate cellulaire bidimensionnel utilise un réseau bidimensionnel. Chaque cellule a 8 voisins à proximité de Moore (il y a aussi un quartier von Neumann dans lequel les cellules diagonales ne sont pas prises en compte. Nous ne le considérerons pas dans l'article):



Pour plus de commodité, nous écrivons les cellules sur une ligne (nous utiliserons l'ordre sélectionné plus loin dans l'article):



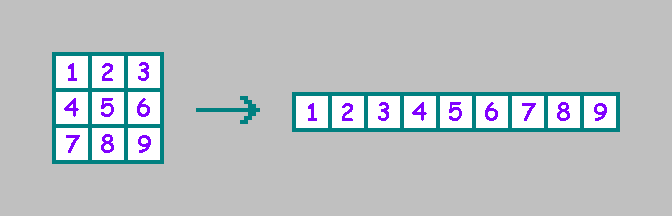
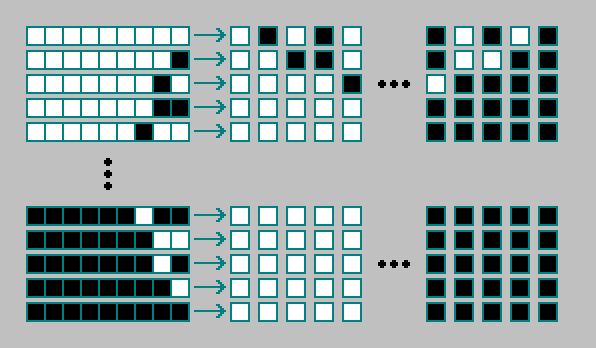
Pour un automate cellulaire bidimensionnel, il existe $$ combinaisons d'états de cellules et de 8 cellules voisines:



La règle pour un automate cellulaire bidimensionnel est codée avec 512 bits. Le total existe $$$2 ^ {512}$ automates cellulaires bidimensionnels:



Numéro:

$$

plus d' atomes dans l'univers observable ( $$ )
Manuellement, ce nombre de machines ne peut pas être trié. Si nous regardions un automate chaque seconde - pendant l'existence de l'Univers, nous aurions réussi à tout regarder $$$\ environ 4,35 \ times10 ^ {17}$ machines automatiques.

L'énumération simple ne fonctionne pas, mais à l'aide d'un algorithme génétique, nous pouvons trouver des automates qui correspondent le mieux à certains critères prédéfinis.

Nous programmerons en JavaScript. Tous les fragments de code sont cachés sous des spoilers afin de ne pas confondre les lecteurs qui ne sont pas familiers avec les langages de programmation.

Automate cellulaire bidimensionnel

Nous écrivons un automate cellulaire bidimensionnel avec une règle aléatoire. Nous allons stocker la règle dans le tableau de règles, dont la longueur rulesize = 512:


Ensuite, remplissez l'état initial de la machine avec une maison aléatoire:


(ici et plus loin dans l'article, comme la largeur et la hauteur de la machine, un nombre aléatoire est pris - pas très grand et pas très petit nombre impair 89)

La fonction qui calcule l'état suivant de l'automate se présente comme suit (pour ne pas le salir, il a supprimé l'initialisation du canevas):


Les variables xm et xp stockent les coordonnées X du voisin de gauche et du voisin de droite (x moins et x plus). Les variables ym et yp stockent les coordonnées Y correspondantes.

Ici:


nous définissons des conditions aux limites périodiques (le champ de l'automate est la surface du tore).

Suivant:


dans l'ordre ci-dessus, écrivez le contenu des cellules dans une chaîne. Nous traduisons la chaîne en nombre décimal. Pour cette combinaison, nous trouvons dans le tableau de règles l'état que doit prendre la cellule avec les coordonnées x et y.


Après toutes les itérations, remplacez l'état précédent de l'automate par un nouveau:


Nous dessinons un automate en utilisant la fonction setInterval:


Exécuter dans le navigateur

Je recommande de démarrer la machine avec des règles aléatoires 10-20 fois avant de continuer la lecture de l'article.

Nous pouvons faire fonctionner la machine très longtemps avec différentes règles aléatoires. L'image que nous obtenons ne diffère pas de l'image sur l'écran du téléviseur en l'absence de signal:



Passons maintenant à la configuration de notre «TV» en utilisant l'algorithme génétique.

Algorithme génétique

La taille de la population initiale est de 200 machines (individus). Pour les règles, au lieu d'un tableau de règles unidimensionnel, nous utiliserons un tableau de population bidimensionnel. Le premier indice (n) est le nombre d'individus dans la population.


Le tableau de fitness contient les coefficients de fitness de chaque individu. Ce tableau est rempli dans le processus de sélection. Après la sélection, nous entamons le processus évolutif.

Processus évolutif

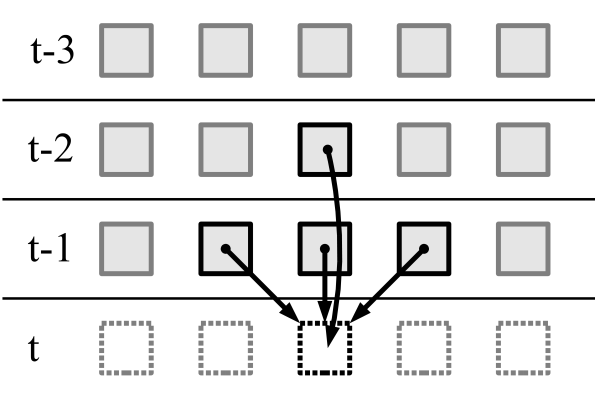
Dans notre population, nous prenons la moitié des individus les plus adaptés (selon le coefficient de fitness). La moitié restante est détruite. Ensuite, nous prenons deux individus survivants et les croisons.



Pour traverser, sélectionnez une position aléatoire dans les génotypes de deux ancêtres. Avant cette position, nous prenons les gènes d'un ancêtre, après cette position - d'un autre. Nous avons mis les gènes sélectionnés dans le génotype à un descendant. Les gènes restants sont pour un autre. Nous plaçons deux ancêtres et deux descendants dans une nouvelle population. En même temps, chaque individu participe une fois à la traversée.

Mutations. Avec une probabilité de 5%, un gène sélectionné au hasard mute (s'inverse) chez chaque individu. Si vous augmentez la probabilité de mutations, il y aura plus de mutants réussis, mais en même temps, un mutant réussi peut ne pas avoir le temps de laisser une progéniture réussie avant de muter à nouveau sans succès. Nous reviendrons sur cette question plus tard.

Sélection naturelle

Avant de commencer le processus évolutif, une sélection doit être effectuée. La sélection peut être à la fois naturelle et artificielle. La sélection artificielle se fait manuellement - à ce sujet un peu plus tard. Pour la sélection naturelle, nous allons définir certains critères et sélectionner les machines qui correspondent le mieux aux critères donnés.

Quels critères peuvent être déterminés à l'avance? Prenez le plus simple. Notre "TV" clignote trop. Nous sauvons deux états de l'automate cellulaire - à 99 et à 100 itérations. Comptez le nombre de cellules qui n'ont pas changé. Le nombre résultant sera utilisé comme coefficient de fitness. Évidemment, un critère ne nous suffit pas. Il est facile de sélectionner manuellement l'automate qui répondra le mieux au critère donné: l'automate [0,0,0, ..., 0] et l'automate [1,1,1, ..., 1]. À la première itération, ces deux automates sont remplis de zéros ou de uns et arrêtent de changer leur état. Nous définissons le deuxième critère: la différence entre le nombre de 0 et 1 (cellules) dans la machine ne dépasse pas 100 (le nombre est pris "du bulldozer").

array1 - état de l'automate à la 99ème itération. array2 - à la 100e itération:


Nous commençons. La solution optimale a été trouvée au 421e cycle d'évolution. Sur le graphique, vous pouvez voir la progression:



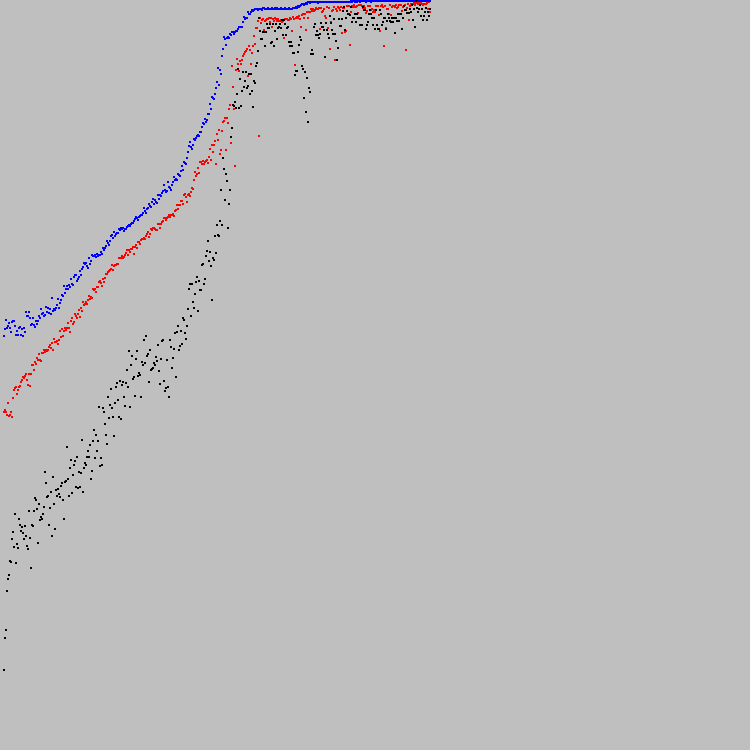
Le graphique est mis à l'échelle le long de l'axe Y. Le point inférieur est 0, le point le plus élevé est 7921. De toute évidence, 7921 est la solution optimale (toutes les cellules de la machine 89x89 répondent au critère spécifié). Après 100 itérations, aucune cellule ne change d'état.

Les points bleus sur le graphique sont le meilleur individu de la population. Les rouges sont les pires (seuls les individus répondant au deuxième critère sont pris en compte). Points noirs - le coefficient moyen de fitness pour toute la population (en tenant compte des individus qui ne répondent pas au deuxième critère). Le deuxième critère (l'équilibre entre le blanc et le noir) est très difficile. Certains automates ne répondent pas au deuxième critère même après 421 cycles d'évolution. Par conséquent, les points noirs sont en dessous du rouge.

Le patrimoine génétique de la population (individus le long de l'axe Y, gènes le long de l'axe X):



Voyons quelle chaîne notre «TV» a capturée:



La solution trouvée n'est pas la seule optimale. Si nous réexécutons l'évolution (avec des génotypes initiaux aléatoires), nous trouverons d'autres solutions optimales. L'un d'eux:



Modifiez les critères de sélection.

Nous considérerons le nombre de cellules pour lesquelles un motif apparaît au voisinage de Moore d'ordre 2. Prenons le modèle le plus simple:



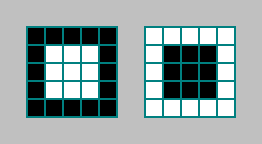
Ce critère est intéressant en ce que nous vérifions 25 cellules, tandis que l'automate calcule l'état de la cellule en fonction des états de 9 cellules.

Le critère est très strict. Si nous prenons un automate aléatoire, après 100 itérations, cela ressemble à ceci:



Pas une seule cellule dans un tel automate ne répond au critère donné. Par conséquent, nous adoucissons un peu le critère:

1. Faisons une erreur dans le motif.
2. Nous ne rechercherons pas le motif à la dernière itération, mais aux 50 dernières itérations.

Le deuxième critère (l'équilibre entre le blanc et le noir) est supprimé.

Nous commençons. Graphique:



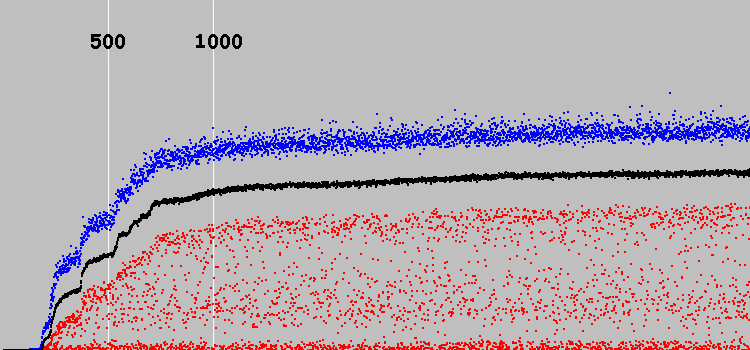
L'axe des y est arbitraire. (Dans la machine précédente, la solution optimale est 7921. Dans cette machine, environ 30.)
Axe X - 3569 cycles d'évolution. Deux lignes verticales blanches marquent 500 et 1000 cycles d'évolution.
Les points bleus - le meilleur individu de la population, le rouge - le pire, le noir - le rapport moyen pour l'ensemble de la population.

La solution a été trouvée au cours des 500 premiers cycles d'évolution. Les 500 prochains cycles, la solution s'améliore. Et puis le système cesse pratiquement d'évoluer.

Dans les trois images ci-dessous: 500 cycles, 1000 cycles et 3569 cycles d'évolution:



Pool de gènes (3569):



En dynamique:



Dans l'image ci-dessous, vous pouvez voir comment l'oscillateur (planeur) est formé dans cette machine:



Nous pouvons démarrer la machine avec l'état initial dans lequel une cellule est remplie. Ensuite, corrigez toutes les combinaisons de cellules trouvées dans les itérations suivantes de l'automate. Un tableau de gènes (le génotype d'un automate) est un tableau de toutes les combinaisons possibles. N'ayant isolé que les combinaisons qui se produisent, nous pouvons facilement noter tous les gènes impliqués dans la formation de l'oscillateur. Les barres grises sont des gènes qui ne participent pas à la formation de l'oscillateur:



Les mutations de ces gènes ne prennent pas racine car elles perturbent la formation des patrons.

Dans notre machine, un motif (carré) est formé uniquement autour d'une cellule noire. Essayons de démarrer le processus évolutif avec le deuxième critère: la différence entre le nombre de cellules blanches et noires ne dépasse pas 400.

Nous commençons 3569 cycles d'évolution. Graphique:



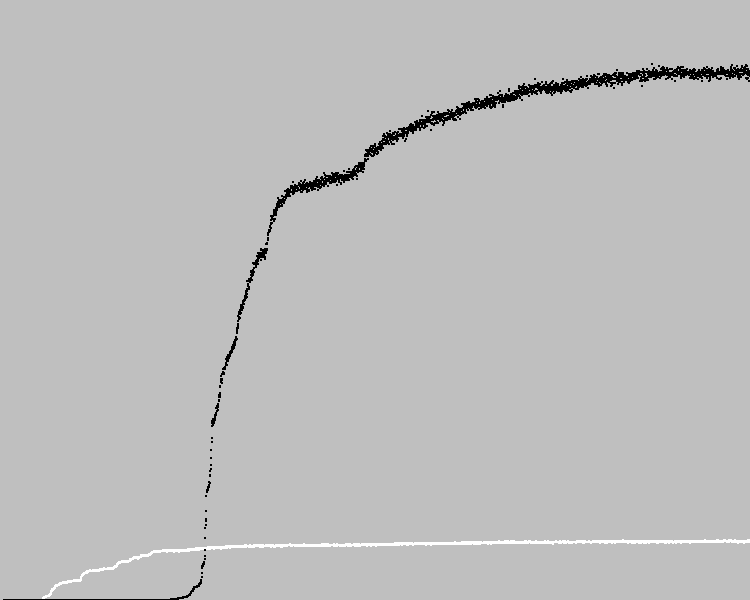
Les points noirs sur le graphique représentent le coefficient de fitness moyen dans une population. Points blancs - le coefficient moyen de fitness de la machine précédente. Trouvé une solution avec une erreur dans le modèle.

Pool de gènes:



100 premières itérations:



Dernière (100) itération:



Un peu pas le résultat que l'on attendait. Il y a des carrés noirs, blancs - non. Resserrer le deuxième critère: la différence entre le nombre de cellules blanches et noires ne dépasse pas 100.

Nous commençons 14865 cycles d'évolution.
Le graphique compare les coefficients de fitness moyens des populations. Les points bleus sont notre mitrailleuse. Le blanc et le noir sont des machines précédentes.



Un automate évolue si vigoureusement qu'il peut sembler qu'il n'évolue pas du tout. Le deuxième graphique est mis à l'échelle le long de l'axe Y. Deux lignes blanches - 500 et 1000 cycles.



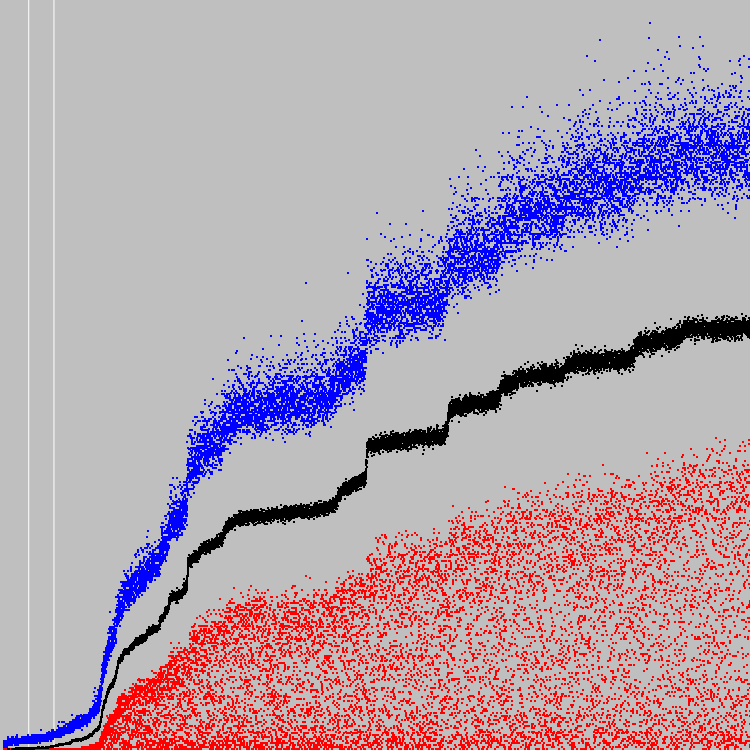
Chez le meilleur individu, en moyenne, 6 cellules correspondent à un critère donné.

Regardons une machine aléatoire d'une population.
50 itérations:



Dernière (50) itération:



Aucun résultat acceptable trouvé. Le deuxième critère complique la recherche, nous allons donc la refuser (nous ne l'utiliserons pas plus loin dans l'article). Laissons ce modèle et recherchons quelques autres modèles.

Motif:



Nous commençons. 3000 cycles d'évolution. Graphique:



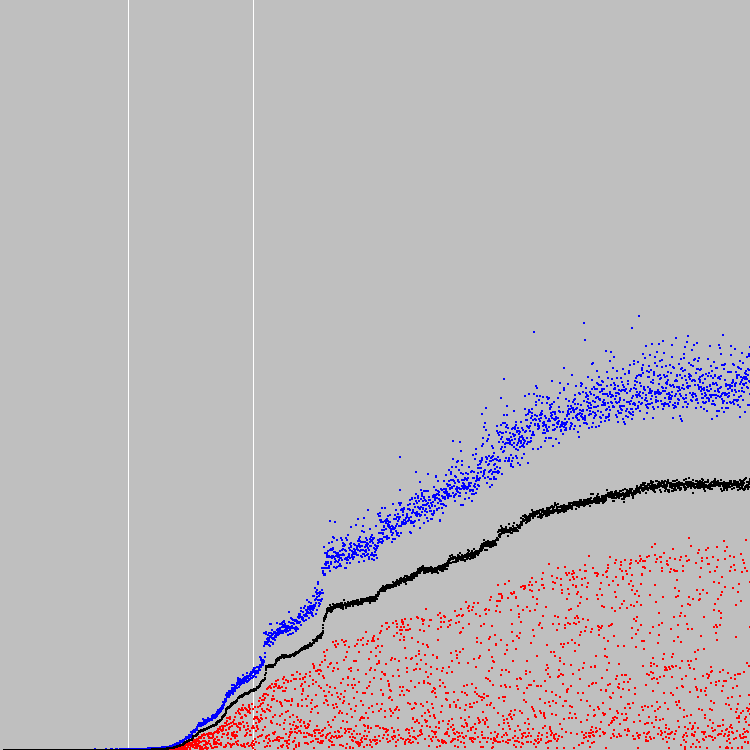
Pool de gènes:



En dynamique (100 itérations):



Dernière (100) itération:



Motif:



Dans les machines précédentes, nous avons permis de faire une erreur dans le motif. Cette fois, recherchons le motif exact.

Nous commençons 4549 cycles d'évolution. Graphique:



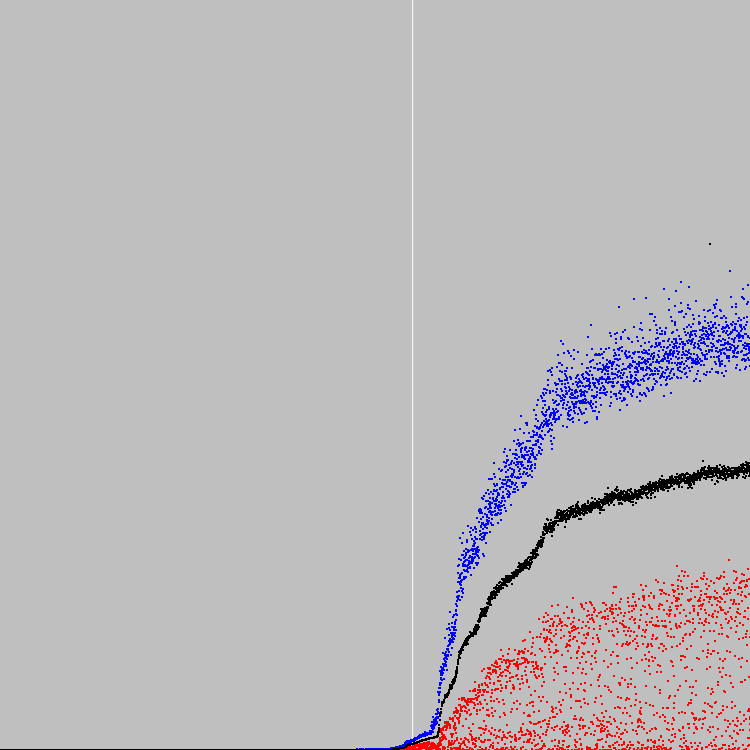
Ligne verticale blanche - 2500 cycles d'évolution. À ce stade (un peu plus tôt), la forme physique de la population a commencé à croître rapidement. A sauvé la population pour rechercher une solution provisoire. La solution intermédiaire s'est avérée beaucoup plus intéressante que la solution du 4549e cycle d'évolution.

Solution trouvée sur le 4549e cycle d'évolution:



Il y a 100 itérations sur Gif. Après un certain nombre d'itérations (environ 500-2000), l'état de l'automate est presque complètement ordonné (la hauteur et la largeur de l'automate sont spécialement choisies par des nombres impairs pour que l'automate ne puisse pas être complètement ordonné):



Un automate de dimensions égales de côtés, après un certain nombre d'itérations, prend un état entièrement ordonné. Automatique 90x90, environ 1200 itérations:



Solution intermédiaire (trouvée au 2500e cycle d'évolution):



Cet automate est également capable de transformer un certain état chaotique initial en un certain état ordonné fini (l'état ordonné final est le décalage du motif le long de l'axe X vers la gauche + plusieurs cellules d'oscillateur).

La machine 16x16 a trié en environ 100 itérations:



32x32 - environ 1000 itérations:



64x64 - environ 6000 itérations:



90x90 - environ 370000 itérations:



11x11 (dimensions impaires du champ automate) - environ 178700 itérations:



Le fusil d'assaut 13x13 n'a pas commandé dans un délai acceptable.

Dans l'image ci-dessous, la machine sur le champ 256x256 à la 100 000e itération:



Je recommande de regarder cet automate en dynamique sur un grand champ - il est très intéressant d'observer le processus d'auto-organisation du chaos dans cet automate: exécuté dans un navigateur

Pool de gènes de la population intermédiaire:



Le redémarrage du processus évolutif vous permet de trouver d'autres solutions. L'un d'eux:





Un autre schéma:



Lors de la recherche d'un motif, faisons encore une erreur (sans erreur, le système avec le motif sélectionné n'évolue pas).

Nous commençons. 5788 cycles d'évolution. Graphique:



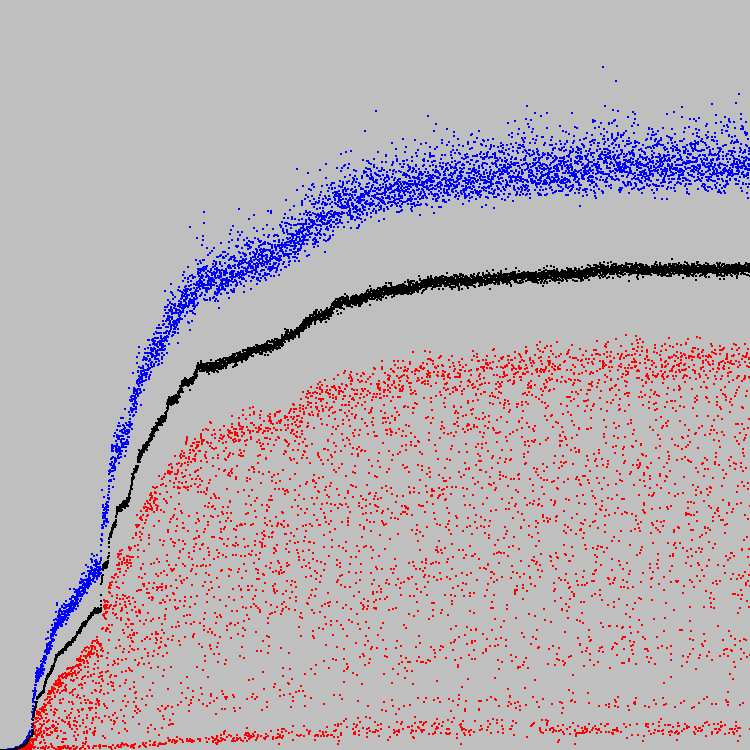
L'échelle est arbitraire.

Pool de gènes:



En dynamique:



L'état ordonné de l'automate (motif déplacé vers le haut le long de l'axe Y + plusieurs cellules oscillantes):



Il est beaucoup plus intéressant d'observer non pas la machine elle-même, mais les mutants qui apparaissent dans cette population:



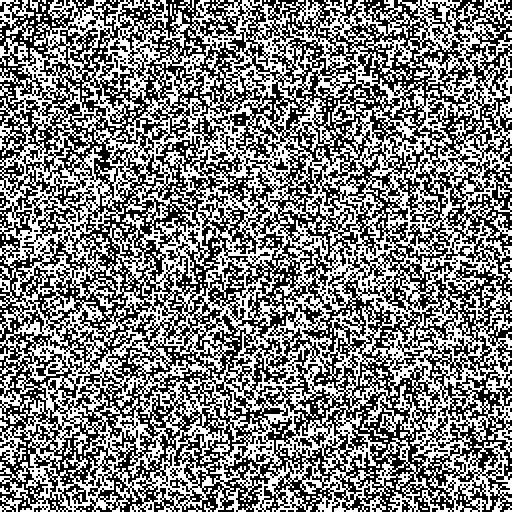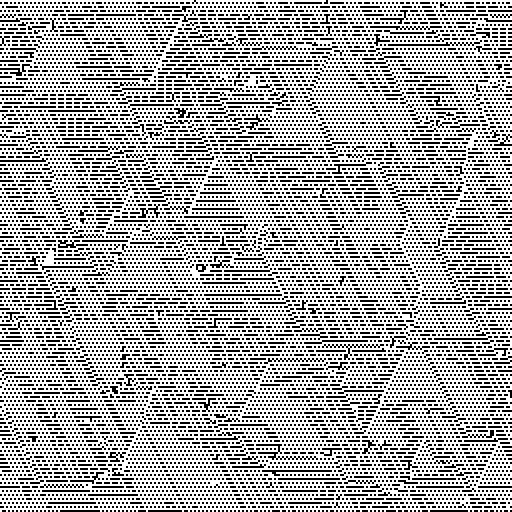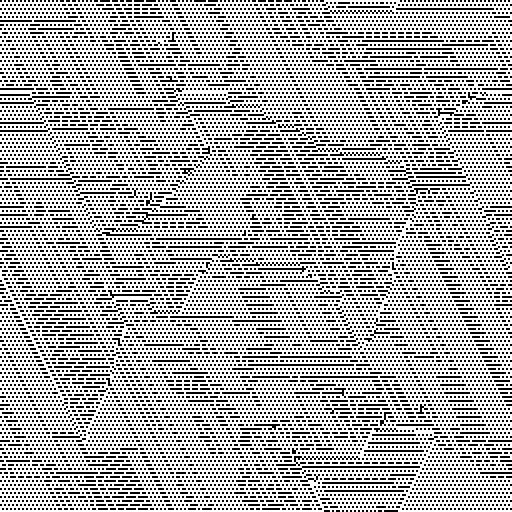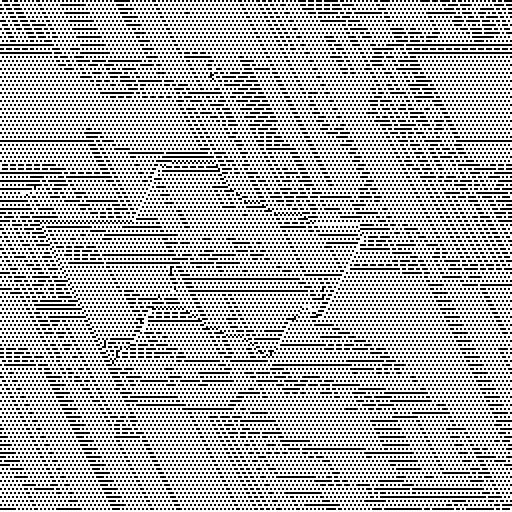
Sur Gif, la machine est 256x256. 200 itérations. Les itérations restantes peuvent être consultées dans le navigateur .

On pourrait finir avec la sélection naturelle et passer à l'artificiel, mais je veux montrer combien $$$2 ^ {512}$ un nombre énorme. Parmi ce nombre d'automates, nous pouvons trouver un automate qui dessine n'importe quel modèle donné (avec une certaine précision pour les modèles plus complexes).

Le modèle suivant:



Dans les expériences précédentes, nous avons compté la somme des cellules autour desquelles un motif est formé (si avec une erreur, ajoutez 1 à la somme, si sans erreurs, ajoutez 2). La quantité résultante a été utilisée comme facteur de fitness pour l'algorithme génétique.

Pour un modèle plus complexe, cette méthode ne fonctionne pas. Un automate dans lequel un plus petit nombre de cellules correspond plus étroitement à un critère donné (le nombre de cellules correspondant à un motif au voisinage d'une cellule) perdra à chaque fois un automate dans lequel un plus grand nombre de cellules correspondra moins précisément à un critère donné. Comme dans l'exemple avec les carrés ci-dessus:



Pour le motif souhaité, à la 100e itération de chaque automate de la population, entouré de chaque cellule, nous considérerons le nombre de cellules correspondant au motif. Nous ne prendrons que le meilleur résultat pour chaque machine. Le nombre de cellules correspondant au motif sera utilisé comme facteur de fitness. Le motif se compose de 7x17 = 119 cellules. Ce nombre sera considéré comme la solution optimale. 6000 cycles d'évolution nous ont permis de trouver un automate qui dessine un motif avec 5 erreurs (114 cellules coïncident avec le motif).

Graphique sur une échelle arbitraire:



Une augmentation du pourcentage de mutations n'a pas altéré l'aptitude de la population.

Il existe de nombreux mutants dans le patrimoine génétique de la population:



Un automate aléatoire issu d'une population en dynamique:



La meilleure machine à la 100e itération:



Modèles recherchés et trouvés:



Ayant joué avec les critères de sélection, la taille du champ de l'automate et le pourcentage de mutations, il s'est avéré améliorer la population et trouver un automate qui ne fait que 3 erreurs dans le pattern.

Pool de gènes:



Machine à la 100e itération:



Modèles recherchés et trouvés:





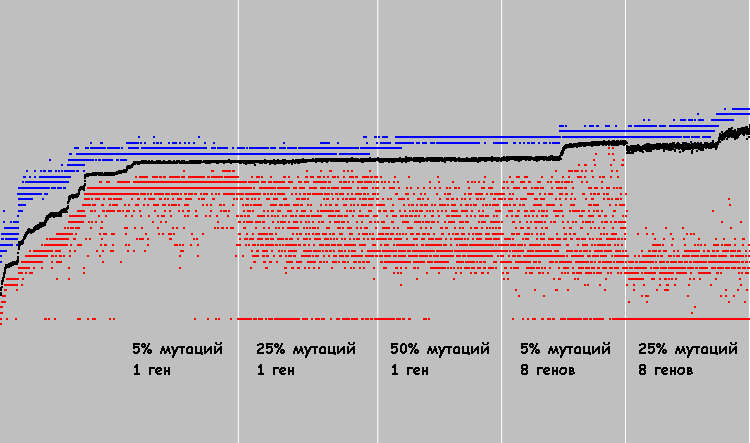
Dans quatre graphiques, vous pouvez voir comment le système évolue avec différentes probabilités de mutation (1 gène muté):



Les points rouges sont le coefficient de fitness moyen dans une population. Les points noirs représentent le coefficient de fitness de chaque individu. 3000 cycles d'évolution pour chaque système.

Pools de gènes de populations (dans le même ordre):









Automates à la 100e itération:









Faisons une autre expérience. Le schéma est le même. Les génotypes initiaux sont remplis de gènes aléatoires. La probabilité de mutations est de 5%. De 1 à 8 gènes mutent (un nombre aléatoire de gènes mutants est prélevé pour chaque individu). 100 cycles d'évolution.



Le graphique est une carte thermique. La taille des points sur le graphique est de 5 pixels. L'origine est le coin supérieur gauche.
Sur l'axe Y (de 0 à 100) - cycles d'évolution. Sur l'axe X (de 0 à 119) - le nombre de cellules coïncidant avec le motif (pour chaque individu de la population, nous obtenons le meilleur résultat). La luminosité du point est le nombre d'individus avec le résultat spécifié (coordonnée X).

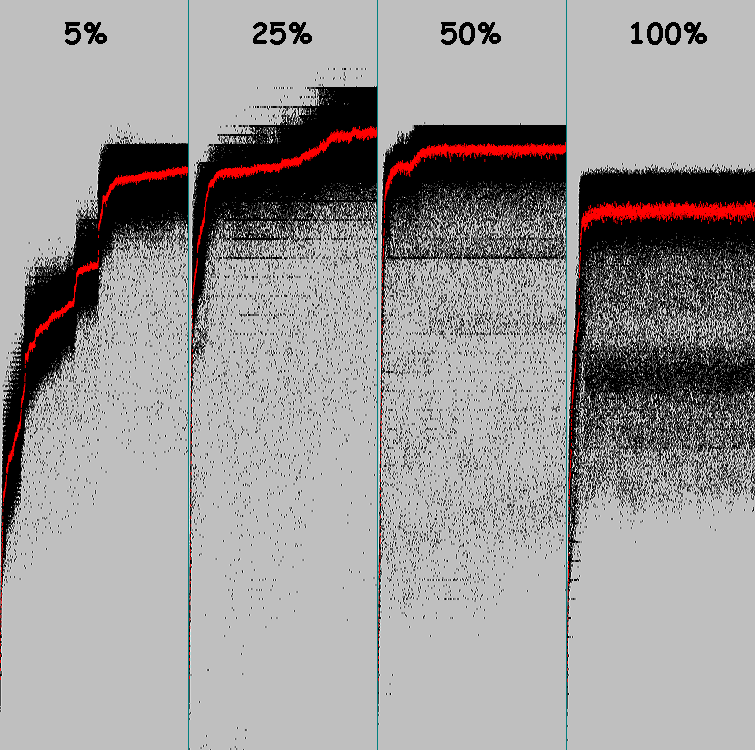
Exécutez l'algorithme génétique 4 fois avec les mêmes paramètres (100 cycles, 5% de mutations, jusqu'à 8 gènes mutent). Sur le graphique, les 5 départs:



Les 5 démarrages suivants: 25% de mutations, jusqu'à 8 gènes mutent:



L'échantillon est petit, mais nous pouvons tirer des conclusions sur l'efficacité de l'augmentation du pourcentage de mutations.

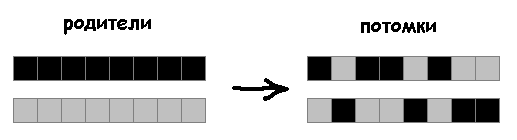
Ensuite, je montrerai l'inefficacité de la méthode de croisement utilisée dans l'article.

Méthode précédemment utilisée:



Au lieu de diviser le génotype en deux parties, les descendants hériteront de gènes ancestraux aléatoires:



5% de mutations:



25%:



Ensuite, nous utiliserons cette méthode de croisements.

Sur ce avec finition de sélection naturelle. Si quelqu'un a des idées intéressantes sur les critères de sélection naturelle, veuillez les exprimer dans les commentaires.

Pour la sélection artificielle, nous utiliserons des automates cellulaires de second ordre .

Automate cellulaire de second ordre

Considérons un automate cellulaire de dimension zéro du premier ordre (tous les automates cellulaires que nous avons considérés ci-dessus sont du premier ordre). Un automate cellulaire de dimension zéro se compose d'une cellule. Une cellule peut être dans l'un des deux états. L'état suivant de la cellule (t) est déterminé par l'état actuel de la cellule (t-1). Au total, il existe 4 automates cellulaires de dimension zéro (dont un oscillateur):



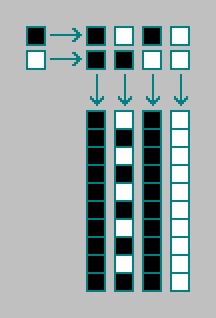
Dans un automate cellulaire du second ordre, l'état suivant de la cellule (t) est déterminé par l'état actuel (t-1) et l'état précédent de la cellule (t-2). Au total, il existe 4 combinaisons de deux états de cellule. $$ - le nombre d'automates cellulaires de dimension zéro du second ordre:



De tels automates cellulaires présentent des oscillateurs plus complexes.

$$ automates cellulaires du troisième ordre:



$$ les automates cellulaires de quatrième ordre ne peuvent pas être affichés sur une image.

Recherche d'automate cellulaire $$$n$ -e ordre avec une période d'oscillation égale à $$$n$ - La tâche est non triviale et extrêmement intéressante. Ce sujet mérite un article séparé.

Dans les automates cellulaires bidimensionnels unidimensionnels, l'état suivant d'une cellule est déterminé par l'état actuel de trois cellules et l'état précédent d'une cellule:



Il y a $$ automates cellulaires unidimensionnels du second ordre.

Code:



Les automates cellulaires de second ordre dessinent des motifs plus complexes que les automates cellulaires de premier ordre.

Dans les images ci-dessous, plusieurs machines aléatoires du deuxième ordre (sur le côté gauche de l'image - dans l'état t-1, une cellule est remplie, sur la droite - pour les états aléatoires t-1 et t-2, le code binaire est le contenu du tableau de règles):

0011111011001000:


0101101110010011110:


0110000110010010:


0110011010010110:


1110011010010110:


0110111010000101:


1111101001110110:


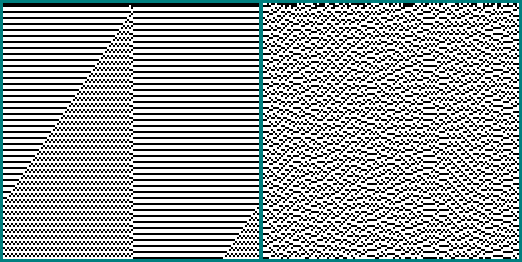1001010001100000:


la même machine 256x256:



512x512



D'autres machines peuvent être vues ici:
Machine cellulaire unidimensionnelle de deuxième ordre.
Automate cellulaire unidimensionnel du troisième ordre.

Les automates cellulaires unidimensionnels de second ordre se trouvent dans le livre de Wolfram, A New Kind of Science.

Sélection artificielle

Comme un automate cellulaire unidimensionnel du deuxième ordre, dans un automate cellulaire bidimensionnel du deuxième ordre, nous utiliserons une cellule supplémentaire de l'état précédent (t-2) de l'automate.

Pour plus de commodité, nous plaçons cette cellule au début de la ligne binaire: la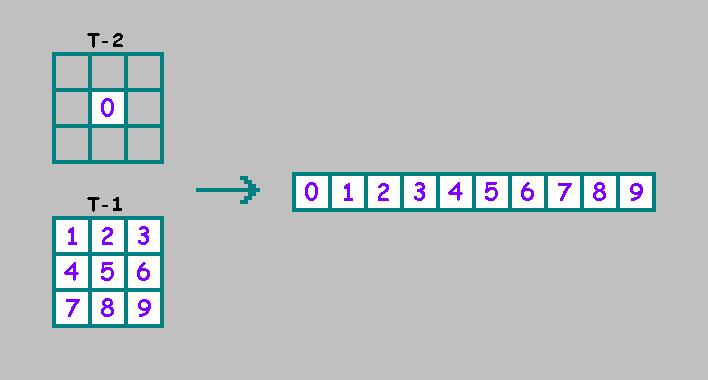



commodité réside dans le fait que lorsque la première et la seconde moitié du génotype coïncident, l'automate peut être considéré comme un automate de premier ordre:



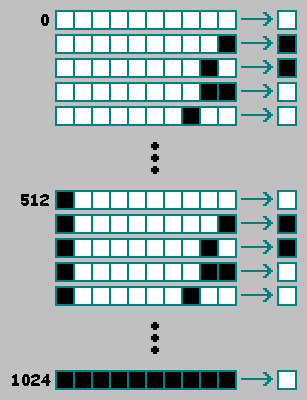en ajoutant une cellule, nous avons augmenté le nombre d'automates existants dans$$2 512 fois.$2^{512}$
$$2 512 × 2 512 = 2 1024 - le nombre d'automates bidimensionnels existants du deuxième ordre. Pour la sélection naturelle, nous avons déterminé un critère et comparé les automates par ce critère. Dans le processus de sélection artificielle, nous sélectionnons les machines manuellement, en utilisant un principe indistinct: "cette machine est intéressante, mais ce n'est pas très." Ce principe ne vous permet pas de choisir la meilleure machine parmi les machines aléatoires:Il existe plusieurs façons de résoudre ce problème. Je propose d'envisager quatre voies.$2^{512} \times 2^{512} = 2^{1024}$

1. Dans l'état initial de la machine, une cellule est remplie

Une façon consiste à observer le développement d'un automate cellulaire, dans l'état initial duquel une cellule est remplie.

Nous remplissons la population initiale avec des machines aléatoires. Plusieurs machines de la population initiale (30 itérations pour chacune):





Un petit nombre d'automates présentant un comportement moins chaotique sont présents dans la population. Nous les sélectionnerons pour le croisement:





20 machines aléatoires de la population initiale (état des machines à la 30ème itération):



Après trois cycles d'évolution:



Après huit cycles d'évolution:



Huit cycles d'évolution ont suffi pour remplir toute la population d'une machine avec un certain trait (une machine qui dessine des triangles) .

2. Le génotype est partiellement rempli

Si le rapport des unités et des zéros dans le génotype est violé, le rapport des unités et des zéros dans le phénotype est violé.

Dans le génotype (règle) de l'automate, les conditions cellulaires suivantes sont enregistrées pour toutes les combinaisons possibles de la cellule et des cellules voisines. S'il y a plus de zéros (ou de uns) dans le génotype, alors les zéros (ou les uns) s'accumulent dans les états suivants de l'automate. Il est intéressant de regarder la corrélation entre le rapport des uns et des zéros dans le génotype et le rapport des uns et des zéros dans le phénotype.

Construisez un graphique.

Créez une population de 200 machines. Nous remplissons les génotypes de zéros (1024 gènes dans le génotype d'un automate bidimensionnel de second ordre). Suivant $$n gènes sont remplis d'unités. Pour la première population$n$$$n = 0 , pour la 513e population$n=0$$$$n=512$ . Le long de l'axe $$x est le nombre d'habitants. Le long de l'axe$x$$$y marque (avec des points blancs) le rapport des uns et des zéros dans le pool génétique de la population. Nous avons une hyperbole:pour chaque automate (avec une taille de champ de 89x89), nous considérons 100 itérations. À la 100e itération, nous comptons le nombre de uns et de zéros dans l'état (phénotype) de chaque automate. Nous marquons sur le graphique le rapport des unités et des zéros (le nombre total de toutes les unités est divisé par le nombre total de tous les zéros). Nous avons une courbe: aulieu du rapport total des uns et des zéros dans tous les phénotypes, vous pouvez regarder le rapport des uns et des zéros dans chaque phénotype:Sur le côté gauche du graphique, il y a des points avec la plus grande déviation de la valeur moyenne. On peut supposer qu'il s'agit d'automates dans les génotypes dont le gène zéro est égal à l'unité. Supposé - vérifié. Nous mettons le gène zéro toujours égal à zéro. 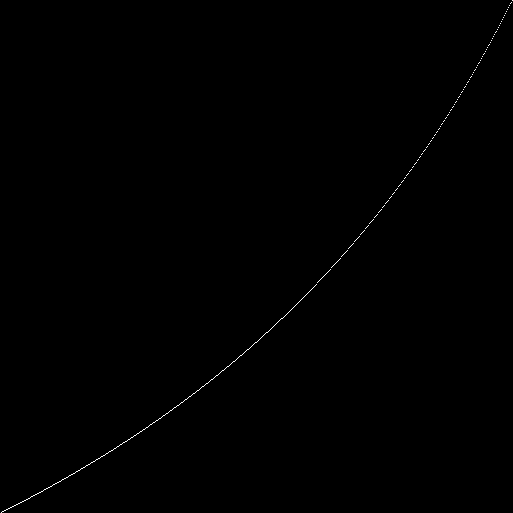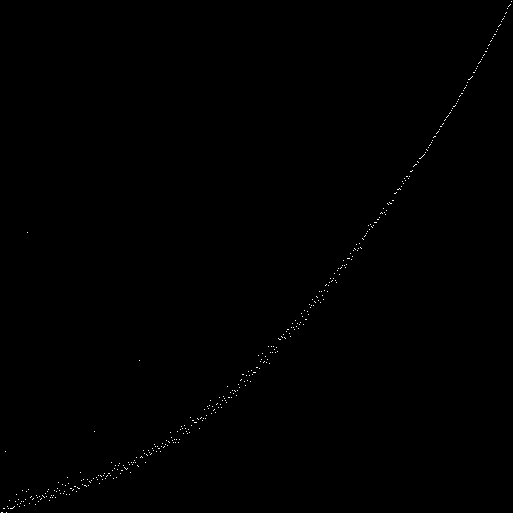Nous dessinons un nouveau graphique:$y$















Comparez avec les machines dans lesquelles le gène zéro est toujours égal à un:



dans les machines du second ordre, il existe un autre gène «zéro» - le 512e. Voyons comment ce gène affecte le phénotype.

Les 0e et 512e gènes sont toujours nuls: le



0e gène est toujours nul. Le 512ème gène est toujours égal à un:



Afin de ne pas se moquer à nouveau de nos estimés épileptiques, le 0ème et le 512ème gène seront remplis de zéros dans la population initiale de l'algorithme génétique.

Examinons les machines dont nous nous sommes débarrassés en définissant des zéros sur les gènes 0e et 512e.

Les 8 premiers états d'un automate dans lequel seul le 0ème gène est rempli (le gène zéro est un, les autres sont des zéros): Un



automate dans lequel seul le 512ème gène



est rempli : Un automate dans lequel seuls les 0ème et 512ème gènes sont remplis:



Choisissons un endroit sur le graphique où la population commence à se diviser en groupes: à



cet endroit, les génotypes sont remplis à 25%.

Comparez deux populations.

Première population. 30 machines aléatoires sur la 1000e itération. Les génotypes sont pleins à 50% (512 unités et 512 zéros):



la deuxième population. 30 machines aléatoires sur la 1000e itération. Les génotypes sont remplis à 25% (256 unités et 768 zéros):



la deuxième population est adaptée à la sélection artificielle. Nous pouvons facilement mettre en évidence certains des signes de ces machines. Par exemple: «plus sombre», «moins chaotique» (automates dans lesquels les globules blancs sont regroupés), etc.

Nous sélectionnons "plus sombre". La probabilité de mutations est de 10%, jusqu'à 4 gènes mutent. Après la première sélection:



Après la deuxième sélection:



Un automate intéressant est apparu dans la population.

256x256, état de la machine à la 1000ème itération: La



machine remplit progressivement la population.

Après la huitième sélection:



Une autre machine intéressante est apparue.

256x256, état de l'automate à la 1000e itération:



Population après treize sélections:



Plusieurs automates de cette population. 256x256, 1000e itération pour tout le monde. Sous l'image est un lien, en cliquant sur lequel, vous pouvez regarder la machine dans la dynamique:


Voir en dynamique.


Voir en dynamique.


Voir en dynamique.


Voir en dynamique.


Voir en dynamique.


Voir en dynamique.


Voir en dynamique.


Voir en dynamique.


Voir en dynamique.


Voir en dynamique.

3. Machine automatique Conway et similaires

L'automate cellulaire bidimensionnel le plus célèbre du premier ordre est le jeu d' automates Conway «Life» .

Les règles de l'automate Conway sont écrites comme suit:
s'il y a 3 cellules vivantes autour d'une cellule morte, la cellule prend vie (sinon elle reste morte).
S'il y a 2 ou 3 cellules vivantes autour d'une cellule vivante, la cellule reste vivante (sinon elle meurt).
Une cellule morte est 0, une cellule vivante est 1.

Autour d'une cellule peut être de 0 à 8 cellules vivantes. Selon 9 options autour du vivant et de la cellule morte. Nous écrivons toutes les options dans le tableau r:



La première moitié du tableau est pour une cellule morte, la seconde pour une cellule vivante.

Nous pouvons décrire la règle de l'automate Conway pour toutes les combinaisons (512) possibles d'une cellule et de 8 cellules voisines:





Pour un automate de second ordre, copiez la seconde moitié du tableau de règles à partir du premier:



Nous démarrons la machine avec la règle spécifiée. On voit les planeurs et oscillateurs caractéristiques. Plusieurs itérations de cet automate:



Array r se compose de 18 cellules. Il y a$$2 18 = 262144 automates similaires à l'automate Conway (qui peut s'écrire selon les mêmes règles: le nombre de cellules vivantes entourées de morts, dans lesquelles la cellule prend vie et le nombre de cellules vivantes dans le milieu vivant, dans lequel la cellule meurt).Vous pouvez les regarderici(par défaut, l'automate Conway démarre, le bouton «Changer la règle» remplit le tableau r de façon aléatoire).Plusieurs machines aléatoires (code binaire - tableau r):110010011001111111100001100110111110011111000100101110010000110000110010001111010011100111000111001000000110000101100010100001000001111101011111000001100110111111$2^{18}=262144$































Pour un algorithme génétique, en tant que génotype, vous pouvez utiliser, comme un tableau r ( $$2 18 combinaisons) et le tableau de règles ($2^{18}$$$2 512 combinaisons de premier ordre pour l'automate cellulaire et$2^{512}$$$2 1024 - pour un automate cellulaire du second ordre).$2^{1024}$

$$2 18 est un nombre relativement petit. Ce nombre vous permet de sélectionner la règle pour la machine manuellement, sans utiliser d'algorithme génétique (en fait, ce que Conway a fait). Si vous remplissez le tableau de règles avec des machines aléatoires de ce type et utilisez ce tableau comme génotype, l'expérience peut être considérée comme infructueuse, dans une certaine mesure (suffisamment pour ne pas afficher les résultats de cette expérience dans l'article). Dans les règles des automates cellulaires de ce type, il y a symétrie. Par exemple, pour les combinaisons de cellules suivantes:$2^{18}$






l'état de la cellule à la prochaine itération est le même. Après le premier croisement, la symétrie dans les règles des individus descendants est rompue. Les individus ancestraux accumulent des mutations qui détruisent également la symétrie. La violation de la symétrie dans le génotype provoque une violation de la symétrie dans le phénotype.

On peut voir la manifestation de cette symétrie dans le phénotype si une cellule est remplie dans l'état initial de l'automate.

Faisons une expérience. Pour maintenir la symétrie, nous utiliserons le tableau r comme génotype. 5% de mutations, 1 gène muté. Dans l'état initial, une cellule est remplie.

30 machines aléatoires de la population initiale. L'état des automates à la 30e itération:



Essayons d'isoler les automates qui se développent (se développent) le plus lentement à partir d'une cellule.







Après la première sélection, ils se sont débarrassés des automates qui ne se développent pas:



dans la nouvelle population, il y a plusieurs automates de ce type (qui ne se développent pas) - ce sont des descendants et des mutants infructueux.

Ensuite, nous sélectionnerons principalement des machines à fond blanc (cellules sur lesquelles la machine n'a pas évolué).


Population après la deuxième sélection:



3 sélections:



5 sélections:



8 sélections:



13 sélections:



Les mêmes machines à la 60e itération:



21 sélections. L'état des automates à la 30e itération: L'



état des automates à la 60e itération:



34 sélections. État des automates à la 30e itération:



État des automates à la 60e itération:



De plus, le système n'évolue pas. Trois automates de cette population (100 itérations

chacun ): [1,0,1,1,1,0,0,1,0,0,1,1,0,1,0,1,1,1]


[1 , 0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,1,1]


[1,0,0,1,1,0,0, 1,1,0,1,0,1,1,0,1,1,1]


A titre de comparaison, une machine aléatoire:

[1,0,0,1,1,1,0,1,1,1,0, 0,1,1,0,0,0,1]

4. Automate Conway et similaires (2)

Dans les machines avec les règles de type Conway, on compte le nombre de cellules (unités) vivantes à proximité de Moore. Ce voisinage peut être divisé en 4 paires et compter le nombre de cellules vivantes dans ces paires: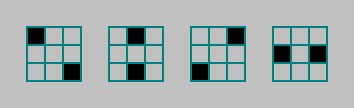



Ainsi, nous augmentons le nombre d'automates, mais maintenons la symétrie dans le phénotype.

Chaque paire peut avoir de 0 à 2 cellules vivantes. Par 4. Nombre de combinaisons$$$3^4=81$ .Selon la 81e combinaison autour du vivant et de la cellule morte. Le total existe$$2 162 machines automatiques de ce type. Numéro:$2^{162}$

$$

$$2^{162}\approx5.846\times10^{48}$$

Il est complètement astronomique et conviendra à un algorithme génétique.

La taille du génotype de chaque individu est de 162 gènes:


Ensuite, nous peignons cette règle pour toutes les combinaisons possibles d'une cellule et de huit cellules voisines:


Nous utiliserons le tableau de règles lors du calcul de l'état suivant de l'automate. Nous appelons la fonction fillrule () après avoir chargé la page et après avoir appelé la fonction evolute ().

La population initiale semble chaotique. 30 machines aléatoires, 1000e itération:



Ce chaos varie légèrement en dynamique et les machines sont tout à fait adaptées à la sélection, mais facilitons les choses - nous choisirons les plus «sombres».

Population après cinq sélections:



Ensuite, vous pouvez rechercher des machines avec les oscillateurs les plus complexes. L'ensemble du processus de mise en page est inutile. Voici quelques-uns des automates les plus intéressants trouvés en utilisant l'algorithme génétique.

256x256, 10000e itération pour tout le monde. Sous l'image est un lien, en cliquant sur lequel, vous pouvez regarder la machine dans la dynamique:


Voir en dynamique.


.


.


.


.


.


.


.


.


.


.


.


.


.

?

Et vous pouvez jouer ici:

des automates cellulaires bidimensionnels du deuxième ordre.

Interface: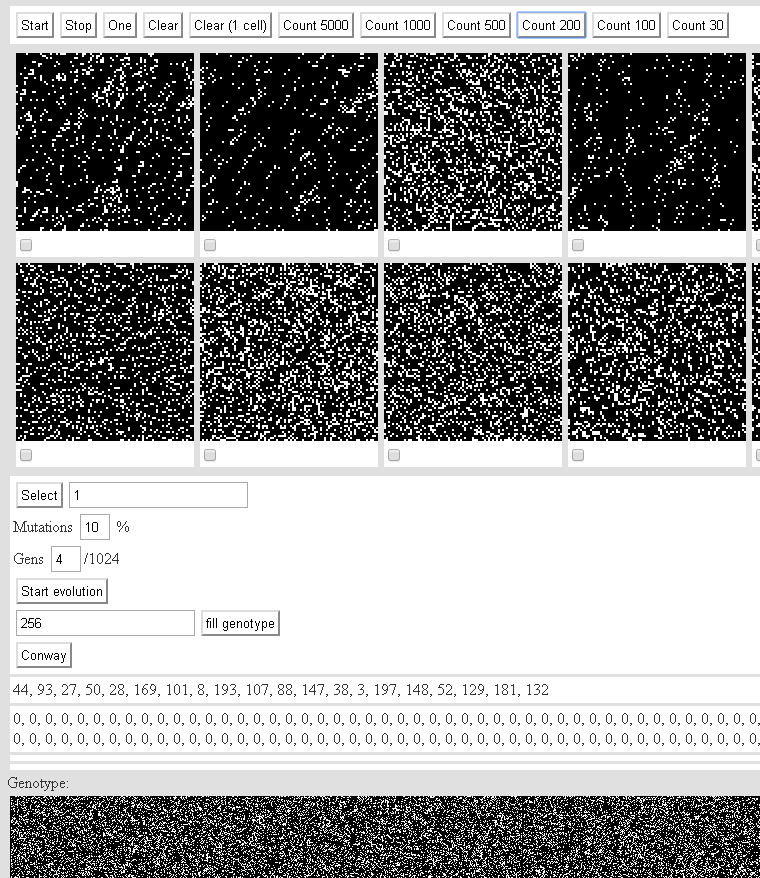



Le bouton Démarrer démarre les machines.
Stop - s'arrête.
L'un est une itération.
Clear - arrête la machine et remplit l'état initial avec un hasard.
Effacer (1 cellule) - arrête la machine et remplit une cellule dans l'état initial.
Les boutons restants sur cette ligne comptent le nombre d'itérations spécifié pour chaque automate.
Le rendu d'un automate sur toile dévore toutes les performances. Si vous avez besoin de calculer rapidement 200 itérations - cliquez sur Count 200. Nous ne cliquons pas sur le bouton Count 5000 - le navigateur peut le bloquer.

Moins de 20 machines aléatoires (taille de la population - 200 machines). Sous les cases à cocher des distributeurs automatiques. Nous marquons le plus intéressant. Appuyez sur Sélectionner - la condition physique de la machine augmentera du nombre indiqué à droite.
Mutations - la probabilité de mutations.
Gens est le nombre de gènes mutants.

Commencer l'évolution - lance le mécanisme des croisements et des mutations.

Remplir le génotype - remplit le nombre spécifié de gènes dans le génotype de chaque automate.
Conway - remplit la population avec des machines de type Konveevsky.

Ci-dessous, deux lignes: Les
numéros des machines affichées.
Le contenu du tableau de fenotype.

Le patrimoine génétique de la population est encore plus faible.

Toute progression est stockée dans le stockage local.

Vous pouvez jouer avec des fusils d'assaut de type Konveevsky (avec ceux qui étaient considérés en dernier dans l'article) ici:

4. Automate Conway et similaires (2).