Comment résoudre les problèmes NP-hard en utilisant des algorithmes paramétrés

Le travail de recherche est peut-être la partie la plus intéressante de notre formation. L'idée est de vous essayer dans la direction choisie même à l'université. Par exemple, les étudiants des domaines du génie logiciel et de l'apprentissage automatique vont souvent faire des recherches dans l'entreprise (principalement JetBrains ou Yandex, mais pas seulement).

Dans cet article, je parlerai de mon projet en informatique. Dans le cadre du travail, j'ai étudié et mis en pratique des approches pour résoudre l'un des problèmes NP-durs les plus connus: le problème de la couverture des sommets .

Désormais, une approche intéressante des problèmes difficiles liés au NP se développe rapidement - des algorithmes paramétrés. Je vais essayer de vous mettre au courant, de vous présenter quelques algorithmes paramétrés simples et de décrire une méthode puissante qui m'a beaucoup aidé. J'ai présenté mes résultats au PACE Challenge: selon les résultats des tests ouverts, ma décision est en troisième position, et les résultats définitifs seront connus le 1er juillet.

À propos de moi

Je m'appelle Vasily Alferov, je termine maintenant la troisième année de HSE - Saint-Pétersbourg. J'adore les algorithmes depuis la rentrée, lorsque j'ai étudié à l'école 179 de Moscou et participé avec succès à des concours d'informatique.

Le dernier nombre de spécialistes des algorithmes paramétrés passe à la barre ...

Un exemple est tiré du livre "Algorithmes paramétrisés"

Imaginez que vous êtes gardien de bar dans une petite ville. Tous les vendredis, la moitié de la ville vient dans votre bar pour se détendre, ce qui vous donne beaucoup de mal: vous devez chasser les visiteurs violents du bar pour éviter les combats. Au final, cela vous dérange et vous décidez de prendre des mesures préventives.

Étant donné que votre ville est petite, vous savez avec certitude quelles paires de visiteurs sont très susceptibles de se disputer si elles arrivent au bar ensemble. Vous avez une liste de n personnes qui viendront au bar ce soir. Vous décidez de ne laisser aucun citadin dans le bar pour que personne ne se bat. Dans le même temps, vos supérieurs ne veulent pas perdre de bénéfices et seront mécontents si vous ne laissez pas plus de k personnes aller au bar.

Malheureusement, le défi auquel vous êtes confronté est une tâche classique difficile pour NP. Vous pouvez le connaître sous le nom de couverture de sommet ou comme problème de couverture de sommet. Pour de tels problèmes, dans le cas général, les algorithmes qui fonctionnent dans un temps acceptable sont inconnus. Pour être précis, l'hypothèse non prouvée et assez forte ETH (Exponential Time Hypothesis) dit que ce problème ne peut pas être résolu dans le temps $$$2 ^ {o (n)}$c'est-à-dire que ce qui est sensiblement meilleur qu'une recherche exhaustive ne peut être pensé. Par exemple, laissez n = 1000 personnes prévoir de venir dans votre bar. Ensuite, une recherche complète sera $$$2 ^ {1000}$les options qu'il y a à peu près $$ - incroyablement. Heureusement, votre guide vous a fixé une limite k = 10 , donc le nombre de combinaisons dont vous avez besoin pour itérer est beaucoup moins: le nombre de sous-ensembles de dix éléments est $$ . C'est déjà mieux, mais ne compte toujours pas pour la journée, même sur un cluster puissant.

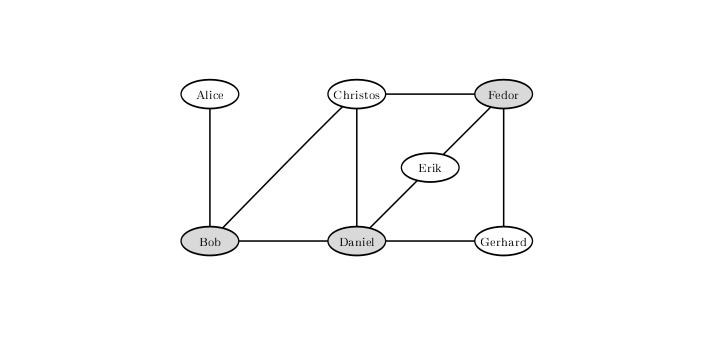
Pour exclure la possibilité d'un combat avec une telle configuration de relations tendues entre les visiteurs du bar, vous ne devez pas laisser Bob, Daniel et Fedor. Il n'existe pas de solution dans laquelle il n'en reste que deux par dessus bord.

Est-ce à dire qu'il est temps de se rendre et de laisser entrer tout le monde? Examinons d'autres options. Eh bien, par exemple, vous ne pouvez pas laisser entrer uniquement ceux qui sont susceptibles de se battre avec un très grand nombre de personnes. Si quelqu'un peut se battre avec au moins k + 1 par une autre personne, alors vous ne pouvez certainement pas le laisser entrer, sinon vous devrez ne pas laisser tous les citadins k + 1 avec lesquels il peut se battre, ce qui bouleversera certainement le leadership.

Puissiez-vous jeter tout ce que vous pourriez selon ce principe. Ensuite, tout le monde peut se battre avec pas plus de k personnes. Jeter k personnes, vous ne pouvez empêcher que $$$k ^ 2$conflits. Donc, si tout cela dépasse $$ si une personne est impliquée dans au moins un conflit, vous ne pouvez certainement pas tous les empêcher. Puisque, bien sûr, vous êtes sûr de laisser partir complètement les personnes non conflictuelles, vous devez alors trier tous les sous-ensembles de la taille de dix personnes sur deux cents. Il y a environ $$ , et de nombreuses opérations peuvent déjà être triées sur le cluster.

S'il est sûr de prendre des personnalités totalement non conflictuelles, qu'en est-il de ceux qui sont impliqués dans un seul conflit? En fait, ils peuvent aussi être laissés entrer en fermant les portes devant leur adversaire. En effet, si Alice entre en conflit uniquement avec Bob, alors si nous laissons entrer deux d'entre eux, Alice, nous ne perdrons pas: Bob peut avoir d'autres conflits, mais Alice n'en a certainement pas. De plus, cela n'a aucun sens pour nous de ne pas laisser les deux. Après de telles opérations, plus $$$k ^ 2$invités avec un sort non résolu: tout ce que nous avons $$$k ^ 2$conflits, dans chacun des deux participants et chacun impliqué dans au moins deux. Donc, il ne reste plus qu'à trier $$ options, qui peuvent bien être calculées pour une demi-journée sur un ordinateur portable.

En fait, un simple raisonnement peut créer des conditions encore plus attrayantes. Notez que nous devons absolument résoudre tous les différends, c'est-à-dire de chaque paire en conflit pour choisir au moins une personne que nous ne laisserons pas entrer. Considérez cet algorithme: prenez tout conflit dont nous supprimons un participant et commençons récursivement à partir du reste, puis supprimez un autre et démarrez également récursivement. Puisque nous jetons quelqu'un à chaque étape, l'arbre de récursivité d'un tel algorithme est un arbre binaire de profondeur k , donc, au total, l'algorithme fonctionne pour $$$2 ^ k⋅ (n + m)$où n est le nombre de sommets et m est le nombre d'arêtes. Dans notre exemple, c'est environ dix millions, qui en une fraction de seconde seront comptés non seulement sur un ordinateur portable, mais même sur un téléphone mobile.

L'exemple ci-dessus est un exemple d' algorithme paramétré . Les algorithmes paramétrés sont des algorithmes qui fonctionnent pendant f (k) poly (n) , où p est un polynôme, f est une fonction arbitraire calculable et k est un paramètre qui, très probablement, sera beaucoup plus petit que la taille du problème.

Toutes les discussions antérieures à cet algorithme donnent un exemple de noyauisation , l'une des techniques courantes de création d'algorithmes paramétrés. La noyauisation est une réduction de la taille d'une tâche à une valeur limitée par une fonction d'un paramètre. La tâche résultante est souvent appelée noyau. Ainsi, par un simple raisonnement sur les degrés de sommets, nous avons obtenu un noyau quadratique pour le problème de Vertex Cover, paramétré par la taille de la réponse. Il existe d'autres paramètres qui peuvent être sélectionnés pour cette tâche (par exemple, Vertex Cover Above LP), mais nous allons discuter d'un tel paramètre.

Défi d'allure

Le concours PACE Challenge (The Parameterized Algorithms and Computational Experiments) a débuté en 2015 pour établir un lien entre les algorithmes paramétrés et les approches utilisées dans la pratique pour résoudre les problèmes de calcul. Les trois premiers concours ont été consacrés à trouver la largeur d'arbre du graphique ( Treewidth ), à trouver l' arbre Steiner ( arbre Steiner ) et à trouver de nombreux sommets, cycles de coupe ( Feedback Vertex Set ). Cette année, l'une des tâches dans lesquelles on pouvait essayer ses forces était le problème de la couverture supérieure décrit ci-dessus.

La concurrence gagne en popularité chaque année. Si vous croyez aux données préliminaires, cette année, seules 24 équipes ont participé au concours pour résoudre le problème de la couverture des sommets. Il est à noter que la compétition ne dure pas plusieurs heures, ni même une semaine, mais plusieurs mois. Les équipes ont la possibilité d'étudier la littérature, de proposer leur idée originale et d'essayer de la mettre en œuvre. En fait, ce concours est un travail de recherche. Des idées pour les solutions les plus efficaces et l'attribution des gagnants seront organisées conjointement avec la conférence IPEC (International Symposium on Parameterized and Exact Computation) lors de la plus grande réunion algorithmique annuelle en Europe ALGO . Vous trouverez plus d'informations sur le concours lui-même sur le site Internet et les résultats des dernières années sont ici .

Schéma de solution

Pour faire face au problème de la couverture des sommets, j'ai essayé d'appliquer des algorithmes paramétrés. Ils se composent généralement de deux parties: les règles de simplification (qui conduisent idéalement à la nucléation) et les règles de fractionnement. Les règles de simplification sont le prétraitement des entrées en temps polynomial. Le but de l'application de telles règles est de réduire le problème à un problème équivalent de plus petite taille. Les règles de simplification sont la partie la plus chère de l'algorithme, et l'application de cette partie particulière conduit à la durée totale du travail $$$c ^ k⋅poly (n)$au lieu du simple temps polynomial. Dans notre cas, les règles de fractionnement sont basées sur le fait que pour chaque sommet, vous devez prendre soit son voisin en réponse.

Le schéma général est le suivant: nous appliquons les règles de simplification, puis sélectionnons un sommet et faisons deux appels récursifs: dans le premier, nous le prenons en réponse, et dans l'autre, nous prenons tous ses voisins. C'est ce que nous appelons le fractionnement (brunch) le long de ce pic.

Un ajout exact sera apporté à ce schéma dans le paragraphe suivant.

Idées pour diviser les règles

Voyons comment choisir un sommet le long duquel le fractionnement se produira.
L'idée principale est très gourmande au sens algorithmique: prenons le pic du degré maximum et divisons-le par lui. Pourquoi cela semble-t-il si meilleur? Parce que dans la deuxième branche de l'appel récursif, nous allons supprimer autant de sommets de cette manière. Vous pouvez vous attendre à ce qu'un petit graphique reste et nous y travaillerons rapidement.

Cette approche, avec les techniques simples de kernelization déjà discutées, n'est pas mauvaise, elle résout certains tests avec une taille de plusieurs milliers de sommets. Mais, par exemple, cela ne fonctionne pas bien pour les graphiques cubiques (c'est-à-dire les graphiques dont le degré de chaque sommet est de trois).
Il existe une autre idée basée sur une idée assez simple: si le graphique est déconnecté, le problème sur ses composants connectés peut être résolu indépendamment en combinant les réponses à la fin. C'est d'ailleurs la petite modification promise du schéma, qui accélérera considérablement la solution: auparavant, dans ce cas, nous avons travaillé pour le produit des temps de comptage des réponses des composants, et maintenant nous travaillons pour le montant. Et pour accélérer le brunch, vous devez transformer un graphique connecté en graphique déconnecté.

Comment faire S'il y a un point d'articulation dans le graphique, il faut le parcourir. Un point d'articulation est un sommet tel que, lorsqu'il est supprimé, le graphique perd sa connectivité. Trouver dans le graphique tous les points du joint peuvent être un algorithme classique en temps linéaire. Cette approche accélère considérablement le brunch.

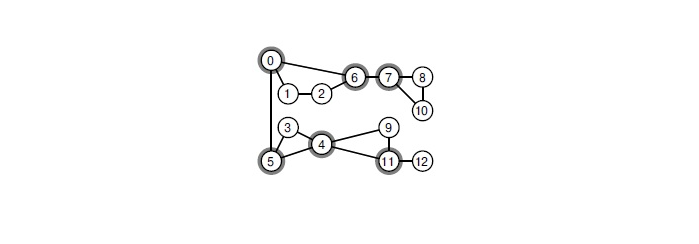
Lorsque vous supprimez l'un des sommets sélectionnés, le graphique se décompose en composants connectés.

Nous le ferons, mais j'en veux plus. Par exemple, recherchez les petites sections de sommets dans le graphique et séparez-les le long des sommets. Le moyen le plus efficace que je connaisse pour trouver la section minimale du sommet global est d'utiliser l'arbre Gomori-Hu, qui est construit en temps cubique. Dans le défi PACE, une taille de graphique typique est de plusieurs milliers de sommets. Dans ce scénario, des milliards d'opérations doivent être effectuées à chaque sommet de l'arbre de récursivité. Il s'avère qu'il est tout simplement impossible de résoudre le problème dans le délai imparti.

Essayons d'optimiser la solution. La section de sommet minimum entre une paire de sommets peut être trouvée par n'importe quel algorithme construisant le flux maximum. Vous pouvez exécuter l' algorithme Dinitz sur un tel réseau; en pratique, cela fonctionne très rapidement. Je soupçonne qu'il est théoriquement possible de prouver une estimation du temps de travail $$$mn ^ {1/2}$c'est déjà tout à fait acceptable.

J'ai essayé plusieurs fois de rechercher des coupes entre des paires de sommets aléatoires et d'en prendre la plus équilibrée. Malheureusement, dans les tests ouverts du Challenge PACE, cela a donné de mauvais résultats. Je l'ai comparé à un algorithme dispersé le long des sommets du degré maximum, en les commençant par une restriction sur la profondeur de descente. Après que l'algorithme ait essayé de trouver la coupe de cette manière, il restait des graphiques plus grands. Cela est dû au fait que les coupes se sont révélées très déséquilibrées: après la suppression de 5 à 10 pics, seuls 15 à 20 ont pu être séparés.

Il convient de noter que les articles sur les algorithmes théoriquement les plus rapides utilisent des techniques beaucoup plus avancées pour sélectionner les sommets à fractionner. De telles techniques ont une implémentation très complexe et souvent de faibles niveaux de temps et de mémoire. Je ne pouvais pas en distinguer tout à fait acceptable pour la pratique.

Comment appliquer les règles de simplification

Nous avons déjà des idées de noyauisation. Permettez-moi de vous rappeler:

1. S'il existe un sommet isolé, supprimez-le.
2. S'il existe un sommet de degré 1, supprimez-le et prenez son voisin en réponse.
3. S'il existe un sommet de degré au moins k + 1 , prenez-le en réponse.

Avec les deux premiers, tout est clair, avec le troisième, il y a un truc. Si dans le problème de la bande dessinée, on nous a donné une restriction d'en haut sur k , alors dans le défi PACE, il vous suffit de trouver la couverture de sommet de la taille minimale. Il s'agit d'une transformation typique d'un problème de recherche en problème de décision, souvent entre les deux types de tâches, ils ne font pas de différence. En pratique, si nous écrivons un résolveur de problèmes de couverture de sommets, il peut y avoir une différence. Par exemple, comme dans le troisième paragraphe.

En termes de mise en œuvre, il existe deux façons de procéder. La première approche est appelée approfondissement itératif. Il consiste en ce qui suit: nous pouvons commencer avec une restriction raisonnable d'en bas sur la réponse, puis exécuter notre algorithme, en utilisant cette restriction comme une restriction sur la réponse d'en haut, sans descendre en récursivité plus bas que cette restriction. Si nous trouvons une réponse, elle est garantie d'être optimale, sinon vous pouvez augmenter cette limite d'une unité et recommencer.

Une autre approche consiste à stocker une réponse optimale actuelle et à rechercher une réponse plus petite, lorsqu'elle est trouvée, modifiez ce paramètre k pour couper davantage les branches en excès dans la recherche.

Après avoir fait des expériences nocturnes, j'ai opté pour une combinaison de ces deux méthodes: d'abord, je lance mon algorithme avec une sorte de restriction sur la profondeur de recherche (en le choisissant pour qu'il prenne un temps insignifiant par rapport à la solution principale) et j'utilise la meilleure solution trouvée comme une restriction d'en haut à la réponse - c'est-à-dire à ce très k .

Sommets de degré 2

Avec des sommets de degrés 0 et 1, nous avons compris. Il s'avère que cela peut également être fait avec des sommets de degré 2, mais pour cela, le graphique nécessitera des opérations plus complexes.

Pour expliquer cela, vous devez en quelque sorte identifier les pics. Nous appelons un sommet de degré 2 le sommet v , et ses voisins les sommets x et y . Ensuite, nous aurons deux cas.

1. Lorsque x et y sont voisins. Ensuite, vous pouvez prendre les réponses x et y et supprimer v . En effet, à partir de ce triangle, au moins deux sommets doivent être pris en réponse et nous ne perdrons certainement pas si nous prenons x et y : ils ont probablement plus de voisins, et v non.
2. Lorsque x et y ne sont pas voisins. Ensuite, il est indiqué que les trois sommets peuvent être collés ensemble en un seul. L'idée est que dans ce cas, il existe une réponse optimale dans laquelle nous prenons soit v soit les deux sommets x et y . De plus, dans le premier cas nous devons prendre en réponse tous les voisins x et y , et dans le second ce n'est pas nécessaire. C'est exactement le cas quand on ne prend pas le sommet collé en réponse et quand on le prend. Reste à noter que dans les deux cas la réponse d'une telle opération diminue d'une unité.

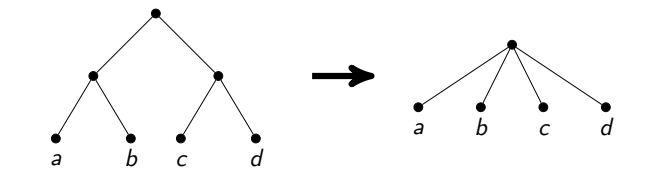
Il convient de noter qu'une telle approche pour un temps linéaire honnête est assez difficile à mettre en œuvre avec précision. Le collage des sommets est une opération difficile, vous devez copier les listes de voisins. Si vous faites cela négligemment, vous pouvez obtenir un temps de fonctionnement asymptotiquement non optimal (par exemple, si vous copiez beaucoup de bords après chaque collage). J'ai décidé de rechercher des chemins entiers à partir de sommets de degré 2 et d'analyser un tas de cas spéciaux, tels que les boucles de ces sommets ou de tous ces sommets sauf un.

De plus, il est nécessaire que cette opération soit réversible, afin que lors du retour de récursivité nous restituions le graphe dans sa forme d'origine. Pour cela, je n'ai pas effacé les listes d'arêtes des sommets fusionnés, après quoi je savais juste vers quelles arêtes il fallait diriger. Cette implémentation de graphiques nécessite également de la précision, mais elle fournit un temps linéaire honnête. Et pour les graphiques de plusieurs dizaines de milliers d'arêtes, il s'intègre complètement dans le cache du processeur, ce qui offre de grands avantages de vitesse.

Noyau linéaire

Enfin, la partie la plus intéressante du noyau.

Tout d'abord, rappelons que dans les graphes bipartis, la couverture minimale des sommets peut être recherchée pour $$$mn ^ {1/2}$. Pour ce faire, utilisez l'algorithme Hopcroft-Karp pour y trouver la correspondance maximale, puis utilisez le théorème de Koenig-Egerwari .

L'idée d'un noyau linéaire est la suivante: on divise d'abord le graphe, c'est-à-dire qu'au lieu de chaque sommet v, on obtient deux sommets $$$v_L$et $$$v_R$, et au lieu de chaque bord u - v, nous avons deux bords $$$u_L - v_R$et $$$v_L - u_R$. Le graphique résultant sera bipartite. On y retrouve la couverture minimale des sommets. Certains sommets du graphique d'origine y arrivent deux fois, certains une seule fois et d'autres jamais. Le théorème de Nemhauser-Trotter déclare que dans ce cas, il est possible de supprimer les sommets qui n'ont pas été touchés une fois et de répondre à ceux qui ont frappé deux fois. De plus, elle dit que parmi les sommets restants (ceux qui ont frappé une fois), vous devez en reprendre au moins la moitié.

Nous venons d'apprendre à ne pas laisser plus de 2k sommets dans un graphique. En effet, si le reste de la réponse est au moins la moitié de tous les sommets, alors le nombre total de sommets ne dépasse pas 2k .

Ici, j'ai réussi à faire un petit pas en avant. Il est clair que le noyau construit de cette manière dépend du type de couverture minimale des sommets dans le graphe bipartite que nous avons pris. Je voudrais prendre tel que le nombre de sommets restants soit minime. Auparavant, ils ne savaient que le faire à temps. $$$mn ^ {3/2}$. Je suis venu avec l'implémentation de cet algorithme dans le temps $$$mn ^ {1/2}$Ainsi, ce noyau peut être recherché sur des graphiques de centaines de milliers de sommets à chaque étape de la ramification.

Résultat

La pratique montre que ma solution fonctionne bien sur des tests de plusieurs centaines de sommets et plusieurs milliers d'arêtes. Sur ces tests, on peut s'attendre à ce qu'une solution soit trouvée en une demi-heure. La probabilité de trouver une réponse dans une période de temps acceptable augmente en principe si le graphique a beaucoup de sommets de grand degré, par exemple de 10 degrés et plus.

Pour participer au concours, les décisions devaient être envoyées à optil.io . A en juger par la plaque qui y est présentée, ma décision sur les tests ouverts se classe troisième sur vingt avec une large marge par rapport au second. Pour être tout à fait honnête, la façon dont les décisions seront évaluées lors de la compétition n'est pas tout à fait claire: par exemple, ma décision passe moins de tests que la décision en quatrième place, mais elle fonctionne plus rapidement pour ceux qui réussissent.

Les résultats des tests fermés seront annoncés le 1er juillet.