Bienvenue à l'une des conférences de CS231n: Réseaux de neurones convolutifs pour la reconnaissance visuelle .

Table des matières

• Présentation de l'architecture
• Couches dans un réseau neuronal convolutif
  - couche convolutionnelle
  - Sous-échantillonnage de couche
  - Couche de normalisation
  - couche entièrement connectée
  - Convertissez des couches entièrement connectées en couches convolutives
• Architecture de réseau neuronal convolutif
  - Modèles de calque
  - Modèles de taille de couche
  - Étude de cas (LeNet, AlexNet, ZFNet, GoogLeNet, VGGNet)
  - Aspects informatiques
• Lectures complémentaires

Réseaux de neurones convolutifs (CNN / ConvNets)

Les réseaux de neurones convolutifs sont très similaires aux réseaux de neurones habituels que nous avons étudiés dans le dernier chapitre (se référant au dernier chapitre du cours CS231n): ils sont constitués de neurones, qui, à leur tour, contiennent des poids et des déplacements variables. Chaque neurone reçoit des données d'entrée, calcule le produit scalaire et, éventuellement, utilise une fonction d'activation non linéaire. Le réseau entier, comme précédemment, est la seule fonction d'évaluation différenciable: de l'ensemble initial de pixels (image) à une extrémité à la distribution de probabilité d'appartenir à une classe particulière à l'autre extrémité. Ces réseaux ont toujours une fonction de perte (par exemple, SVM / Softmax) sur la dernière couche (entièrement connectée), et tous les conseils et recommandations qui ont été donnés dans le chapitre précédent concernant les réseaux de neurones ordinaires sont également pertinents pour les réseaux de neurones convolutifs.

Alors qu'est-ce qui a changé? L'architecture des réseaux de neurones convolutifs implique explicitement l'obtention d'images en entrée, ce qui nous permet de prendre en compte certaines propriétés des données d'entrée dans l'architecture de réseau elle-même. Ces propriétés vous permettent de mettre en œuvre la fonction de distribution directe plus efficacement et de réduire considérablement le nombre total de paramètres dans le réseau.

Présentation de l'architecture

Nous rappelons les réseaux neuronaux ordinaires. Comme nous l'avons vu dans le chapitre précédent, les réseaux de neurones reçoivent des données d'entrée (un seul vecteur) et les transforment en «poussant» à travers une série de couches cachées . Chaque couche cachée est constituée d'un certain nombre de neurones, chacun étant connecté à tous les neurones de la couche précédente et où les neurones de chaque couche sont complètement indépendants des autres neurones au même niveau. La dernière couche entièrement connectée est appelée la «couche de sortie» et dans les problèmes de classification est la distribution des notes par classe.

Les réseaux de neurones conventionnels ne s'adaptent pas bien aux images plus grandes . Dans l'ensemble de données CIFAR-10, les images sont de taille 32x32x3 (32 pixels de haut, 32 pixels de large, 3 canaux de couleur). Pour traiter une telle image, un neurone entièrement connecté dans la première couche cachée d'un réseau neuronal normal aura 32x32x3 = 3072 poids. Cette quantité est toujours acceptable, mais il devient évident qu'une telle structure ne fonctionnera pas avec des images plus grandes. Par exemple, une image plus grande - 200x200x3, fera que le nombre de poids deviendra 200x200x3 = 120 000. De plus, nous aurons besoin de plus d'un tel neurone, donc le nombre total de poids commencera rapidement à augmenter. Il devient évident que la connectivité est excessive et qu'un grand nombre de paramètres conduira rapidement le réseau à une reconversion.

Représentations 3D des neurones . Les réseaux de neurones convolutifs utilisent le fait que les données d'entrée sont des images, ils forment donc une architecture plus sensible pour ce type de données. En particulier, contrairement aux réseaux de neurones conventionnels, les couches du réseau de neurones convolutifs organisent les neurones en 3 dimensions - largeur, hauteur, profondeur ( Remarque : le mot «profondeur» fait référence à la 3e dimension des neurones d'activation, et non la profondeur du réseau de neurones lui-même mesurée nombre de couches). Par exemple, les images d'entrée du jeu de données CIFAR-10 sont des données d'entrée dans une représentation 3D, dont la dimension est 32x32x3 (largeur, hauteur, profondeur). Comme nous le verrons plus loin, les neurones d'une couche seront associés à un petit nombre de neurones de la couche précédente, au lieu d'être connectés à tous les neurones précédents de la couche. De plus, la couche de sortie de l'image de l'ensemble de données CIFAR-10 aura une dimension de 1 × 1 × 10, car à l'approche de la fin du réseau neuronal, nous réduirons la taille de l'image à un vecteur d'estimations de classe situé le long de la profondeur (3e dimension).

Visualisation:

Réseau de neurones standard	Réseau de neurones convolutifs

Côté gauche: réseau neuronal standard à 3 couches.
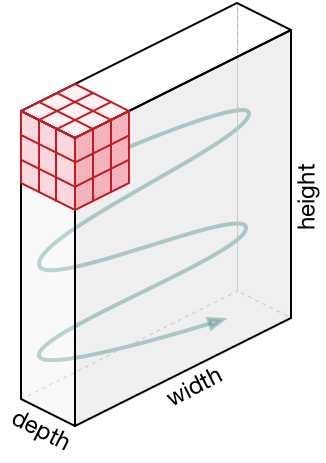
A droite: le réseau neuronal convolutionnel a ses neurones en 3 dimensions (largeur, hauteur, profondeur), comme indiqué sur l'une des couches. Chaque couche de réseau neuronal convolutif convertit une représentation 3D de l'entrée en une représentation 3D de la sortie sous forme de neurones d'activation. Dans cet exemple, le calque d'entrée rouge contient l'image, donc sa taille sera égale à la taille de l'image, et la profondeur sera de 3 (trois canaux - rouge, vert, bleu).

Le réseau neuronal convolutionnel est constitué de couches. Chaque couche est une API simple: convertit la représentation 3D d'entrée en représentation 3D de sortie d'une fonction différenciable, qui peut ou non contenir des paramètres.

Couches utilisées pour construire des réseaux de neurones convolutifs

Comme nous l'avons déjà décrit ci-dessus, un simple réseau neuronal convolutionnel est un ensemble de couches, où chaque couche convertit une représentation en une autre en utilisant une certaine fonction différenciable. Nous utilisons trois types principaux de couches pour construire des réseaux de neurones convolutionnels: une couche convolutionnelle , une couche de sous-échantillonnage et une couche entièrement connectée (la même que celle que nous utilisons dans un réseau neuronal normal). Nous organisons ces couches séquentiellement pour obtenir l'architecture SNA.

Exemple d'architecture: vue d'ensemble. Ci-dessous, nous allons plonger dans les détails, mais pour l'instant, pour l'ensemble de données CIFAR-10, l'architecture de notre réseau neuronal convolutionnel peut être [INPUT -> CONV -> RELU -> POOL -> FC] . Maintenant plus en détail:

• INPUT [32x32x3] contiendra les valeurs originales des pixels de l'image, dans notre cas, l'image est large de 32 pixels, haute de 32 pixels et 3 canaux de couleur R, G, B.
• CONV couche CONV produira un ensemble de neurones de sortie qui seront associés à la zone locale de l'image source d'entrée; chacun de ces neurones calculera le produit scalaire entre ses poids et la petite partie de l'image originale à laquelle il est associé. La valeur de sortie peut être une représentation 3D de 323212 , si, par exemple, nous décidons d'utiliser 12 filtres.
• RELU couche RELU appliquera la fonction d'activation d'élément max(0, x) . Cette conversion ne changera pas la dimension des données - [32x32x12] .
• POOL couche POOL effectuera l'opération d'échantillonnage de l'image en deux dimensions - hauteur et largeur, ce qui nous donnera par conséquent une nouvelle représentation 3D [161612] .
• FC couche FC (couche entièrement connectée) calculera les notes par classes, la dimension résultante sera [1x1x10] , où chacune des 10 valeurs correspondra aux notes d'une classe particulière parmi 10 catégories d'images de CIFAR-10. Comme dans les réseaux de neurones conventionnels, chaque neurone de cette couche sera associé à tous les neurones de la couche précédente (représentation 3D).

C'est ainsi que le réseau de neurones convolutionnels transforme l'image originale, couche par couche, de la valeur de pixel initiale à l'estimation de classe finale. Notez que certains calques contiennent des options et d'autres non. En particulier, les couches CONV/FC effectuent une transformation, qui est non seulement une fonction qui dépend des données d'entrée, mais dépend également des valeurs internes des poids et des déplacements dans les neurones eux-mêmes. RELU/POOL couches RELU/POOL , RELU/POOL revanche, utilisent des fonctions non paramétrées. Les paramètres des couches CONV/FC seront entraînés par descente de gradient afin que l'entrée reçoive les étiquettes de sortie correctes correspondantes.

Pour résumer:

• L'architecture du réseau neuronal convolutionnel, dans sa représentation la plus simple, est un ensemble ordonné de couches qui transforme la représentation d'une image en une autre représentation, par exemple, des estimations d'appartenance à une classe.
• Il existe plusieurs types de couches (CONV - couche convolutionnelle, FC - entièrement connecté, RELU - fonction d'activation, POOL - couche de sous-échantillon - la plus populaire).
• Chaque couche d'entrée reçoit une représentation 3D, la convertit en une représentation 3D de sortie à l'aide d'une fonction différenciable.
• Chaque couche peut et peut ne pas avoir de paramètres (CONV / FC - avoir des paramètres, RELU / POOL - non).
• Chaque couche peut et peut ne pas avoir d'hyper paramètres (CONV / FC / POOL - avoir, RELU - non)

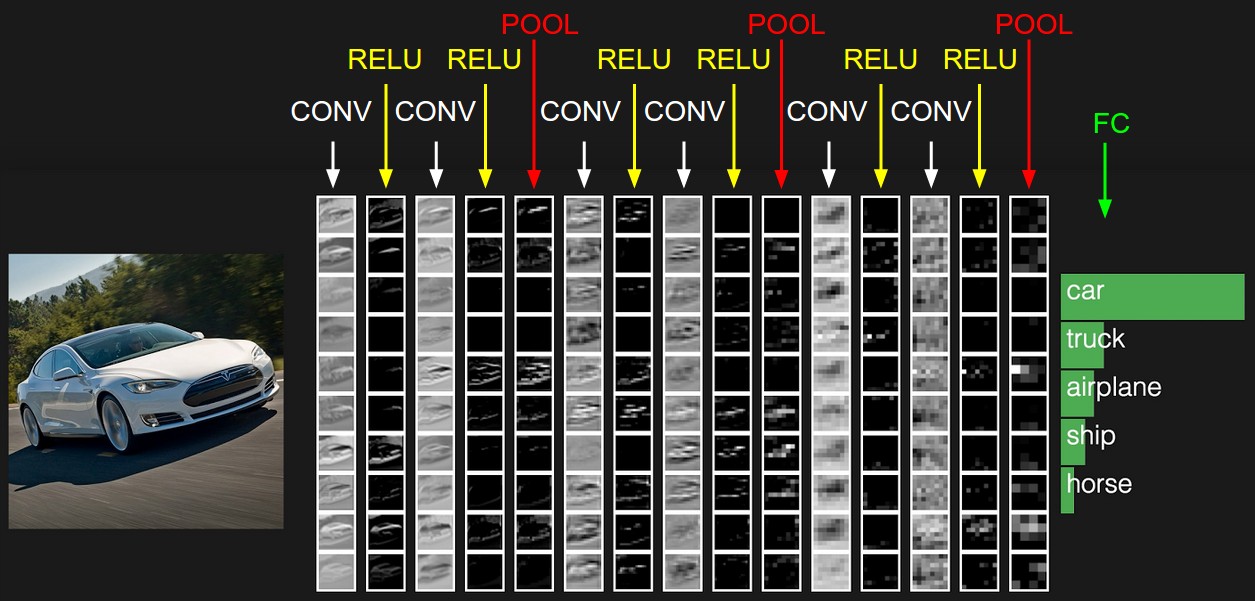
La représentation initiale contient les valeurs en pixels de l'image (à gauche) et les estimations pour les classes auxquelles appartient l'objet dans l'image (à droite). Chaque transformation de vue est marquée comme une colonne.

Couche convolutionnelle

La couche convolutionnelle est la couche principale de la construction de réseaux de neurones convolutionnels.

Aperçu sans plonger dans les caractéristiques du cerveau. Essayons d'abord de comprendre ce que la couche CONV calcule toujours sans immerger et toucher le sujet du cerveau et des neurones. Les paramètres de la couche convolutionnelle consistent en un ensemble de filtres formés. Chaque filtre est une petite grille sur la largeur et la hauteur, mais s'étendant sur toute la profondeur de la représentation d'entrée.

Par exemple, un filtre standard sur la première couche d'un réseau neuronal convolutionnel peut avoir des dimensions 5x5x3 (5px - largeur et hauteur, 3 - le nombre de canaux de couleur). Lors d'un passage direct, nous déplaçons (pour être exact - nous réduisons) le filtre le long de la largeur et de la hauteur de la représentation d'entrée et calculons le produit scalaire entre les valeurs du filtre et les valeurs correspondantes de la représentation d'entrée en tout point. Dans le processus de déplacement du filtre le long de la largeur et de la hauteur de la représentation d'entrée, nous formons une carte d'activation bidimensionnelle qui contient les valeurs d'application de ce filtre à chacune des zones de la représentation d'entrée. Intuitivement, il devient clair que le réseau apprendra aux filtres à s'activer lorsqu'ils voient un certain signe visuel, par exemple, une ligne droite à un certain angle ou des représentations en forme de roue à des niveaux supérieurs. Maintenant que nous avons appliqué tous nos filtres à l'image d'origine, par exemple, il y en avait 12. À la suite de l'application de 12 filtres, nous avons reçu 12 cartes d'activation de dimension 2. Pour produire une représentation de sortie, nous combinons ces cartes (séquentiellement dans la 3ème dimension) et obtenons une représentation dimension [LxHx12].

Un aperçu auquel nous connectons le cerveau et les neurones. Si vous êtes un fan du cerveau et des neurones, vous pouvez imaginer que chaque neurone "regarde" une grande partie de la représentation d'entrée et transfère des informations sur cette section aux neurones voisins. Ci-dessous, nous discuterons des détails de la connectivité des neurones, de leur emplacement dans l'espace et du mécanisme de partage des paramètres.

Connectivité locale. Lorsque nous traitons des données d'entrée avec un grand nombre de dimensions, par exemple, comme dans le cas des images, alors, comme nous l'avons déjà vu, il n'est absolument pas nécessaire de connecter les neurones avec tous les neurones de la couche précédente. Au lieu de cela, nous ne connecterons les neurones qu'aux zones locales de la représentation d'entrée. Le degré de connectivité spatiale est l'un des hyper-paramètres et est appelé le champ récepteur (le champ récepteur d'un neurone est la taille du même noyau de filtre / convolution). Le degré de connectivité le long de la 3ème dimension (profondeur) est toujours égal à la profondeur de la représentation originale. Il est très important de se concentrer à nouveau sur ce point, attention à la façon dont nous définissons les dimensions spatiales (largeur et hauteur) et la profondeur: les connexions neuronales sont locales en largeur et en hauteur, mais s'étendent toujours sur toute la profondeur de la représentation d'entrée.

Exemple 1. Imaginez que la représentation d'entrée ait une taille de 32x32x3 (RGB, CIFAR-10). Si la taille du filtre (champ récepteur du neurone) est de 5 × 5, alors chaque neurone de la couche convolutionnelle aura des poids dans la région 5 × 5 × 3 de la représentation originale, ce qui conduira finalement à l'établissement de 5 × 5 × 3 = 75 liaisons (poids) + 1 paramètre de décalage. Veuillez noter que le degré de connectivité en profondeur doit être égal à 3, car il s'agit de la dimension de la représentation d'origine.

Exemple 2. Imaginez que la représentation d'entrée ait une taille de 16x16x20. En utilisant comme exemple le champ récepteur d'un neurone de taille 3x3, chaque neurone de couche convolutionnelle aura 3x3x320 = 180 connexions (poids) + 1 paramètre de déplacement. Notez que la connectivité est locale en largeur et en hauteur, mais complète en profondeur (20).

# 1	# 2

Du côté gauche: la représentation d'entrée est affichée en rouge (par exemple, une image de taille 32x332 CIFAR-10) et un exemple de la représentation des neurones dans la première couche convolutionnelle. Chaque neurone de la couche convolutionnelle n'est associé qu'à la zone locale de la représentation d'entrée, mais complètement en profondeur (dans l'exemple, le long de tous les canaux de couleur). Veuillez noter qu'il y a beaucoup de neurones dans l'image (dans l'exemple - 5) et qu'ils sont situés le long de la 3ème dimension (profondeur) - des explications concernant cet arrangement seront données ci-dessous.
Du côté droit: les neurones du réseau neuronal restent inchangés: ils calculent toujours le produit scalaire entre leurs poids et les données d'entrée, appliquent la fonction d'activation, mais leur connectivité est maintenant limitée par la zone locale spatiale.

L'emplacement spatial. Nous avons déjà compris la connectivité de chaque neurone dans la couche convolutionnelle avec la représentation d'entrée, mais nous n'avons pas encore discuté du nombre de ces neurones ni de leur localisation. Trois hyper paramètres affectent la taille de la vue de sortie: la profondeur , le pas et l' alignement .

1. La profondeur de la représentation de sortie est un hyper paramètre: elle correspond au nombre de filtres que nous voulons appliquer, chacun apprenant autre chose dans la représentation originale. Par exemple, si la première couche convolutionnelle reçoit une image en entrée, différents neurones le long de la 3ème dimension (profondeur) peuvent être activés en présence de différentes orientations de lignes dans une certaine zone ou de grappes d'une certaine couleur. L'ensemble des neurones qui "regardent" la même zone de la représentation d'entrée, nous l'appellerons la colonne profonde (ou "fibre" - fibre).
2. Nous devons déterminer le pas (taille de décalage en pixels) avec lequel le filtre se déplacera. Si le pas est 1, alors nous décalons le filtre de 1 pixel en une seule itération. Si l'étape est 2 (ou, ce qui est encore moins utilisé, 3 ou plus), le décalage se produit pour tous les deux pixels en une seule itération. Une étape plus grande se traduit par une représentation de sortie plus petite.
3. Comme nous le verrons bientôt, il sera parfois nécessaire de compléter la représentation d'entrée le long des bords par des zéros. La taille d'alignement (le nombre de colonnes / lignes remplies par zéro) est également un hyper paramètre. Une caractéristique intéressante de l'utilisation de l'alignement est le fait que l'alignement nous permettra de contrôler la dimension de la représentation de sortie (le plus souvent, nous conserverons les dimensions d'origine de la vue - en préservant la largeur et la hauteur de la représentation d'entrée avec la largeur et la hauteur de la représentation de sortie).

Nous pouvons calculer la dimension finale de la représentation de sortie en la présentant en fonction de la taille de la représentation d'entrée ( W ), de la taille du champ récepteur des neurones de la couche convolutionnelle ( F ), du pas ( S ) et de la taille de l'alignement ( P ) aux frontières. Vous pouvez constater par vous-même que la formule correcte pour calculer le nombre de neurones dans la représentation de sortie est la suivante (W - F + 2P) / S + 1 . Par exemple, pour une représentation d'entrée de taille 7x7 et une taille de filtre de 3x3, étape 1 et alignement 0, nous obtenons une représentation de sortie de taille 5x5. À l'étape 2, nous obtiendrions une représentation de sortie de 3x3. Regardons un autre exemple, illustré cette fois graphiquement:

Illustration d'une disposition spatiale. Dans cet exemple, une seule dimension spatiale (axe x), un neurone avec un champ récepteur F = 3 , une taille de représentation d'entrée W = 5 et un alignement P = 1 . A gauche : le champ récepteur du neurone se déplace d'un pas S = 1 , ce qui donne en conséquence la taille de la représentation de sortie (5 - 3 + 2) / 1 + 1 = 5. A droite : le neurone utilise le champ récepteur de taille S = 2 , qui en le résultat est la taille de la représentation de sortie (5 - 3 + 2) / 2 + 1 = 3. Notez que la taille de pas S = 3 ne peut pas être utilisée, car avec cette taille de pas, le champ récepteur ne capturera pas une partie de l'image. Si nous utilisons notre formule, alors (5 - 3 + 2) = 4 n'est pas un multiple de 3. Les poids des neurones dans cet exemple sont [1, 0, -1] (comme indiqué dans l'image la plus à droite), et le décalage est nul. Ces poids sont partagés par tous les neurones jaunes.

Utilisation de l'alignement . Faites attention à l'exemple sur le côté gauche, qui contient 5 éléments à la sortie et 5 éléments à la sortie. Cela a fonctionné car la taille du champ récepteur (filtre) était de 3 et nous avons utilisé l'alignement P = 1 . S'il n'y avait pas d'alignement, la taille de la représentation de sortie serait égale à 3, car il y avait précisément autant de neurones qui pouvaient s'y adapter. En général, le réglage de la taille d'alignement P = (F - 1) / 2 avec un pas égal à S = 1 vous permet d'obtenir la taille de la représentation de sortie similaire à la représentation d'entrée. Une approche similaire utilisant l'alignement est souvent appliquée dans la pratique, et nous discuterons des raisons ci-dessous lorsque nous parlerons de l'architecture des réseaux de neurones convolutifs.

Limites de taille de pas . Veuillez noter que les hyper-paramètres responsables de l'agencement spatial sont également liés par des limitations. Par exemple, si la représentation d'entrée a une taille de W = 10 , P = 0 et la taille du champ récepteur F = 3 , alors il devient impossible d'utiliser une taille de pas égale à S = 2 , car (W - F + 2P) / S + 1 = (10 - 3 + 0) / 2 + 1 = 4,5 , ce qui donne une valeur entière du nombre de neurones. Ainsi, une telle configuration d'hyper paramètres est considérée comme invalide et les bibliothèques pour travailler avec des réseaux de neurones convolutifs lèveront une exception, forceront l'alignement ou même couperont la représentation d'entrée. Comme nous le verrons dans les sections suivantes de ce chapitre, la définition des hyper-paramètres de la couche convolutionnelle est toujours un casse-tête qui peut être réduit en utilisant certaines recommandations et «bonnes règles de tonalité» lors de la conception de l'architecture des réseaux de neurones convolutionnels.

Exemple concret . Architecture de réseau de neurones convolutifs Krizhevsky et al. , qui a remporté le concours ImageNet en 2012, a reçu 227x227x3 images. Sur la première couche convolutive, elle a utilisé un champ récepteur de taille F = 11 , étape S = 4 et d'alignement de taille P = 0 . Puisque (227 - 11) / 4 + 1 = 55, et que la couche convolutionnelle avait une profondeur de K = 96 , la dimension de sortie de la présentation était de 55x55x96. Chacun des neurones 55x55x96 dans cette représentation était associé à une région de taille 11x11x3 dans la représentation d'entrée. De plus, les 96 neurones de la colonne profonde sont associés à la même région 11x11x3, mais avec des poids différents. Et maintenant, un peu d'humour - si vous décidez de vous familiariser avec le document d'origine (étude), notez que le document prétend que l'entrée reçoit des images 224x224, ce qui ne peut pas être vrai, car (224-11) / 4 + 1 ne donne en aucun cas une valeur entière. Ce genre de situation est souvent confondu pour les personnes dans des histoires avec des réseaux de neurones convolutionnels. Je suppose qu'Alex a utilisé la taille d'alignement P = 3 , mais a oublié de le mentionner dans le document.

Options de partage. Le mécanisme de partage des paramètres dans les couches convolutives est utilisé pour contrôler le nombre de paramètres. Faites attention à l'exemple ci-dessus, car vous pouvez voir qu'il y a 55x55x96 = 290,400 neurones sur la première couche convolutionnelle et chacun des neurones a 11x11x3 = 363 poids + 1 valeur de décalage. Au total, si l'on multiplie ces deux valeurs, on obtient 290400x364 = 105 705 600 paramètres uniquement sur la première couche du réseau neuronal convolutif. De toute évidence, cela est d'une grande importance!

Il s'avère qu'il est possible de réduire considérablement le nombre de paramètres en faisant une hypothèse: si une propriété calculée en position (x, y) nous importe, alors cette propriété calculée en position (x2, y2) nous importera également. En d'autres termes, désignant une «couche» bidimensionnelle en profondeur comme une «couche profonde» (par exemple, la vue [55x55x96] contient 96 couches profondes, chacune de 55x55), nous construirons des neurones en profondeur avec les mêmes poids et déplacements. Avec ce schéma de partage des paramètres, la première couche convolutionnelle dans notre exemple contiendra désormais 96 ensembles de poids uniques (chaque ensemble pour chaque couche de profondeur), au total, il y aura 96x11x11x3 = 34848 poids uniques ou 34944 paramètres (+96 décalages). De plus, tous les neurones 55x55 de chaque couche profonde utiliseront désormais les mêmes paramètres. En pratique, pendant la rétropropagation, chaque neurone dans cette représentation calculera le gradient pour ses propres poids, mais ces gradients seront additionnés sur chaque couche de profondeur et ne mettront à jour qu'un seul ensemble de poids à chaque niveau.

Notez que si tous les neurones de la même couche profonde utilisaient les mêmes poids, alors pour une propagation directe à travers la couche convolutionnelle, la convolution entre les valeurs des poids des neurones et les données d'entrée serait calculée. C'est pourquoi il est habituel d'appeler un seul ensemble de poids - un filtre (noyau) .

Des exemples de filtres obtenus en entraînant le modèle Krizhevsky et al. Chacun des 96 filtres montrés ici est de taille 11x11x3 et chacun d'eux est partagé par tous les neurones 55x55 d'une couche profonde. Veuillez noter que l'hypothèse de partager les mêmes poids est logique: si la détection d'une ligne horizontale est importante dans une partie de l'image, il est intuitivement clair qu'une telle détection est importante dans une autre partie de cette image. Par conséquent, cela n'a aucun sens de se recycler à chaque fois pour trouver des lignes horizontales dans chacun des 55x55 endroits différents de l'image dans la couche convolutionnelle.

Il ne faut pas oublier que l'hypothèse d'un partage des paramètres n'est pas toujours logique. Par exemple, si une image avec une structure centrée est alimentée à l'entrée d'un réseau neuronal convolutif, où nous aimerions pouvoir apprendre une propriété dans une partie de l'image et une autre propriété dans l'autre partie de l'image. Un exemple pratique est les images à face centrée. On peut supposer que différents signes oculaires ou capillaires peuvent être identifiés dans différentes zones de l'image.Par conséquent, dans ce cas, la relaxation des poids est utilisée et la couche est appelée connectée localement .

Quelques exemples . Les discussions précédentes devraient être transférées au plan des spécificités et sur des exemples avec du code. Imaginez que la représentation d'entrée est un tableau numpy de X Ensuite:

• La colonne profonde ( thread ) à la position (x,y) sera représentée comme suit X[x,y,:] .
• La couche profonde , ou comme nous l'appelions précédemment une telle couche - la carte d'activation à la profondeur d sera représentée comme suit X[:,:,d] .

Un exemple de couche convolutionnelle . , X X.shape: (11,11,4) . , P=1 , () F=5 S=1 . 44, — (11-5)/2+1=4. ( V ), ( ):

• V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
• V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
• V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
• V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0

, numpy , * . , W0 b0 . W0 W0.shape: (5,5,4) , 5, 4. . , , 2 ( ). :

• V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1
• V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1
• V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1
• V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1
• V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1 (, y )
• V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1 (, )

— W1 b1 . , V . , , , ReLU , . .

. :

• W1 x H1 x D1
• 4 -:
  
  • K ,
  • F ,
  • S ,
  • P .
• W2 x H2 x D2 ,
  
  • W2 = (W1 — F + 2P)/S + 1
  • H2 = (H1 — F + 2P)/S + 1
  • D2 = K
• F x F x D1 , (F x F x D1) x K K .
• , d - ( W2 x H2 ) d - S d -.

- F = 3, S = 1, P = 1 . . " ".

. . 3D- ( — , — , — ), — . W1 = 5, H1 = 5, D1 = 3 , K = 2, F = 3, S = 2, P = 1 . , 33, 2. (5 — 3 + 2)/2 + 1 = 3. , , P = 1 . , () , .

( , html+css , )

. (). :

1. im2col . , 227x227x3 11113 4, 11113 = 363 . , 4 , (227 — 11) / 4 + 1 = 55 , X_col 3633025, 3025. , , , (), .
2. . , 96 11113, W_row 96363.
3. — np.dot(W_row, X_col) , . 963025.
4. 555596.

, , — , . , , — (, BLAS API). , im2col , .

. ( ) ( , ) ( - ). , .

11 . 11, Network in Network . , 11, , . , 2- , 11 ( ). , , 3- , . , 32323, 11, , , 3 (R, G, B — , ).

. - . . , . w 3 x : w[0] x[0] + w[1] x[1] + w[2] x[2] . 0. 1 : w[0] x[0] + w[1] x[2] + w[2] x[4] . "" 1 . , . , 2 33, , 55 ( 55 ). .

— . , , . , MAX. 22 2, 2 , 75% . MAX 22. . , :

• W1 x H1 x D1
• 2 -:
  
  • F ,
  • S ,
• W2 x H2 x D2 , :
  
  • W2 = (W1 — F)/S + 1
  • H2 = (H1 — F)/S + 1
  • D2 = D1
• ,
• (zero-padding ).

, : F=3, S=2 ( ), — F=2, S=2 . - .

. , , , L2-. , , .

#1	#2

. : 22422464 22 2, 11211264. , . : — (max-pooling), 2. 4 ( 22)

. , max(a,b) — . , ( ), .

. , . , : , . . , (VAEs) (GANs). , - , .

, , . , , . .

, . .

, , ( ). - , . , :

• , . , , , , , .
• , . , K=4096 ( ), 7712 - F=7, P=0, S=1, K=4096 . , 114096, .

. , . , 2242243 77512 ( AlexNet, , 5 , 7 — 224/2/2/2/2/2 = 7). AlexNet 4096 , , 1000 , . :

• , "" 77512, F=7 , 114096.
• F=1 , 114096.
• F=1 , 111000.

, , ( ) W . , "" () .

, 224224 , 77512 — 32 , 384384 1212512, 384/32 = 12. , , , 661000, (12 — 7)/1 + 1 = 6. , 111000 66 384384 .

( ) 384384, 224244 32 , , .

, , 36 , 36 . , , . .

, , 32 ? ( ). , 16 , 2 : 16 .

, , 3 : , ( , ) . ReLU , - . .

CONV-RELU-, POOL- , . - . , , . , :

 INPUT -> [[CONV -> RELU]*N -> POOL?] * M -> [FC -> RELU]*K -> FC 

* , POOL? . , N >= 0 ( N <= 3 ), M >= 0 , K >= 0 ( K < 3 ). , , :

• INPUT -> FC , . N = M = K = 0 .
• INPUT -> CONV -> RELU -> FC
• INPUT -> [CONV -> RELU -> POOL] * 2 -> FC -> RELU -> FC , .
• INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL] * 3 -> [FC -> RELU] * 2 -> FC . 2 . , , .

. 3 33 ( RELU , ). "" 33 . "" 33 , — 55. "" 33 , — 77. , 33 77. "" 77 ( ) , . -, , 3 , . -, C , , 77 (C(77)) = 49xxC , 33 3((33)) = 27 . , , . — , .

. , , Google, Microsoft. .

: , ImageNet. , , 90% . — " ": , , , ImageNet — , . .

-, . , :

( ) 2 . 32 (, CIFAR-10), 64, 96 (, STL-10), 224 (, ImageNet), 384 512.

(, 33 , 55), S=1 , , , . , F=3 P=1 . F=5, P=2 . F , P=(F-1)/2 . - ( 77), .

. 22 ( F=2 ) 2 ( S=2 ). , 75% (- , ). , , 33 ( ) 2 ( ). 33 , . .

. , , . , 1 , , .

1 ? . , 1 ( ), .

? , . , , , .

. ( ), , . , 64 33 1 2242243, 22422464. , , 10 , 72 ( , ). GPU, . , 77 2. , AlexNet, 1111 4.

. :

• LeNet . Yann LeCun 1990. LeNet , ZIP-, .
• AlexNet . , , Alex Krizhevsky, Ilya Sutskever Geoff Hinton. AlexNet ImageNet ILSVRC 2012 ( : 16% 26%). LeNet, , ( ).
• ZFNet . ILSVRC 2013 Matthew Zeiler Rob Fergus. ZFNet. AlexNet, -, .
• GoogLeNet . ILSVRC 2014 Szegedy et al. Google. Inception-, (4 60 AlexNet). , , . , — Inveption-v4.
• VGGNet . 2014 ILSVRC Karen Simonyan Andrew Zisserman, VGGNet. , . 16 + (33 22 ). . VGGNet — (140). , , , .
• ResNet . Residual- Kaiming He et al. ILSVRC 2015. . . ( 2016).

VGGNet . VGGNet . VGGNet , 33, 1 1, 22 2. ( ) :

 INPUT: [224x224x3] memory: 224*224*3=150K weights: 0 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*3)*64 = 1,728 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*64)*64 = 36,864 POOL2: [112x112x64] memory: 112*112*64=800K weights: 0 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*64)*128 = 73,728 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*128)*128 = 147,456 POOL2: [56x56x128] memory: 56*56*128=400K weights: 0 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*128)*256 = 294,912 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 POOL2: [28x28x256] memory: 28*28*256=200K weights: 0 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*256)*512 = 1,179,648 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 POOL2: [14x14x512] memory: 14*14*512=100K weights: 0 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 POOL2: [7x7x512] memory: 7*7*512=25K weights: 0 FC: [1x1x4096] memory: 4096 weights: 7*7*512*4096 = 102,760,448 FC: [1x1x4096] memory: 4096 weights: 4096*4096 = 16,777,216 FC: [1x1x1000] memory: 1000 weights: 4096*1000 = 4,096,000 TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd) TOTAL params: 138M parameters 

, , ( ) , . 100 140 .

. GPU 3/4/6 , GPU — 12 . , :

• : , ( ). , . , .
• : , , . , , 3 .
• , , ..

(, ), . , 4 ( 4 , — 8), 1024 , , . " ", , .

… call-to-action — , share :)
YouTube
Télégramme
VKontakte