👷 🐜 📤 Le monde de l'hypersphère tridimensionnelle. Traçage de rayons géodésiques dans un univers fermé à géométrie sphérique 🎉 😅 🖕🏽

Aimeriez-vous voir le monde à travers les yeux d'une créature vivant dans un univers fermé compact avec une géométrie sphérique? Voir le monde sans nuit? Un monde où l'autre pôle de la planète est visible dans le ciel? Un monde où il n'y a pas de différence entre une éclipse solaire et lunaire? Bienvenue au chat!

Présentation Monde fermé à deux dimensions

Afin de mieux comprendre ce qui va se passer ensuite, imaginez que vous êtes un être à deux dimensions et vivez dans un monde à deux dimensions représentant une sphère. Comment allez-vous percevoir votre monde? Commençons par déterminer la position des corps. Vous pouvez déclarer le point où vous êtes le «centre de l'univers», sélectionner deux vecteurs unitaires mutuellement perpendiculaires et utiliser le système de coordonnées cartésiennes résultant au voisinage du «centre de l'univers».

Cependant, lorsque vous vous éloignez du "centre de l'univers", des choses étranges vont commencer à se produire. Ce que vous avez perçu comme des lignes perpendiculaires, à une certaine distance du "centre de l'univers" se transforme en ce que vous percevez comme des lignes parallèles ...

... Et les lignes parallèles se croisent.

La raison est simple - ce que vous percevez comme une ligne droite est en fait un grand cercle - la ligne géodésique de la sphère. Par conséquent, le système de coordonnées cartésiennes n'est pas approprié pour déterminer la position des corps dans votre monde - lorsque vous vous éloignez du "centre de l'univers", il perd son sens.

Vous devrez en choisir un autre, plus adapté à une utilisation dans votre monde, le système de coordonnées - polaire . Ce système de coordonnées est naturel et cohérent. En effet - l'angle entre l'axe polaire et la direction du corps reste constant quelle que soit la distance au corps.

Étant en mesure de déterminer la position des corps, nous pouvons explorer mentalement votre monde et décrire certains effets qui apparaissent lorsque vous vous éloignez du "centre de l'univers" et du fait que votre monde est une sphère.

La perspective inverse . Habituellement, lorsqu'un corps s'éloigne du "centre de l'univers", sa taille angulaire diminue. Cependant, à une distance de plus d'un quart de la longueur de la ligne géodésique du "centre de l'univers" avec la suppression du corps, sa taille angulaire augmentera. Cet effet est dû au fait que la distance entre les lignes géodésiques de la sphère à l'équateur augmente, et après que l'équateur diminue. Un corps éloigné à la même distance de l'équateur aura la même taille angulaire, quel que soit son côté par rapport à l'équateur. Et cette taille angulaire sera plus grande que la taille angulaire du corps à l'équateur.

Étirer le corps partout dans le ciel. Ici, le terme ciel entier est utilisé dans le sens - l'ensemble du champ de vision d'un être à deux dimensions (supérieur et inférieur ou avant et arrière). Si le corps est près du point opposé au "centre de l'univers", alors où que vous regardiez, vous rencontrerez votre regard avec ce corps. Le corps n'aura pas de point qui ne pourrait pas être vu - chaque point a une place dans le ciel. C'est le cas ultime de l'effet de perspective inverse.

Transformation symétrique tél. Si le corps est à une distance de plus de la moitié de la longueur de la ligne géodésique du "centre de l'univers", alors vous verrez ce corps transformé symétriquement - les côtés gauche et droit du corps changeront de place. Habituellement, les rayons gauche et droit émis par le "centre de l'univers" tombent sur les côtés gauche et droit du corps. Cependant, à une distance de la moitié de la longueur de la ligne géodésique du "centre de l'univers", les rayons se croisent et, après avoir traversé, tombent dans les côtés opposés du corps.

Les deuxièmes perspectives avant et arrière. Cet effet est également observé si le corps est à une distance supérieure à la moitié de la longueur de la ligne géodésique du "centre de l'univers". À des distances de la moitié aux trois quarts de la longueur de la ligne géodésique du «centre de l'univers», avec la suppression du corps, sa taille angulaire diminuera à nouveau (perspective directe). À des distances de trois quarts à toute la longueur de la ligne géodésique du «centre de l'univers», à mesure que le corps s'éloigne, sa taille angulaire augmentera à nouveau (perspective inverse). Cet effet, ainsi que l'effet de perspective inverse, est associé à un changement de la distance entre les lignes géodésiques de la sphère - sur le chemin du retour au "centre de l'univers", la distance entre les lignes géodésiques de la sphère jusqu'à l'équateur augmente et diminue après l'équateur.

Doubles. Chaque corps de votre monde aura un double - si vous voyez un corps devant vous, alors en vous retournant, vous pouvez voir son côté opposé (double). Un rayon émis le long d'un long chemin fait le tour de votre monde et pénètre à l'arrière du corps. Il convient de noter que la surface du double sera la partie de la surface que vous ne voyez pas devant vous, et elle sera transformée symétriquement. Ici, le terme surface est utilisé dans le sens - la limite d'un corps bidimensionnel perçu par un être bidimensionnel - tel qu'il est appliqué à un cercle, il s'agit en fait d'un arc circulaire perçu par un être bidimensionnel comme un segment.Cependant, pour plus de clarté, nous mettrons en évidence non seulement l'arc, mais aussi la partie du cercle située derrière lui.

Le passage du corps par un point opposé au «centre de l'univers». Étant donné que l'effet d'étirement du corps vers le ciel entier est très inhabituel, nous allons l'examiner plus en détail. Sur les figures: le voisinage d'un point opposé au «centre de l'univers».

On voit que:

premièrement, la surface du corps devant vous augmente (peinte en bleu) et celle derrière vous diminue (peinte en bleu); en même temps, les deux surfaces ont les mêmes dimensions angulaires - c'est-à-dire que la surface du corps située devant vous est contractée (la plus grande partie de la surface se trouve à l'intérieur de chaque degré) et celle située derrière vous est étirée (toute la plus petite partie de la surface se trouve à l'intérieur de chaque degré)
lorsque le corps touche un point opposé au "centre de l'univers", la taille angulaire des deux surfaces est de 180 degrés - une moitié du ciel (devant vous) occupe toute la surface du corps, et la seconde moitié du ciel (derrière vous) est occupée par un point allongé à l'arrière du corps
tandis que le centre du corps est aligné avec le point opposé au "centre de l'univers", le processus de traction et d'étirement inversé
lorsque le corps est situé en un point opposé au "centre de l'univers", sa surface n'est pas déformée et s'étend sur tout le ciel
le corps glissant d'un point opposé au «centre de l'univers» ressemble

Double horizon. Imaginez que vous vivez sur une planète à deux dimensions. En regardant vers le bas, vous voyez la surface de votre côté de la planète, et en levant, vous voyez ... la surface de l'arrière de la planète. De plus, il sera très resserré - vous pouvez voir à la fois la surface de l'arrière de la planète et la partie de la surface de votre côté de la planète qui est derrière votre dos derrière l'horizon - vous pouvez voir tout cela au-dessus de votre tête. Le ciel sera présenté sous la forme d'une bande étroite comme un fil, prise en sandwich par le haut et par le bas par les horizons de votre et des côtés inversés de la planète. C'est une combinaison de l'effet d'étirement du corps sur tout le ciel et de l'effet d'un double. En général, dans votre monde, si rien ne dérange votre regard, alors juste devant vous, vous pouvez voir votre nuque ... une nuque si saine, dans tous ses détails ... étendue à tout le ciel)

Un monde sans nuit. Imaginez que la planète à deux dimensions sur laquelle vous vivez tourne autour d'une étoile à deux dimensions. La lumière émise par une étoile sur un court chemin tombe du côté diurne de la planète. Dans le même temps, la lumière émise par une étoile le long d'un long chemin fait le tour de votre monde et tombe du côté nuit de la planète. La nuit n'existe plus. Il ne reste que des couchers et levers de soleil, qui se produiront simultanément - lorsque le côté de l'étoile face à vous commence à dépasser l'horizon, le côté arrière de l'étoile commence à s'élever derrière vous par derrière l'horizon. Bien sûr, vous pouvez mettre en évidence le vrai coucher de soleil et l'aube le long du chemin que la lumière a traversé, mais il sera presque impossible de les distinguer des doubles.

Il existe également un cas extrême. Si la planète n'a pas de chance et qu'elle est au point de l'étoile opposée, alors l'étoile sera étendue à tout le ciel, mais il sera problématique de l'admirer, car toute la lumière émise par l'étoile tombera sur la planète (en l'absence d'absorption et de diffusion de lumière par le milieu interplanétaire).

Éclipses solaires et lunaires. Imaginez qu'un satellite naturel bidimensionnel tourne autour d'une planète bidimensionnelle sur laquelle vous vivez. Lorsqu'un satellite se place entre une planète et une étoile, son ombre tombe sur la planète. D'autre part, en même temps, la planète se situe entre la lumière émise par l'étoile le long d'un long chemin et le satellite, c'est-à-dire que l'ombre de la planète tombe sur le satellite. Une éclipse solaire et lunaire simultanée se produit. Bien sûr, il est possible de distinguer les vraies éclipses solaires et lunaires le long du chemin parcouru par la lumière, mais il sera pratiquement impossible de les distinguer des jumeaux. Tomber dans l'ombre tombant sur la planète et son satellite pendant les éclipses est le seul moyen d'être dans le noir dans votre monde)

Monde clos tridimensionnel

Ci-dessus, nous avons examiné le monde merveilleux d'un être à deux dimensions. Et nous, êtres tridimensionnels? Quelle est la géométrie de l'univers ? Malheureusement, la science ne peut pas encore répondre à cette question. Principalement les propriétés et la taille de l'Univers interfèrent. Essayons d'aider la science. Nous sélectionnons comme candidat l'univers fermé le plus intéressant à géométrie sphérique et l'examinons visuellement. Y aura-t-il des effets découverts par nous pour un analogue bidimensionnel? Peut-être que nous apprendrons quelque chose de nouveau? Quelque chose que vous ne vous attendiez pas à savoir? Ou même voir ce que nous voyons tous les jours, mais ne faites pas attention à cela? À quoi ressemblera un tel univers?

Modèle

Nous explorerons le monde, qui est une hypersphère tridimensionnelle (3 sphères) - c'est-à-dire une sphère située dans un espace quadridimensionnel. Nous choisissons un type d'objets pour la visualisation - une sphère (une sphère 2 appartenant à une sphère 3).

Concepts et relations de base

Coordonnées cartésiennes dans un espace à quatre dimensions - nous les désignerons comme

$(x_0, x_1, x_2, x_3)$ - c'est en fait

$(x, y, z, w)$ .

Coordonnées hypersphériques dans un espace à quatre dimensions (nous n'utilisons que des angles, car le rayon de notre monde sera une constante) - nous les désignerons comme

$(a_0, a_1, a_2)$ - c'est en fait

$(\ phi, \ theta, \ psi)$ .

3 sphères centrées à l'origine - un ensemble de points dont le vecteur de rayon a une longueur égale au rayon de la 3 sphères

$R$ Est notre monde

$\ quad \ quad x_0 ^ 2 + x_1 ^ 2 + x_2 ^ 2 + x_3 ^ 2 = R ^ 2$

2 sphères appartenant à la 3 sphères - un ensemble de points dont le vecteur de rayon a une longueur égale au rayon de la 3 sphères

$R$ et forme avec le vecteur rayon du centre de la sphère 2

$c$ angle égal au rayon angulaire de la sphère 2

$r_a$ Nos objets de visualisation sont-ils

$\ quad \ quad x_0 c_0 + x_1 c_1 + x_2 c_2 + x_3 c_3 = R ^ 2 \ cos r_a$

où

$\ quad \ quad r_a = r / R$

$\ quad \ quad r$ - rayon géodésique d'une sphère à 2

Rayon géodésique, angulaire et conditionnel - afin de mieux comprendre ce que c'est, considérons un analogue bidimensionnel d'une sphère 2 appartenant à une sphère 3 - un cercle appartenant à une sphère.

L'arc rouge sur la figure est le rayon géodésique du cercle

$r$ . Le coin rouge sur le côté droit de la figure est le rayon angulaire du cercle

$r_a = r / R$ . La hauteur du triangle sur le côté droit de la figure est le rayon conditionnel du cercle

$r_n = R \ sin r_a$ .

Transition des coordonnées hypersphériques

$(a_0, a_1, a_2)$ au cartésien

$(x_0, x_1, x_2, x_3)$

$\ quad \ quad x_0 = R \ sin a_2 \ sin a_1 \ cos a_0$

$\ quad \ quad x_1 = R \ sin a_2 \ sin a_1 \ sin a_0$

$\ quad \ quad x_2 = R \ sin a_2 \ cos a_1$

$\ quad \ quad x_3 = R \ cos a_2$

où

$\ quad \ quad a_0$ varie de

$0$ avant

$2 \ pi$

$\ quad \ quad a_1$ varie de

$0$ avant

$\ pi$

$\ quad \ quad a_2$ varie de

$0$ avant

$\ pi$

L'intersection de la ligne géodésique d'une sphère 3 avec une sphère 2 appartenant à une sphère 3.
Ce rapport sera utilisé pour le lancer de rayons. Soit une ligne géodésique partant du pôle de la 3 sphère

$(0, 0, 0, R)$ dans la direction définie par les angles

$a_0$ et

$a_1$ - ces angles coïncident avec les angles déterminant la direction dans l'espace tridimensionnel au voisinage du pôle à 3 sphères

$(0, 0, 0, R)$

$\ quad \ quad x_0 = R \ sin a_2 \ sin a_1 \ cos a_0$

$\ quad \ quad x_1 = R \ sin a_2 \ sin a_1 \ sin a_0$

$\ quad \ quad x_2 = R \ sin a_2 \ cos a_1$

$\ quad \ quad x_3 = R \ cos a_2$

simplifiant nous avons (1)

$\ quad \ quad x_0 = r_0 \ sin a_2$

$\ quad \ quad x_1 = r_1 \ sin a_2$

$\ quad \ quad x_2 = r_2 \ sin a_2$

$\ quad \ quad x_3 = r_3 \ cos a_2$

où

$\ quad \ quad r_0 = R \ sin a_1 \ cos a_0$

$\ quad \ quad r_1 = R \ sin a_1 \ sin a_0$

$\ quad \ quad r_2 = R \ cos a_1$

$\ quad \ quad r_3 = R$

en substituant (1) dans l'équation de la sphère 2 et en simplifiant nous avons (2)

$\ quad \ quad A \ sin a_2 + B \ cos a_2 = C$

où

$\ quad \ quad A = r_0 c_0 + r_1 c_1 + r_2 c_2$

$\ quad \ quad B = r_3 c_3$

$\ quad \ quad C = R ^ 2 \ cos r_a$

en substituant (1) dans l'équation de la sphère 3 et en simplifiant nous avons (3)

$\ quad \ quad D \ sin ^ 2 a_2 + E \ cos ^ 2 a_2 = F$

où

$\ quad \ quad D = r_0 ^ 2 + r_1 ^ 2 + r_2 ^ 2$

$\ quad \ quad E = r_3 ^ 2$

$\ quad \ quad F = R ^ 2$

exprimant à partir de (2)

$\ cos a_2$ nous avons

$\ quad \ quad \ cos a_2 = (C - A \ sin a_2) / B$

remplaçant dans (3)

$\ cos a_2$ nous avons

$\ quad \ quad D \ sin ^ 2 a_2 + E / B ^ 2 (C - A \ sin a_2) ^ 2 = F$

simplifiant nous avons

$\ quad \ quad a \ sin ^ 2 a_2 + b \ sin a_2 + c = 0$

où

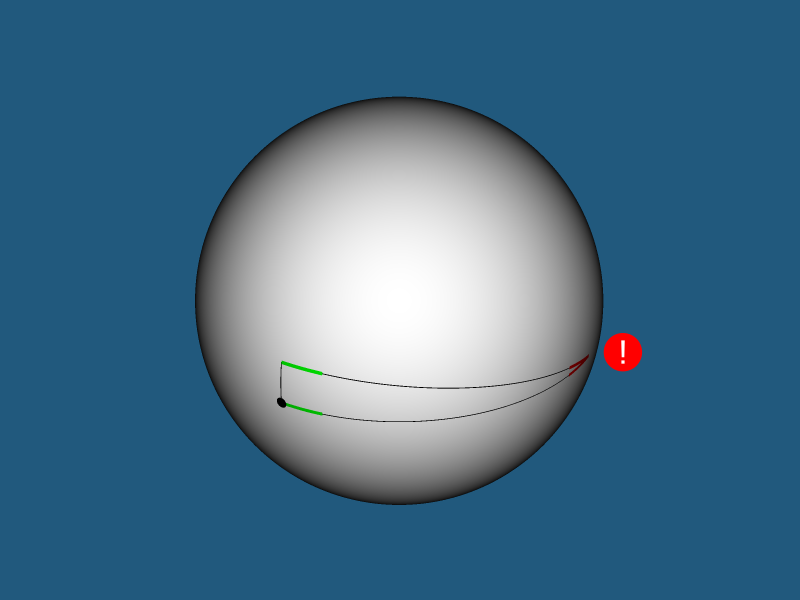
$\ quad \ quad m = E / B ^ 2$

$\ quad \ quad a = m A ^ 2 + D$

$\ quad \ quad b = -2 m A C$

$\ quad \ quad c = m C ^ 2 - F$

Un point sur la continuation de la ligne géodésique d'une sphère 3 passant par deux points.
Cette relation sera utilisée pour trouver les coordonnées de texture et la normale externe en un point arbitraire de la sphère 2 appartenant à la sphère 3. Soit

$\ quad \ quad O$ - Centre à 3 sphères

$\ quad \ quad A$ - centre de la 2 sphères

$\ quad \ quad B$ Est un point arbitraire de la sphère 2

$\ quad \ quad C$ - le point souhaité se situant sur le prolongement de la ligne géodésique

$AB$ à une petite distance angulaire

$\ delta$ du point

$B$

$\ quad \ quad D$ - point d'intersection des lignes

$AB$ et

$OC$

$\ quad \ quad E$ - le point d'intersection de la ligne passant par le point

$D$ perpendiculaire à droite

$AB$ et une ligne passant par un point

$O$ parallèle à droite

$AB$

$\ quad \ quad r_a$ - rayon angulaire d'une sphère à 2

$\ quad \ quad a = (\ pi - r_a) / 2$

$\ quad \ quad b = a - \ delta$
Si

$r_a> \ pi$ alors il faut le mettre

$r_a = 2 \ pi - r_a$ et

$\ delta = - \ delta$
Trouvera

$\ vec {OD}$

$\ quad \ quad \ vec {OD} = \ vec {OA} + \ vec {AB} / | \ vec {AB} | \ cdot | \ vec {AD} |$

où

$\ quad \ quad | \ vec {AD} | = | \ vec {AB} | / 2 + | \ vec {OE} |$

$\ quad \ quad | \ vec {OE} | = | \ vec {DE} | / \ tan b$

$\ quad \ quad | \ vec {DE} | = R \ sin a$

va trouver

$\ vec {OC}$

$\ quad \ quad \ vec {OC} = \ vec {OD} / | \ vec {OD} | \ cdot R$

Eclairage

Nous utiliserons deux modèles d'éclairage.

Modèle d'éclairage simple. Dans ce modèle, la luminosité d'un point de surface dépend du cosinus de l'angle entre la normale externe à la surface et la direction de l'observateur. Nous l'utiliserons lors de la construction d'images pour le matériel explicatif. En fait, il s'agit d'un modèle avec une source de lumière ponctuelle située là où se trouve l'observateur, dans laquelle la luminosité d'un point de surface ne dépend pas de la distance à la source lumineuse.

Modèle d'éclairage réaliste. Ce modèle aura une source ponctuelle de lumière dédiée. Nous l'utiliserons pour créer des images réalistes. Ce modèle peut prendre en compte l'influence de la zone du front d'onde sur la luminosité d'un point de surface (en fait, l'influence de la distance à la source lumineuse). Dans un univers fermé à géométrie sphérique, la zone de front d'onde est directement proportionnelle au carré du rayon conditionnel de la sphère avec un rayon géodésique égal à la distance du point de surface à la source lumineuse. Avec la distance de la source de lumière, la zone du front d'onde à l'équateur augmente (les rayons lumineux divergent), et après la diminution de l'équateur (les rayons lumineux convergent, se concentrent). Après avoir passé le point opposé au "centre de l'univers", le processus inverse se produit: les rayons de lumière divergent d'abord, puis convergent à nouveau. De plus, ce modèle peut prendre en compte des particularités de perception ( loi Weber - Fechner ).

Pour construire l'image, nous utiliserons le lancer de rayons inverses . Pour que le modèle soit interactif (nous allons examiner notre monde et nous y déplacer), l'image doit être construite en temps réel. Par conséquent, nous effectuerons les calculs dans le fragment shader (nous utilisons WebGL). Nous implémentons l'interface en JavaScript.

Textures

Texture earth.jpg d'ici

Texture moon.jpg d'ici

Texture sun.png d'ici

Première connaissance

Nous allons créer un monde fermé en trois dimensions avec une longueur de ligne géodésique de 100 - il nous sera donc plus facile de naviguer - l'équateur de notre monde sera situé à une distance de 25 (un quart de la longueur de la ligne géodésique), et le pôle opposé de notre monde - à une distance de 50 (la moitié de la longueur de la ligne géodésique). Nous plaçons une planète dans notre monde et peignons des parties de sa surface en couleurs en fonction de l' octant dans lequel elles tombent:

Octant	Signe X	Signe Y	Signe Z	La couleur
Je	+	+	+	Rouge ( R ed)
II	-	+	+	Vert ( G reen)
III	-	-	+	Bleu ( B lue)
IV	+	-	+	Orange
V	+	+	-	Bleu ( C yan)
VI	-	+	-	Violet ( M agenta)
VII	-	-	-	Jaune (jaune)
VIII	+	-	-	Blanc

Comme texture principale, nous utiliserons la texture d'un échiquier 3x6, c'est-à-dire que chaque parallèle et méridien traversera exactement 12 cellules. Comme texture alternative, nous utiliserons la texture du globe. Voici des photos d'un survol de familiarisation de notre planète.

Un instantané du pôle Nord. L'axe X est dirigé vers la droite, l'axe Y est dirigé vers le haut, l'axe Z est dirigé vers nous. Lors de l'application d'une texture alternative, vous pouvez voir:

à droite, l'océan Pacifique
Ci-dessus - Amérique du Nord
gauche - l'océan Atlantique
en bas - Eurasie

Photos du vol du pôle Nord à l'équateur et de l'équateur au pôle Sud.

Instantané du pôle Sud. L'axe X est dirigé vers la droite, l'axe Y est dirigé vers le bas, l'axe Z est dirigé loin de nous. Lors de l'application d'une texture alternative, vous pouvez voir:

Droite - Océan Pacifique, Nouvelle-Zélande, Australie
d'en haut - Océan Indien
gauche - Océan Atlantique, Afrique
en bas - Amérique du Sud

Étude visuelle

Nous effectuerons une étude visuelle de notre monde afin de découvrir des analogues des effets que nous avons découverts dans un monde fermé à deux dimensions.

Doubles. Comme dans l'analogue bidimensionnel, chaque corps de notre monde aura un double - si nous voyons le pôle Nord devant nous, puis en nous retournant, nous pouvons voir ... le pôle Sud. La contraction de la surface du double est perceptible du fait que nous sommes suffisamment proches de la planète.

Une expérience dans laquelle l'observateur s'éloigne de la planète (le chiffre dans le coin supérieur gauche de chaque image est la distance entre l'observateur et la planète).

On voit que:

initialement la taille angulaire de la planète diminue - c'est la perspective directe habituelle
puis, lorsque la planète a franchi l'équateur de notre monde (distance supérieure à 25), sa taille angulaire augmente - c'est l'effet de la perspective opposée qui nous est familière
en rampant vers le pôle opposé de notre monde, nous voyons une surface rétrécie (distance 46.875)
lorsque la planète est au pôle opposé de notre monde (distance 50) elle s'étire sur tout le ciel
en glissant du pôle opposé de notre monde, nous voyons une surface étirée (distance 53.125)
après que la planète a passé le pôle opposé de notre monde, elle semble transformée symétriquement - l'octant rouge a changé avec le bleu et ainsi de suite
ensuite, la taille angulaire de la planète diminue (distance de 50 à 75), puis augmente (distance de 75 à 100) - c'est l'effet familier des deuxièmes perspectives avant et arrière

Artefacts. Lors de l'utilisation du modèle, il a été remarqué que lors du passage de la planète à travers les points se trouvant à l'observateur à des distances de 25, 50 et 75, des artefacts peuvent apparaître - les cheveux peuvent «pousser» sur la planète ou même s'effriter. Apparemment, mes calculs ne tiennent pas compte de quelque chose)

Une image de la planète à proximité du pôle opposé de notre monde (une «lentille» grand angle a été utilisée). La surface de la planète devant nous est très rétrécie - vous pouvez voir non seulement tout l'hémisphère Nord, mais aussi une partie de l'hémisphère Sud derrière l'équateur. La surface de la planète derrière nous est très étirée - le pôle Sud est bien visible. Les deux surfaces s'étirent l'une vers l'autre, essayant de nous enfermer dans une coquille sphérique et de nous révéler une image d'une planète étirée à travers le ciel.

Une expérience dans laquelle l'observateur lève les yeux (le nombre dans le coin supérieur gauche de chaque image est l'angle entre la direction descendante et le regard).

En images:

apparaît d'abord l'horizon de notre côté de la planète
puis, nous voyons un deuxième horizon au-dessus, où nous trouvons ce qui est situé de notre côté de la planète derrière notre dos derrière l'horizon
levant les yeux, nous voyons le dos de la planète

Image à double horizon («objectif» grand angle utilisé). La bande du ciel est suffisamment grande car nous sommes à une altitude d'environ 50 km.

Une image du ciel au-dessus de la tête (un «objectif» grand angle a été utilisé).

Un monde sans nuit.
De plus, pour simplifier, nous appellerons notre planète Terre, son satellite naturel - la Lune et l'étoile autour de laquelle ils tournent - le Soleil. Les proportions des tailles du Soleil, de la Terre, de la Lune et de leurs orbites pour plus de clarté ne seront pas observées.
Sur la photo: la frontière entre les côtés jour et nuit de la planète traversant l'océan Atlantique. Dans le même temps, la Terre décroissante et croissante est visible. Les gars assis sur les bases lunaires de notre monde voient une image à peu près similaire)

Sur l'animation: le mouvement de la frontière entre les côtés jour et nuit de la Terre. Vous pouvez voir le chevauchement du Soleil par le disque de la Terre illuminé par les rayons du Soleil libérés le long d'un long chemin.

Éclipses solaires et lunaires.
Sur la photo: la lune émerge de l'ombre de la Terre. Les frontières entre les côtés jour et nuit de la Terre et de la Lune sont visibles.

En animation: éclipses solaires et lunaires.

On voit que:

tout d'abord, la terre jette une ombre sur la lune, et la lune jette une ombre sur la terre
alors la lune sort de l'ombre de la terre, et l'ombre de la lune quitte la surface de la terre
puis l'ombre de la lune revient à la surface de la terre et la lune pénètre à nouveau dans l'ombre de la terre
la frontière entre les côtés jour et nuit de la lune n'est pas visible lorsque la lune est recouverte par le disque de la Terre car le côté de la lune qui nous fait face est toujours dans l'ombre de la Terre

Sur l'animation: le mouvement des frontières entre les côtés jour et nuit de la Terre et de la Lune combiné aux éclipses solaires et lunaires. Les gars qui servent les observatoires du point L _{2 de} Lagrange dans notre monde voient à peu près la même image) Bien sûr, si nous négligeons la rotation de la Terre)

Sur la photo: l'aube sur l' ISS dans notre monde)

Conclusion

À quoi ça sert)? Je voulais juste vraiment voir le monde à travers les yeux d'une créature vivant dans un univers fermé compact avec une géométrie sphérique. Connaître ce monde merveilleux sans les symboles de Christoffel et autres choses similaires tout en restant dans le cadre du cours général de mathématiques supérieures. Le résultat est devant vous. Tout semble fonctionner. J'espère que vous avez passé une journée intéressante et agréable!

Code source .

Modèle fonctionnel (ouvert sur PC, pas pour les appareils mobiles).

Pour ceux qui s'intéressent au sujet, il y a un magnifique article qui parle des phénomènes étonnants qui peuvent être observés dans le vrai univers: Comment dessiner un trou noir. Traçage de rayons géodésiques dans l'espace-temps incurvé .

Le monde de l'hypersphère tridimensionnelle. Traçage de rayons géodésiques dans un univers fermé à géométrie sphérique

Présentation Monde fermé à deux dimensions

Monde clos tridimensionnel

Modèle

Première connaissance

Étude visuelle

Conclusion

More articles: