Logistique de l'action pour la collecte sélective des matières recyclables

Au lieu de rejoindre

Lorsque les processus de collecte et de traitement des déchets sont entièrement ajustés en Russie, ce n'est pas facile à dire, mais je ne veux pas participer à la reconstitution des décharges maintenant. Par conséquent, dans de nombreuses grandes villes, d'une manière ou d'une autre, il existe des mouvements de volontaires engagés dans une collecte séparée particulière.

À Novossibirsk, une telle activité se forme autour de la campagne Green Squirrel, dans le cadre de laquelle une fois par mois, les citadins soucieux de l'environnement apportent à un certain moment des déchets ménagers recyclables accumulés vers des lieux prédéterminés. En même temps, un camion loué arrive sur place, qui emmène les matières recyclables collectées et triées sur le site, d'où il est redistribué entre les différentes entreprises de transformation. L'action existe depuis 2014, et depuis lors, le nombre de points de collecte pour les matières recyclables, ainsi que ses volumes, a considérablement augmenté. Pour le routage des camions, un simple regard ne suffisait pas et nous avons commencé à développer des modèles d'optimisation pour minimiser les coûts de transport. Le premier de ces modèles fait l'objet de cet article.

Dans la section 1, je décrirai en détail et avec des illustrations le schéma d'organisation de l'action. En outre, dans la section 2, la tâche de minimiser les coûts de transport sera formalisée comme la tâche de routage des véhicules hétérogènes problème de routage des véhicules de la flotte avec des fenêtres de temps. La section 3 est consacrée à la résolution de ce problème à l'aide d'un package librement distribué pour résoudre les problèmes de programmation mathématique linéaire à nombres entiers mixtes GLPK.

1. L'action "Ecureuil vert"

Depuis 2014, le groupe d'initiative Living Earth mène une campagne mensuelle pour séparer la collecte d' écureuil vert recyclé à Novossibirsk. Au moment de la rédaction du présent document, le recyclage avec un certain nombre de réserves est accepté comme déchet plastique étiqueté PET, PE, PP, PS, verre, aluminium, fer, appareils électroménagers, vieux papiers et plus encore. Plus de 50 bénévoles participent à la préparation et à la conduite de l'action. L'action n'est pas commerciale, sa participation est gratuite et n'implique pas de récompense monétaire.

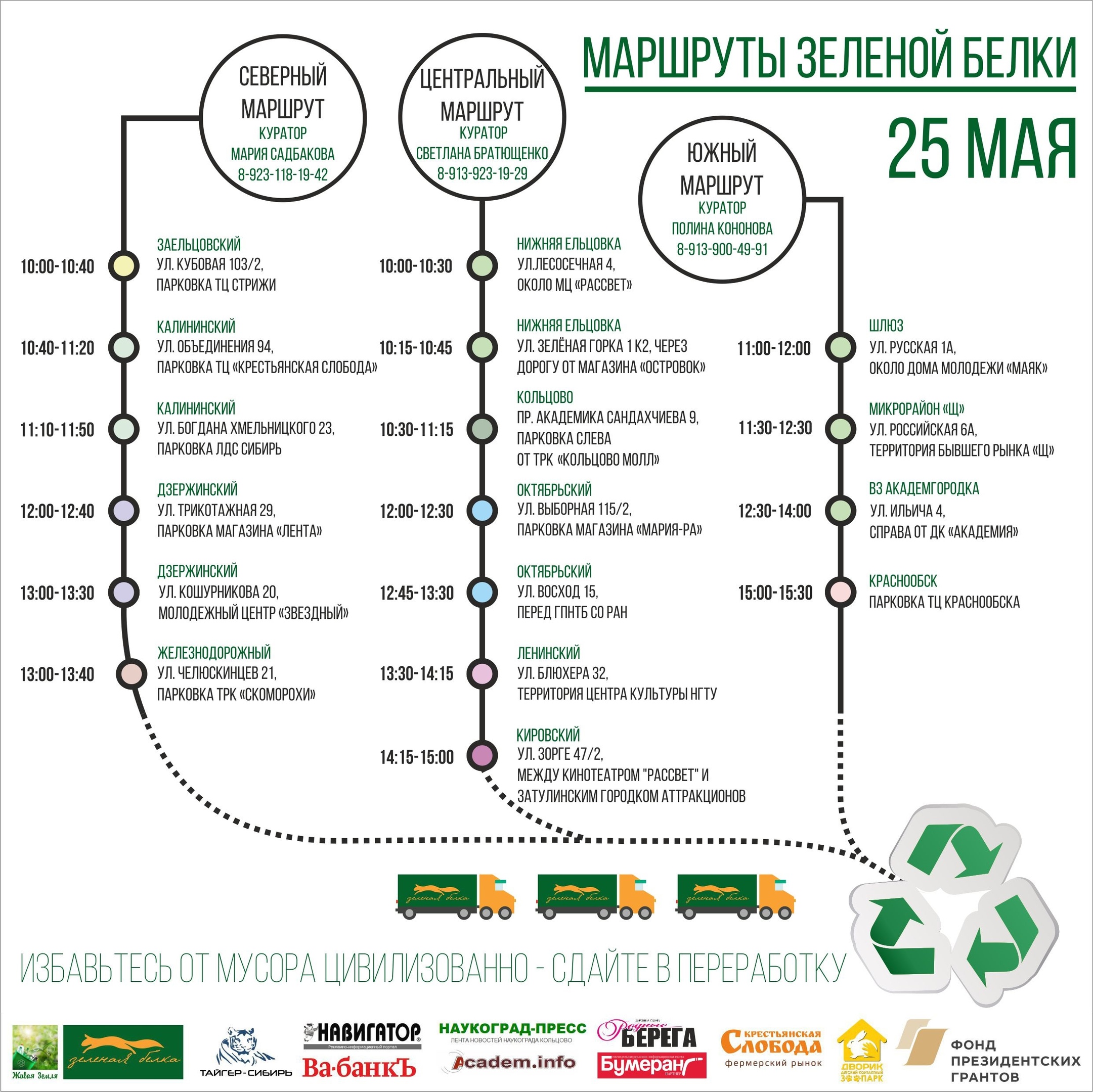
Des points

L'action se déroule à 17 points de la ville, situés les uns des autres à des distances couvertes par la voiture dans une période de 15 à 90 minutes. Un de ces points sur la photo: des sacs à gauche le long du mur pour collecter diverses fractions de plastique, à droite - un camion, dans lequel tout est chargé à l'avenir, et au centre - un volontaire avec des oreilles.



Toutes les activités au point sont organisées par des conservateurs qui ont des restrictions sur le moment où ils sont prêts à remplir leurs fonctions. Lors de la planification d'une action, les conservateurs signalent l'intervalle de temps pendant lequel l'action doit se terminer à leur point.

Il existe également des données sur les volumes moyens de matières recyclables collectées à chaque point.

Itinéraires

Les points sont organisés en parcours successivement conduits par un camion. Les mouvements des camions sont surveillés par des superviseurs d'itinéraire qui surveillent l'environnement opérationnel et prennent des décisions sur la gestion des événements spéciaux.



Camions

Sont loués sur une base commune dans le cadre de propositions de location horaire de véhicules de fret. Il n'est pas possible de compacter le plastique en place, donc le paramètre principal caractérisant le camion est le volume de la caisse. La capacité de charge dans notre cas n'est pas un facteur limitant.

Les principales dépenses de l'action sont liées au paiement de la location de camions, donc sa réduction est critique pour l'existence et le développement de notre part, qui acquiert une signification institutionnelle dans le sens de former des idées sur la consommation responsable. Ensuite, une approche pour résoudre ce problème sera décrite, basée sur l'application de méthodes d'optimisation discrètes, à savoir la programmation mathématique.

2. Formalisation

Dans la construction du modèle mathématique, nous resterons dans le cadre de programmes linéaires à nombres mixtes, pour lesquels la connaissance de l'algèbre de classe 7 est suffisante.

La seule difficulté peut être associée à l'utilisation de la notation abstraite et des signes de sommation dans les formules. J'espère que cela n'effraie pas les lecteurs qui ont des rencontres peu fréquentes avec des textes mathématiques.

Dans le modèle d'optimisation, quatre composants peuvent être distingués:

• la formation de groupes de points qui composent un itinéraire distinct;
• définition d'un plan de détour pour chacun des groupes;
• répondre aux exigences relatives à l'heure d'arrivée du camion à chaque point;
• détermination du type de camion nécessaire pour desservir chacun des itinéraires.

Nous considérons chacune des parties, en introduisant la notation nécessaire si nécessaire.

Regroupement de points

Soit $$$V = \ {1, \ dots, n \}$ il existe de nombreux indices de points de collecte pour les matières recyclables, et le site où les matières recyclables collectées sont ensuite transportées - nous l'appellerons un dépôt - a un indice de 0. $$$\ bar {V} = V \ cup \ {0 \}$

Chaque groupe de points forme un itinéraire distinct. À travers $$$R$ désignent l'ensemble des numéros de route.

Laissez la quantité $$$z_ {ir}, i \ in I, r \ in R$ est égal à un si le point $$$i$ inclus dans l'itinéraire avec le numéro $$$r$ et zéro sinon. Ensuite, l'exigence que le point $$$i \ in V$ doit entrer l'un des itinéraires peut être écrit comme

$$

$$\ sum_ {r \ in R} z_ {ir} = z_ {i1} + z_ {i2} + \ dots + z_ {in} = 1.$$

Le dépôt doit saisir toutes les routes: $$$z_ {0r} = 1, r \ in R$


Définition d'un détour

Les itinéraires sont une séquence alternée de points et de croisements entre eux. Formellement, ils commencent tous à l'un des points de l'ensemble $$$V$ et se terminent au dépôt, cependant, il sera plus facile de supposer que toutes les routes sont cycliques. Cette hypothèse ne change pas l'essence, mais rend tous les sommets identiques: dans ce cas, il n'y a pas de sommets d'extrémité, ils sont tous en transit.

Pour les points $$$i, j \ in \ bar {V}$ et itinéraire $$$r \ in R$ configurer une variable $$$x_ {ijr}$ égal à un si dans l'itinéraire avec un numéro $$$r$ camion se déplaçant du point $$$i$ au point $$$j$ et zéro sinon.

Ensuite, nous exigeons, premièrement, que le camion se déplaçant le long de l'itinéraire $$$r \ in R$ visité le point $$$i \ in V$ si elle, après avoir divisé en groupes, est tombée dans le groupe avec le nombre $$$r$ :

$$

$$\ sum_ {j \ in \ bar {V}} x_ {jir} = z_ {ir}, \ quad i \ in \ bar {V}, r \ in R.$$

Deuxièmement, le camion après son arrivée au point $$$i \ in \ bar {V}$ doit la quitter.

$$

$$\ sum_ {j \ in \ bar {V}} x_ {jir} = \ sum_ {j \ in \ bar {V}} x_ {ijr}, \ quad i \ in \ bar {V}, r \ in R .$$

Vous remarquerez peut-être que ces restrictions autorisent les quantités $$$x_ {ijr}$ Définissez des routes qui sont un ensemble de boucles disjointes. Les itinéraires de ce type n'ont bien entendu aucun sens et un certain nombre de restrictions sont nécessaires pour éviter cela.


Satisfaire aux exigences au moment de l'arrivée du camion à chaque point

En d'autres termes, vous devez visiter les points uniquement à l'intérieur des fenêtres temporelles indiquées par les conservateurs. À travers $$$B_i$ et $$$E_i$ indiquent respectivement le début et la fin de l'intervalle de temps dans lequel le conservateur du point $$$i$ peut y assister.

Pour suivre la mise en œuvre de ces restrictions, nous avons besoin d'informations sur le temps passé par le camion lors des arrêts et des traversées sur l'itinéraire. À travers $$$L_i, i \ in V$ désigne la durée du chargement au point $$$i$ , et par $$$D_ {ij}, i, j \ in \ bar {V}$ - le temps de se déplacer d'un point $$$i$ au point $$$j$ Nous faisons une réservation $$$D_ {0i} = 0$ pour tous $$$i \ in \ bar {V}$ , et peut généralement être effectuée $$$D_ {ij} \ neq D_ {ji}$ pour tout $$$i \ neq j$

Nous introduisons des variables non négatives $$$a_i, i \ in \ bar {V}$ et $$$w_ {ir}, i \ in \ bar {V}, r \ in R$ égal aux heures d'arrivée et aux temps d'attente au point $$$i$ lors de la conduite sur un itinéraire $$$r$ , respectivement. Pour les valeurs saisies, les relations suivantes doivent être satisfaites.

Le temps d'attente ne peut être inférieur au temps de chargement

$$

$$w_ {ir} \ geq L_iz_ {ir}, \ quad i \ in \ bar {V}, r \ in R,$$

et égal à zéro si le point n'appartient pas à l'itinéraire $$$r$

$$

$$w_ {ir} \ leq Mz_ {ir}, \ quad i \ in \ bar {V}, r \ in R,$$

Heure d'arrivée au point $$$j$ calculé aux moments appropriés pour le point précédent $$$i$ Voici une constante assez grande $$$M$ utilisé pour éliminer les dépendances inutiles lors du déplacement entre $$$i$ et $$$j$ pas fait.

$$

$$a_i + \ sum_ {r \ in R} w_ {ir} + D_ {ij} \ leq a_j + M (1 - \ sum_ {r \ in R} x_ {ijr}), \ quad i \ in I, j \ en V,$$

L'arrivée et le départ du camion doivent se faire dans l'intervalle indiqué par le conservateur.

$$

$$a_i \ geq B_i, \ quad i \ in V,$$

$$

$$a_i + \ sum_ {r \ in R} w_ {ir} \ leq E_i, \ quad i \ in V.$$

Déterminer le type de camion nécessaire pour desservir chaque itinéraire
Indique les nombreux types de camions disponibles à la location par $$$T$ Type de camion $$$t \ in T$ caractérisé par le volume corporel $$$C_t$ et le coût d'une heure de loyer $$$P_t$ Temps minimum de location de camion $$$t$ dénoter par $$$U_t ^ 0$ La quantité de matières recyclables collectées au point $$$i \ in V$ dénoter par $$$G_i$

Nous introduisons des variables $$$y_ {tr}, t \ dans T, r \ dans R$ égal à un si type de camion $$$t$ affecté à l'itinéraire de service avec un numéro $$$r$ et zéro sinon.

Variables entières $$$u_ {tr}, t \ in T, r \ in R$ définir l'heure de location d'un type de camion $$$t$ desservant l'itinéraire avec un numéro $$$r$
Pour chaque itinéraire, $$$r \ in R$ , vous devez attribuer le type de camion:

$$

$$\ sum_ {t \ in T} y_ {tr} = 1, \ quad r \ in R$$

Conformément à la répartition des points entre les itinéraires, certains itinéraires peuvent se révéler triviaux, c'est-à-dire ne contenir que des dépôts. Si l'itinéraire $$$r$ non triviale, le camion qui lui est affecté est loué au moins $$$U_t ^ 0$ heures.

$$

$$u_ {tr} \ geq U_t ^ 0 (y_ {tr} - \ sum_ {i \ in V} z_ {ir}), \ quad t \ in T, r \ in R.$$

Dans le même temps, la durée du bail devrait également dépasser la durée totale de stationnement et de déplacement le long du parcours.

$$

$$u_ {tr} \ geq \ sum_ {i \ in V} \ sum_ {j \ in \ bar {V}} D_ {ij} x_ {ijr} + \ sum_ {i \ in \ bar {V}} w_ { ir} -M (1-y_ {tr}), \ quad r \ in R, t \ in T.$$

Ajouter des restrictions fournissant la propriété: si le camion est de type $$$t$ non affecté à un itinéraire $$$r$ , son temps de location est nul.

$$

$$u_ {tr} \ leq My_ {tr}.$$

Tous les produits recyclables collectés aux points de passage doivent tenir à l'arrière du camion.

$$

$$\ sum_ {i \ in V} G_iz_ {ir} \ leq \ sum_ {t \ in T} C_ty_ {tr}, \ quad r \ in R.$$

Enfin, notre objectif est de minimiser le coût de la location de camions, qui, en utilisant les désignations introduites, s'écrit $$$\ sum_ {t \ in T} \ sum_ {r \ in R} P_tu_ {tr}$

Rechercher une solution

Il est facile de vérifier que toutes les expressions impliquées dans le modèle d'optimisation sont des fonctions linéaires de variables.Par conséquent, pour trouver des solutions exactes et approximatives, vous pouvez utiliser des packages standard pour résoudre des problèmes de programmation en nombres mixtes tels que Gurobi , CPLEX , Xpress , ORtools , SCIP , BLIS , etc.
Nous écrivons un modèle pour minimiser les coûts de transport dans le langage GMPL. Cela nous permettra d'utiliser le package GLPK gratuit à nos fins. Pour écrire du code et déboguer le modèle, il sera pratique de télécharger l' environnement de développement GUSEK , qui contient déjà GLPK dans sa composition.

GUSEK ressemble à ceci:



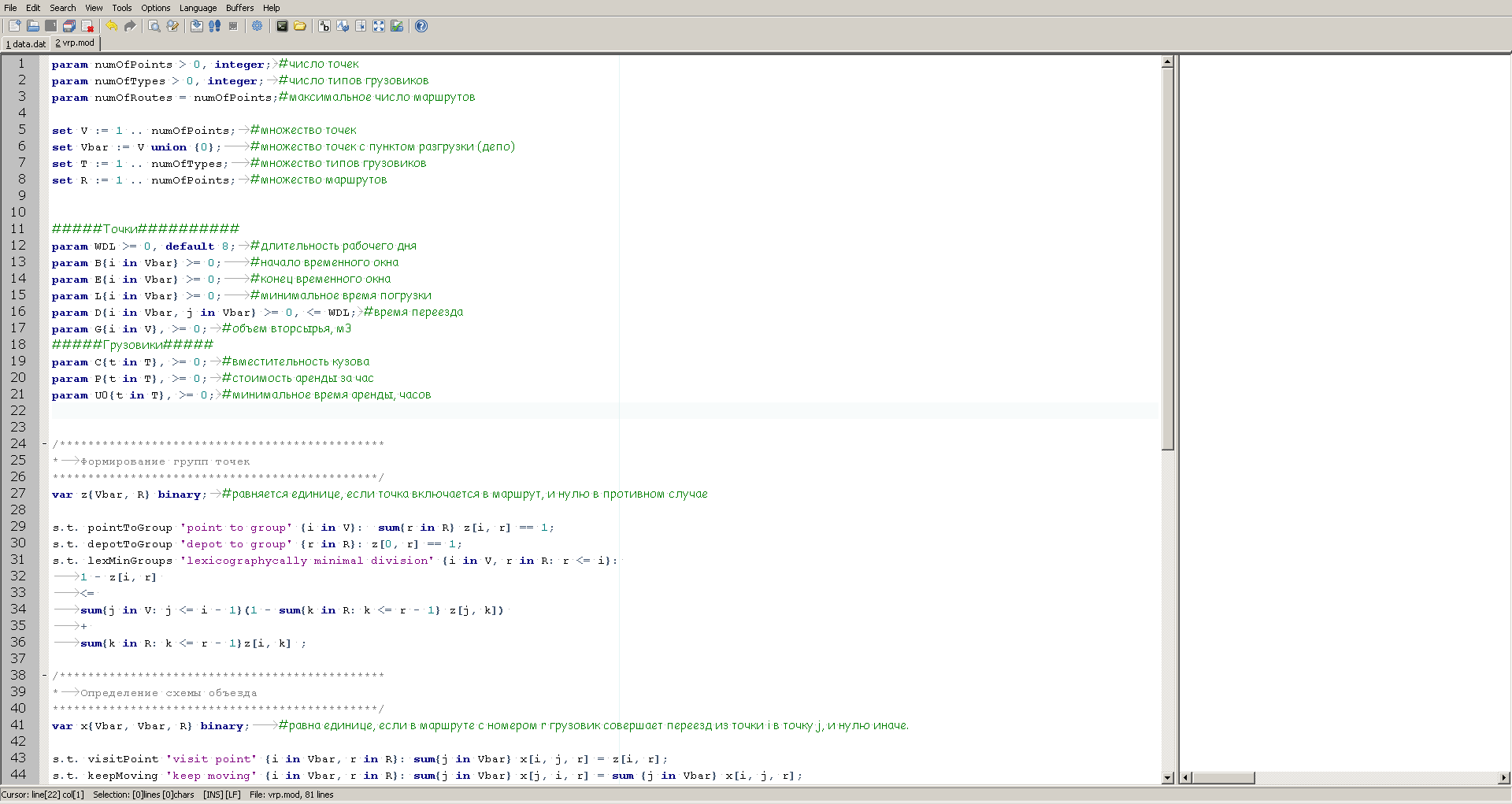
Sur la gauche, nous voyons une description du modèle, et sur la droite, il y a une fenêtre pour afficher des informations sur la progression du calcul, que le solveur fournira après le lancement.


Pour un démarrage rapide, j'ajouterai également des données provenant de ma tête préparées pour être utilisées dans le modèle:


Après avoir copié le code du modèle dans un fichier portant le nom, par exemple, model.mod et les données d'entrée dans le fichier data.dat, tout est prêt à fonctionner. Nous fixons une limite au temps de calcul de 100 secondes (cela se fait en utilisant la clé --tmlim [temps en secondes]), transférons le chemin vers le fichier avec les données d'entrée (en utilisant la clé -d [chemin du fichier]),



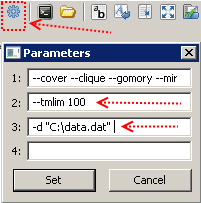
et appuyez sur F5. En cas de succès, des messages apparaîtront dans la fenêtre de droite, et après une centaine de secondes, nous aurons la meilleure solution que GLPK a réussi à trouver dans le temps imparti.



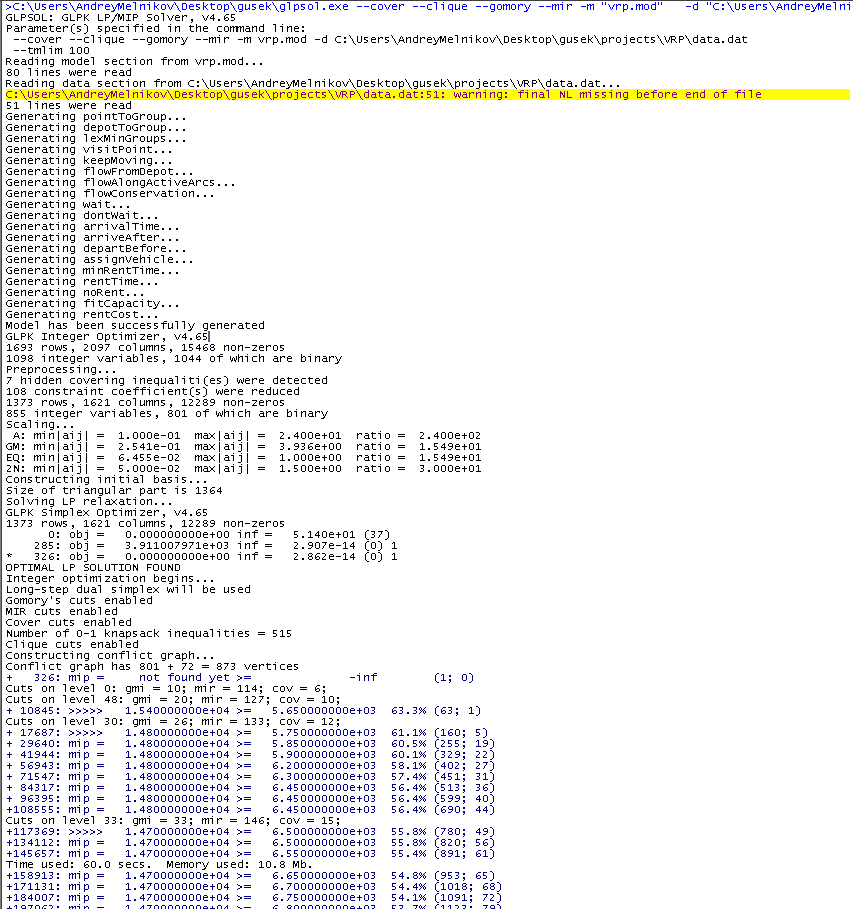
Dans le texte bleu, nous nous intéressons au sens après l'inscription "mip =". Comme vous pouvez le voir, il diminue de temps en temps. Toutes les nouvelles solutions sont en cours de réalisation, dont la valeur des frais de transport au mieux est affichée dans cette colonne (il y en a 14700 à ce jour). Le nombre suivant est la borne inférieure de la meilleure solution existante, c'est-à-dire optimale . Initialement, l'estimation est considérablement sous-estimée, mais elle s'affine avec le temps, c'est-à-dire qu'elle augmente. Les valeurs de gauche et de droite convergent et l'écart relatif entre elles au moment de la capture d'écran est de 54,1%. Dès que ce nombre devient nul, l'algorithme prouvera que la meilleure solution trouvée est la meilleure possible. Il n'est pas toujours justifié d'attendre cet événement dans la pratique, et pas seulement parce que c'est long, mais il est important de faire une réservation qui, en règle générale, une bonne solution est relativement rapide, et les principaux coûts de temps sont associés au raffinement de l'estimation nécessaire pour prouver le meilleur possible.

Au lieu d'une conclusion

Les problèmes de routage sont extrêmement complexes sur le plan informatique et avec l'augmentation du nombre de points à visiter, le temps nécessaire à un solveur pour trouver une solution et prouver que son optimalité augmente rapidement. Cependant, pour des exemples assez petits, dans un laps de temps raisonnable, le solveur est capable de créer un ensemble de routes réussi et peut être utilisé pour prendre des décisions. L'analyse des options de routage proposées par le modèle nous a permis de découvrir des opportunités importantes de réduction des coûts, ce qui est critique pour l'existence et le développement du stock.

Nos efforts se sont poursuivis pour travailler avec une incertitude sur les volumes de matières recyclables collectées aux points. Nous développons un certain nombre de modèles de programmation stochastiques pour prendre des décisions stratégiques et opérationnelles dans l'acheminement des camions. Si le sujet s'avère pertinent et suscite de l'intérêt, j'écrirai également à ce sujet, car bientôt nous devrons tous approfondir de manière beaucoup plus approfondie les questions environnementales, ce dans quoi je souhaite que nous réussissions.