Réseaux de neurones et apprentissage profond, chapitre 1: utiliser les réseaux de neurones pour reconnaître les nombres manuscrits

Remarque

Voici une traduction du livre en ligne gratuit de Michael Nielsen Neural Networks and Deep Learning, distribué sous la licence Creative Commons Attribution-NonCommercial 3.0 Unported . La motivation de sa création a été l'expérience réussie de la traduction d'un manuel de programmation, Expressive JavaScript . Le livre sur les réseaux de neurones est également très populaire; les auteurs d'articles en anglais le citent activement. Je n'ai pas trouvé ses traductions, à l'exception de la traduction du début du premier chapitre avec des abréviations .

Ceux qui souhaitent remercier l'auteur du livre peuvent le faire sur sa page officielle , par virement via PayPal ou Bitcoin. Pour soutenir le traducteur sur Habré, il existe un formulaire "pour soutenir l'auteur".

Présentation

Ce tutoriel vous expliquera en détail des concepts tels que:

• Réseaux de neurones - un excellent paradigme logiciel, créé sous l'influence de la biologie, et permettant à l'ordinateur d'apprendre sur la base des observations.
• L'apprentissage en profondeur est un ensemble puissant de techniques de formation aux réseaux de neurones.

Les réseaux de neurones (NS) et l'apprentissage profond (GO) offrent aujourd'hui la meilleure solution à de nombreux problèmes dans les domaines de la reconnaissance d'image, du traitement de la voix et du langage naturel. Ce didacticiel vous apprendra bon nombre des concepts clés qui sous-tendent NS et GO.

De quoi parle ce livre

NS est l'un des plus beaux paradigmes logiciels jamais inventés par l'homme. Avec une approche de programmation standard, nous disons à l'ordinateur ce qu'il faut faire, divisons les grandes tâches en plusieurs petites et déterminons précisément les tâches que l'ordinateur effectuera facilement. Dans le cas de l'Assemblée nationale, au contraire, nous ne disons pas à l'ordinateur comment résoudre le problème. Il l'apprend lui-même sur la base «d'observations» des données, «inventant» sa propre solution au problème.

L'apprentissage automatisé basé sur les données semble prometteur. Cependant, jusqu'en 2006, nous ne savions pas comment former l'Assemblée nationale pour qu'elle puisse dépasser les approches plus traditionnelles, à l'exception de quelques cas particuliers. En 2006, les techniques de formation des soi-disant réseaux de neurones profonds (GNS). Maintenant, ces techniques sont connues sous le nom d'apprentissage profond (GO). Ils ont continué à être développés et, aujourd'hui, GNS et GO ont obtenu des résultats étonnants dans de nombreuses tâches importantes liées à la vision par ordinateur, à la reconnaissance vocale et au traitement du langage naturel. À grande échelle, ils sont déployés par des sociétés telles que Google, Microsoft et Facebook.

Le but de ce livre est de vous aider à maîtriser les concepts clés des réseaux de neurones, y compris les techniques modernes de GO. Après avoir travaillé avec le didacticiel, vous écrirez un code qui utilise NS et GO pour résoudre des problèmes complexes de reconnaissance de formes. Vous aurez une base pour utiliser NS et la protection civile dans l'approche de la résolution de vos propres problèmes.

Approche basée sur des principes

L'une des croyances qui sous-tendent le livre est qu'il vaut mieux acquérir une solide compréhension des principes clés de l'Assemblée nationale et de la société civile que de tirer les connaissances d'une longue liste d'idées différentes. Si vous avez une bonne compréhension des idées clés, vous comprendrez rapidement d'autres nouveaux éléments. Dans le langage du programmeur, nous pouvons dire que nous étudierons la syntaxe de base, les bibliothèques et les structures de données du nouveau langage. Vous pouvez reconnaître seulement une petite fraction de la langue entière - de nombreuses langues ont d'immenses bibliothèques standard - cependant, vous pouvez comprendre de nouvelles bibliothèques et structures de données rapidement et facilement.

Donc, ce livre n'est catégoriquement pas du matériel éducatif sur la façon d'utiliser une bibliothèque particulière pour l'Assemblée nationale. Si vous voulez simplement apprendre à travailler avec la bibliothèque - ne lisez pas le livre! Trouvez la bibliothèque dont vous avez besoin et travaillez avec du matériel de formation et de la documentation. Mais gardez à l'esprit: bien que cette approche ait l'avantage de résoudre instantanément le problème, si vous voulez comprendre ce qui se passe exactement à l'Assemblée nationale, si vous voulez maîtriser des idées qui seront pertinentes dans de nombreuses années, alors il ne vous suffira pas d'étudier simplement une sorte de bibliothèque de mode. Vous devez comprendre les idées fiables et à long terme qui sous-tendent le travail de l'Assemblée nationale. La technologie va et vient, et les idées durent pour toujours.

Approche pratique

Nous étudierons les principes de base par l'exemple d'une tâche spécifique: apprendre à un ordinateur à reconnaître les nombres manuscrits. En utilisant des approches de programmation traditionnelles, cette tâche est extrêmement difficile à résoudre. Cependant, nous pouvons le résoudre assez bien avec un simple NS et plusieurs dizaines de lignes de code, sans bibliothèques spéciales. De plus, nous améliorerons progressivement ce programme, en y incluant de plus en plus d'idées clés sur l'Assemblée nationale et la défense civile.

Cette approche pratique signifie que vous aurez besoin d'une certaine expérience en programmation. Mais vous n'avez pas besoin d'être un programmeur professionnel. J'ai écrit du code python (version 2.7) qui devrait être clair même si vous n'avez pas écrit de programmes python. En cours d'étude, nous créerons notre propre bibliothèque pour l'Assemblée nationale, que vous pourrez utiliser pour des expériences et une formation continue. Tout le code peut être téléchargé ici . Après avoir terminé le livre, ou en cours de lecture, vous pouvez choisir l'une des bibliothèques les plus complètes pour l'Assemblée nationale, adaptée pour être utilisée dans ces projets.

Les exigences mathématiques pour comprendre le matériau sont assez moyennes. La plupart des chapitres ont des parties mathématiques, mais généralement ce sont des graphes d'algèbre élémentaire et de fonction. Parfois, j'utilise des mathématiques plus avancées, mais j'ai structuré le matériel pour que vous puissiez le comprendre, même si certains détails vous échappent. La plupart des mathématiques sont utilisées dans le chapitre 2, qui nécessite un peu de matanalyse et d'algèbre linéaire. Pour ceux à qui ils ne sont pas familiers, je commence le chapitre 2 par une introduction aux mathématiques. Si vous trouvez cela difficile, sautez simplement le chapitre jusqu'au débriefing. Dans tous les cas, ne vous en faites pas.

Un livre est rarement à la fois orienté vers une compréhension des principes et une approche pratique. Mais je pense qu'il vaut mieux étudier sur la base des idées fondamentales de l'Assemblée nationale. Nous allons écrire du code de travail, et pas seulement étudier la théorie abstraite, et vous pouvez explorer et étendre ce code. De cette façon, vous comprendrez les bases, à la fois la théorie et la pratique, et serez en mesure d'apprendre davantage.

Exercices et tâches

Les auteurs de livres techniques avertissent souvent le lecteur qu'il a simplement besoin de terminer tous les exercices et de résoudre tous les problèmes. En me lisant de tels avertissements, ils semblent toujours un peu étranges. Est-ce que quelque chose de mauvais m'arrivera si je n'exécute pas les exercices et ne résout pas les problèmes? Non, bien sûr. Je gagnerai juste du temps en comprenant moins profondément. Parfois ça vaut le coup. Parfois non.

Que vaut-il la peine de faire avec ce livre? Je vous conseille d'essayer de terminer la plupart des exercices, mais n'essayez pas de résoudre la plupart des tâches.

La plupart des exercices doivent être complétés car ce sont des vérifications de base pour une bonne compréhension du matériel. Si vous ne pouvez pas effectuer l'exercice avec une relative facilité, vous devez avoir raté quelque chose de fondamental. Bien sûr, si vous êtes vraiment coincé dans une sorte d'exercice - laissez tomber, c'est peut-être une sorte de petit malentendu, ou peut-être que j'ai mal formulé quelque chose. Mais si la plupart des exercices vous posent des problèmes, vous devrez probablement relire le matériel précédent.

Les tâches sont une autre affaire. Ils sont plus difficiles que les exercices, et avec certains, vous aurez du mal. C'est ennuyeux, mais bien sûr, la patience face à une telle déception est le seul moyen de vraiment comprendre et absorber le sujet.

Je ne recommande donc pas de résoudre tous les problèmes. Mieux encore - choisissez votre propre projet. Vous voudrez peut-être utiliser NS pour classer votre collection de musique. Ou pour prédire la valeur des stocks. Ou autre chose. Mais trouvez un projet intéressant pour vous. Et puis, vous pouvez ignorer les tâches du livre ou les utiliser uniquement comme source d'inspiration pour travailler sur votre projet. Les problèmes avec votre propre projet vous apprendront plus que de travailler avec un certain nombre de tâches. L'implication émotionnelle est un facteur clé dans la réussite de la maîtrise.

Bien sûr, même si vous n'avez pas un tel projet. C'est normal. Résolvez des tâches pour lesquelles vous ressentez une motivation intrinsèque. Utilisez le matériel du livre pour vous aider à trouver des idées de projets créatifs personnels.

Chapitre 1

Le système visuel humain est l'une des merveilles du monde. Considérez la séquence suivante de nombres manuscrits:



La plupart des gens les liront facilement, comme 504192. Mais cette simplicité est trompeuse. Dans chaque hémisphère du cerveau, une personne a un cortex visuel primaire , également connu sous le nom de V1, qui contient 140 millions de neurones et des dizaines de milliards de connexions entre eux. Dans le même temps, non seulement V1 est impliqué dans la vision humaine, mais toute une séquence de régions cérébrales - V2, V3, V4 et V5 - qui sont engagées dans un traitement d'image de plus en plus complexe. Nous portons dans nos têtes un supercalculateur à l'écoute de l'évolution depuis des centaines de millions d'années, et parfaitement adapté pour comprendre le monde visible. Reconnaître des nombres manuscrits n'est pas si facile. C'est juste que nous, les gens, étonnamment, étonnamment bien, reconnaissons ce que nos yeux nous montrent. Mais presque tout ce travail est effectué inconsciemment. Et généralement, nous n'accordons pas d'importance à la tâche difficile que nos systèmes visuels résolvent.

La difficulté de reconnaître les modèles visuels devient apparente lorsque vous essayez d'écrire un programme informatique pour reconnaître des nombres comme ceux ci-dessus. Ce qui semble facile dans notre exécution se révèle soudain extrêmement complexe. Le concept simple de la façon dont nous reconnaissons les formes - «le neuf a une boucle en haut et la barre verticale en bas à droite» - n'est pas du tout aussi simple pour une expression algorithmique. En essayant d'articuler clairement ces règles, vous vous retrouvez rapidement coincé dans un bourbier d'exceptions, d'embûches et d'occasions spéciales. La tâche semble désespérée.

Approche NS pour résoudre le problème d'une manière différente. L'idée est de prendre les nombreux nombres manuscrits connus comme exemples d'enseignement,



et développer un système qui peut apprendre de ces exemples. En d'autres termes, l'Assemblée nationale utilise des exemples pour construire automatiquement des règles de reconnaissance des chiffres manuscrites. De plus, en augmentant le nombre d'exemples de formation, le réseau peut en apprendre davantage sur les nombres manuscrits et améliorer sa précision. Ainsi, bien que je n'ai cité que 100 études de cas, nous pouvons peut-être créer un meilleur système de reconnaissance de l'écriture manuscrite en utilisant des milliers, voire des millions et des milliards d'études de cas.

Dans ce chapitre, nous allons écrire un programme informatique qui implémente l'apprentissage NS pour reconnaître les nombres manuscrits. Le programme ne comptera que 74 lignes et n'utilisera pas de bibliothèques spéciales pour l'Assemblée nationale. Cependant, ce programme court sera capable de reconnaître des nombres manuscrits avec une précision de plus de 96%, sans nécessiter d'intervention humaine. De plus, dans les prochains chapitres, nous développerons des idées qui peuvent améliorer la précision à 99% ou plus. En fait, les meilleures NS commerciales font un si bon travail qu'elles sont utilisées par les banques pour traiter les chèques et le service postal pour reconnaître les adresses.

Nous nous concentrons sur la reconnaissance de l'écriture manuscrite, car il s'agit d'un excellent prototype de tâche pour étudier la NS. Un tel prototype est idéal pour nous: c'est une tâche difficile (reconnaître les nombres manuscrits n'est pas une tâche facile), mais pas si compliqué qu'il nécessite une solution extrêmement complexe ou une immense puissance de calcul. De plus, c'est un excellent moyen de développer des techniques plus complexes, telles que GO. Par conséquent, dans le livre, nous reviendrons constamment sur la tâche de reconnaissance de l'écriture manuscrite. Plus tard, nous verrons comment ces idées peuvent être appliquées à d'autres tâches de vision par ordinateur, à la reconnaissance vocale, au traitement du langage naturel et à d'autres domaines.

Bien sûr, si le but de ce chapitre était seulement d'écrire un programme pour reconnaître les nombres manuscrits, alors le chapitre serait beaucoup plus court! Cependant, dans le processus, nous développerons de nombreuses idées clés liées à la NS, y compris deux types importants de neurones artificiels ( perceptron et neurone sigmoïde), et l'algorithme d'apprentissage NS standard, la descente de gradient stochastique . Dans le texte, je me concentre à expliquer pourquoi tout est fait de cette façon et à façonner votre compréhension de l'Assemblée nationale. Cela nécessite une conversation plus longue que si je venais de présenter les mécanismes de base de ce qui se passe, mais cela coûte une compréhension plus profonde que vous aurez. Entre autres avantages - à la fin du chapitre, vous comprendrez ce qu'est une protection civile et pourquoi elle est si importante.

Perceptrons

Qu'est-ce qu'un réseau neuronal? Pour commencer, je vais parler d'un type de neurone artificiel appelé le perceptron. Les perceptrons ont été inventés par le scientifique Frank Rosenblatt dans les années 50 et 60, inspirés des premiers travaux de Warren McCallock et Walter Pitts . Aujourd'hui, d'autres modèles de neurones artificiels sont utilisés plus souvent - dans ce livre, et la plupart des travaux modernes sur NS utilisent principalement le modèle sigmoïde du neurone. Nous la rencontrerons bientôt. Mais pour comprendre pourquoi les neurones sigmoïdes sont définis de cette manière, il vaut la peine de passer du temps à analyser le perceptron.

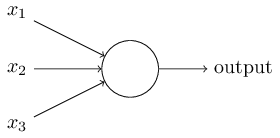
Alors, comment fonctionnent les perceptrons? Le perceptron reçoit plusieurs nombres binaires x ₁ , x ₂ , ... et donne un nombre binaire:



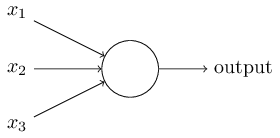
Dans cet exemple, le perceptron a trois numéros d'entrée, x ₁ , x ₂ , x ₃ . En général, il peut y en avoir plus ou moins. Rosenblatt a proposé une règle simple pour calculer le résultat. Il a introduit les poids, w ₁ , w ₂ , nombres réels, exprimant l'importance des nombres d'entrée correspondants pour les résultats. La sortie d'un neurone, 0 ou 1, est déterminée par le fait qu'une somme pondérée est inférieure ou supérieure à un certain seuil [seuil] $$$\ sum_j w_jx_j$ . Comme les poids, le seuil est un nombre réel, un paramètre d'un neurone. En termes mathématiques:

$$

$$output = \ begin {cases} 0 ~ if ~ \ sum_j w_jx_j \ leq seuil \\ 1 ~ if ~ \ sum_j w_jx_j> seuil \ end {cases} \ tag {1}$$

C'est toute la description du perceptron!

Ceci est le modèle mathématique de base. Un perceptron peut être considéré comme un décideur en soupesant les preuves. Permettez-moi de vous donner un exemple pas très réaliste, mais simple. Disons que le week-end approche et que vous avez entendu dire qu'une fête du fromage aura lieu dans votre ville. Vous aimez le fromage et essayez de décider d'aller au festival ou non. Vous pouvez prendre une décision en pesant trois facteurs:

1. Le temps est-il bon?
2. Votre partenaire veut-il vous accompagner?
3. Le festival est-il loin des transports en commun? (Vous n'avez pas de voiture).

Ces trois facteurs peuvent être représentés comme des variables binaires x ₁ , x ₂ , x ₃ . Par exemple, x ₁ = 1 si le temps est bon et 0 s'il fait mauvais. x ₂ = 1 si votre partenaire veut y aller et 0 sinon. Pareil pour x ₃ .

Maintenant, disons que vous êtes tellement fan de fromage que vous êtes prêt à aller au festival, même si votre partenaire ne s'y intéresse pas et qu'il est difficile de s'y rendre. Mais peut-être que vous détestez le mauvais temps, et en cas de mauvais temps, vous n'irez pas au festival. Vous pouvez utiliser des perceptrons pour modéliser un tel processus de prise de décision. Une façon consiste à choisir le poids w ₁ = 6 pour la météo et w ₂ = 2, w ₃ = 2 pour les autres conditions. Une valeur plus grande de w ₁ signifie que la météo compte beaucoup plus pour vous que le fait que votre partenaire vous rejoigne ou la proximité du festival avec un arrêt. Enfin, supposons que vous sélectionnez le seuil 5 pour le perceptron. Avec ces options, le perceptron implémente le modèle de décision souhaité, donnant 1 lorsque le temps est bon et 0 quand il fait mauvais. Le désir du partenaire et la proximité de la butée n'affectent pas la valeur de sortie.

En modifiant les poids et les seuils, nous pouvons obtenir différents modèles de prise de décision. Par exemple, prenons le seuil 3. Ensuite, le perceptron décide que vous devez vous rendre au festival, soit par beau temps, soit lorsque le festival est proche d'un arrêt de bus et que votre partenaire accepte de vous accompagner. En d'autres termes, le modèle est différent. Abaisser le seuil signifie que vous voulez aller plus au festival.

De toute évidence, le perceptron n'est pas un modèle complet de prise de décision humaine! Mais cet exemple montre comment un perceptron peut peser différents types de preuves pour prendre des décisions. Il semble possible qu'un réseau complexe de perceptrons puisse prendre des décisions très complexes:



Dans ce réseau, la première colonne de perceptrons - ce que nous appelons la première couche de perceptrons - prend trois décisions très simples, en pesant les preuves d'entrée. Qu'en est-il des perceptrons de la deuxième couche? Chacun prend une décision, en pesant les résultats de la première couche décisionnelle. De cette façon, le perceptron de la deuxième couche peut prendre une décision à un niveau plus complexe et abstrait par rapport au perceptron de la première couche. Et des décisions encore plus complexes peuvent être prises par des perceptrons sur la troisième couche.De cette façon, un réseau multicouche de perceptrons peut gérer des décisions complexes.

Soit dit en passant, lorsque j'ai déterminé le perceptron, j'ai dit qu'il n'avait qu'une seule valeur de sortie. Mais dans le réseau en haut, les perceptrons semblent avoir plusieurs valeurs de sortie. En fait, ils n'ont qu'une seule issue. De nombreuses flèches de sortie ne sont qu'un moyen pratique de montrer que la sortie du perceptron est utilisée comme entrée de plusieurs autres perceptrons. C'est moins lourd que de dessiner une seule sortie de branchement.

Simplifions la description des perceptrons. Condition$$∑ j w j x j > t r e s h o l d est gênant, et nous pouvons convenir de deux changements à l'enregistrement pour le simplifier. La première consiste à enregistrer$\sum_j w_jx_j > treshold$$$∑ j w j x j comme produit scalaire,$\sum_j w_jx_j$$$w ⋅ x = ∑ j w j x j , où w et x sont des vecteurs dont les composantes sont des poids et des données d'entrée, respectivement. La seconde consiste à transférer le seuil dans une autre partie de l'inégalité, et à le remplacer par une valeur appelée déplacement du perceptron [biais],$w \cdot x = \sum_j w_jx_j$$$$b \equiv −threshold$ . En utilisant le déplacement au lieu d'un seuil, nous pouvons réécrire la règle du perceptron:

$$

$$output = \begin{cases} 0 ~ if ~ w \cdot x + b \leq 0 \\ 1 ~ if ~ w \cdot x + b > 0 \end{cases} \tag{2}$$

Le décalage peut être représenté comme une mesure de la facilité avec laquelle il est possible d'obtenir une valeur de 1 à la sortie du perceptron. Ou, en termes biologiques, le déplacement est une mesure de la facilité d'activation du perceptron. Un perceptron avec un biais très important est extrêmement facile à donner 1. Mais avec un biais négatif très important, cela est difficile à faire. De toute évidence, l'introduction du biais est un petit changement dans la description des perceptrons, mais nous verrons plus tard que cela conduit à une simplification supplémentaire de l'enregistrement. Par conséquent, nous n'utiliserons pas davantage le seuil, mais nous utiliserons toujours le décalage.

J'ai décrit les perceptrons en termes de méthode de pondération des preuves pour la prise de décision. Une autre méthode de leur utilisation est le calcul des fonctions logiques élémentaires, que nous considérons généralement comme les principaux calculs, tels que AND, OR et NAND. Supposons, par exemple, que nous ayons un perceptron avec deux entrées, dont le poids de chacune est -2, et son décalage est 3. Voici: l'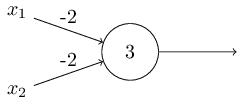



entrée 00 donne la sortie 1, car (−2) ∗ 0 + (- 2 ) ∗ 0 + 3 = 3 est supérieur à zéro. Les mêmes calculs disent que l'entrée 01 et 10 donnent 1. Mais 11 à l'entrée donne 0 à la sortie, puisque (−2) ∗ 1 + (- 2) ∗ 1 + 3 = −1, inférieur à zéro. Par conséquent, notre perceptron implémente la fonction NAND!

Cet exemple montre que les perceptrons peuvent être utilisés pour calculer les fonctions logiques de base. En fait, nous pouvons utiliser les réseaux perceptron pour calculer les fonctions logiques en général. Le fait est que la porte logique NAND est universelle pour les calculs - il est possible de construire n'importe quel calcul sur sa base. Par exemple, vous pouvez utiliser des portes NAND pour créer un circuit qui ajoute deux bits, x ₁ et x ₂ . Pour ce faire, calculez la somme au niveau du bit$$x 1 ⊕ x 2 , ainsi quele drapeau de report, qui est égal à 1 lorsque x₁et x₂sont égal à 1 - c'est-à-dire que le drapeau de report est simplement le résultat d'une multiplication au niveau du bit x₁x₂:pour obtenir le réseau équivalent des perceptrons, nous remplaçons tous Les portes NAND sont des perceptrons avec deux entrées, dont le poids de chacune est -2, et avec un décalage de 3. Voici le réseau résultant. 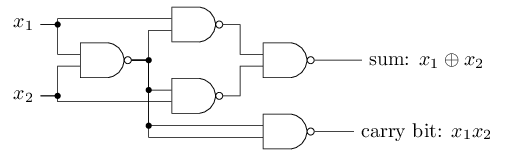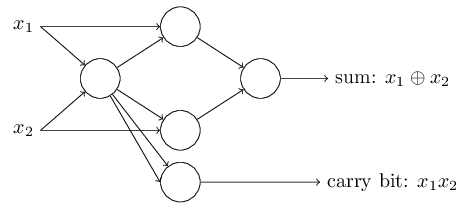Notez que j'ai déplacé le perceptron correspondant à la valve inférieure droite, juste pour le rendre plus pratique pour dessiner des flèches:$x_1 \oplus x_2$







Un aspect remarquable de ce réseau de perceptron est que la sortie de celui le plus à gauche est utilisée deux fois comme entrée vers le bas. Définissant le modèle du perceptron, je n'ai pas évoqué l'admissibilité d'un tel schéma de double sortie au même endroit. En fait, cela n'a pas vraiment d'importance. Si nous ne voulons pas permettre cela, nous pouvons simplement combiner deux lignes avec des poids de -2 en une avec un poids de -4. (Si cela ne vous semble pas évident, arrêtez-vous et prouvez-le). Après ce changement, le réseau se présente comme suit, avec tous les poids non alloués égaux à -2, tous les décalages égaux à 3 et un poids -4 est marqué:



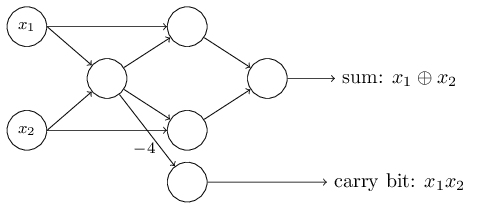Un tel enregistrement de perceptrons qui ont une sortie mais pas d'entrées:



est juste une abréviation. Cela ne signifie pas qu'il n'a pas d'entrées. Pour comprendre cela, supposons que nous ayons un perceptron sans entrées. Alors la somme pondérée ∑ _j w _j x _j serait toujours nulle, donc le perceptron donnerait 1 pour b> 0 et 0 pour b ≤ 0. Autrement dit, le perceptron donnerait juste une valeur fixe, et non ce dont nous avons besoin (x ₁ dans l'exemple ci-dessus). Il vaut mieux considérer les perceptrons d'entrée non pas comme des perceptrons, mais comme des unités spéciales qui sont simplement définies de manière à produire les valeurs souhaitées x ₁ , x ₂ , ...

L'exemple d'additionneur montre comment un réseau perceptron peut être utilisé pour simuler un circuit contenant de nombreuses portes NAND. Et comme ces portes sont universelles pour les calculs, les perceptrons sont donc universels pour les calculs.

La polyvalence informatique des perceptrons est à la fois encourageante et décevante. C'est encourageant, car le réseau perceptron peut être aussi puissant que n'importe quel autre appareil informatique. Décevant, donnant l'impression que les perceptrons ne sont qu'un nouveau type de porte logique NAND. Découverte so-so!

Cependant, la situation est en fait meilleure. Il s'avère que nous pouvons développer des algorithmes de formation qui peuvent ajuster automatiquement les poids et les déplacements du réseau à partir des neurones artificiels. Cet ajustement a lieu en réponse à des stimuli externes, sans l'intervention directe d'un programmeur. Ces algorithmes d'apprentissage nous permettent d'utiliser les neurones artificiels d'une manière radicalement différente des portes logiques ordinaires. Au lieu d'enregistrer explicitement un circuit à partir de portes NAND et autres, nos réseaux de neurones peuvent simplement apprendre à résoudre des problèmes, parfois ceux pour lesquels il serait extrêmement difficile de concevoir directement un circuit régulier.

Neurones sigmoïdes

Les algorithmes d'apprentissage sont excellents. Cependant, comment développer un tel algorithme pour un réseau neuronal? Supposons que nous ayons un réseau de perceptrons que nous voulons utiliser pour nous former à la résolution d'un problème. Supposons que l'entrée sur le réseau puisse être des pixels d'une image numérisée d'un chiffre manuscrit. Et nous voulons que le réseau connaisse les poids et décalages nécessaires pour classer correctement les nombres. Pour comprendre comment une telle formation peut fonctionner, imaginons que nous modifions légèrement un certain poids (ou biais) dans le réseau. Nous voulons que ce petit changement entraîne un petit changement dans la sortie du réseau. Comme nous le verrons bientôt, cette propriété rend l'apprentissage possible. Schématiquement, nous voulons ce qui suit (évidemment, un tel réseau est trop simple pour reconnaître l'écriture manuscrite!):



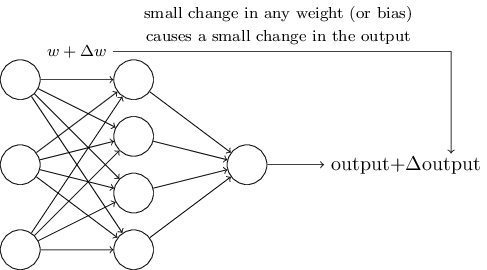
Si un petit changement de poids (ou biais) entraînait un petit changement dans le résultat de sortie, nous pourrions changer les poids et les biais afin que notre réseau se comporte un peu plus près de ce que nous voulons. Par exemple, disons que le réseau a incorrectement attribué l'image à «8», alors qu'elle aurait dû l'être à «9». Nous pourrions trouver comment faire un petit changement de poids et de déplacement afin que le réseau se rapproche un peu plus de la classification de l'image en «9». Et puis nous répétions cela, en changeant de poids et en changeant encore et encore pour obtenir le meilleur et le meilleur résultat. Le réseau apprendrait.

Le problème est que s'il y a des perceptrons dans le réseau, cela ne se produit pas. Un petit changement dans les poids ou le déplacement d'un perceptron peut parfois conduire à un changement de sa sortie à l'opposé, par exemple de 0 à 1. Un tel retournement peut changer le comportement du reste du réseau d'une manière très compliquée. Et même si maintenant notre «9» est correctement reconnu, le comportement du réseau avec toutes les autres images a probablement complètement changé d'une manière difficile à contrôler. Pour cette raison, il est difficile d'imaginer comment nous pouvons progressivement ajuster les poids et les décalages afin que le réseau se rapproche progressivement du comportement souhaité. Il existe peut-être un moyen intelligent de contourner ce problème. Mais il n'y a pas de solution simple au problème de l'apprentissage d'un réseau de perceptrons.

Ce problème peut être contourné en introduisant un nouveau type de neurone artificiel appelé neurone sigmoïde. Ils sont similaires aux perceptrons, mais modifiés de sorte que de petits changements dans les poids et les décalages n'entraînent que de petits changements dans la sortie. C'est un fait fondamental qui permettra au réseau de neurones sigmoïdes d'apprendre.

Permettez-moi de décrire un neurone sigmoïde. Nous les dessinerons de la même manière que les perceptrons:



Il a la même entrée x ₁ , x ₂ , ... Mais au lieu d'être égal à 0 ou 1, ces entrées peuvent avoir n'importe quelle valeur dans la plage de 0 à 1. Par exemple, une valeur de 0,638 sera une entrée valide pour neurone sigmoïde (CH). Tout comme le perceptron, SN a des poids pour chaque entrée, w ₁ , w ₂ , ... et le biais total b. Mais sa valeur de sortie ne sera pas 0 ou 1. Ce sera σ (w⋅x + b), où σ est le sigmoïde.

Soit dit en passant, σ est parfois appelé une fonction logistique , et cette classe de neurones est appelée neurones logistiques. Il est utile de se souvenir de cette terminologie, car ces termes sont utilisés par de nombreuses personnes travaillant avec des réseaux de neurones. Cependant, nous respecterons la terminologie sigmoïde.

La fonction est définie comme suit:

$$

$$\ sigma (z) \ equiv \ frac {1} {1 + e ^ {- z}} \ tag {3}$$

Dans notre cas, la valeur de sortie du neurone sigmoïde avec les données d'entrée x ₁ , x ₂ , ... par les poids w ₁ , w ₂ , ... et le décalage b sera considérée comme:

$$

$$\ frac {1} {1 + exp (- \ sum_j w_jx_j - b)} \ tag {4}$$

À première vue, le CH semble complètement différent des neurones. L'aspect algébrique d'un sigmoïde peut sembler déroutant et obscur si vous ne le connaissez pas. En fait, il existe de nombreuses similitudes entre les perceptrons et SN, et la forme algébrique d'un sigmoïde s'avère être plus un détail technique qu'un sérieux obstacle à la compréhension.

Pour comprendre les similitudes avec le modèle du perceptron, supposons que z ≡ w ⋅ x + b est un grand nombre positif. Alors e - z ≈ 0, donc, σ (z) ≈ 1. En d'autres termes, lorsque z = w ⋅ x + b est grand et positif, le rendement SN est d'environ 1, comme dans le perceptron. Supposons que z = w ⋅ x + b est grand avec un signe moins. Alors e - z → ∞, et σ (z) ≈ 0. Ainsi, pour un grand z avec un signe moins, le comportement du SN se rapproche également du perceptron. Et ce n'est que lorsque w ⋅ x + b a une taille moyenne que l'on observe de graves écarts par rapport au modèle du perceptron.

Qu'en est-il de la forme algébrique de σ? Comment le comprenons-nous? En fait, la forme exacte de σ n'est pas si importante - la forme de la fonction sur le graphique est importante. Le voici:



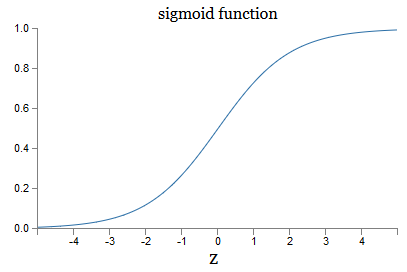
Il s'agit d'une version fluide de la fonction pas à pas:



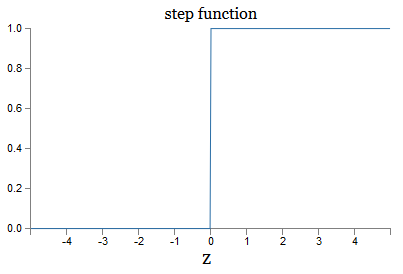
Si σ était pas à pas, alors le SN serait un perceptron, car il aurait une sortie 0 ou 1 selon le signe w ⋅ x + b (enfin, en fait, à z = 0, le perceptron donne 0 et la fonction de pas 1 , donc à ce stade, la fonction devrait être modifiée).

En utilisant la fonction réelle σ, nous obtenons un perceptron lissé. Et l'essentiel ici est la fluidité de la fonction, pas sa forme exacte. La régularité signifie que de petits changements, les poids Δw _j et les décalages δb donneront de petits changements Δsortie de la sortie. L'algèbre nous dit que la sortie Δ est bien approximée comme suit:

$$

$$\ Sortie Delta \ approx \ sum_j \ frac {\ sortie partielle} {\ partial w_j} \ Delta w_j + \ frac {\ sortie partielle} {\ partial b} \ Delta b \ tag {5}$$

Lorsque la somme est sur tous les poids w _j , et ∂sortie / ∂w _j et ∂sortie / ∂b désignent les dérivées partielles de la sortie par rapport à w _j et b, respectivement. Ne paniquez pas si vous ne vous sentez pas en sécurité en compagnie de dérivés privés! Bien que la formule semble compliquée, avec toutes ces dérivées partielles, elle dit en fait quelque chose de assez simple (et utile): la sortie Δ est une fonction linéaire en fonction des poids et des biais Δw _j et Δb. Sa linéarité facilite la sélection de petits changements de poids et de décalages pour obtenir le biais de sortie souhaité. Ainsi, bien que les SN soient similaires aux perceptrons dans leur comportement qualitatif, ils permettent de comprendre plus facilement comment la sortie peut être modifiée en changeant les poids et les déplacements.

Si la forme générale σ est importante pour nous, et non sa forme exacte, alors pourquoi utilisons-nous une telle formule (3)? En fait, plus tard, nous considérerons parfois les neurones dont la sortie est f (w ⋅ x + b), où f () est une autre fonction d'activation. La principale chose qui change lorsque la fonction change est la valeur des dérivées partielles dans l'équation (5). Il s'avère que lorsque nous calculons ensuite ces dérivées partielles, l'utilisation de σ simplifie considérablement l'algèbre, car les exposants ont de très belles propriétés lors de la différenciation. Dans tous les cas, σ est souvent utilisé pour travailler avec des réseaux de neurones, et le plus souvent dans ce livre, nous utiliserons une telle fonction d'activation.

Comment interpréter le résultat du travail de CH? Évidemment, la principale différence entre les perceptrons et le CH est que le CH ne donne pas seulement 0 ou 1. Leur sortie peut être n'importe quel nombre réel de 0 à 1, donc des valeurs comme 0,173 ou 0,689 sont valides. Cela peut être utile, par exemple, si vous souhaitez que la valeur de sortie indique, par exemple, la luminosité moyenne des pixels de l'image reçue à l'entrée du NS. Mais parfois, cela peut être gênant. Supposons que nous voulions que la sortie réseau dise que «l'image 9 a été entrée» ou «l'image d'entrée n'est pas 9». Évidemment, ce serait plus facile si les valeurs de sortie étaient 0 ou 1, comme un perceptron. Mais en pratique, nous pouvons convenir que toute valeur de sortie d'au moins 0,5 signifierait «9» à l'entrée, et toute valeur inférieure à 0,5 signifierait qu'elle n'est «pas 9». J'indiquerai toujours explicitement l'existence de tels accords.

Exercices

• CH simulant les perceptrons, partie 1

Supposons que nous prenions tous les poids et décalages d'un réseau de perceptrons et les multiplions par une constante positive c> 0. Montrez que le comportement du réseau ne change pas.

• CH simulant les perceptrons, partie 2

Supposons que nous ayons la même situation que dans le problème précédent - un réseau de perceptrons. Supposons également que les données d'entrée du réseau soient sélectionnées. Nous n'avons pas besoin d'une valeur spécifique, l'essentiel est qu'elle soit fixe. Supposons que les poids et les déplacements soient tels que w⋅x + b ≠ 0, où x est la valeur d'entrée de tout perceptron du réseau. Maintenant, nous remplaçons tous les perceptrons du réseau par SN, et multiplions les poids et les déplacements par la constante positive c> 0. Montrer qu'à la limite c → ∞ le comportement du réseau du SN sera exactement le même que celui des réseaux de perceptrons. Comment cette affirmation sera-t-elle violée si pour l'un des perceptrons w⋅x + b = 0?

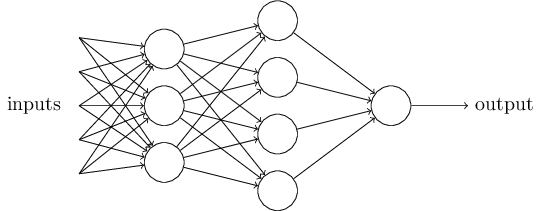
Architecture de réseau neuronal

Dans la section suivante, je présenterai un réseau neuronal capable d'une bonne classification des nombres manuscrits. Avant cela, il est utile d'expliquer la terminologie qui nous permet de pointer vers différentes parties du réseau. Disons que nous avons le réseau suivant:



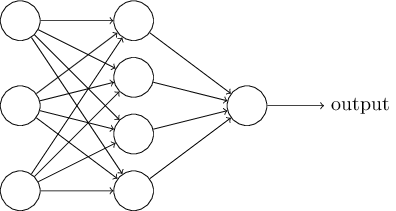
Comme je l'ai mentionné, la couche la plus à gauche du réseau s'appelle la couche d'entrée et ses neurones sont appelés neurones d'entrée. La couche la plus à droite, ou couche de sortie, contient des neurones de sortie, ou, comme dans notre cas, un neurone de sortie. La couche intermédiaire est appelée cachée, car ses neurones ne sont ni entrée ni sortie. Le terme «caché» peut sembler un peu mystérieux - lorsque je l'ai entendu pour la première fois, j'ai décidé qu'il devait avoir une profonde importance philosophique ou mathématique - mais il ne signifie que «ni entrée ni sortie». Le réseau ci-dessus n'a qu'une seule couche cachée, mais certains réseaux ont plusieurs couches cachées. Par exemple, dans le réseau à quatre couches suivant, il existe deux couches masquées:



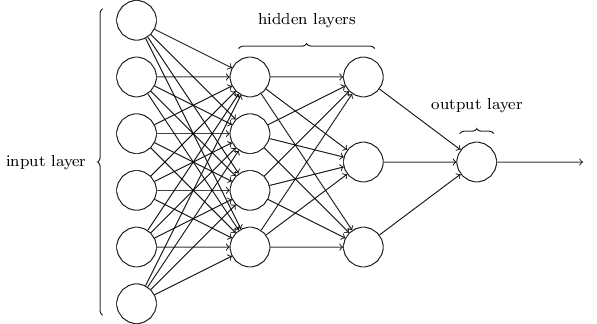
Cela peut être déroutant, mais pour des raisons historiques, ces réseaux multicouches sont parfois appelés perceptrons multicouches, MLP, en dépit du fait qu'ils sont constitués de neurones sigmoïdes plutôt que de perceptrons. Je ne vais pas utiliser une telle terminologie car elle prête à confusion, mais je dois mettre en garde contre son existence.

La conception de couches d'entrée et de sortie est parfois une tâche simple. Par exemple, supposons que nous essayons de déterminer si le nombre manuscrit signifie «9» ou non. Un circuit de réseau naturel codera la luminosité des pixels de l'image dans les neurones d'entrée. Si l'image est en noir et blanc, d'une taille de 64 x 64 pixels, nous aurons alors 64 x 64 = 4096 neurones d'entrée, avec une luminosité dans la plage de 0 à 1. La couche de sortie ne contiendra qu'un seul neurone, dont la valeur inférieure à 0,5 signifiera que "on l'entrée n'était pas 9 ", mais des valeurs plus signifieront que" l'entrée était 9 ".

Et bien que la conception de couches d'entrée et de sortie soit souvent une tâche simple, la conception de couches cachées peut être un art difficile. En particulier, il n'est pas possible de décrire le processus de développement de couches cachées avec quelques règles de base simples. Les chercheurs de l'Assemblée nationale ont développé de nombreuses règles heuristiques pour la conception de couches cachées qui aident à obtenir le comportement souhaité des réseaux de neurones. Par exemple, une telle heuristique peut être utilisée pour comprendre comment parvenir à un compromis entre le nombre de couches cachées et le temps disponible pour la formation du réseau. Plus tard, nous rencontrerons certaines de ces règles.

Jusqu'à présent, nous avons discuté des NS dans lesquels la sortie d'une couche est utilisée comme entrée pour la suivante. Ces réseaux sont appelés réseaux de neurones à distribution directe. Cela signifie qu'il n'y a pas de boucles dans le réseau - les informations vont toujours de l'avant et ne reviennent jamais. Si nous avions des boucles, nous rencontrerions des situations dans lesquelles le sigmoïde d'entrée dépendrait de la sortie. Ce serait difficile à comprendre et nous n'autorisons pas de telles boucles.

Cependant, il existe d'autres modèles de NS artificiels dans lesquels il est possible d'utiliser des boucles de rétroaction. Ces modèles sont appelés réseaux de neurones récurrents (RNS). L'idée de ces réseaux est que leurs neurones sont activés pour des périodes de temps limitées. Cette activation peut stimuler d'autres neutrons, qui peuvent être activés un peu plus tard, également pour une durée limitée. Cela conduit à l'activation des neurones suivants, et au fil du temps, nous obtenons une cascade de neurones activés. Les boucles dans de tels modèles ne présentent pas de problèmes, car la sortie d'un neurone affecte son entrée ultérieurement, et pas immédiatement.

Les RNS n'étaient pas aussi influents que les NS de distribution directe, en particulier parce que les algorithmes de formation pour les RNS ont jusqu'à présent moins de potentiel. Cependant, le RNS reste toujours extrêmement intéressant. Dans l'esprit du travail, ils sont beaucoup plus proches du cerveau que les NS de distribution directe. Il est possible que le RNS soit en mesure de résoudre des problèmes importants qui peuvent être résolus avec de grandes difficultés à l'aide de la distribution directe NS. Cependant, afin de limiter la portée de notre étude, nous nous concentrerons sur les NS de distribution directe les plus largement utilisés.

Réseau de classification d'encre simple

Après avoir défini les réseaux de neurones, nous reviendrons à la reconnaissance de l'écriture manuscrite. La tâche de reconnaissance des nombres manuscrits peut être divisée en deux sous-tâches. Premièrement, nous voulons trouver un moyen de diviser une image contenant plusieurs chiffres en une séquence d'images individuelles, chacune contenant un chiffre. Par exemple, nous aimerions diviser l'image



en six séparés



Nous, les humains, pouvons facilement résoudre ce problème de segmentation, mais il est difficile pour un programme informatique de diviser correctement l'image. Après la segmentation, le programme doit classer chaque chiffre individuel. Ainsi, par exemple, nous voulons que notre programme reconnaisse que le premier chiffre



c'est 5.

Nous nous concentrerons sur la création d'un programme pour résoudre le deuxième problème, la classification des nombres individuels. Il s'avère que le problème de la segmentation n'est pas si difficile à résoudre dès que nous trouvons un bon moyen de classer les chiffres individuels. Il existe de nombreuses approches pour résoudre le problème de segmentation. L'un d'eux consiste à essayer de nombreuses manières différentes de segmenter l'image en utilisant le classificateur de chiffres individuels, en évaluant chaque tentative. La segmentation d'essai est très appréciée si le classificateur de chiffres individuels est confiant dans la classification de tous les segments, et faible si elle a des problèmes dans un ou plusieurs segments. L'idée est que si le classificateur a des problèmes quelque part, cela signifie très probablement que la segmentation est incorrecte. Cette idée et d'autres options peuvent être utilisées pour une bonne solution au problème de segmentation. Ainsi, au lieu de nous soucier de la segmentation, nous nous concentrerons sur le développement d'une NS capable de résoudre une tâche plus intéressante et complexe, à savoir la reconnaissance de nombres manuscrits individuels.

Pour reconnaître des chiffres individuels, nous utiliserons NS à partir de trois couches:



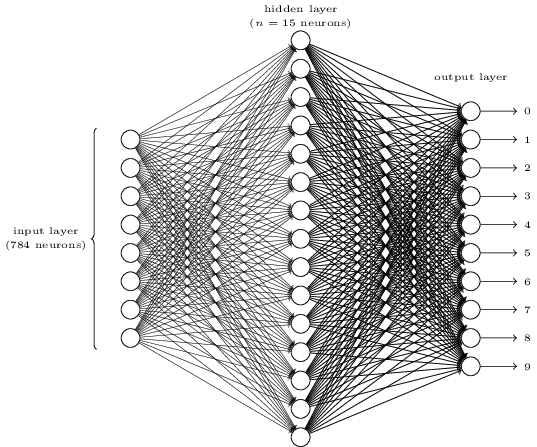
La couche réseau d'entrée contient des neurones codant diverses valeurs des pixels d'entrée. Comme cela sera indiqué dans la section suivante, nos données d'entraînement seront constituées de nombreuses images de chiffres manuscrits numérisés de 28x28 pixels, de sorte que la couche d'entrée contient 28x28 = 784 neurones. Par souci de simplicité, je n'ai pas indiqué la plupart des 784 neurones du diagramme. Les pixels entrants sont en noir et blanc, avec une valeur de 0,0 indiquant le blanc, 1,0 indiquant le noir et des valeurs intermédiaires indiquant des nuances de gris de plus en plus sombres.

La deuxième couche du réseau est masquée. Nous dénotons le nombre de neurones dans cette couche n, et nous expérimenterons différentes valeurs de n. L'exemple ci-dessus montre une petite couche cachée ne contenant que n = 15 neurones.

Il y a 10 neurones dans la couche de sortie du réseau. Si le premier neurone est activé, c'est-à-dire que sa valeur de sortie est ≈ 1, cela indique que le réseau considère que l'entrée était 0. Si le deuxième neurone est activé, le réseau pense que l'entrée était 1. Et ainsi de suite. À strictement parler, nous numérotons les neurones de sortie de 0 à 9 et regardons lesquels d'entre eux avaient la valeur d'activation maximale. S'il s'agit, par exemple, du neurone n ° 6, alors notre réseau pense que l'entrée était le numéro 6. Et ainsi de suite.

Vous vous demandez peut-être pourquoi nous devons utiliser dix neurones. Après tout, nous voulons savoir quel chiffre de 0 à 9 correspond à l'image d'entrée. Il serait naturel de n'utiliser que 4 neurones de sortie, dont chacun prendrait une valeur binaire, selon que sa valeur de sortie est plus proche de 0 ou 1. Quatre neurones suffiraient, puisque 2 ⁴ = 16, plus de 10 valeurs possibles. Pourquoi notre réseau devrait-il utiliser 10 neurones? Est-ce inefficace? La base de ceci est empirique; nous pouvons essayer les deux variantes du réseau, et il s'avère que pour cette tâche, un réseau avec 10 neurones de sortie est mieux formé pour reconnaître les nombres qu'un réseau avec 4. Cependant, la question demeure: pourquoi 10 neurones de sortie sont-ils meilleurs? Y a-t-il une heuristique qui nous indiquerait à l'avance que 10 neurones de sortie devraient être utilisés au lieu de 4?

Pour comprendre pourquoi, il est utile de réfléchir à ce que fait un réseau de neurones. Considérons d'abord l'option avec 10 neurones de sortie. Nous nous concentrons sur le premier neurone de sortie, qui essaie de décider si l'image entrante est nulle. Il le fait en pesant les preuves obtenues à partir d'une couche cachée. Que font les neurones cachés? Supposons que le premier neurone de la couche cachée détermine s'il y a quelque chose comme ça dans l'image:



Il peut le faire en attribuant de gros poids aux pixels correspondant à cette image et de petits poids aux autres. De la même manière, supposons que les deuxième, troisième et quatrième neurones de la couche cachée recherchent la présence de fragments similaires dans l'image:



Comme vous l'avez peut-être deviné, ces quatre fragments donnent ensemble l'image 0 que nous avons vue plus tôt:



Donc, si les quatre neurones cachés sont activés, nous pouvons conclure que le nombre est 0. Bien sûr, ce n'est pas la seule preuve que 0 y était affiché - nous pouvons obtenir 0 de bien d'autres façons (en décalant légèrement ces images ou en les déformant légèrement). Cependant, nous pouvons dire avec certitude que, au moins dans ce cas, nous pouvons conclure qu'il y avait 0 à l'entrée.

Si nous supposons que le réseau fonctionne ainsi, nous pouvons expliquer de manière plausible pourquoi il vaut mieux utiliser 10 neurones de sortie au lieu de 4. Si nous avions 4 neurones de sortie, le premier neurone essaierait de décider quel est le bit le plus significatif du chiffre entrant. Et il n'y a pas de moyen facile d'associer le bit le plus significatif aux formes simples données ci-dessus. Il est difficile d'imaginer des raisons historiques pour lesquelles des parties de la forme d'un chiffre seraient en quelque sorte liées au bit le plus significatif de la sortie.

Cependant, tout ce qui précède n'est pris en charge que par l'heuristique. Rien ne parle en faveur du fait qu'un réseau à trois couches devrait fonctionner comme je l'ai dit, et les neurones cachés devraient trouver de simples composants de formes. Peut-être que l'algorithme d'apprentissage délicat trouvera des poids qui nous permettront d'utiliser seulement 4 neurones de sortie. Cependant, en tant qu'heuristique, ma méthode fonctionne bien et peut vous faire gagner un temps considérable dans le développement d'une bonne architecture NS.

Exercices

• , . , . . , 3 , ( ) 0,99, 0,01.

Donc, nous avons le schéma NA - comment apprendre à reconnaître les nombres? La première chose dont nous avons besoin, ce sont les données d'entraînement, ensemble de données de formation. Nous utiliserons le kit MNIST contenant des dizaines de milliers d'images numérisées de nombres manuscrits et leur classification correcte. Le nom MNIST a été reçu car il s'agit d'un sous-ensemble modifié des deux ensembles de données collectés par le NIST , l'Institut national américain des normes et de la technologie. Voici quelques images de MNIST:



Ce sont les mêmes nombres qui ont été donnés au début du chapitre comme tâche de reconnaissance. Bien sûr, lors de la vérification de la NS, nous lui demanderons de reconnaître les mauvaises images qui étaient déjà dans le kit d'entraînement!

Les données du MNIST se composent de deux parties. La première contient 60 000 images destinées à la formation. Il s'agit de manuscrits numérisés de 250 personnes, dont la moitié étaient des employés du US Census Bureau et l'autre moitié, des lycéens. Les images sont en noir et blanc, mesurant 28x28 pixels. La deuxième partie de l'ensemble de données MNIST comprend 10 000 images pour tester le réseau. Il s'agit également d'une image en noir et blanc de 28x28 pixels. Nous utiliserons ces données pour évaluer dans quelle mesure le réseau a appris à reconnaître les nombres. Pour améliorer la qualité de l'évaluation, ces chiffres ont été tirés de 250 autres personnes qui n'ont pas participé à l'enregistrement de l'ensemble de formation (bien qu'il s'agisse également d'employés du Bureau et d'élèves du secondaire). Cela nous aide à nous assurer que notre système peut reconnaître l'écriture manuscrite des personnes qu'il n'a pas rencontrées lors de la formation.

L'entrée d'apprentissage sera indiquée par x. Il sera commode de traiter chaque image d'entrée x comme un vecteur avec 28x28 = 784 mesures. Chaque valeur à l'intérieur du vecteur indique la luminosité d'un pixel dans l'image. Nous désignerons la valeur de sortie par y = y (x), où y est un vecteur à dix dimensions. Par exemple, si une certaine image d'apprentissage x contient 6, alors y (x) = (0,0,0,0,0,0,1,1,0,0,0) ^T sera le vecteur dont nous avons besoin. T est une opération de transposition qui transforme un vecteur ligne en vecteur colonne.

Nous voulons trouver un algorithme qui nous permet de rechercher de tels poids et décalages de sorte que la sortie du réseau approche y (x) pour toutes les entrées d'apprentissage x. Pour quantifier l'approximation de cet objectif, nous définissons une fonction de coût (parfois appelée fonction de perte; dans le livre, nous utiliserons la fonction de coût, mais gardez à l'esprit un autre nom):

$$

$$C(w, b) = \frac{1}{2n} \sum_x || y(x) – a ||^2 \tag{6}$$

Ici w désigne un ensemble de poids de réseau, b est un ensemble de décalages, n est le nombre de données d'entrée d'apprentissage, a est le vecteur de données de sortie lorsque x est des données d'entrée, et la somme passe par toutes les entrées d'apprentissage x. La sortie, bien sûr, dépend de x, w et b, mais pour simplifier je n'ai pas désigné cette dépendance. La notation || v || signifie la longueur du vecteur v. Nous appellerons C une fonction de coût quadratique; parfois, il est également appelé l'erreur standard, ou MSE. Si vous regardez attentivement C, vous pouvez voir qu'il n'est pas négatif, car tous les membres de la somme ne sont pas négatifs. De plus, le coût de C (w, b) devient petit, c'est-à-dire C (w, b) ≈ 0, précisément lorsque y (x) est approximativement égal au vecteur de sortie a pour toutes les données d'entrée d'apprentissage x. Donc, notre algorithme a bien fonctionné si nous avons réussi à trouver des poids et des décalages tels que C (w, b) ≈ 0. Et vice versa, il a mal fonctionné lorsque C (w,b) grand - cela signifie que y (x) ne correspond pas à la sortie pour une grande quantité d'entrée. Il s'avère que l'objectif de l'algorithme d'apprentissage est de minimiser le coût de C (w, b) en fonction des poids et des décalages. En d'autres termes, nous devons trouver un ensemble de poids et de compensations qui minimisent la valeur du coût. Nous le ferons en utilisant un algorithme appelé descente de gradient.

Pourquoi avons-nous besoin d'une valeur quadratique? Ne sommes-nous pas principalement intéressés par le nombre d'images correctement reconnues par le réseau? Est-il possible de simplement maximiser ce nombre directement et de ne pas minimiser la valeur intermédiaire de la valeur quadratique? Le problème est que le nombre d'images correctement reconnues n'est pas une fonction régulière des poids et décalages du réseau. Dans la plupart des cas, de petits changements de poids et de décalages ne changeront pas le nombre d'images correctement reconnues. Pour cette raison, il est difficile de comprendre comment changer les poids et les biais pour améliorer l'efficacité. Si nous utilisons une fonction de coût lisse, il nous sera facile de comprendre comment faire de petits changements dans les poids et les compensations afin d'améliorer le coût. Par conséquent, nous nous concentrerons d'abord sur la valeur quadratique, puis nous étudierons la précision de la classification.

Même si nous voulons utiliser une fonction de coût lisse, vous vous demandez peut-être pourquoi nous avons choisi la fonction quadratique pour l'équation (6)? N'est-il pas possible de le choisir arbitrairement? Peut-être que si nous choisissions une fonction différente, nous obtiendrions un ensemble complètement différent de minimisation des poids et des décalages? Une question raisonnable, et plus tard nous examinerons à nouveau la fonction de coût et y apporterons quelques corrections. Cependant, la fonction de coût quadratique fonctionne très bien pour comprendre les choses de base dans l'apprentissage de la NS, donc pour l'instant nous nous y tiendrons.

Pour résumer: notre objectif dans la formation NS est de trouver des poids et des compensations qui minimisent la fonction de coût quadratique C (w, b). La tâche est bien posée, mais jusqu'à présent, elle a de nombreuses structures distrayantes - l'interprétation de w et b en tant que poids et décalages, la fonction σ cachée en arrière-plan, le choix de l'architecture du réseau, MNIST, etc. Il s'avère que nous pouvons comprendre beaucoup de choses, en ignorant la plupart de cette structure et en nous concentrant uniquement sur l'aspect de la minimisation. Donc, pour l'instant, nous oublierons la forme particulière de la fonction de coût, la communication avec l'Assemblée nationale, etc. Au lieu de cela, nous allons imaginer que nous avons juste une fonction avec de nombreuses variables, et nous voulons la minimiser. Nous allons développer une technologie appelée descente de gradient, qui peut être utilisée pour résoudre de tels problèmes. Et puis nous revenons à une certaine fonction,que nous voulons minimiser pour l'Assemblée nationale.

Eh bien, disons que nous essayons de minimiser une fonction C (v). Cela peut être n'importe quelle fonction avec des valeurs réelles de nombreuses variables v = v ₁ , v ₂ , ... Notez que j'ai remplacé la notation w et b par v pour montrer que cela peut être n'importe quelle fonction - nous ne sommes plus obsédés par HC. Il est utile d'imaginer qu'une fonction C n'a que deux variables - v ₁ et v ₂ :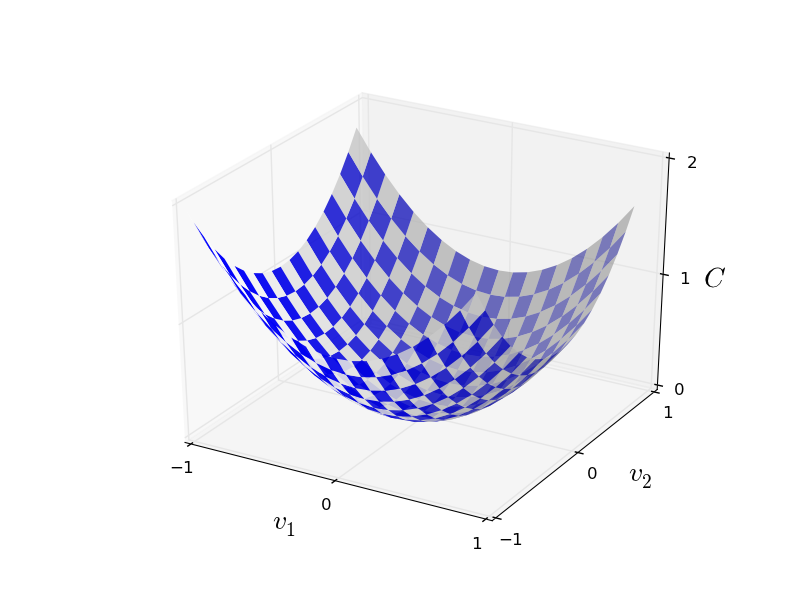



Nous aimerions trouver où C atteint un minimum global. Bien sûr, avec la fonction dessinée ci-dessus, nous pouvons étudier le graphique et trouver le minimum. En ce sens, je vous ai peut-être donné une fonction trop simple! Dans le cas général, C peut être une fonction complexe de nombreuses variables, et il est généralement impossible de simplement regarder le graphique et de trouver le minimum.

Une façon de résoudre le problème consiste à utiliser l'algèbre pour trouver le minimum analytiquement. Nous pouvons calculer les dérivées et essayer de les utiliser pour trouver l'extremum. Si nous avons de la chance, cela fonctionnera lorsque C est fonction d'une ou deux variables. Mais avec beaucoup de variables, cela se transforme en cauchemar. Et pour les NS, nous avons souvent besoin de beaucoup plus de variables - pour les plus grandes NS, les fonctions de coût dépendent de manière complexe de milliards de poids et de déplacements. L'utilisation de l'algèbre pour minimiser ces fonctions échouera!

(Ayant déclaré qu'il serait plus commode pour nous de considérer C comme une fonction de deux variables, j'ai dit deux fois dans deux paragraphes «oui, mais que se passe-t-il s'il s'agit d'une fonction d'un nombre beaucoup plus grand de variables?» Je m'excuse. Croyez-nous, il nous sera vraiment utile de représenter C comme une fonction deux variables, c'est juste que parfois cette image se désagrège, c'est pourquoi les deux paragraphes précédents étaient nécessaires, pour le raisonnement mathématique il est souvent nécessaire de jongler avec plusieurs représentations intuitives, en apprenant en même temps quand la représentation peut être utilisée et quand non ZYA.)

D'accord, cela signifie que l'algèbre ne fonctionnera pas. Heureusement, il existe une grande analogie qui offre un algorithme qui fonctionne bien. Nous imaginons notre fonction comme quelque chose comme une vallée. Avec le dernier calendrier, ce ne sera pas si difficile à faire. Et nous imaginons une balle roulant le long de la pente de la vallée. Notre expérience nous dit que la balle finira par glisser jusqu'au fond. Peut-être pouvons-nous utiliser cette idée pour trouver le minimum d'une fonction? Nous sélectionnons au hasard le point de départ d'une balle imaginaire, puis simulons le mouvement de la balle, comme si elle roulait au fond de la vallée. Nous pouvons utiliser cette simulation simplement en comptant les dérivées (et, éventuellement, les dérivées secondes) de C - elles nous diront tout sur la forme locale de la vallée, et donc sur la façon dont notre balle roulera.

Sur la base de ce que vous avez écrit, vous pourriez penser que nous noterons les équations de mouvement de Newton pour la balle, examinerons les effets de la friction et de la gravité, etc. En fait, nous ne serons pas si près de suivre cette analogie avec la balle - nous développons un algorithme pour minimiser C, et non une simulation exacte des lois de la physique! Cette analogie devrait stimuler notre imagination et ne pas limiter notre réflexion. Donc, au lieu de plonger dans les détails complexes de la physique, posons la question: si nous étions nommés dieu pour une journée, et nous créerions nos propres lois de la physique, en disant à la balle comment faire rouler quelle loi ou les lois du mouvement que nous choisirions, afin que la balle roule toujours sur au fond de la vallée?

Pour clarifier le problème, nous réfléchirons à ce qui se passe si nous déplaçons la balle sur une petite distance Δv ₁ dans la direction de v ₁, et une petite distance Δv ₂ en direction de v ₂ . L'algèbre nous dit que C change comme suit:

$$

$$\Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2 \tag{7}$$

Nous trouverons un moyen de choisir ces Δv ₁ et Δv ₂ pour que ΔC soit inférieur à zéro; c'est-à-dire que nous les sélectionnerons pour que la balle roule. Pour comprendre comment procéder, il est utile de définir Δv comme vecteur de changements, c'est-à-dire Δv ≡ (Δv ₁ , Δv ₂ ) ^T , où T est l'opération de transposition qui transforme les vecteurs ligne en vecteurs colonne. On définit également le vecteur de gradient en tant que C dérivées partielles (∂S / ∂v ₁ , ∂S / ∂v ₂ ) ^T . On note le vecteur de gradient par ∇:

$$

$$\nabla C \equiv (\frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2})^T \tag{8}$$

Bientôt, nous réécrirons le changement de ΔC à Δv et du gradient ∇C. En attendant, je veux clarifier quelque chose, à cause de quoi les gens s'accrochent souvent au dégradé. Lors de leur première rencontre avec ∇C, les gens ne comprennent parfois pas comment ils devraient percevoir le symbole ∇. Qu'est-ce que cela signifie spécifiquement? En fait, vous pouvez considérer en toute sécurité ∇C un seul objet mathématique - un vecteur défini précédemment - qui est simplement écrit en utilisant deux caractères. De ce point de vue, ∇ est comme agiter un drapeau informant que "∇C est un vecteur de gradient". Il existe des points de vue plus avancés à partir desquels ∇ peut être considéré comme une entité mathématique indépendante (par exemple, comme un opérateur de différenciation), mais nous n'en avons pas besoin.

Avec de telles définitions, l'expression (7) peut être réécrite comme:

$$

$$\Delta C \approx \nabla C \cdot \Delta v \tag{9}$$

Cette équation permet d'expliquer pourquoi ∇C est appelé un vecteur de gradient: il relie les changements de v aux changements de C, comme prévu par une entité appelée gradient. [eng. gradient - écart / env. transl.] Cependant, il est plus intéressant que cette équation nous permette de voir comment choisir Δv pour que ΔC soit négatif. Disons que nous choisissons

$$

$$\Delta v = - \eta \nabla C \tag{10}$$

où η est un petit paramètre positif (vitesse d'apprentissage). Alors l'équation (9) nous dit que ΔC ≈ - η ∇C ⋅ ∇C = - η || ∇C || ² . Depuis || ∇C || ² ≥ 0, cela garantit que ΔC ≤ 0, c'est-à-dire que C diminuera tout le temps si nous changeons v, comme prescrit en (10) (bien sûr, dans le cadre de l'approximation de l'équation (9)). Et c'est exactement ce dont nous avons besoin! Par conséquent, nous prenons l'équation (10) pour déterminer la "loi de mouvement" de la balle dans notre algorithme de descente de gradient. Autrement dit, nous utiliserons l'équation (10) pour calculer la valeur Δv, puis nous déplacerons la balle à cette valeur:

$$

$$v \rightarrow v' = v - \eta \nabla C \tag{11}$$

Ensuite, nous appliquons à nouveau cette règle pour le prochain mouvement. En continuant la répétition, nous abaisserons C jusqu'à ce que, espérons-le, nous atteignions un minimum mondial.

En résumé, la descente du gradient passe par un calcul séquentiel du gradient ∇ C et un déplacement ultérieur dans la direction opposée, ce qui conduit à une «chute» le long de la pente de la vallée. Cela peut être visualisé comme suit: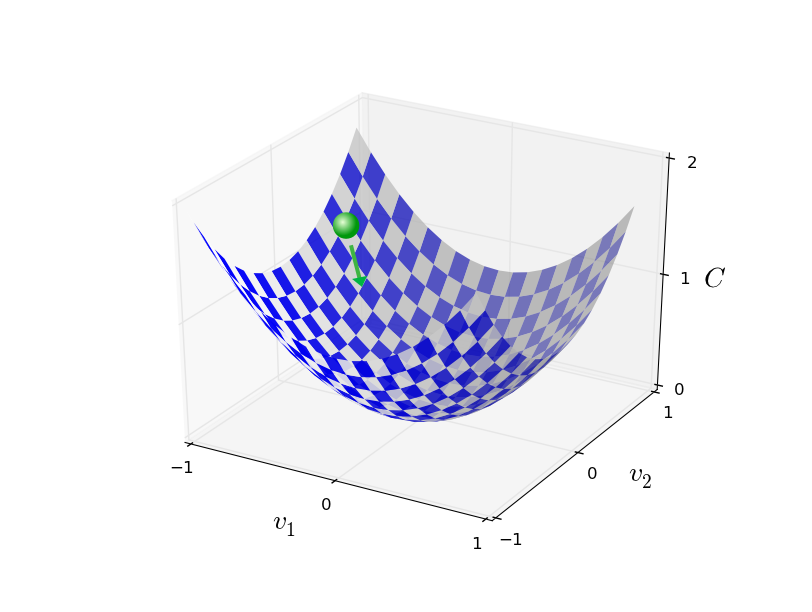



Notez qu'avec cette règle, la descente en gradient ne reproduit pas le mouvement physique réel. Dans la vraie vie, le ballon a une impulsion qui peut lui permettre de rouler sur la pente, ou même de rouler pendant un certain temps. Ce n'est qu'après le travail de la force de friction que la balle est garantie de rouler dans la vallée. Notre règle de sélection Δv dit simplement «descendre». Une assez bonne règle pour trouver le minimum!

Pour que la descente de gradient fonctionne correctement, nous devons choisir une valeur suffisamment petite de la vitesse d'apprentissage η pour que l'équation (9) soit une bonne approximation. Sinon, il se peut que ΔC> 0 - rien de bon! En même temps, il n'est pas nécessaire que η soit trop petit, car alors les changements dans Δv seront minuscules et l'algorithme fonctionnera trop lentement. En pratique, η change de sorte que l'équation (9) donne une bonne approximation, et l'algorithme ne fonctionne pas trop lentement. Plus tard, nous verrons comment cela fonctionne.

J'ai expliqué la descente du gradient lorsque la fonction C ne dépendait que de deux variables. Mais tout fonctionne de la même manière si C est fonction de nombreuses variables. Supposons qu'elle ait m variables, v ₁ , ..., v _m. Alors le changement de ΔC provoqué par un petit changement de Δv = (Δv ₁ , ..., Δv _m ) ^T sera

$$

$$\Delta C \approx \nabla C \cdot \Delta v \tag{12}$$

où le gradient ∇C est le vecteur

$$

$$\nabla C \equiv (\frac{\partial C}{\partial v_1},…, \frac{\partial C}{\partial v_m})^T \tag{13}$$

Comme pour deux variables, on peut choisir

$$

$$\Delta v = - \eta \nabla C \tag{14}$$

et assurez-vous que notre expression approximative (12) pour ΔC est négative. Cela nous donne un moyen d'aller le long du gradient au minimum, même lorsque C est une fonction de nombreuses variables, en appliquant la règle de mise à jour encore et encore.

$$

$$v \rightarrow v' = v - \eta \nabla C \tag{15}$$

Cette règle de mise à jour peut être considérée comme l'algorithme définissant la descente de gradient. Cela nous donne une méthode pour changer à plusieurs reprises la position de v à la recherche du minimum de la fonction C.Cette règle ne fonctionne pas toujours - plusieurs choses peuvent mal tourner, empêchant la descente de gradient de trouver le minimum global de C - nous reviendrons sur ce point dans les chapitres suivants. Mais en pratique, la descente en pente fonctionne souvent très bien, et nous verrons qu'à l'Assemblée nationale, c'est un moyen efficace de minimiser la fonction de coût, et donc de former le réseau.

Dans un sens, la descente de gradient peut être considérée comme la stratégie de recherche minimale optimale. Supposons que nous essayons de déplacer Δv vers une position pour minimiser C. Ceci équivaut à minimiser ΔC ≈ ∇C ⋅ Δv. Nous limiterons la taille du pas pour que || Δv || = ε pour une petite constante ε> 0. En d'autres termes, nous voulons déplacer une petite distance d'une taille fixe, et essayer de trouver la direction du mouvement qui diminue autant que possible C. On peut prouver que le choix de Δv minimisant ∇C ⋅ Δv est Δv = -η∇C, où η = ε / || ∇C || est déterminé par la restriction || Δv || = ε. La descente en pente peut donc être considérée comme un moyen de faire de petits pas dans la direction qui diminue le plus C.

Exercices

• . : — , , , .
• , , . , ? ?

Les gens ont étudié de nombreuses options de descente en pente, y compris celles qui reproduisent avec plus de précision une vraie balle physique. De telles options ont leurs avantages, mais aussi un gros inconvénient: la nécessité de calculer les deuxièmes dérivées partielles de C, qui peuvent consommer beaucoup de ressources. Pour comprendre cela, supposons que nous devons calculer toutes les dérivées partielles secondes ∂ ² C / ∂v _j ∂v _k . Si les variables sont v _j million, alors nous devons calculer environ un billion (un million au carré) de dérivées partielles secondaires (en fait, un demi-billion, puisque ∂ ² C / ∂v _j ∂v _k = ∂ ² C / ∂v _k ∂v _j. Mais vous avez saisi l'essence). Cela nécessitera beaucoup de ressources informatiques. Il existe des astuces pour éviter cela, et la recherche d'alternatives à la descente en gradient est un domaine de recherche active. Cependant, dans ce livre, nous utiliserons la descente de gradient et ses variantes comme approche principale de l'apprentissage de la NS.

Comment appliquer la descente de gradient à l'apprentissage NA? Nous devons l'utiliser pour rechercher des poids w _k et des décalages b _l qui minimisent l'équation de coût (6). Réécrivons la règle de mise à jour de la descente de gradient en remplaçant les variables v _j par des poids et des décalages. En d'autres termes, maintenant notre «position» a les composantes w _k et b _l , et le vecteur de gradient ∇C a les composantes correspondantes ∂C / ∂w_k et ∂C / ∂b _l . Après avoir écrit notre règle de mise à jour avec de nouveaux composants, nous obtenons:

$$

$$w_k \rightarrow w'_k = w_k - \eta \frac{\partial C}{\partial w_k} \tag{16}$$

$$

$$b_l \rightarrow b'_l = b_l - \eta \frac{\partial C}{\partial b_l} \tag{17}$$

En réappliquant cette règle de mise à jour, nous pouvons «rouler en descente» et, avec un peu de chance, trouver la fonction de coût minimum. En d'autres termes, cette règle peut être utilisée pour former l'Assemblée nationale.

Il existe plusieurs obstacles à l'application de la règle de descente en pente. Nous les étudierons plus en détail dans les chapitres suivants. Mais pour l'instant, je veux mentionner un seul problème. Pour le comprendre, revenons à la valeur quadratique de l'équation (6). Notez que cette fonction de coût ressemble à C = 1 / n ∑ _x C _x , c'est-à-dire que c'est le coût moyen C _x ≡ (|| y (x) −a || ² ) / 2 pour les exemples de formation individuels. En pratique, pour calculer le gradient ∇C, nous devons calculer les gradients ∇C _x séparément pour chaque entrée d'apprentissage x, puis les faire la moyenne, ∇C = 1 / n ∑ _x ∇C _x . Malheureusement, lorsque la quantité d'entrée sera très importante, cela prendra très longtemps et une telle formation sera lente.

Pour accélérer l'apprentissage, vous pouvez utiliser la descente de gradient stochastique. L'idée est de calculer approximativement le gradient ∇C en calculant ∇C _x pour un petit échantillon aléatoire d'entrée d'entraînement. En calculant leur moyenne, nous pouvons rapidement obtenir une bonne estimation du vrai gradient ∇C, ce qui permet d'accélérer la descente du gradient, et donc l'entraînement.

Formuler plus précisément, la descente de gradient stochastique fonctionne par échantillonnage aléatoire d'un petit nombre de m données d'entrée d'entraînement. Nous appellerons ces données aléatoires X ₁ , X ₂ , .., X _m , et l'appellerons un mini-paquet. Si la taille de l'échantillon m est suffisamment grande, la valeur moyenne de ∇C _{X j} sera suffisamment proche de la moyenne de tous les ∇Cx, c'est-à-dire

$$

$$\ frac {\ sum ^ m_ {j = 1} \ nabla C_ {X_j}} {m} \ approx \ frac {\ sum_x \ nabla C_x} {n} = \ nabla C \ tag {18}$$

où le deuxième montant va sur l'ensemble des données d'entraînement. En échangeant des pièces, nous obtenons

$$

$$\ nabla C \ approx \ frac {1} {m} \ sum ^ m_ {j = 1} \ nabla C_ {X_j} \ tag {19}$$

ce qui confirme que nous pouvons estimer le gradient global en calculant les gradients pour un mini-pack sélectionné au hasard.

Pour relier cela directement à la formation de NS, supposons que w _k et b _l désignent les poids et les déplacements de notre NS. Ensuite, la descente de gradient stochastique sélectionne un mini-paquet aléatoire de données d'entrée et en apprend

$$

$$w_k \ rightarrow w'_k = w_k - \ frac {\ eta} {m} \ sum_j \ frac {\ partial C_ {X_j}} {\ partial w_k} \ tag {20}$$

$$

$$b_l \ rightarrow b'_l = b_l - \ frac {\ eta} {m} \ sum_j \ frac {\ partial C_ {X_j}} {\ partial b_l} \ tag {21}$$

où est la somme de tous les exemples de formation X _j dans le mini-package actuel. Ensuite, nous sélectionnons un autre mini-package aléatoire et étudions dessus. Et ainsi de suite, jusqu'à épuisement de toutes les données d'entraînement, ce qu'on appelle la fin de l'ère de l'entraînement. En ce moment, nous commençons à nouveau une nouvelle ère d'apprentissage.

Soit dit en passant, il convient de noter que les accords concernant la mise à l'échelle de la fonction de coût et la mise à jour des pondérations et des compensations diffèrent dans un mini-package. Dans l'équation (6), nous avons mis à l'échelle la fonction de coût 1 / n fois. Parfois, les gens omettent 1 / n en additionnant les coûts des exemples de formation individuelle, au lieu de calculer la moyenne. Ceci est utile lorsque le nombre total d'exemples de formation n'est pas connu à l'avance. Cela peut se produire, par exemple, lorsque des données supplémentaires apparaissent en temps réel. De la même manière, les règles de mise à jour des mini-packages (20) et (21) omettent parfois le membre 1 / m devant la somme. Conceptuellement, cela n'affecte rien, car cela équivaut à un changement de la vitesse d'apprentissage η. Cependant, il convient de faire attention lors de la comparaison de diverses œuvres.

Une descente de gradient stochastique peut être considérée comme un vote politique: il est beaucoup plus facile de prélever un échantillon sous la forme d'un mini-package que d'appliquer une descente de gradient à un échantillon complet - tout comme un sondage à la sortie d'un site est plus facile que de mener une élection à part entière. Par exemple, si notre ensemble d'entraînement a une taille de n = 60 000, comme MNIST, et que nous faisons un échantillon d'un mini-paquet de taille m = 10, alors nous accélérerons l'estimation du gradient de 6000 fois! Bien sûr, l'estimation ne sera pas idéale - il y aura des fluctuations statistiques - mais elle n'a pas besoin d'être idéale: nous devons seulement nous déplacer dans la direction qui diminue C, ce qui signifie que nous n'avons pas besoin de calculer le gradient avec précision. En pratique, la descente de gradient stochastique est une technique d'enseignement courante et puissante pour l'Assemblée nationale, et la base de la plupart des technologies pédagogiques que nous développerons dans le cadre du livre.

Exercices

• La version extrême de la descente en gradient utilise une taille de mini-paquet de 1. Autrement dit, avec l'entrée x, nous mettons à jour nos poids et décalages selon les règles w _k → w ′ _k = w _k - η ∂C _x / ∂w _k et b _l → b ′ _L = b _l - η ∂C _x / ∂b _l . Ensuite, nous sélectionnons un autre exemple d'entrée d'entraînement et actualisons à nouveau les poids et les décalages. Et ainsi de suite. Cette procédure est appelée apprentissage en ligne ou incrémentiel. Dans l'apprentissage en ligne, NS étudie sur la base d'une copie de formation des données d'entrée à la fois (comme les personnes). Quels sont les avantages et les inconvénients de l'apprentissage en ligne par rapport à la descente de gradient stochastique avec une taille de mini-paquet de 20?

Permettez-moi de terminer cette section par une discussion sur un sujet qui dérange parfois les personnes qui ont d'abord rencontré une descente en pente. En NS, la valeur de C est fonction de nombreuses variables - tous les poids et décalages - et, en un sens, détermine la surface dans un espace très multidimensionnel. Les gens commencent à penser: "Je vais devoir visualiser toutes ces dimensions supplémentaires." Et ils commencent à s'inquiéter: "Je ne peux pas naviguer en quatre dimensions, sans parler de cinq (ou cinq millions)." Ont-ils une qualité particulière que possèdent les «vraies» supermathématiques? Bien sûr que non. Même les mathématiciens professionnels ne peuvent pas très bien visualiser l'espace à quatre dimensions - voire pas du tout. Ils vont à des tours, développant d'autres façons de représenter ce qui se passe. C'est exactement ce que nous avons fait: nous avons utilisé la représentation algébrique (plutôt que visuelle) de ΔC pour comprendre comment se déplacer afin que C diminue. Les gens qui font du bon travail avec un grand nombre de dimensions ont en tête une large bibliothèque de techniques similaires; notre astuce algébrique n'est qu'un exemple. Ces techniques ne sont peut-être pas aussi simples que ce à quoi nous sommes habitués lorsque nous visualisons trois dimensions, mais lorsque vous créez une bibliothèque de techniques similaires, vous commencez à bien réfléchir dans des dimensions plus élevées. Je n'entrerai pas dans les détails, mais si vous êtes intéressé, vous aimerez peut-être la discussion de certaines de ces techniques par des mathématiciens professionnels qui ont l'habitude de penser dans des dimensions plus élevées. Bien que certaines des techniques discutées soient assez complexes, la plupart des meilleures réponses sont intuitives et accessibles à tous.

Mise en place d'un réseau de classification des numéros

Ok, écrivons maintenant un programme qui apprend à reconnaître les chiffres manuscrits en utilisant la descente de gradient stochastique et les données d'entraînement du MNIST. Nous le ferons avec un programme court en python 2.7 composé de seulement 74 lignes! La première chose dont nous avons besoin est de télécharger les données du MNIST. Si vous utilisez git, vous pouvez les obtenir en clonant le référentiel de ce livre:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git

Sinon, téléchargez le code à partir du lien .

Soit dit en passant, lorsque j'ai mentionné les données du MNIST plus tôt, j'ai dit qu'elles étaient divisées en 60 000 images d'entraînement et 10 000 images de test. Ceci est la description officielle du MNIST. Nous allons casser les données un peu différemment. Nous laisserons les images de vérification inchangées, mais nous diviserons l'ensemble de formation en deux parties: 50 000 images, que nous utiliserons pour former l'Assemblée nationale, et 10 000 images individuelles pour confirmation supplémentaire. Bien que nous ne les utiliserons pas, mais plus tard, ils nous seront utiles lorsque nous comprendrons la configuration de certains hyper paramètres de la NS - la vitesse d'apprentissage, etc., - que notre algorithme ne sélectionne pas directement. Bien que les données de corroboration ne fassent pas partie de la spécification MNIST d'origine, beaucoup utilisent MNIST de cette manière, et dans le domaine des HC, l'utilisation de données de corroboration est courante. Maintenant, en parlant des «données de formation du MNIST», je parlerai de nos 50 000 karitnoks, pas des 60 000 originaux.

En plus des données MNIST, nous avons également besoin d'une bibliothèque python appelée Numpy pour des calculs rapides d'algèbre linéaire. Si vous ne l'avez pas, vous pouvez le prendre à partir du lien .

Avant de vous donner tout le programme, laissez-moi vous expliquer les principales caractéristiques du code pour NS. La place centrale est occupée par la classe Réseau, que nous utilisons pour représenter l'Assemblée nationale. Voici le code d'initialisation de l'objet Network:

 class Network(object): def __init__(self, sizes): self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] 

Le tableau des tailles contient le nombre de neurones dans les couches correspondantes. Donc, si nous voulons créer un objet réseau avec deux neurones dans la première couche, trois neurones dans la deuxième couche et un neurone dans la troisième, alors nous l'écrirons comme ceci:

 net = Network([2, 3, 1]) 

Les décalages et les poids de l'objet Réseau sont initialisés de manière aléatoire à l'aide de la fonction numpy np.random.randn, qui génère une distribution gaussienne avec une attente mathématique de 0 et un écart-type de 1. Cette initialisation aléatoire donne à notre algorithme de descente de gradient stochastique un point de départ. Dans les chapitres suivants, nous trouverons les meilleurs moyens d'initialiser les poids et les décalages, mais pour l'instant, cela suffit. Notez que le code d'initialisation du réseau suppose que la première couche de neurones sera entrée et ne leur attribue pas de biais, car ils ne sont utilisés que pour calculer la sortie.

Notez également que les décalages et les poids sont stockés sous forme de tableau de matrices Numpy. Par exemple, net.weights [1] est une matrice Numpy qui stocke les poids reliant les deuxième et troisième couches de neurones (ce ne sont pas les première et deuxième couches, car en python la numérotation des éléments du tableau vient de zéro). Puisqu'il faudra trop de temps pour écrire net.weights [1], nous désignons cette matrice par w. Il s'agit d'une matrice telle que w _jk est le poids de la connexion entre le kième neurone dans la deuxième couche et le jième neurone dans la troisième. Un tel ordre des indices j et k peut sembler étrange - ne serait-il pas plus logique de les échanger? Mais le gros avantage d'un tel record sera que le vecteur d'activation de la troisième couche de neurones est obtenu:

$$

$$a '= \ sigma (wa + b) \ tag {22}$$

Regardons cette équation assez riche. a est le vecteur d'activation de la deuxième couche de neurones. Pour obtenir a ', on multiplie a par la matrice de poids w, et on ajoute le vecteur de déplacement b. Ensuite, nous appliquons l'élément sigmoïde σ élément par élément à chaque élément du vecteur wa + b (c'est ce qu'on appelle la vectorisation de la fonction σ). Il est facile de vérifier que l'équation (22) donne le même résultat que la règle (4) pour le calcul d'un neurone sigmoïde.

Exercice

• Écrivez l'équation (22) sous forme de composant et assurez-vous qu'elle donne le même résultat que la règle (4) pour le calcul d'un neurone sigmoïde.

Avec tout cela à l'esprit, il est facile d'écrire du code qui calcule la sortie d'un objet Network. On commence par définir un sigmoïde:

 def sigmoid(z): return 1.0/(1.0+np.exp(-z)) 

Notez que lorsque le paramètre z est un vecteur ou un tableau Numpy, Numpy appliquera automatiquement le sigmoïde élément par élément, c'est-à-dire sous forme vectorielle.

Ajoutez une méthode de propagation directe à la classe Network, qui prend a du réseau en entrée et renvoie la sortie correspondante. On suppose que le paramètre a est (n, 1) Numdy ndarray, pas un vecteur (n,). Ici n est le nombre de neurones d'entrée. Si vous essayez d'utiliser le vecteur (n,), vous obtiendrez des résultats étranges.

La méthode applique simplement l'équation (22) à chaque couche:

  def feedforward(self, a): """       "a"""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a 

Bien sûr, fondamentalement, nous, des objets réseau, en avons besoin pour apprendre. Pour ce faire, nous leur donnerons la méthode SGD, qui implémente la descente de gradient stochastique. Voici son code. À certains endroits, c'est plutôt mystérieux, mais nous allons l'analyser plus en détail ci-dessous.

  def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): """    -    . training_data –   "(x, y)",       .       .  test_data ,          ,     .     ,    . """ if test_data: n_test = len(test_data) n = len(training_data) for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch(mini_batch, eta) if test_data: print "Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test) else: print "Epoch {0} complete".format(j) 

training_data est une liste de tuples "(x, y)" représentant l'entrée d'entraînement et la sortie souhaitée. Les variables epochs et mini_batch_size sont le nombre d'époques à apprendre et la taille des mini-paquets à utiliser. eta - vitesse d'apprentissage, η. Si test_data est défini, le réseau sera évalué par rapport aux données de vérification après chaque ère et la progression actuelle sera affichée. Ceci est utile pour suivre les progrès, mais ralentit considérablement le travail.

Le code fonctionne comme ceci. À chaque époque, il commence par mélanger accidentellement des données d'entraînement, puis les décompose en mini-paquets de la bonne taille. Il s'agit d'un moyen simple de créer un échantillon de données d'entraînement. Ensuite, pour chaque mini_batch, nous appliquons une étape de descente de gradient. Cela se fait par le code self.update_mini_batch (mini_batch, eta), qui met à jour les pondérations et les décalages du réseau en fonction d'une itération de la descente du gradient en utilisant uniquement les données d'apprentissage dans mini_batch. Voici le code de la méthode update_mini_batch:

  def update_mini_batch(self, mini_batch, eta): """    ,          -. mini_batch –    (x, y),  eta –  .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] 

La plupart du travail est effectué par la ligne.

  delta_nabla_b, delta_nabla_w = self.backprop(x, y) 

Il appelle un algorithme de rétropropagation - un moyen rapide de calculer le gradient d'une fonction de coût. Ainsi, update_mini_batch calcule simplement ces gradients pour chaque exemple de formation à partir de mini_batch, puis met à jour self.weights et self.biases.

Jusqu'à présent, je ne montrerai pas de code pour self.backprop. Nous en apprendrons davantage sur la rétropropagation dans le chapitre suivant, et il y aura du code self.backprop. Pour l'instant, supposons qu'il se comporte comme indiqué, renvoyant un gradient approprié pour le coût associé à l'exemple de formation x.

Regardons l'ensemble du programme, y compris les commentaires explicatifs. À l'exception de la fonction self.backprop, le programme parle de lui-même - le travail principal est effectué par self.SGD et self.update_mini_batch. La méthode self.backprop utilise plusieurs fonctions supplémentaires pour calculer le gradient, à savoir sigmoid_prime, qui calcule la dérivée de sigmoid, et self.cost_derivative, que je ne décrirai pas ici. Vous pouvez vous en faire une idée en consultant le code et les commentaires. Dans le chapitre suivant, nous les examinerons plus en détail. Gardez à l'esprit que même si le programme semble long, la plupart du code est constitué de commentaires qui le rendent plus facile à comprendre. En fait, le programme lui-même ne comprend que 74 non-lignes de code - ni vides ni commentaires. Tout le code est disponible sur GitHub .

 """ network.py ~~~~~~~~~~           .      .     ,    .   ,       . """ ####  #   import random #   import numpy as np class Network(object): def __init__(self, sizes): """  sizes      .  ,      Network      ,     ,     ,    ,  [2, 3, 1].               0    1. ,      ,       ,        . """ self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] def feedforward(self, a): """   ,  ``a`` -  .""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): """    -    . training_data –   "(x, y)",       .       .  test_data ,          ,     .     ,    . """ if test_data: n_test = len(test_data) n = len(training_data) for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch(mini_batch, eta) if test_data: print "Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test) else: print "Epoch {0} complete".format(j) def update_mini_batch(self, mini_batch, eta): """    ,          -. mini_batch –    (x, y),  eta –  .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] def backprop(self, x, y): """  ``(nabla_b, nabla_w)``,      C_x. ``nabla_b``  ``nabla_w`` -    numpy,   ``self.biases`` and ``self.weights``.""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] #   activation = x activations = [x] #      zs = [] #     z- for b, w in zip(self.biases, self.weights): z = np.dot(w, activation)+b zs.append(z) activation = sigmoid(z) activations.append(activation) #   delta = self.cost_derivative(activations[-1], y) * \ sigmoid_prime(zs[-1]) nabla_b[-1] = delta nabla_w[-1] = np.dot(delta, activations[-2].transpose()) """ l      ,      . l = 1    , l = 2 – ,   .    ,   python      .""" for l in xrange(2, self.num_layers): z = zs[-l] sp = sigmoid_prime(z) delta = np.dot(self.weights[-l+1].transpose(), delta) * sp nabla_b[-l] = delta nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) return (nabla_b, nabla_w) def evaluate(self, test_data): """    ,      .    –          .""" test_results = [(np.argmax(self.feedforward(x)), y) for (x, y) in test_data] return sum(int(x == y) for (x, y) in test_results) def cost_derivative(self, output_activations, y): """    ( C_x /  a)   .""" return (output_activations-y) ####   def sigmoid(z): """.""" return 1.0/(1.0+np.exp(-z)) def sigmoid_prime(z): """ .""" return sigmoid(z)*(1-sigmoid(z)) 

Dans quelle mesure le programme reconnaît-il les nombres manuscrits? Commençons par charger les données MNIST. Nous le ferons en utilisant le petit programme d'aide mnist_loader.py, que je décrirai ci-dessous. Exécutez les commandes suivantes dans le shell python:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Bien sûr, cela peut être fait dans un programme séparé, mais si vous travaillez en parallèle avec un livre, ce sera plus facile.

Après avoir téléchargé les données du MNIST, configurez un réseau de 30 neurones cachés. Nous le ferons après avoir importé le programme décrit ci-dessus, appelé réseau:

 >>> import network >>> net = network.Network([784, 30, 10]) 

Enfin, nous utilisons la descente de gradient stochastique pour la formation sur les données de formation pour 30 époques, avec une taille de mini-paquet de 10 et une vitesse d'apprentissage de η = 3,0:

 >>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data) 

Si vous exécutez du code en parallèle avec la lecture d'un livre, gardez à l'esprit qu'il faudra plusieurs minutes pour l'exécuter. Je vous suggère de tout démarrer, de continuer à lire et de vérifier périodiquement ce que le programme produit. Si vous êtes pressé, vous pouvez réduire le nombre d'époques en réduisant le nombre de neurones cachés ou en n'utilisant qu'une partie des données d'entraînement. Le code de travail final fonctionnera plus rapidement: ces scripts python sont conçus pour vous faire comprendre le fonctionnement du réseau et ne sont pas performants! Et, bien sûr, après la formation, le réseau peut fonctionner très rapidement sur presque toutes les plates-formes informatiques. Par exemple, lorsque nous enseignons au réseau une bonne sélection de poids et de compensations, il peut être facilement porté pour fonctionner sur JavaScript dans un navigateur Web ou en tant qu'application native sur un appareil mobile. Dans tous les cas, approximativement la même conclusion est tirée par le programme qui forme le réseau neuronal. Elle écrit le nombre d'images de test correctement reconnues après chaque période de formation. Comme vous pouvez le voir, même après une ère, il atteint une précision de 9 129 sur 10 000, et ce nombre continue de croître:

Epoch 0: 9129 / 10000
Epoch 1: 9295 / 10000
Epoch 2: 9348 / 10000
...
Epoch 27: 9528 / 10000
Epoch 28: 9542 / 10000
Epoch 29: 9534 / 10000

Il s'avère que le réseau formé donne un pourcentage de classement correct d'environ 95 à 95,42% au maximum! Une première tentative assez prometteuse. Je vous préviens que votre code ne produira pas nécessairement exactement les mêmes résultats, car nous initialisons le réseau avec des pondérations et des décalages aléatoires. Pour ce chapitre, j'ai choisi le meilleur des trois essais.

Reprenons l'expérience en changeant le nombre de neurones cachés à 100. Comme précédemment, si vous exécutez le code en même temps que la lecture, gardez à l'esprit que cela prend beaucoup de temps (sur ma machine, chaque époque prend plusieurs dizaines de secondes), il est donc préférable de lire en parallèle avec l'exécution de code.

 >>> net = network.Network([784, 100, 10]) >>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data) 

Naturellement, cela améliore le résultat à 96,59%. Au moins dans ce cas, l'utilisation de plus de neurones cachés aide à obtenir de meilleurs résultats.

Les commentaires des lecteurs suggèrent que les résultats de cette expérience varient considérablement et que certains résultats d'apprentissage sont bien pires. Utiliser les techniques du chapitre 3 pour réduire sérieusement la diversité de l'efficacité du travail d'une exécution à l'autre.

Bien sûr, pour atteindre une telle précision, j'ai dû choisir un certain nombre d'époques d'apprentissage, la taille du mini-package et la vitesse d'apprentissage η. Comme je l'ai mentionné ci-dessus, ils sont appelés hyperparamètres de notre Assemblée nationale - pour les distinguer des paramètres simples (poids et décalages) que l'algorithme ajuste pendant l'entraînement. Si nous choisissons mal les hyperparamètres, nous obtiendrons de mauvais résultats. Supposons, par exemple, que nous ayons choisi le taux d'apprentissage η = 0,001:

 >>> net = network.Network([784, 100, 10]) >>> net.SGD(training_data, 30, 10, 0.001, test_data=test_data) 

Les résultats sont beaucoup moins impressionnants:

Epoch 0: 1139 / 10000
Epoch 1: 1136 / 10000
Epoch 2: 1135 / 10000
...
Epoch 27: 2101 / 10000
Epoch 28: 2123 / 10000
Epoch 29: 2142 / 10000

Cependant, vous pouvez voir que l'efficacité du réseau augmente lentement au fil du temps. Cela suggère que vous pouvez essayer d'augmenter la vitesse d'apprentissage, par exemple, à 0,01. Dans ce cas, les résultats seront meilleurs, ce qui indique la nécessité d'augmenter encore la vitesse (si le changement améliore la situation, changez encore!). Si vous le faites plusieurs fois, nous finirons par arriver à η = 1.0 (et parfois même 3.0), ce qui est proche de nos expériences précédentes. Ainsi, bien que nous ayons initialement mal sélectionné les hyperparamètres, au moins nous avons rassemblé suffisamment d'informations pour pouvoir améliorer notre choix de paramètres.

En général, le débogage de NA est une question compliquée. Cela est particulièrement vrai lorsque le choix des hyperparamètres initiaux produit des résultats qui ne dépassent pas le bruit aléatoire. Supposons que nous essayons d'utiliser une architecture réussie de 30 neurones, mais changez la vitesse d'apprentissage à 100,0:

 >>> net = network.Network([784, 30, 10]) >>> net.SGD(training_data, 30, 10, 100.0, test_data=test_data) 

Au final, il s'avère que nous sommes allés trop loin et avons pris trop de vitesse:

Epoch 0: 1009 / 10000
Epoch 1: 1009 / 10000
Epoch 2: 1009 / 10000
Epoch 3: 1009 / 10000
...
Epoch 27: 982 / 10000
Epoch 28: 982 / 10000
Epoch 29: 982 / 10000

Imaginez maintenant que nous abordons cette tâche pour la première fois. Bien sûr, nous savons par les premières expériences qu'il serait bon de réduire la vitesse d'apprentissage. Mais si nous abordions cette tâche pour la première fois, nous n'aurions pas de résultats qui pourraient nous conduire à la bonne solution. Pourrions-nous commencer à penser que nous avons peut-être choisi les mauvais paramètres initiaux pour les poids et les décalages, et qu'il est difficile pour le réseau d'apprendre? Ou peut-être que nous n'avons pas suffisamment de données d'entraînement pour obtenir un résultat significatif? Peut-être n'avons-nous pas attendu assez d'époques? Peut-être qu'un réseau de neurones avec une telle architecture ne peut tout simplement pas apprendre à reconnaître les nombres manuscrits? Peut-être que la vitesse d'apprentissage est trop lente? Lorsque vous abordez la tâche pour la première fois, vous n'avez jamais confiance.

De cela, il vaut la peine d'apprendre une leçon que le débogage NS n'est pas une tâche triviale, et cela, comme la programmation régulière, fait partie de l'art. Vous devez apprendre cet art de débogage afin d'obtenir de bons résultats de NS. En général, nous devons développer une heuristique pour sélectionner de bons hyperparamètres et une bonne architecture. Nous en discuterons en détail dans le livre, y compris comment j'ai sélectionné les hyperparamètres ci-dessus.

Exercice

• Essayez de créer un réseau de seulement deux couches - entrée et sortie, sans caché - avec 784 et 10 neurones, respectivement. Former le réseau avec une descente de gradient stochastique. Quelle précision de classification obtenez-vous?

J'ai précédemment ignoré les détails du chargement des données MNIST. Cela arrive tout simplement. Voici le code pour compléter l'image. Les structures de données sont décrites dans les commentaires - tout est simple, des tuples et des tableaux d'objets ndarray Numpy (si vous n'êtes pas familier avec de tels objets, imaginez-les comme des vecteurs).

 """ mnist_loader ~~~~~~~~~~~~      MNIST.       ``load_data``  ``load_data_wrapper``.  , ``load_data_wrapper`` -  ,     . """ ####  #  import cPickle import gzip #  import numpy as np def load_data(): """  MNIST   ,  ,    . ``training_data``      .    .  numpy ndarray  50 000 .   –     numpy ndarray  784 ,  28 * 28 = 784    MNIST.  –  numpy ndarray  50 000 .   –   0  9   ,    . ``validation_data``  ``test_data`` ,    10 000 .    ,           ``training_data``.    - ``load_data_wrapper()``. """ f = gzip.open('../data/mnist.pkl.gz', 'rb') training_data, validation_data, test_data = cPickle.load(f) f.close() return (training_data, validation_data, test_data) def load_data_wrapper(): """ ,  ``(training_data, validation_data, test_data)``.   ``load_data``,         .  , ``training_data`` -    50 000    , ``(x, y)``. ``x`` -  784- numpy.ndarray,   . ``y`` -  10- numpy.ndarray,   ,     ``x``. ``validation_data``  ``test_data`` -  ,   10 000    , ``(x, y)``. ``x`` -  784- numpy.ndarray,   ,  ``y`` -   ,  ,   ( ),  ``x``. ,  ,           .         .""" tr_d, va_d, te_d = load_data() training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]] training_results = [vectorized_result(y) for y in tr_d[1]] training_data = zip(training_inputs, training_results) validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]] validation_data = zip(validation_inputs, va_d[1]) test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]] test_data = zip(test_inputs, te_d[1]) return (training_data, validation_data, test_data) def vectorized_result(j): """ 10-    1.0   j     .      (0..9)     .""" e = np.zeros((10, 1)) e[j] = 1.0 return e 

J'ai dit que notre programme obtient de très bons résultats. Qu'est-ce que cela signifie? Bon par rapport à quoi? Il est utile d'avoir les résultats de quelques tests simples et de base avec lesquels vous pourriez faire une comparaison pour comprendre ce que signifient de «bons résultats». Le niveau de base le plus simple, bien sûr, serait une supposition aléatoire. Cela peut être fait dans environ 10% des cas. Et nous montrons un bien meilleur résultat!

Qu'en est-il d'un niveau de base moins trivial? Voyons à quel point l'image est sombre. Par exemple, l'image 2 sera généralement plus sombre que l'image 1, simplement parce qu'elle a plus de pixels sombres, comme le montrent les exemples ci-dessous:



Il s'ensuit que nous pouvons calculer l'obscurité moyenne pour chaque chiffre de 0 à 9. Lorsque nous obtenons une nouvelle image, nous calculons son obscurité, et nous supposons qu'elle montre un chiffre avec l'obscurité moyenne la plus proche. Il s'agit d'une procédure simple qui est facile à programmer, donc je n'écrirai pas de code - si cela vous intéresse, il se trouve sur GitHub . Mais c'est une amélioration sérieuse par rapport aux suppositions aléatoires - le code reconnaît correctement 2225 images sur 10000, c'est-à-dire qu'il donne une précision de 22,25%.

Il n'est pas difficile de trouver d'autres idées qui atteignent une précision de 20 à 50%. Après avoir travaillé un peu plus, vous pouvez dépasser 50%. Mais pour obtenir une précision beaucoup plus grande, il est préférable d'utiliser des algorithmes MO faisant autorité. Essayons l'un des algorithmes les plus célèbres, la méthode du vecteur de support ou SVM. Si vous n'êtes pas familier avec SVM, ne vous inquiétez pas, nous n'avons pas besoin de comprendre ces détails. Nous utilisons simplement une bibliothèque python appelée scikit-learn, qui fournit une interface simple à la bibliothèque C rapide pour SVM, connue sous le nom de LIBSVM .

Si nous exécutons le classificateur SVM scikit-learn avec les paramètres par défaut, nous obtenons la classification correcte de 9 435 sur 10 000 (le code est disponible sur le lien) C'est déjà une grande amélioration par rapport à l'approche naïve de classification des images par obscurité. Cela signifie que SVM fonctionne aussi bien que notre NS, mais un peu moins bien. Dans les chapitres suivants, nous nous familiariserons avec de nouvelles techniques qui nous permettront d'améliorer notre NS afin qu'elles surpassent largement SVM.

Mais ce n'est pas tout.Le résultat 9 435 sur 10 000 de scikit-learn est spécifié pour les paramètres par défaut. SVM possède de nombreux paramètres qui peuvent être réglés, et vous pouvez rechercher des paramètres qui améliorent ce résultat. Je n'entrerai pas dans les détails, ils peuvent être lus dans l' article d' Andreas Muller. Il a montré qu'en effectuant des travaux pour optimiser les paramètres, il est possible d'atteindre une précision d'au moins 98,5%. En d'autres termes, un SVM bien réglé ne fait qu'un seul chiffre sur 70 erreurs, un bon résultat! NA peut-il faire plus?

Il s'avère qu'ils le peuvent. Aujourd'hui, une NS bien réglée dépasse toute autre technologie connue de la solution MNIST, y compris SVM. Record pour 2013correctement classé 9 979 images sur 10 000. Et nous verrons la plupart des technologies utilisées pour cela dans ce livre. Ce niveau de précision est proche de l'humain, et peut-être même le dépasse, car plusieurs images du MNIST sont difficiles à déchiffrer même pour l'homme, par exemple: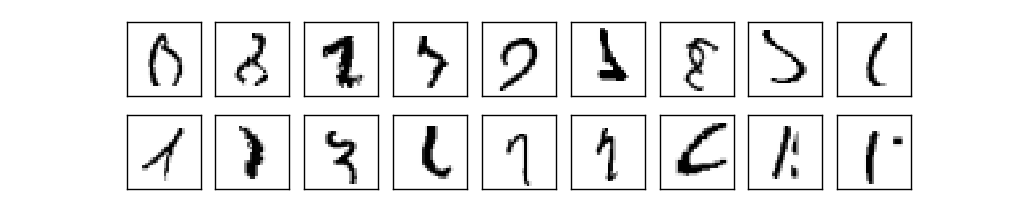



je pense que vous conviendrez qu'il est difficile de les classer! Avec de telles images dans le jeu de données MNIST, il est surprenant que le NS puisse reconnaître correctement toutes les 10 000 images, sauf 21. Habituellement, les programmeurs pensent que résoudre une tâche aussi complexe nécessite un algorithme complexe. Mais même la NS est au travaille détenteur du record utilise des algorithmes assez simples, qui sont de petites variations de ceux que nous avons examinés dans ce chapitre. Toute la complexité apparaît automatiquement pendant l'entraînement en fonction des données d'entraînement. En un sens, la morale de nos résultats et de ceux contenus dans des travaux plus complexes est que pour certaines tâches

algorithme complexe ≤ algorithme d'entraînement simple + bonnes données d'entraînement

Vers l'apprentissage profond

Bien que notre réseau affiche des performances impressionnantes, il est réalisé de manière mystérieuse. Les poids et les réseaux de mélange sont détectés automatiquement. Donc, nous n'avons pas d'explication toute faite sur la façon dont le réseau fait ce qu'il fait. Existe-t-il un moyen de comprendre les principes de base de la classification par un réseau de nombres manuscrits? Et est-il possible, compte tenu d'eux, d'améliorer le résultat?

Nous reformulons ces questions de manière plus stricte: supposons que dans quelques décennies la NS se transformera en intelligence artificielle (IA). Comprendrons-nous comment fonctionne cette IA? Peut-être que les réseaux resteront incompréhensibles pour nous, avec leurs poids et leurs décalages, car ils sont attribués automatiquement. Dans les premières années de la recherche sur l'IA, les gens espéraient qu'essayer de créer l'IA nous aiderait également à comprendre les principes qui sous-tendent l'intelligence, et peut-être même le travail du cerveau humain. Cependant, au final, il se peut que nous ne comprenions ni le cerveau ni le fonctionnement de l'IA!

Pour traiter ces questions, rappelons l'interprétation des neurones artificiels que j'ai donnée au début du chapitre - que c'est une façon de peser les preuves. Supposons que nous voulons déterminer si le visage d'une personne est sur une image:







Ce problème peut être abordé de la même manière que la reconnaissance de l'écriture manuscrite: l'utilisation de pixels d'image comme entrée pour la NS, et la sortie de la NS sera un neurone qui dira: «Oui, c'est un visage» ou «Non, ce n'est pas un visage ".

Supposons que nous le fassions, mais sans utiliser d'algorithme d'apprentissage. Nous essaierons de créer manuellement un réseau, en choisissant les poids et décalages appropriés. Comment pouvons-nous aborder cela? Un instant, oubliant l'Assemblée nationale, on pourrait diviser la tâche en sous-tâches: l'image des yeux a-t-elle dans le coin supérieur gauche? Y a-t-il un œil dans le coin supérieur droit? Y a-t-il un nez moyen? Y a-t-il une bouche au milieu? Y a-t-il des cheveux au sommet? Et ainsi de suite.

Si les réponses à plusieurs de ces questions sont positives, voire «probablement oui», alors nous concluons que l'image peut avoir un visage. Inversement, si les réponses sont non, alors il n'y a probablement personne.

Ceci, bien sûr, est une heuristique approximative et présente de nombreuses lacunes. C'est peut-être un homme chauve, et il n'a pas de cheveux. Peut-être que nous ne pouvons voir qu'une partie du visage, ou le visage à un angle, de sorte que certaines parties du visage sont fermées. Néanmoins, l'heuristique suggère que si nous pouvons résoudre des sous-problèmes à l'aide de réseaux de neurones, alors nous pouvons peut-être créer des NS pour la reconnaissance faciale en combinant des réseaux pour des sous-tâches. Ce qui suit est une architecture possible d'un tel réseau dans lequel les sous-réseaux sont indiqués par des rectangles. Ce n'est pas une approche complètement réaliste pour résoudre le problème de reconnaissance faciale: elle est nécessaire pour nous aider à comprendre intuitivement le travail des réseaux de neurones.


Dans les rectangles, il y a des sous-tâches: l'image des yeux a-t-elle dans le coin supérieur gauche? Y a-t-il un œil dans le coin supérieur droit? Y a-t-il un nez moyen? Y a-t-il une bouche au milieu? Y a-t-il des cheveux au sommet? Et ainsi de suite.

Il est possible que des sous-réseaux puissent également être désassemblés en composants. Prenez la question d'avoir un œil dans le coin supérieur gauche. Il peut être distingué en des questions telles que: "Y a-t-il un sourcil?", "Y a-t-il des cils?", "Y a-t-il un élève?" et ainsi de suite. Bien sûr, les questions doivent contenir des informations sur l'emplacement - "Le sourcil est-il situé en haut à gauche, au-dessus de la pupille?", Etc. - mais simplifions pour l'instant. Par conséquent, le réseau qui répond à la question de la présence de l'œil peut être démonté en composantes:


«Y a-t-il un sourcil?», «Y a-t-il des cils?», «Y a-t-il une pupille?»

Ces questions peuvent être décomposées en petites questions, par étapes à travers de nombreuses couches. En conséquence, nous travaillerons avec des sous-réseaux qui répondent à des questions si simples qu'ils peuvent être facilement démontés au niveau des pixels. Ces questions peuvent concerner, par exemple, la présence ou l'absence de formes simples à certains endroits de l'image. Les neurones individuels associés aux pixels pourront y répondre.

Le résultat est un réseau qui décompose des questions très complexes - si une personne est dans l'image - en questions très simples auxquelles il est possible de répondre au niveau de chaque pixel. Elle le fera à travers une séquence de plusieurs couches, dans laquelle les premières couches répondent à des questions très simples et spécifiques sur l'image, et ces dernières créent une hiérarchie de concepts plus complexes et abstraits. Les réseaux avec une telle structure multicouche - deux couches cachées ou plus - sont appelés réseaux de neurones profonds (GNS).

Bien sûr, je n'ai pas parlé de la façon de faire ce sous-réseau récursif. Il sera certainement impossible de sélectionner manuellement les poids et les décalages. Nous aimerions utiliser des algorithmes de formation pour que le réseau apprenne automatiquement les poids et les décalages - et à travers eux les hiérarchies de concepts - sur la base des données de formation. Dans les années 1980 et 1990, des chercheurs ont tenté d'utiliser la descente et la rétropropagation à gradient stochastique pour entraîner le GNS. Malheureusement, à l'exception de quelques architectures spéciales, elles n'ont pas réussi. Les réseaux se sont entraînés, mais très lentement, et dans la pratique, il était trop lent pour être utilisé d'une manière ou d'une autre.

Depuis 2006, plusieurs technologies ont été développées pour former les STS. Ils sont basés sur la descente et la propagation de gradient stochastique, mais ils contiennent également de nouvelles idées. Ils ont permis de former des réseaux beaucoup plus profonds - aujourd'hui, les gens forment tranquillement des réseaux à 5-10 couches. Et il s'avère qu'ils résolvent de nombreux problèmes bien mieux que les NS peu profonds, c'est-à-dire les réseaux avec une couche cachée. La raison, bien sûr, est que STS peut créer une hiérarchie complexe de concepts. Ceci est similaire à la façon dont les langages de programmation utilisent des schémas modulaires et des idées d'abstraction pour pouvoir créer des programmes informatiques complexes. Comparer un NS profond avec un NS peu profond, c'est approximativement comment comparer un langage de programmation qui peut effectuer des appels de fonction avec un langage qui ne le fait pas. L'abstraction dans la NS ne ressemble pas aux langages de programmation,mais a la même importance.