Qu'il y ait une expérience abstraite au cours de laquelle un certain événement peut se produire. Cette expérience a été réalisée cinq fois, et dans quatre d'entre eux, le même événement a eu lieu. Quelles conclusions peut-on tirer de ces 4/5?

Il
existe une formule de Bernoulli qui donne la réponse avec quelle probabilité 4 sur 5 se produisent avec une probabilité initiale connue. Mais elle ne donne pas de réponse, quelle était la probabilité initiale si les événements s'avéraient être 4 sur 5. Laissons de côté la formule de Bernoulli.
Nous allons créer un petit programme simple qui simule les processus de probabilité pour un tel cas, et sur la base du résultat des calculs, nous construisons un graphique.
void test1() { uint sz_ar_events = 50;
Le code de ce programme peut être trouvé
ici , ainsi que les fonctions auxiliaires.
Le calcul a été jeté dans Excel et fait un calendrier.

Cette version du graphique peut être appelée la distribution de densité de probabilité de la valeur de probabilité. Sa superficie est égale à l'unité qui est distribuée dans ce monticule.
Pour compléter le tableau, je mentionnerai que ce graphique correspond au graphique selon la formule de Bernoulli du paramètre de probabilité et multiplié par N + 1 le nombre d'expériences.
Plus loin dans le texte, où j'utilise une fraction de la forme k / n dans l'article, ce n'est pas une division, ce sont k événements de n expériences, afin de ne pas écrire k de n à chaque fois.
Ensuite. Il est possible d'augmenter le nombre d'expériences et d'obtenir une région plus étroite de l'emplacement des valeurs principales de la valeur de probabilité, mais quelle que soit la façon dont elles sont augmentées, cette région ne sera pas réduite à la région zéro avec une probabilité connue.
Le graphique ci-dessous montre les distributions pour 4/5, 7/9, 11/14 et 24/30. Plus la zone est étroite, plus le monticule est élevé, dont la zone est une unité constante. Ces relations ont été choisies parce qu'elles sont toutes de l'ordre de 0,8, et non pas parce que ce sont précisément celles-ci qui peuvent apparaître à 0,8 de la probabilité initiale. Sélectionné pour démontrer quelle plage de valeurs possibles reste, même avec 30 expériences effectuées.
Le code du programme pour ce graphique est
ici .

D'où il résulte qu'en réalité la probabilité expérimentale ne peut pas être déterminée exactement, mais nous ne pouvons que supposer la région de l'emplacement possible d'une telle quantité, avec une précision dépendant du nombre de mesures prises.
Quel que soit le nombre d'expériences effectuées, il est toujours possible que la probabilité initiale se révèle être à la fois 0,0001 et 0,9999. Par souci de simplicité, des valeurs extrêmement improbables sont ignorées. Et nous prenons, par exemple, 95% de la zone principale du calendrier de distribution.
Une telle chose est appelée intervalles de confiance. Je n'ai rencontré aucune recommandation sur le montant et les raisons pour lesquelles l'intérêt devrait rester. Pour les prévisions météorologiques, prenez moins, pour lancer plus de navettes spatiales. Ils ne mentionnent généralement pas non plus quel intervalle de confiance est néanmoins utilisé pour la probabilité des événements et s'il est utilisé du tout.
Dans mon programme, le calcul des limites de l'intervalle de confiance est effectué
ici .
Il s'est avéré que la probabilité de l'événement est déterminée par la densité de probabilité de la valeur de probabilité, et il est toujours nécessaire de lui imposer un pourcentage de l'aire des valeurs principales afin que vous puissiez au moins dire avec certitude quel type de probabilité est l'événement étudié.
Maintenant, à propos d'une expérience plus réelle.
Laissez tout le monde s'ennuyer avec une pièce, lancez cette pièce et obtenez 4 gouttes sur 5 par pile - un cas très réel. En fait, ce n'est pas tout à fait la même chose que celle décrite un peu plus haut. En quoi est-ce différent de l'expérience précédente?
L'expérience précédente a été décrite en supposant que la probabilité de l'événement peut être également répartie sur l'intervalle de 0 à 1. Dans le programme, cela est spécifié par la ligne
double probabilité = get_random_real_0_1 (); . Mais il n'y a pas de pièces avec une probabilité de chute, disons que 0,1 ou 0,9 sont toujours d'un côté.
Si vous prenez un millier de pièces différentes de l'ordinaire au plus incurvé, et pour chacune mesurez la perte en les jetant mille fois ou plus, alors cela montrera qu'elles tombent vraiment d'un côté dans la plage de 0,4 à 0,6 (ce sont des nombres aléatoires, je ne le ferai pas mais je cherche 1000 pièces et je les lance 1000 fois).
Comment ce fait change-t-il le programme de simulation des probabilités d'une pièce particulière, pour laquelle 4 queues sur 5 ont été reçues?
Supposons que la distribution de la perte d'un côté pour les pièces soit décrite comme une approximation du graphique de la distribution normale prise avec des paramètres moyenne = 0,5, écart type = 0,1. (dans le graphique ci-dessous, il est représenté en noir).
Quand dans un programme je change la génération de la probabilité initiale de répartie également en distribuée selon la règle spécifiée, j'obtiens les graphiques suivants:
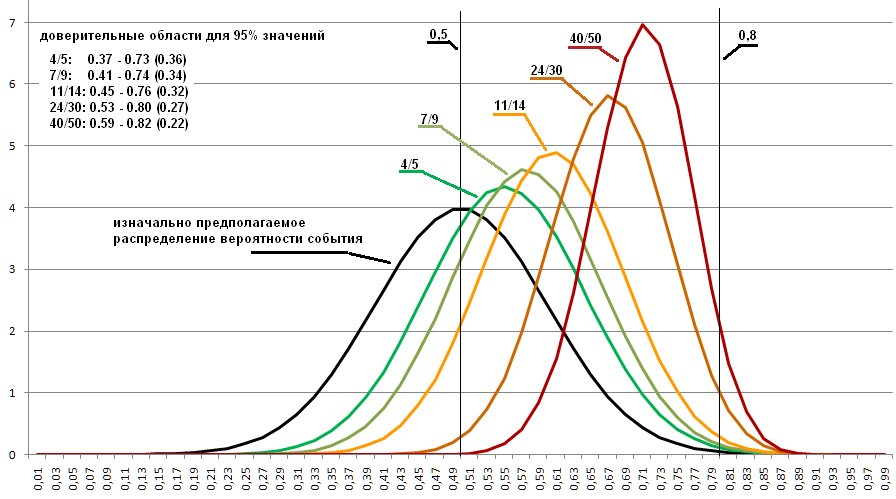
Le code de cette option est
ici .
On peut voir que les distributions ont fortement changé et déterminent maintenant une région légèrement différente dans laquelle la probabilité souhaitée est hautement probable. Par conséquent, si l'on sait quelles probabilités existent pour ces choses, dont l'une que nous voulons mesurer, cela peut quelque peu améliorer le résultat.
En conséquence, 4/5 ne signifie rien, et même 50 des expériences effectuées ne sont pas très informatives. Il s'agit de très peu d'informations pour déterminer le type de probabilité qui sous-tend encore l'expérience.
== Mettre à jour ==
Comme
jzha l'a mentionné dans les commentaires, une personne qui connaît les mathématiques de manière significative, ces graphiques peuvent également être construits en utilisant des formules exactes. Mais le but de cet article est toujours de démontrer aussi clairement que possible comment se forme ce que tout le monde appelle la probabilité.
Afin de le construire en utilisant des formules exactes, il est nécessaire de considérer les données disponibles sur la distribution de probabilité de toutes les pièces à travers l'approximation de la distribution bêta, et en calculant les distributions, dérivez déjà les calculs. Un tel schéma est une quantité substantielle d'explications sur la façon de le faire, et si je le décris ici, il se révélera être un article sur les calculs mathématiques, plutôt que sur les probabilités quotidiennes.
Comment obtenir les formules décrites dans un cas spécial avec une pièce, voir les commentaires de
jzha .