WBOIT en OpenGL: transparence sans tri

Ce message concerne la transparence pondérée indépendante de l'ordre (WBOIT) - l'astuce qui a été abordée dans JCGT en 2013.

Lorsque plusieurs objets transparents apparaissent sur un écran, la couleur des pixels dépend de celui qui est le plus proche du spectateur. Voici un opérateur de mélange bien connu utilisé dans ce cas:

$$

$$\ begin {matrix} C = C_ {near} \ alpha + C_ {far} (1- \ alpha) && (1) \ end {matrix}$$

L'ordre des fragments est important. L'opérateur contient la couleur (C _près ) et l'opacité ( α ) d'un fragment proche et la couleur globale (C _loin ) de tous les fragments derrière lui. L'opacité peut aller de 0 à 1; 0 signifie que l'objet est complètement transparent (invisible) et 1 signifie qu'il est complètement opaque.

Pour utiliser cet opérateur, vous devez trier les fragments par profondeur. Imaginez quelle malédiction c'est. En règle générale, vous devez effectuer un tri par trame. Si vous triez des objets, vous devrez peut-être traiter des surfaces de forme irrégulière qui doivent être coupées en sections, puis les PARTIES coupées de ces surfaces doivent être triées (vous devez absolument le faire pour les surfaces qui se croisent). Si vous triez des fragments, vous allez placer le tri réel dans vos shaders. Cette méthode est connue sous le nom de «transparence indépendante de l'ordre» (OIT), et elle est basée sur une liste liée stockée dans la mémoire vidéo. Il est presque impossible de prévoir la quantité de mémoire à allouer à cette liste. Et si vous manquez de mémoire, vous obtenez des artefacts à l'écran.

Considérez-vous chanceux si vous pouvez réguler le nombre d'objets transparents sur votre scène et ajuster leurs positions relatives. Mais si vous développez une CAO, il appartient aux utilisateurs de positionner leurs objets, il y aura donc autant d'objets qu'ils le souhaitent et leur placement sera tout à fait arbitraire.

Vous voyez maintenant pourquoi est-il si tentant de trouver un opérateur de fusion qui ne nécessite pas de tri préalable. Et il y a un tel opérateur - dans un document que j'ai mentionné au début. En fait, il existe plusieurs formules, mais l'une d'entre elles, les auteurs (et moi-même) considèrent la meilleure:

$$

$$\ begin {matrix} C = {{\ sum_ {i = 1} ^ {n} C_i \ alpha_i} \ over {\ sum_ {i = 1} ^ {n} \ alpha_i}} (1- \ prod_ {i = 1} ^ {n} (1- \ alpha_i)) + C_0 \ prod_ {i = 1} ^ {n} (1- \ alpha_i) && (2) \ end {matrix}$$

Sur la capture d'écran, on peut voir des groupes de triangles transparents disposés sur quatre couches de profondeur. Sur le côté gauche, ils ont été rendus avec WBOIT, et sur le côté droit, le mélange classique dépendant de l'ordre - avec la formule (1) - a été utilisé (je l'appellerai désormais CODB).

Avant de pouvoir commencer à rendre des objets transparents, nous devons rendre tous les objets non transparents. Après cela, les objets transparents sont rendus avec le test de profondeur mais sans écrire quoi que ce soit dans un tampon de profondeur (cela peut être fait de cette façon: glEnable(GL_DEPTH_TEST); glDepthMask(GL_FALSE); ).

Maintenant, regardons ce qui se passe à un moment donné avec les coordonnées de l'espace écran (x, y). Les fragments transparents - qui se trouvent être plus proches que ceux non transparents - réussissent le test de profondeur, peu importe la façon dont ils sont placés par rapport aux fragments transparents déjà rendus. Ces fragments transparents qui tombent derrière le non transparent - eh bien, ils ne passent pas le test de profondeur et sont jetés, naturellement.

C ₀ dans la formule (2) est la couleur du fragment non transparent rendu en ce point (x, y). Nous avons au total n fragments transparents qui ont réussi le test de profondeur, et ils ont des indices i ∈ [1, n]. C _i est la couleur du ième fragment transparent et α _i est son opacité.

La formule (2) est légèrement similaire à la formule (1), bien qu'elle ne soit pas très évidente. Remplacer avec C _près , C ₀ avec C _loin et avec α et la formule (1) sera exactement ce que vous obtiendrez. En effet, est la moyenne arithmétique pondérée des couleurs de tous les fragments transparents (il existe une formule similaire en mécanique pour le "centre de masse"), et elle ira pour la couleur du fragment _proche C _proche . C ₀ est la couleur du fragment non transparent derrière tous ces fragments transparents pour lesquels nous calculons la moyenne arithmétique pondérée. En d'autres termes, nous remplaçons tous les fragments transparents par un fragment "moyenne pondérée" et utilisons l'opérateur de mélange standard - formule (1). Maintenant, il existe une formule un peu sophistiquée pour α , et nous n'avons pas encore compris sa signification.

$$

$$\ alpha = 1- \ prod_ {i = 1} ^ {n} (1- \ alpha_i)$$

C'est une fonction scalaire dans un espace à n dimensions. Tous les α _i sont contenus dans [0, 1], donc sa dérivée partielle par rapport à l'un des α _i est une constante non négative. Cela signifie que l'opacité du fragment "moyenne pondérée" augmente lorsque vous augmentez l'opacité de l'un des fragments transparents, ce qui est exactement ce que nous voulons. De plus, il augmente linéairement.

Si l'opacité d'un fragment est égale à 0, elle est complètement invisible. Cela ne contribue pas du tout à la couleur résultante.

Si au moins un fragment a une opacité de 1, alors α vaut également 1. Autrement dit, un fragment non transparent devient invisible, ce qui est bien. Le problème est que les autres fragments transparents (derrière ce fragment avec opacité = 1) peuvent toujours être vus à travers lui et contribuent à la couleur résultante:



Le triangle orange sur cette image se trouve en haut, le triangle vert en dessous et en dessous du triangle vert se trouvent des triangles gris et cyan. Le fond est noir. L'opacité du triangle orange est de 1; tous les autres ont une opacité = 0,5. Ici, vous pouvez voir que WBOIT semble très pauvre. Le seul endroit où la vraie couleur orange apparaît est le bord du triangle vert délimité par une ligne blanche non transparente. Comme je viens de le mentionner, un fragment non transparent est invisible s'il a un fragment transparent au-dessus avec une opacité = 1.

On le voit mieux sur la photo suivante:



L'opacité du triangle orange est 1, le triangle vert avec la transparence désactivée est juste rendu avec des objets non transparents. Il ressemble à la couleur VERTE du triangle derrière le tamis à travers le triangle supérieur en tant que couleur ORANGE.

Le moyen le plus simple de rendre votre image plausible est de ne pas définir une opacité élevée pour vos objets. Dans un projet où j'utilise cette technique, je ne fixe pas d'opacité supérieure à 0,5. Il s'agit de CAD 3D où les objets sont dessinés schématiquement et n'ont pas besoin d'être très réalistes, cette restriction est donc acceptable.

Avec de faibles opacités, les images gauche et droite sont très similaires:



Et ils diffèrent sensiblement avec des opacités élevées:



Voici un polyèdre transparent:




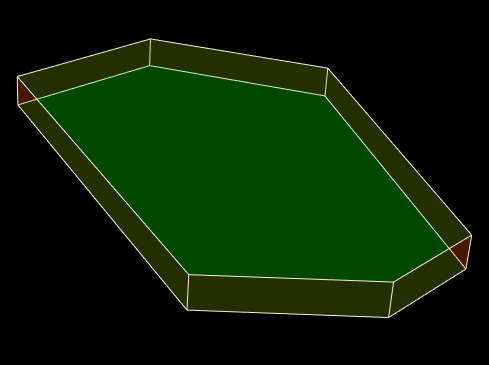
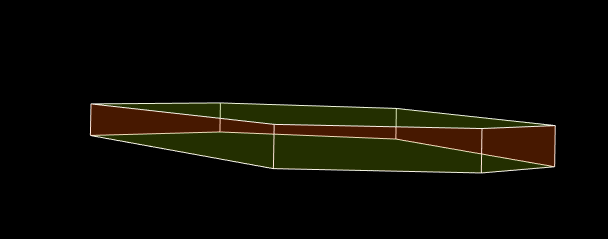
Il a des faces latérales orange et des faces horizontales vertes, ce qui n'est malheureusement pas évident, ce qui signifie que l'image ne semble pas crédible. Partout où un visage orange se trouve au-dessus, la couleur doit être plus orange, et là où elle se trouve derrière un visage vert, la couleur doit être plus verte. Mieux vaut les dessiner avec une seule couleur:

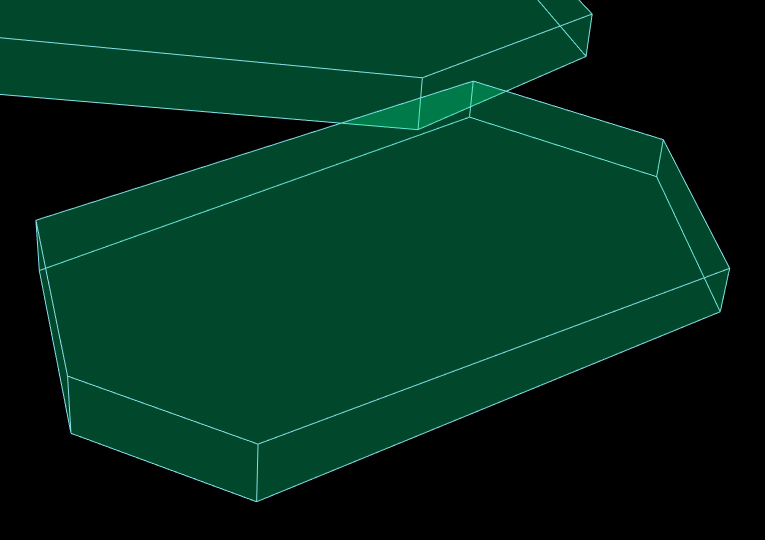
Injecter de la profondeur dans l'opérateur de mélange

Afin de compenser le manque de tri en profondeur, les auteurs du document JCGT susmentionné ont proposé plusieurs façons d'injecter de la profondeur dans la formule (2). Cela complique la mise en œuvre et rend le résultat moins prévisible. Pour que cela fonctionne, les paramètres de fusion doivent être ajustés en fonction d'une scène 3D spécifique. Je n'ai pas approfondi ce sujet, donc si vous voulez en savoir plus, lisez l'article.

Les auteurs affirment que parfois WBOIT est capable de faire quelque chose que CODB ne peut pas faire. Par exemple, envisagez de dessiner une fumée comme un système de particules avec deux particules: la fumée sombre et la fumée plus claire. Lorsque les particules se déplacent et qu'une particule en traverse une autre, leur couleur mélangée passe instantanément de l'obscurité à la lumière, ce qui n'est pas bon. L'opérateur WBOIT avec profondeur produit un résultat plus préférable avec une transition en douceur de la couleur. Les cheveux ou la fourrure modélisés comme un ensemble de tubes fins ont la même propriété.

Le code

Passons maintenant à l'implémentation OpenGL de la formule (2). Vous pouvez voir l'implémentation sur GitHub. C'est une application basée sur Qt, et les images que vous voyez ici en sont principalement issues.

Si vous êtes nouveau dans le rendu transparent, voici un bon matériel d'entrée de gamme:
Apprenez OpenGL. Mélange

Je recommande de le lire avant de poursuivre avec ce post.

Afin d'évaluer la formule (2), nous avons besoin de 2 tampons d'image supplémentaires, de 3 textures multisamles et d'un tampon de rendu de profondeur. Les objets non transparents seront rendus dans la première texture, colorTextureNT. Son type est GL_RGB10_A2. La deuxième texture (colorTexture) sera de type GL_RGBA16F. 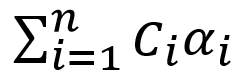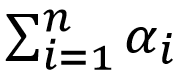Les trois premiers composants de colorTexture contiendront cette partie de la formule (2): et sera écrit dans le quatrième composant. La dernière texture, alphaTexture, de type GL_R16 contiendra .

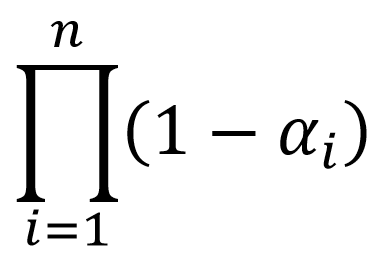
Tout d'abord, nous devons créer tous ces objets et obtenir leurs identifiants à partir d'OpenGL:

  f->glGenFramebuffers (1, &framebufferNT ); f->glGenTextures (1, &colorTextureNT ); f->glGenRenderbuffers(1, &depthRenderbuffer); f->glGenFramebuffers(1, &framebuffer ); f->glGenTextures (1, &colorTexture); f->glGenTextures (1, &alphaTexture); 

J'utilise Qt framewok, comme vous vous en souvenez, et tous les appels à OpenGL sont effectués à partir d'un objet de type QOpenGLFunctions_4_5_Core, pour lequel j'utilise toujours le nom f.

L'allocation de mémoire vient ensuite:

  f->glBindTexture(GL_TEXTURE_2D_MULTISAMPLE, colorTextureNT); f->glTexImage2DMultisample( GL_TEXTURE_2D_MULTISAMPLE, numOfSamples, GL_RGB16F, w, h, GL_TRUE ); f->glBindRenderbuffer(GL_RENDERBUFFER, depthRenderbuffer); f->glRenderbufferStorageMultisample( GL_RENDERBUFFER, numOfSamples, GL_DEPTH_COMPONENT, w, h ); f->glBindTexture(GL_TEXTURE_2D_MULTISAMPLE, colorTexture); f->glTexImage2DMultisample( GL_TEXTURE_2D_MULTISAMPLE, numOfSamples, GL_RGBA16F, w, h, GL_TRUE ); f->glBindTexture(GL_TEXTURE_2D_MULTISAMPLE, alphaTexture); f->glTexImage2DMultisample( GL_TEXTURE_2D_MULTISAMPLE, numOfSamples, GL_R16F, w, h, GL_TRUE ); 

Configuration de Framebuffer:

  f->glBindFramebuffer(GL_FRAMEBUFFER, framebufferNT); f->glFramebufferTexture2D( GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D_MULTISAMPLE, colorTextureNT, 0 ); f->glFramebufferRenderbuffer( GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, GL_RENDERBUFFER, depthRenderbuffer ); f->glBindFramebuffer(GL_FRAMEBUFFER, framebuffer); f->glFramebufferTexture2D( GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D_MULTISAMPLE, colorTexture, 0 ); f->glFramebufferTexture2D( GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT1, GL_TEXTURE_2D_MULTISAMPLE, alphaTexture, 0 ); GLenum attachments[2] = {GL_COLOR_ATTACHMENT0, GL_COLOR_ATTACHMENT1}; f->glDrawBuffers(2, attachments); f->glFramebufferRenderbuffer( GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, GL_RENDERBUFFER, depthRenderbuffer ); 

Lors de la deuxième passe de rendu, la sortie du fragment shader se fera dans deux textures, qui doivent être explicitement spécifiées avec glDrawBuffers.
La plupart de ce code est exécuté une seule fois, au démarrage du programme. Le code d'allocation de texture et de mémoire tampon est exécuté à chaque fois que la taille de la fenêtre est modifiée. Nous passons maintenant au code exécuté à chaque mise à jour du contenu de la fenêtre.

  f->glBindFramebuffer(GL_FRAMEBUFFER, framebufferNT); // ... rendering non-transparent objects ... // ....... // done! (you didn't expect me to explain how do I render primitives in OpenGL, did you? // It's not relevant for this topic 

Nous venons de rendre tous les objets non transparents dans colorTextureNT et d'écrire les profondeurs dans le rendu du tampon. Avant d'utiliser ce même rendu de mémoire tampon lors de la prochaine passe de rendu, nous devons nous assurer que toutes les opérations d'écriture dans le rendu de mémoire tampon de profondeur à partir d'objets non transparents sont terminées. Il est réalisé avec GL_FRAMEBUFFER_BARRIER_BIT. Une fois les objets transparents rendus, nous allons appeler la fonction ApplyTextures () qui effectuera la passe de rendu finale où le fragment shader échantillonnera à partir des textures colorTextureNT, colorTexture et alphaTexture afin d'appliquer la formule (2). Les textures doivent être prêtes à ce moment, nous utilisons donc GL_TEXTURE_FETCH_BARRIER_BIT avant d'appeler ApplyTextures ().

  static constexpr GLfloat clearColor[4] = { 0.0f, 0.0f, 0.0f, 0.0f }; static constexpr GLfloat clearAlpha = 1.0f; f->glBindFramebuffer(GL_FRAMEBUFFER, framebuffer); f->glClearBufferfv(GL_COLOR, 0, clearColor); f->glClearBufferfv(GL_COLOR, 1, &clearAlpha); f->glMemoryBarrier(GL_FRAMEBUFFER_BARRIER_BIT); PrepareToTransparentRendering(); { // ... rendering transparent objects ... } CleanupAfterTransparentRendering(); f->glMemoryBarrier(GL_TEXTURE_FETCH_BARRIER_BIT); f->glBindFramebuffer(GL_FRAMEBUFFER, defaultFBO); ApplyTextures(); 

defaultFBO est un framebuffer que nous utilisons pour afficher l'image à l'écran. Dans la plupart des cas, c'est 0, mais dans Qt c'est QOpenGLWidget :: defaultFramebufferObject ().

Dans chaque invocation d'un shader de fragment, nous aurons accès à la couleur et à l'opacité du fragment actuel. Mais dans colorTexture doit apparaître une somme (et dans alphaTexture un produit) de ces entités. Pour cela, nous utiliserons le mélange. De plus, étant donné que pour la première texture nous calculons une somme tandis que pour la seconde nous calculons un produit, nous devons fournir différents paramètres de fusion (glBlendFunc et glBlendEquation) pour chaque pièce jointe.

Voici le contenu de la fonction PrepareToTransparentRendering ():

  f->glEnable(GL_DEPTH_TEST); f->glDepthMask(GL_FALSE); f->glDepthFunc(GL_LEQUAL); f->glDisable(GL_CULL_FACE); f->glEnable(GL_MULTISAMPLE); f->glEnable(GL_BLEND); f->glBlendFunci(0, GL_ONE, GL_ONE); f->glBlendEquationi(0, GL_FUNC_ADD); f->glBlendFunci(1, GL_DST_COLOR, GL_ZERO); f->glBlendEquationi(1, GL_FUNC_ADD); 

Et le contenu de la fonction CleanupAfterTransparentRendering ():

  f->glDepthMask(GL_TRUE); f->glDisable(GL_BLEND); 

Dans mon fragment shader, w représente l'opacité. Le produit de la couleur et w - et w lui-même - ira au premier paramètre de sortie, et 1 - w ira au deuxième paramètre de sortie. Un qualificatif de disposition doit être défini pour chaque paramètre de sortie sous la forme de "location = X", où X est un index d'un élément dans le tableau des pièces jointes - celui que nous avons donné à la fonction glDrawBuffers. Pour être précis, le paramètre de sortie avec location = 0 va à la texture liée à GL_COLOR_ATTACHMENT1, et le paramètre avec location = 1 va à la texture liée à GL_COLOR_ATTACHMENT1. Ces mêmes nombres sont utilisés dans les fonctions glBlendFunci et glBlendEquationi pour indiquer la couleur d'attache pour laquelle nous définissons les paramètres de fusion.

Le fragment shader:

 #version 450 core in vec3 color; layout (location = 0) out vec4 outData; layout (location = 1) out float alpha; layout (location = 2) uniform float w; void main() { outData = vec4(w * color, w); alpha = 1 - w; } 

Dans la fonction ApplyTextures (), nous dessinons simplement un rectangle couvrant toute la fenêtre. Le fragment shader échantillonne les données des trois textures en utilisant les coords d'espace d'écran actuels comme coords de texture et un index d'échantillonnage actuel (gl_SampleID) comme index d'échantillonnage pour les textures multi-échantillons. La présence de la variable gl_SampleID dans le code du shader oblige le système à invoquer le fragment shader une fois par échantillon (alors qu'il est normalement invoqué une fois par pixel, en écrivant sa sortie sur tous les échantillons appartenant à une primitive).

Le vertex shader est simple:

 #version 450 core const vec2 p[4] = vec2[4]( vec2(-1, -1), vec2( 1, -1), vec2( 1, 1), vec2(-1, 1) ); void main() { gl_Position = vec4(p[gl_VertexID], 0, 1); } 

Le fragment shader:

 #version 450 core out vec4 outColor; layout (location = 0) uniform sampler2DMS colorTextureNT; layout (location = 1) uniform sampler2DMS colorTexture; layout (location = 2) uniform sampler2DMS alphaTexture; void main() { ivec2 upos = ivec2(gl_FragCoord.xy); vec4 cc = texelFetch(colorTexture, upos, gl_SampleID); vec3 sumOfColors = cc.rgb; float sumOfWeights = cc.a; vec3 colorNT = texelFetch(colorTextureNT, upos, gl_SampleID).rgb; if (sumOfWeights == 0) { outColor = vec4(colorNT, 1.0); return; } float alpha = 1 - texelFetch(alphaTexture, upos, gl_SampleID).r; colorNT = sumOfColors / sumOfWeights * alpha + colorNT * (1 - alpha); outColor = vec4(colorNT, 1.0); } 

Et enfin - Fonction ApplyTextures ():

  f->glActiveTexture(GL_TEXTURE0); f->glBindTexture(GL_TEXTURE_2D_MULTISAMPLE, colorTextureNT); f->glUniform1i(0, 0); f->glActiveTexture(GL_TEXTURE1); f->glBindTexture(GL_TEXTURE_2D_MULTISAMPLE, colorTexture); f->glUniform1i(1, 1); f->glActiveTexture(GL_TEXTURE2); f->glBindTexture(GL_TEXTURE_2D_MULTISAMPLE, alphaTexture); f->glUniform1i(2, 2); f->glEnable(GL_MULTISAMPLE); f->glDisable(GL_DEPTH_TEST); f->glDrawArrays(GL_TRIANGLE_FAN, 0, 4); 

Au final, les ressources OpenGL doivent être libérées. Je le fais dans le destructeur de mon widget OpenGL:

  f->glDeleteFramebuffers (1, &framebufferNT); f->glDeleteTextures (1, &colorTextureNT); f->glDeleteRenderbuffers(1, &depthRenderbuffer); f->glDeleteFramebuffers (1, &framebuffer); f->glDeleteTextures (1, &colorTexture); f->glDeleteTextures (1, &alphaTexture);