Lorsque vous exécutez des requêtes dans
ClickHouse , vous remarquerez peut-être que le profileur affiche souvent la fonction
LZ_decompress_fast vers le haut. Que se passe-t-il? Cette question nous a amenés à nous demander comment choisir le meilleur algorithme de compression.
ClickHouse stocke les données sous forme compressée. Lors de l'exécution de requêtes, ClickHouse essaie d'en faire le moins possible, afin de conserver les ressources CPU. Dans de nombreux cas, tous les calculs potentiellement chronophages sont déjà bien optimisés, et l'utilisateur a écrit une requête bien pensée. Il ne reste alors plus qu'à effectuer la décompression.
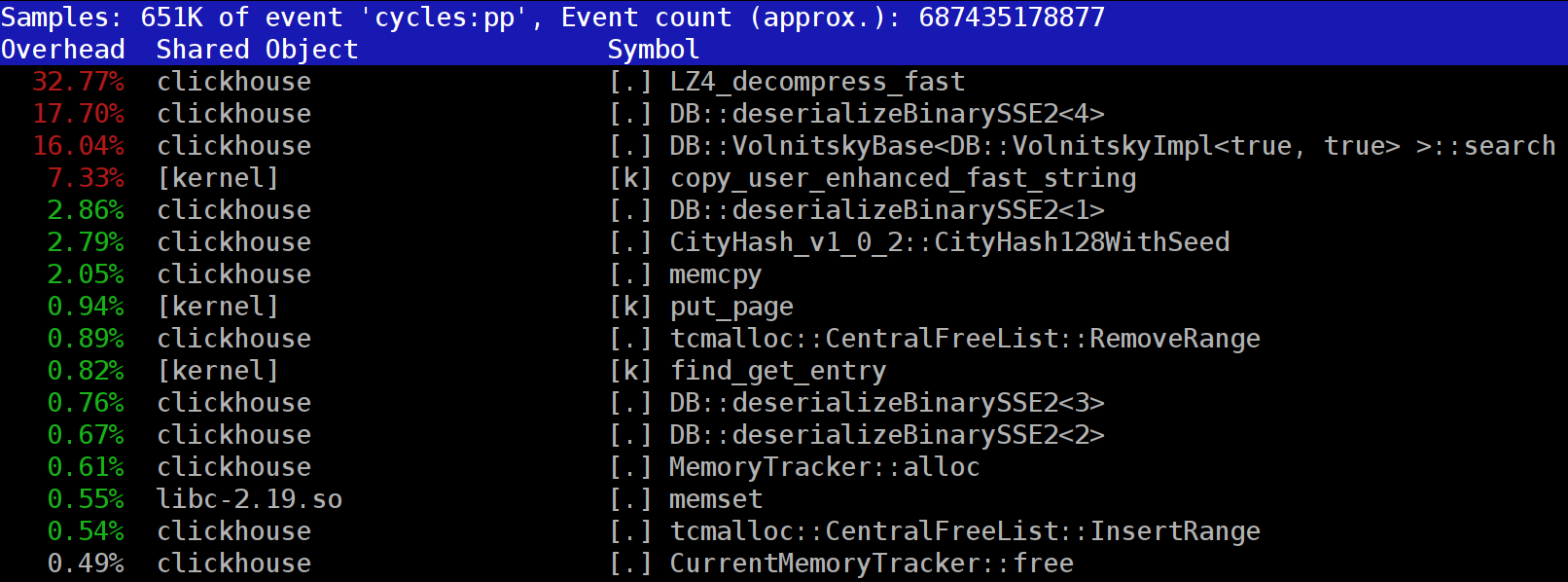
Alors pourquoi la décompression LZ4 devient-elle un goulot d'étranglement? Le LZ4 semble être un
algorithme extrêmement léger : le taux de décompression des données est généralement de 1 à 3 Go / s par cœur de processeur, selon les données. C'est beaucoup plus rapide que le sous-système de disque typique. De plus, nous utilisons tous les cœurs CPU disponibles et les échelles de décompression linéairement sur tous les cœurs physiques.
Cependant, il y a deux points à garder à l'esprit. Tout d'abord, les données compressées sont lues à partir du disque, mais la vitesse de décompression est donnée en termes de quantité de données non compressées. Si le taux de compression est suffisamment élevé, il n'y a presque rien à lire sur les disques. Mais il y aura beaucoup de données décompressées, et cela affecte naturellement l'utilisation du processeur: dans le cas de LZ4, la quantité de travail nécessaire pour décompresser les données est presque proportionnelle au volume des données décompressées elles-mêmes.
Deuxièmement, si les données sont mises en cache, vous n'aurez peut-être pas du tout besoin de lire les données des disques. Vous pouvez compter sur le cache de pages ou utiliser votre propre cache. La mise en cache est plus efficace dans les bases de données orientées colonnes, car seules les colonnes fréquemment utilisées restent dans le cache. C'est pourquoi LZ4 apparaît souvent comme un goulot d'étranglement en termes de charge CPU.
Cela soulève deux autres questions. Premièrement, si la décompression nous ralentit, vaut-il la peine de commencer par compresser les données? Mais cette spéculation n'est pas pertinente dans la pratique. Jusqu'à récemment, la configuration ClickHouse n'offrait que deux options de compression de données - LZ4 et
Zstandard . LZ4 est utilisé par défaut. Le passage à Zstandard rend la compression plus forte et plus lente. Mais il n'y avait pas d'option pour désactiver complètement la compression, car LZ4 est supposé fournir une compression minimale raisonnable qui peut toujours être utilisée. (C'est exactement pourquoi j'aime LZ4.)
Mais un mystérieux inconnu est apparu dans le
chat de support international ClickHouse qui a dit qu'il avait un sous-système de disque très rapide (avec SSD NVMe) et que la décompression était la seule chose qui ralentissait ses requêtes, donc ce serait bien de pouvoir stocker des données sans compression J'ai répondu que nous n'avons pas cette option, mais ce serait facile à ajouter. Quelques jours plus tard, nous avons reçu une
demande d'extraction mettant en œuvre la méthode de compression
none . J'ai demandé au contributeur de rapporter à quel point cette option a aidé à accélérer les requêtes. La réponse a été que cette nouvelle fonctionnalité s'est avérée inutile dans la pratique, car les données non compressées ont commencé à occuper trop d'espace disque et ne cadraient pas avec ces disques NVMe.
La deuxième question qui se pose est que s'il existe un cache, pourquoi ne pas l'utiliser pour stocker des données déjà décompressées? Il s'agit d'une possibilité viable qui éliminera le besoin de décompression dans de nombreux cas. ClickHouse possède également un cache comme celui-ci:
le cache des blocs décompressés . Mais c'est dommage de gaspiller beaucoup de RAM à ce sujet. Il est donc généralement logique de l'utiliser sur de petites requêtes séquentielles qui utilisent des données presque identiques.
Notre conclusion est qu'il est toujours préférable de stocker des données au format compressé. Écrivez toujours les données sur le disque au format compressé. Transmettez également des données sur le réseau avec compression. À mon avis, la compression par défaut est justifiable même lors du transfert de données au sein d'un seul centre de données dans un réseau de 10 Go sans surabonnement, tandis que le transfert de données non compressées entre les centres de données est tout simplement inacceptable.
Pourquoi LZ4?
Pourquoi choisir LZ4? Ne pourrions-nous pas choisir quelque chose d'encore plus léger? Théoriquement, nous pourrions le faire, et c'est une bonne idée. Mais regardons la classe d'algorithmes à laquelle appartient LZ4.
Tout d'abord, il est générique et n'adapte pas le type de données. Par exemple, si vous savez à l'avance que vous disposerez d'un tableau d'entiers, vous pouvez utiliser l'un des algorithmes VarInt et cela utilisera le processeur plus efficacement. Deuxièmement, LZ4 n'est pas trop dépendant des hypothèses du modèle de données. Disons que vous avez une série chronologique ordonnée de valeurs de capteur, un tableau de nombres à virgule flottante. Si vous en tenez compte, vous pouvez calculer des deltas entre ces nombres, puis les compresser avec un algorithme générique, ce qui entraînera un taux de compression plus élevé.
Vous n'aurez aucun problème à utiliser LZ4 avec des tableaux d'octets ou des fichiers. Bien sûr, il a une spécialisation (plus à ce sujet plus tard), et dans certains cas, son utilisation est inutile. Mais si nous l'appelons un algorithme à usage général, nous serons assez proches de la vérité. Notons que grâce à sa conception interne, LZ4 implémente automatiquement l'algorithme
RLE comme cas particulier.
Cependant, la question la plus importante est de savoir si LZ4 est l'algorithme le plus optimal de cette classe en termes de vitesse globale et de force de compression. Les algorithmes optimaux sont appelés la frontière de Pareto, ce qui signifie qu'aucun autre algorithme n'est définitivement meilleur d'une manière et pas pire d'autres (et sur une grande variété de jeux de données également). Certains algorithmes sont plus rapides mais entraînent un taux de compression plus petit, tandis que d'autres ont une compression plus forte mais sont plus lents à compresser ou décompresser.
Pour être honnête, LZ4 n'est pas vraiment la frontière de Pareto - il y a des options disponibles qui sont juste un peu mieux. Par exemple, regardez
LZTURBO d'un développeur surnommé
powturbo . Il n'y a aucun doute sur la fiabilité des résultats, grâce à la communauté
encode.ru (le plus grand et peut-être le seul forum sur la compression de données). Malheureusement, le développeur ne distribue pas le code source ou les binaires; ils ne sont disponibles que pour un nombre limité de personnes pour des tests ou pour beaucoup d'argent (bien qu'il semble que personne ne l'ait encore payé). Jetez également un œil à
Lizard (anciennement LZ5) et à
Densité . Ils peuvent fonctionner légèrement mieux que LZ4 lorsque vous sélectionnez un certain niveau de compression. Une autre option vraiment intéressante est
LZSSE . Mais finissez de lire cet article avant de le consulter.
Comment fonctionne lz4
Voyons comment fonctionne LZ4 en général. C'est l'une des implémentations de l'algorithme LZ77. L et Z représentent les noms des développeurs (Lempel et Ziv), et 77 correspond à l'année 1977 où l'algorithme a été publié. Il a de nombreuses autres implémentations: QuickLZ, FastLZ, BriefLZ, LZF, LZO et gzip et zip si de faibles niveaux de compression sont utilisés.
Un bloc de données compressé à l'aide de LZ4 contient une séquence d'entrées (commandes ou instructions) de deux types:
- Littéraux: "Prenez les N octets suivants tels quels et copiez-les dans le résultat".
- Correspondance: "Prenez N octets du résultat décompressé à partir de la valeur de décalage par rapport à la position actuelle".
Exemple. Avant la compression:
Hello world Hello
Après compression:
literals 12 "Hello world " match 5 12
Si nous prenons un bloc compressé et parcourons le curseur lors de l'exécution de ces commandes, nous obtiendrons les données originales non compressées comme résultat.
Voilà donc essentiellement comment les données sont décompressées. L'idée de base est claire: pour effectuer la compression, l'algorithme code une séquence répétée d'octets à l'aide de correspondances.
Certaines caractéristiques sont également claires. Cet algorithme orienté octets ne dissèque pas les octets individuels; il les copie uniquement dans leur intégralité. C'est ainsi qu'il diffère du codage entropique. Par exemple,
zstd est une combinaison de LZ77 et du codage entropique.
Notez que la taille du bloc compressé ne doit pas être trop grande. La taille est choisie pour éviter de gaspiller beaucoup de RAM pendant la décompression, pour éviter de ralentir trop l'accès aléatoire dans le fichier compressé (qui se compose d'un grand nombre de blocs compressés), et parfois pour que le bloc tienne dans un cache CPU. Par exemple, vous pouvez choisir 64 Ko pour que les tampons pour les données compressées et non compressées tiennent dans le cache L2 avec la moitié encore libre.
Si nous devons compresser un fichier plus volumineux, nous pouvons concaténer les blocs compressés. Cela est également pratique pour stocker des données supplémentaires (comme une somme de contrôle) avec chaque bloc compressé.
Le décalage maximum pour le match est limité. Dans LZ4, la limite est de 64 kilo-octets. Ce montant est appelé la fenêtre coulissante. Cela signifie que les correspondances peuvent être trouvées dans une fenêtre de 64 kilo-octets précédant le curseur, qui glisse avec le curseur à mesure qu'il avance.
Voyons maintenant comment compresser les données ou, en d'autres termes, comment trouver les séquences correspondantes dans un fichier. Vous pouvez toujours utiliser un tri de suffixes (c'est génial si vous en avez déjà entendu parler). Il existe des méthodes qui garantissent que la correspondance la plus longue se trouve dans les octets précédents après la compression. C'est ce qu'on appelle l'analyse optimale et il fournit
presque le meilleur taux de compression pour un bloc compressé au format fixe. Mais il existe de meilleures approches, telles que trouver une correspondance suffisamment bonne qui n'est pas nécessairement la plus longue. Le moyen le plus efficace de le trouver est d'utiliser une table de hachage.
Pour ce faire, nous parcourons le curseur à travers le bloc de données d'origine et prenons quelques octets après le curseur (disons 4 octets). Nous les hachons et mettons l'offset depuis le début du bloc (d'où les 4 octets ont été pris) dans la table de hachage. La valeur 4 est appelée "min-match" - en utilisant cette table de hachage, nous pouvons trouver des correspondances d'au moins 4 octets.
Si nous regardons la table de hachage et qu'elle a déjà un enregistrement correspondant, et que le décalage ne dépasse pas la fenêtre glissante, nous vérifions combien d'octets supplémentaires correspondent après ces 4 octets. Il y a peut-être beaucoup plus de matchs. Il est également possible qu'il y ait une collision dans la table de hachage et que rien ne corresponde, mais ce n'est pas grave. Vous pouvez simplement remplacer la valeur de la table de hachage par une nouvelle. Les collisions dans la table de hachage entraîneront simplement un taux de compression plus faible, car il y aura moins de correspondances. Soit dit en passant, ce type de table de hachage (avec une taille fixe et sans résolution de collisions) est appelé "table de cache". Ce nom est logique car en cas de collision, la table de cache oublie simplement l'ancienne entrée.
Un défi pour le lecteur attentif. Supposons que les données soient un tableau de nombres UInt32 en petit format endian qui représente une partie d'une séquence de nombres naturels: 0, 1, 2 ... Expliquez pourquoi ces données ne sont pas compressées lorsque vous utilisez LZ4 (la taille des données compressées n'est pas plus petit que les données non compressées).
Comment accélérer tout
Je veux donc accélérer la décompression LZ4. Voyons à quoi ressemble la boucle de décompression. Le voici en pseudocode:
while (...) { read(input_pos, literal_length, match_length); copy(output_pos, input_pos, literal_length); output_pos += literal_length; read(input_pos, match_offset); copy(output_pos, output_pos - match_offset, match_length); output_pos += match_length; }
Le format LZ4 est conçu pour que les littéraux et les correspondances alternent dans un fichier compressé. Évidemment, le littéral vient toujours en premier (car il n'y a nulle part où prendre un match au tout début). Par conséquent, leurs longueurs sont codées ensemble.
C'est en fait un peu plus compliqué que ça. Un octet est lu dans le fichier, puis il est divisé en deux quartets (demi-octets) qui contiennent les nombres codés 0 à 15. Si le nombre correspondant n'est pas 15, il est supposé être la longueur du littéral et correspondre, respectivement. Et s'il est de 15, la longueur est plus longue et elle est codée dans les octets suivants. Ensuite, l'octet suivant est lu et sa valeur est ajoutée à la longueur. S'il est égal à 255, la même chose se fait avec l'octet suivant.
Notez que le taux de compression maximum pour le format LZ4 n'atteint pas 255. Et une autre observation inutile est que si vos données sont très redondantes, l'utilisation de LZ4 deux fois améliorera le taux de compression.
Lorsque nous lisons la longueur d'un littéral (puis la longueur de correspondance et le décalage de correspondance), il suffit de copier deux blocs de mémoire pour le décompresser.
Comment copier un bloc de mémoire
Il semblerait que vous pouvez simplement utiliser la fonction
memcpy , qui est conçue pour copier des blocs de mémoire. Mais ce n'est pas l'approche optimale et ce n'est pas vraiment approprié.
L'utilisation de memcpy n'est pas optimale car:
- Il est généralement situé dans la bibliothèque libc (et la bibliothèque libc est généralement liée dynamiquement, donc l'appel memcpy sera effectué indirectement via PLT).
- Il n'est pas inséré par le compilateur si l'argument de taille est inconnu au moment de la compilation.
- Cela demande beaucoup d'efforts pour traiter correctement les restes d'un bloc de mémoire qui ne sont pas des multiples de la longueur ou du registre du mot machine.
Le dernier point est le plus important. Disons que nous avons demandé à la fonction memcpy de copier exactement 5 octets. Ce serait bien de copier 8 octets tout de suite, en utilisant deux instructions movq.
Hello world Hello wo ...
^^^^^ ^^^ - src
^^^^^ ^^^ - dstMais alors nous allons copier trois octets supplémentaires, donc nous allons écrire en dehors des limites du tampon. La fonction
memcpy n'est pas autorisée à le faire, car elle pourrait écraser certaines données de notre programme et entraîner un bogue de mémoire stomping. Et si nous écrivions à une adresse non alignée, ces octets supplémentaires pourraient atterrir sur une page non allouée de mémoire virtuelle ou sur une page sans accès en écriture. Cela nous donnerait un défaut de segmentation (c'est bien).
Mais dans notre cas, nous pouvons presque toujours écrire des octets supplémentaires. Nous pouvons lire des octets supplémentaires dans le tampon d'entrée tant que les octets supplémentaires se trouvent entièrement à l'intérieur. Dans les mêmes conditions, nous pouvons écrire les octets supplémentaires dans le tampon de sortie, car nous les remplacerons toujours à la prochaine itération.
Cette optimisation est déjà dans l'implémentation originale de LZ4:
inline void copy8(UInt8 * dst, const UInt8 * src) { memcpy(dst, src, 8); /// Note that memcpy isn't actually called here. } inline void wildCopy8(UInt8 * dst, const UInt8 * src, UInt8 * dst_end) { do { copy8(dst, src); dst += 8; src += 8; } while (dst < dst_end); }
Pour profiter de cette optimisation, nous devons simplement nous assurer que nous sommes suffisamment éloignés des limites du tampon. Cela ne devrait rien coûter, car nous vérifions déjà le débordement de la mémoire tampon. Et le traitement des derniers octets, les données "restantes", peut être effectué après la boucle principale.
Cependant, il y a encore quelques nuances. La copie se produit deux fois dans la boucle: avec un littéral et une correspondance. Cependant, lors de l'utilisation de la fonction
LZ4_decompress_fast (au lieu de
LZ4_decompress_safe ), la vérification n'est effectuée qu'une seule fois, lorsque nous devons copier le littéral. La vérification n'est pas effectuée lors de la copie de la correspondance, mais la
spécification pour le format LZ4 a des conditions qui vous permettent de l'éviter:
Les 5 derniers octets sont toujours des littéraux.
La dernière correspondance doit commencer au moins 12 octets avant la fin du bloc.
Par conséquent, un bloc de moins de 13 octets ne peut pas être compressé.
Des données d'entrée spécialement sélectionnées peuvent entraîner une corruption de la mémoire. Si vous utilisez la fonction
LZ4_decompress_fast , vous avez besoin d'une protection contre les données incorrectes. À tout le moins, vous devez calculer les sommes de contrôle pour les données compressées. Si vous avez besoin d'une protection contre les pirates, utilisez la fonction
LZ4_decompress_safe . Autres options: prenez une fonction de hachage cryptographique comme somme de contrôle (bien que cela risque de détruire les performances); allouer plus de mémoire aux tampons; allouer de la mémoire pour les tampons avec un appel
mmap séparé et créer une page de garde.
Quand je vois du code qui copie 8 octets de données, je me demande immédiatement pourquoi exactement 8 octets. Vous pouvez copier 16 octets à l'aide des registres SSE:
inline void copy16(UInt8 * dst, const UInt8 * src) { #if __SSE2__ _mm_storeu_si128(reinterpret_cast<__m128i *>(dst), _mm_loadu_si128(reinterpret_cast<const __m128i *>(src))); #else memcpy(dst, src, 16); #endif } inline void wildCopy16(UInt8 * dst, const UInt8 * src, UInt8 * dst_end) { do { copy16(dst, src); dst += 16; src += 16; } while (dst < dst_end); }
La même chose fonctionne pour copier 32 octets pour AVX et 64 octets pour AVX-512. De plus, vous pouvez dérouler la boucle plusieurs fois. Si vous avez déjà vu comment
memcpy , c'est exactement l'approche qui est utilisée. (Soit dit en passant, le compilateur ne déroulera pas ou ne vectorisera pas la boucle dans ce cas, car cela nécessitera l'insertion de contrôles volumineux.)
Pourquoi l'implémentation LZ4 originale n'a-t-elle pas fait cela? Premièrement, il n'est pas clair si c'est mieux ou pire. Le gain résultant dépend de la taille des blocs à copier, donc s'ils sont tous courts, cela créerait du travail supplémentaire pour rien. Et deuxièmement, cela ruine les dispositions au format LZ4 qui permettent d'éviter une branche inutile dans la boucle interne.
Cependant, nous garderons cette option à l'esprit pour le moment.
Copie délicate
Revenons à la question de savoir s'il est toujours possible de copier des données de cette façon. Disons que nous devons copier une correspondance, c'est-à-dire prendre un morceau de mémoire du tampon de sortie situé à un certain décalage derrière le curseur et le copier à la position du curseur.
Imaginez un cas simple lorsque vous devez copier 5 octets avec un décalage de 12:
Hello world ...........
^^^^^ - src
^^^^^ - dst
Hello world Hello wo ...
^^^^^ - src
^^^^^ - dstMais il y a un cas plus difficile, quand nous devons copier un bloc de mémoire plus long que l'offset. En d'autres termes, il inclut des données qui n'ont pas encore été écrites dans le tampon de sortie.
Copiez 10 octets avec un décalage de 3:
abc .............
^^^^^^^^^^ - src
^^^^^^^^^^ - dst
abc abcabcabca ...
^^^^^^^^^^ - src
^^^^^^^^^^ - dstNous avons toutes les données pendant le processus de compression, et une telle correspondance peut très bien être trouvée. La fonction
memcpy ne convient pas pour la copier, car elle ne prend pas en charge le cas où les plages de blocs de mémoire se chevauchent. La fonction
memmove fonctionnera pas non plus, car le bloc de mémoire à partir
memmove les données doivent être extraites n'a pas encore été complètement initialisé. Nous devons copier de la même manière que si nous copions octet par octet.
op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; ...
Voici comment cela fonctionne:
a bc a ............
^ - src
^ - dst
a b ca b ...........
^ - src
^ - dst
ab c ab c ..........
^ - src
^ - dst
abc a bc a .........
^ - src
^ - dst
abca b ca b ........
^ - src
^ - dstEn d'autres termes, nous devons créer une séquence répétitive. L'implémentation originale de LZ4 a utilisé un code étonnamment étrange pour ce faire:
const unsigned dec32table[] = {0, 1, 2, 1, 4, 4, 4, 4}; const int dec64table[] = {0, 0, 0, -1, 0, 1, 2, 3}; const int dec64 = dec64table[offset]; op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; match += dec32table[offset]; memcpy(op+4, match, 4); match -= dec64;
Il copie les 4 premiers octets un par un, avance d'un nombre magique, copie entièrement les 4 octets suivants et déplace le curseur sur une correspondance en utilisant un autre nombre magique. L'auteur du code (
Yan Collet ) a en quelque sorte oublié de laisser un commentaire sur ce que cela signifie. De plus, les noms de variables prêtent à confusion. Ils sont tous les deux nommés dec ... table, mais l'un est ajouté et l'autre est soustrait. De plus, l'un d'eux n'est pas signé et l'autre est int. Cependant, l'auteur a récemment amélioré cette place dans le code.
Voici comment cela fonctionne réellement. Nous copions les 4 premiers octets un à la fois:
abc abca .........
^^^^ - src
^^^^ - dstMaintenant, nous pouvons copier 4 octets à la fois:
abcabca bcab .....
^^^^ - src
^^^^ - dstNous pouvons continuer comme d'habitude, en copiant 8 octets à la fois:
abcabcabcab cabcabca .....
^^^^^^^^ - src
^^^^^^^^ - dstComme nous le savons tous par expérience, la meilleure façon de comprendre le code est parfois de le réécrire. Voici ce que nous avons trouvé:
inline void copyOverlap8(UInt8 * op, const UInt8 *& match, const size_t offset) { /// 4 % n. /// Or if 4 % n is zero, we use n. /// It gives an equivalent result, but is more CPU friendly for unknown reasons. static constexpr int shift1[] = { 0, 1, 2, 1, 4, 4, 4, 4 }; /// 8 % n - 4 % n static constexpr int shift2[] = { 0, 0, 0, 1, 0, -1, -2, -3 }; op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; match += shift1[offset]; memcpy(op + 4, match, 4); match += shift2[offset]; }
Comme prévu, cela ne change pas du tout les performances. Je voulais juste vraiment essayer l'optimisation pour copier 16 octets à la fois.
Cependant, cela complique le "cas spécial" et le fait appeler plus souvent (la condition
offset < 16 est effectuée au moins aussi souvent que
offset < 8 ). La copie des plages qui se chevauchent avec une copie sur 16 octets ressemble à ceci (seul le début est illustré):
inline void copyOverlap16(UInt8 * op, const UInt8 *& match, const size_t offset) { /// 4 % n. static constexpr int shift1[] = { 0, 1, 2, 1, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4 }; /// 8 % n - 4 % n static constexpr int shift2[] = { 0, 0, 0, 1, 0, -1, -2, -3, -4, 4, 4, 4, 4, 4, 4, 4 }; /// 16 % n - 8 % n static constexpr int shift3[] = { 0, 0, 0, -1, 0, -2, 2, 1, 8, -1, -2, -3, -4, -5, -6, -7 }; op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; match += shift1[offset]; memcpy(op + 4, match, 4); match += shift2[offset]; memcpy(op + 8, match, 8); match += shift3[offset]; }
Cette fonction peut-elle être mise en œuvre plus efficacement? Nous aimerions trouver une instruction SIMD magique pour un code aussi complexe, car tout ce que nous voulons faire, c'est écrire 16 octets, qui se composent entièrement de quelques octets de données d'entrée (de 1 à 15). Il suffit ensuite de les répéter dans le bon ordre.
Il y a une instruction comme celle-ci appelée
pshufb (shuffle bytes) qui fait partie de SSSE3 (trois S). Il accepte deux registres de 16 octets. L'un des registres contient les données source. L'autre a le "sélecteur": chaque octet contient un nombre de 0 à 15, en fonction de l'octet du registre source dont il doit extraire le résultat. Si la valeur d'octet du sélecteur est supérieure à 127, l'octet correspondant du résultat est rempli de zéro.
Voici un exemple:
xmm0: abc .............
xmm1: 0120120120120120
pshufb% xmm1,% xmm0
xmm0: abcabcabcabcabca
Chaque octet du résultat est rempli avec l'octet sélectionné des données source - c'est exactement ce dont nous avons besoin! Voici à quoi ressemble le code dans le résultat:
inline void copyOverlap16Shuffle(UInt8 * op, const UInt8 *& match, const size_t offset) { #ifdef __SSSE3__ static constexpr UInt8 __attribute__((__aligned__(16))) masks[] = { 0, 1, 2, 1, 4, 1, 4, 2, 8, 7, 6, 5, 4, 3, 2, 1, /* offset = 0, not used as mask, but for shift amount instead */ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, /* offset = 1 */ 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1, 0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 4, 5, 6, 7, 8, 0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2, 3, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 0, 1, 2, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 0, 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 0, }; _mm_storeu_si128(reinterpret_cast<__m128i *>(op), _mm_shuffle_epi8( _mm_loadu_si128(reinterpret_cast<const __m128i *>(match)), _mm_load_si128(reinterpret_cast<const __m128i *>(masks) + offset))); match += masks[offset]; #else copyOverlap16(op, match, offset); #endif }
Ici,
_mm_shuffle_epi8 est un
intrinsèque , qui se compile avec l'instruction CPU
pshufb .
Pouvons-nous effectuer cette opération pour plusieurs octets à la fois en utilisant des instructions plus récentes? Après tout, SSSE3 est un très ancien jeu d'instructions qui existe depuis 2006. AVX2 a une instruction qui le fait pour 32 octets à la fois, mais séparément pour les voies individuelles de 16 octets. C'est ce qu'on appelle des octets de permutation vectorielle, plutôt que des octets de mélange aléatoire - les mots sont différents, mais la signification est la même. AVX-512 VBMI a une autre instruction qui fonctionne pour 64 octets à la fois, mais les processeurs qui la prennent en charge ne sont apparus que récemment. ARM NEON a des instructions similaires appelées vtbl (recherche de table vectorielle), mais elles ne permettent d'écrire que 8 octets.
De plus, il existe une version de l'instruction
pshufb avec des registres MMX 64 bits pour former 8 octets. C'est parfait pour remplacer la version originale du code. Cependant, j'ai décidé d'utiliser à la place l'option 16 octets (pour des raisons sérieuses).
Lors de la conférence Highload ++ Siberia, un participant est venu vers moi après ma présentation et a mentionné que pour le cas de 8 octets, vous pouvez simplement utiliser la multiplication par une constante spécialement sélectionnée (vous aurez également besoin d'un décalage) - cela ne s'était même pas produit à moi avant!
Comment supprimer une instruction if superflue
Disons que je veux utiliser une variante qui copie 16 octets. Comment puis-je éviter d'avoir à effectuer une vérification supplémentaire pour le dépassement de tampon?
J'ai décidé que je ne ferais pas ce contrôle. Les commentaires sur la fonction diront que le développeur doit allouer un bloc de mémoire pour un nombre spécifié d'octets de plus que nécessaire, afin que nous puissions y lire et écrire des ordures inutiles. L'interface de la fonction sera plus difficile à utiliser, mais c'est un problème différent.
En fait, il pourrait y avoir des conséquences négatives. Disons que les données dont nous avons besoin pour décompresser étaient formées de blocs de 65 536 octets chacun. Ensuite, l'utilisateur nous donne un morceau de mémoire de 65 536 octets pour les données décompressées. Mais avec la nouvelle interface de fonction, l'utilisateur devra par exemple allouer un bloc mémoire de 65 551 octets. L'allocateur peut alors être contraint d'allouer réellement 96 ou même 128 kilo-octets, selon son implémentation. Si l'allocateur est très mauvais, il peut soudainement arrêter la mise en cache de la mémoire dans "heap" et commencer à utiliser
mmap et
munmap chaque fois pour l'allocation de mémoire (ou libérer de la mémoire à l'aide de
madvice ). Ce processus sera extrêmement lent en raison de défauts de page. En conséquence, cette petite optimisation pourrait finir par tout ralentir.
Y a-t-il une accélération?
J'ai donc fait une version du code qui utilise trois optimisations:
- Copie de 16 octets au lieu de 8.
- Utilisation des instructions de lecture aléatoire pour le cas de
offset < 16 . - Suppression d'un extra si.
J'ai commencé à tester ce code sur différents ensembles de données et j'ai obtenu des résultats inattendus.
Exemple 1:
Xeon E2650v2, données du navigateur Yandex, colonne AppVersion.
Référence: 1,67 Go / sec.
16 octets, lecture aléatoire: 2,94 Go / sec (76% plus rapide).
Exemple 2:
Xeon E2650v2, données Yandex Direct, colonne ShowsSumPosition.
Référence: 2,30 Go / sec.
16 octets, lecture aléatoire: 1,91 Go / s (20% plus lent).
J'étais vraiment content au début, quand j'ai vu que tout s'était accéléré à un pourcentage aussi élevé. Ensuite, j'ai vu que rien n'était plus rapide avec les autres fichiers. C'était même un peu plus lent pour certains d'entre eux. J'ai conclu que les résultats dépendent du taux de compression. Plus le fichier est compressé, plus l'avantage de passer à 16 octets est grand. Cela semble naturel: plus le taux de compression est élevé, plus la longueur moyenne des fragments à copier est longue.
Pour enquêter, j'ai utilisé des modèles C ++ pour créer des options de code pour quatre cas: en utilisant des blocs de 8 octets ou 16 octets, et avec ou sans l'instruction shuffle.
template <size_t copy_amount, bool use_shuffle> void NO_INLINE decompressImpl( const char * const source, char * const dest, size_t dest_size)
Des variantes complètement différentes du code fonctionnaient mieux sur différents fichiers, mais lors des tests sur un bureau, la version avec shuffle gagnait toujours. Les tests sur un bureau ne sont pas pratiques car vous devez le faire:
sudo echo 'performance' | tee /sys/devices/system/cpu/cpu*/cpufreq/scaling_governor kill -STOP $(pidof firefox) $(pidof chromium)
Ensuite, je suis allé sur l'un des anciens serveurs de "développement" (avec le processeur Xeon E5645), j'ai pris encore plus de jeux de données et j'ai obtenu presque les résultats opposés, ce qui m'a totalement dérouté. Il s'avère que le choix de l'algorithme optimal dépend du modèle de processeur, en plus du taux de compression. Le processeur détermine quand il est préférable d'utiliser l'instruction de lecture aléatoire, ainsi que le seuil pour savoir quand commencer à utiliser la copie sur 16 octets.
Au fait, lors des tests sur nos serveurs, il est logique de le faire:
sudo kill -STOP $(pidof python) $(pidof perl) $(pgrep -u skynet) $(pidof cqudp-client)
Sinon, les résultats seront instables. Faites également attention à la limitation thermique et au plafonnement de la puissance.
Comment choisir le meilleur algorithme
Nous avons donc quatre variantes de l'algorithme et nous devons choisir la meilleure pour les conditions. Nous pourrions créer un ensemble représentatif de données et de matériel, puis effectuer des tests de charge sérieux et choisir la méthode qui est la meilleure en moyenne. Mais nous n'avons pas de jeu de données représentatif. Pour les tests, j'ai utilisé un échantillon de données de
Yandex Metrica , Yandex Direct, Yandex Browser et des
vols aux États-Unis . Mais cela ne suffit pas, car ClickHouse est utilisé par des centaines d'entreprises à travers le monde. Une optimisation excessive sur un ensemble de données peut entraîner une baisse des performances avec d'autres données et même ne pas le réaliser. Et si les résultats dépendent du modèle de processeur, nous devrons écrire explicitement les conditions dans le code et le tester sur chaque modèle (ou consulter le manuel de référence sur les instructions de timing, qu'en pensez-vous?). Dans les deux cas, cela prend trop de temps.
J'ai donc décidé d'utiliser une autre méthode, ce qui est évident pour les collègues qui ont étudié à notre école d'analyse de données: les
«bandits multi-armés» . Le fait est que la variante de l'algorithme est choisie au hasard, puis nous utilisons des statistiques pour choisir progressivement plus souvent les options qui fonctionnent mieux.
Nous avons de nombreux blocs de données qui doivent être décompressés, nous avons donc besoin d'appels de fonction indépendants pour décompresser les données. Nous pourrions choisir l'un des quatre algorithmes pour chaque bloc et mesurer son temps d'exécution. Une opération comme celle-ci ne coûte généralement rien par rapport au traitement d'un bloc de données, et dans ClickHouse, un bloc de données non compressées fait au moins 64 Ko. (Lisez cet
article sur la mesure du temps.)
Pour mieux comprendre le fonctionnement de l'algorithme des «bandits multi-armés», regardons d'où vient le nom. C'est une analogie avec les machines à sous dans un casino qui ont plusieurs leviers qu'un joueur peut tirer pour obtenir une somme d'argent aléatoire. Le joueur peut tirer les leviers plusieurs fois dans n'importe quel ordre. Chaque levier a une probabilité fixe pour le montant d'argent donné, mais le joueur ne sait pas comment cela fonctionne et ne peut l'apprendre que par l'expérience du jeu. Une fois qu'ils l'ont compris, ils peuvent maximiser leurs gains.
Une approche pour maximiser la récompense consiste à évaluer la distribution de probabilité pour chaque levier à chaque étape sur la base des statistiques de jeu des étapes précédentes. Ensuite, nous «gagnons» mentalement une récompense aléatoire pour chaque levier, en fonction des distributions reçues. Enfin, nous tirons sur le levier qui a eu le meilleur résultat dans notre jeu mental. Cette approche est appelée Thompson Sampling.
Mais nous choisissons un algorithme de décompression. Le résultat est le temps d'exécution en picosecondes par octet: moins il y en a, mieux c'est. Nous considérerons le temps d'exécution comme une variable aléatoire et évaluerons sa distribution à l'aide de statistiques mathématiques. L'approche bayésienne est souvent utilisée pour des tâches comme celle-ci, mais il serait fastidieux d'insérer des formules complexes dans du code C ++. Nous pouvons utiliser une approche paramétrique et dire qu'une variable aléatoire appartient à une famille paramétrique de variables aléatoires, puis évaluer ses paramètres.
Comment sélectionner la famille de variables aléatoires? Par exemple, nous pouvons supposer que le temps d'exécution du code a une distribution normale. Mais c'est absolument faux. Tout d'abord, le temps d'exécution ne peut pas être négatif et la distribution normale prend des valeurs partout sur la droite numérique. Deuxièmement, je suppose que le temps d'exécution aura une "queue" lourde à l'extrémité droite.
Cependant, certains facteurs pourraient faire une bonne idée d'estimer la distribution normale uniquement aux fins de l'échantillonnage de Thompson (malgré le fait que la distribution de la variable cible n'est pas nécessairement normale). La raison en est qu'il est très facile de calculer l'espérance mathématique et la variance, et après un nombre suffisant d'itérations, une distribution normale devient assez étroite, pas très différente des distributions que nous aurions obtenues en utilisant d'autres méthodes. Si nous ne sommes pas trop préoccupés par le taux de convergence lors des premières étapes, ces détails peuvent être ignorés.
This may seem like a somewhat ignorant approach. Experience has shown us that the average time for query execution, website page loading, and so on is "garbage" that isn't worth calculating. It would be better to calculate the median, which is a
robust statistic . But this is a little more difficult, and as I will show later, the described method justifies itself for practical purposes.
At first I implemented calculation of the mathematical expectation and variance, but then I decided that this is too good, and I need to simplify the code to make it "worse":
/// For better convergence, we don't use proper estimate of stddev. /// We want to eventually separate the two algorithms even in cases /// when there is no statistical significant difference between them. double sigma() const { return mean() / sqrt(adjustedCount()); } double sample(pcg64 & rng) const { ... return std::normal_distribution<>(mean(), sigma())(rng); }
I wrote it so that the first few iterations were not taken into account, to eliminate the effect of memory latencies.
The result is a test program that can select the best algorithm for the input data, with optional modes that use the reference implementation of LZ4 or a specific version of the algorithm.
So there are six options:
— Reference (baseline): original LZ4 without our modifications.
— Variant 0: copy 8 bytes at a time without shuffle.
— Variant 1: copy 8 bytes at a time with shuffle.
— Variant 2: copy 16 bytes at a time without shuffle.
— Variant 3: copy 16 bytes at a time with shuffle.
— The "bandit" option, which selects the best of the four optimized variants.
Testing on different CPUs
If the result strongly depends on the CPU model, it would be interesting to find out exactly how it is affected. There might be an exceptionally large difference on certain CPUs.
I prepared a set of datasets from different tables in ClickHouse with real data, for a total of 256 different files each with 100 MB of uncompressed data (the number 256 was coincidental). Then I looked at the CPUs of the servers where I can run benchmarks. I found servers with the following CPUs:
— Intel® Xeon® CPU E5-2650 v2 @ 2.60GHz
— Intel® Xeon® CPU E5-2660 v4 @ 2.00GHz
— Intel® Xeon® CPU E5-2660 0 @ 2.20GHz
— Intel® Xeon® CPU E5645 @ 2.40GHz
— Intel Xeon E312xx (Sandy Bridge)
— AMD Opteron(TM) Processor 6274
— AMD Opteron(tm) Processor 6380
— Intel® Xeon® CPU E5-2683 v4 @ 2.10GHz
— Intel® Xeon® CPU E5530 @ 2.40GHz
— Intel® Xeon® CPU E5440 @ 2.83GHz
— Intel® Xeon® CPU E5-2667 v2 @ 3.30GHz
The most interesting part comes next — the processors provided by the R&D department:
— AMD EPYC 7351 16-Core Processor, a new AMD server processor.
— Cavium ThunderX2, which is AArch64, not x86. For these, my SIMD optimization needed to be reworked a bit. The server has 224 logical and 56 physical cores.
There are 13 servers in total, and each of them runs the test on 256 files in 6 variants (reference, 0, 1, 2, 3, adaptive). The test is run 10 times, alternating between the options in random order. It outputs 199,680 results that we can compare.
For example, we can compare different CPUs with each other. But we shouldn't jump to conclusions from these results, because we are only testing the LZ4 decompression algorithm on a single core (this is a very narrow case, so we only get a micro-benchmark). For example, the Cavium has the lowest performance per single core. But I tested ClickHouse on it myself, and it wins out over Xeon E5-2650 v2 on heavy queries due to the greater number of cores, even though it is missing many optimizations that are made in ClickHouse specifically for the x86.
┌─cpu───────────────────┬──ref─┬─adapt─┬──max─┬─best─┬─adapt_boost─┬─max_boost─┬─adapt_over_max─┐
│ E5-2667 v2 @ 3.30GHz │ 2.81 │ 3.19 │ 3.15 │ 3 │ 1.14 │ 1.12 │ 1.01 │
│ E5-2650 v2 @ 2.60GHz │ 2.5 │ 2.84 │ 2.81 │ 3 │ 1.14 │ 1.12 │ 1.01 │
│ E5-2683 v4 @ 2.10GHz │ 2.26 │ 2.63 │ 2.59 │ 3 │ 1.16 │ 1.15 │ 1.02 │
│ E5-2660 v4 @ 2.00GHz │ 2.15 │ 2.49 │ 2.46 │ 3 │ 1.16 │ 1.14 │ 1.01 │
│ AMD EPYC 7351 │ 2.03 │ 2.44 │ 2.35 │ 3 │ 1.20 │ 1.16 │ 1.04 │
│ E5-2660 0 @ 2.20GHz │ 2.13 │ 2.39 │ 2.37 │ 3 │ 1.12 │ 1.11 │ 1.01 │
│ E312xx (Sandy Bridge) │ 1.97 │ 2.2 │ 2.18 │ 3 │ 1.12 │ 1.11 │ 1.01 │
│ E5530 @ 2.40GHz │ 1.65 │ 1.93 │ 1.94 │ 3 │ 1.17 │ 1.18 │ 0.99 │
│ E5645 @ 2.40GHz │ 1.65 │ 1.92 │ 1.94 │ 3 │ 1.16 │ 1.18 │ 0.99 │
│ AMD Opteron 6380 │ 1.47 │ 1.58 │ 1.56 │ 1 │ 1.07 │ 1.06 │ 1.01 │
│ AMD Opteron 6274 │ 1.15 │ 1.35 │ 1.35 │ 1 │ 1.17 │ 1.17 │ 1 │
│ E5440 @ 2.83GHz │ 1.35 │ 1.33 │ 1.42 │ 1 │ 0.99 │ 1.05 │ 0.94 │
│ Cavium ThunderX2 │ 0.84 │ 0.87 │ 0.87 │ 0 │ 1.04 │ 1.04 │ 1 │
└───────────────────────┴──────┴───────┴──────┴──────┴─────────────┴───────────┴────────────────┘
- ref, adapt, max — The speed in gigabytes per second (the value that is the reverse of the arithmetic mean of time for all launches on all datasets).
- best — The number of the best algorithm among the optimized variants, from 0 to 3.
- adapt_boost — The relative advantage of the adaptive algorithm compared to the baseline.
- max_boost — The relative advantage of the best of the non-adaptive variants compared to the baseline.
- adapt_over_max — The relative advantage of the adaptive algorithm over the best non-adaptive one.
The results show that we were able to speed up decompression by 12-20% on modern x86 processors. Even on ARM we saw 4% improvement, despite the fact that we didn't optimize much for this architecture. It is also clear that on average for different datasets, the "bandit" algorithm comes out ahead of the pre-selected best variant on all processors (except for very old Intel CPUs).
Conclusion
In practice, the usefulness of this work is dubious. Yes, LZ4 decompression was accelerated on average by 12-20%, and on some datasets the performance more than doubled. But in general, this doesn't have much effect on query execution time. It's difficult to find real queries that gain more than a couple percent in speed.
We decided to use ZStandard level 1 instead of LZ4 on several Yandex Metrica clusters intended for executing long queries, because it is more important to save IO and disk space on cold data. Keep this in mind if you have similar workload.
We observed the greatest benefits from optimizing decompression in highly compressible data, such as columns with mostly duplicate string values. However, we have developed a separate solution specifically for this scenario that allows us to significantly speed up queries over this kind of data.
Another point to remember is that optimization of decompression speed is often limited by the format of the compressed data. LZ4 uses a very good format, but Lizard, Density and LZSSE have other formats that can work faster. Perhaps instead of trying to accelerate LZ4, it would be better to just integrate LZSSE into ClickHouse.
It's unlikely that these optimizations will be implemented in the mainstream LZ4 library: in order to use them, the library interface would have to be modified. In fact, this is often the case with improving algorithms — optimizations don't fit into old abstractions and they have to be revised. However, variable names have already been corrected in the original implementation. For instance, inc and dec tables have been
corrected . In addition, about a month ago, the original implementation accelerated decompression by the same 12-15% by copying 32 bytes instead of 16, as discussed above. We tried the 32-byte option ourselves and the results were not that great, but they were still
faster .
If you look at the profile at the beginning of the article, you may notice that we could have removed one extra copying operation from the page cache to userspace (either using
mmap , or using
O_DIRECT and userspace page cache, but both options are problematic). We also could have slightly improved the checksum calculation (CityHash128 is currently used without CRC32-C, but we could use HighwayHash, FARSH or XXH3). Acceleration of these two operations is useful for weakly compressed data, since they are performed on compressed data.
In any case, the changes have already been added to master more than a year ago, and the ideas that resulted from this research have been applied in other tasks. You can also watch the
video from HighLoad++ Siberia, or view the
presentation (both in Russian).