Dans cet article, je partagerai comment j'ai compris l'écriture d'un synthétiseur DDS sur Verilog. Il sera utilisé pour générer une oscillation sinusoïdale, dont la fréquence et la phase initiale peuvent être ajustées et calculées pour être utilisées avec un DAC unipolaire 8 bits. Le fonctionnement du synthétiseur est bien écrit dans un article de la revue Components and Technologies . Pour réduire la quantité de mémoire utilisée de la table sinus, la symétrie est utilisée.
Pour la compilation sous Linux, j'ai utilisé Iverilog et pour l'affichage GTKWave. Pour plus de commodité, un simple Makefile a été écrit, peut-être qu'il sera utile pour quelqu'un. Initialement, en utilisant le compilateur iverilog, nous obtenons le fichier tb.out, puis l'envoyons au simulateur vvp, qui est installé avec iverilog. En conséquence, vvp générera out.vcd, qui contient toutes les variables (signaux) utilisées dans le projet. La cible d'affichage, en plus de ce qui précède, lancera GTKWave avec le fichier variable et vous pouvez voir les formes d'onde des signaux.
SRC = nco.v TB = nco_tb.v all: iverilog -o tb.out $(TB) vvp -lxt tb.out check: iverilog -v $(TB) display: iverilog -o tb.out $(TB) vvp -lxt tb.out gtkwave out.vcd & clean: rm -rf *.out *.vcd *.vvp
Tout d'abord, vous devez placer une table du futur sinus en mémoire, car j'ai écrit un script Python simple qui divise un quart de la période sinusoïdale en 64 points et le génère dans un format qui peut ensuite être copié dans le code source. Depuis que j'ai conçu l'implémentation du DDS pour un DAC unipolaire externe avec une capacité en bits de pas plus de 8 bits, l'amplitude du sinus devrait être comprise entre 0 et 256, où la demi-période négative se situe dans la plage 0 ... 127, et la moitié positive dans 128 ... 255 . À cet égard, les valeurs sinusoïdales obtenues (de 0 à pi / 4) sont multipliées par 127, puis 127 y est ajouté. Par conséquent, les valeurs du premier trimestre de la période sont obtenues, dont l'amplitude est de 128 ... 256.
J'attire l'attention sur le fait qu'avec cette formation, le sinus à la sortie du DAC aura une composante constante. Pour le retirer, il faut le faire passer à travers un condensateur.
import numpy as np x=np.linspace(0,np.pi/2,64) print(np.sin(x)) y=127*np.sin(x) print(len(y)) print(y) z=[] i = 0 for elem in y: if int(elem)<=16: print("lut[%d] = 7'h0%X;" % (i, int(elem))) else: print("lut[%d] = 7'h%X;" % (i, int(elem))) z.append(hex(int(elem))) i = i + 1
Puisque la fonction sinus est symétrique (impair), vous pouvez trouver la première symétrie sin (x) = - sin (pi + x). La deuxième symétrie est caractérisée par le fait que le fait d'avoir une table pour un quart de la période, le deuxième trimestre peut être obtenu en parcourant la table dans l'ordre inverse (puisque le sinus sur la demi-période augmente d'abord, puis diminue).
La majeure partie du synthétiseur DDS est une batterie de phase. Il s'agit essentiellement de l'index d'un élément de la table de recherche (LUT). Pour chaque période du signal d'horloge, la valeur qu'il contient augmente d'une certaine valeur, en conséquence, un sinus est obtenu à la sortie. La fréquence du signal à la sortie dépendra de la valeur de l'incrément de l'accumulateur de phase - plus il est grand, plus la fréquence est élevée. Cependant, selon le critère de Kotelnikov, la fréquence d'échantillonnage devrait être au moins 2 fois la fréquence du signal (pour éviter l'effet de superposition du spectre), d'où la limitation de l'incrément maximum est la moitié de l'accumulateur de phase. En général, le critère d'ingénierie est la fréquence d'échantillonnage = 2,2 de la fréquence du signal, donc, ayant décidé de ne pas aller à l'extrême, j'ai supprimé un bit de plus, en laissant 6 bits incrémentés avec une batterie de phase de 8 bits (même si la jackalite sinusoïdale déjà).
En raison de la symétrie utilisée, seuls les 6 bits inférieurs de 2 ^ 6 = 64 seront directement utilisés pour l'échantillonnage d'index. Les 2 bits supérieurs sont utilisés pour identifier un quart de période de génération de sinus et, en conséquence, changer la direction de la traversée de la table. Vous devriez obtenir quelque chose de similaire à:
module nco(clk, rst, out ); input clk, rst; output reg [7:0] out; reg [5:0] phase_inc = 6'h1; reg [7:0] phase_acc = 0; parameter LUT_SIZE = 64; reg [6:0] lut [0:LUT_SIZE-1]; always @(posedge clk) begin if (rst) begin phase_inc = 6'h1; phase_acc = 0; out = 0; lut[0] = 7'h00; // lut[63] = 7'h7F; end else begin // 1 if (phase_acc[7:6] == 2'b00) begin // LUT out <= {1'b1,lut[phase_acc[5:0]]}; end if (phase_acc[7:6] == 2'b01) begin out <= {1'b1,lut[~phase_acc[5:0]]}; end if (phase_acc[7:6] == 2'b10) begin out <= {1'b0,~lut[phase_acc[5:0]]}; end if (phase_acc[7:6] == 2'b11) begin out <= {1'b0,~lut[~phase_acc[5:0]]}; end phase_acc <= phase_acc + {2'b0,phase_inc}; end end endmodule
Lors de la réinitialisation, nous initialisons tout avec des zéros, à l'exception de la valeur d'incrément de phase, nous la définissons sur un. Pour préserver la synthétisabilité du code, le tableau sera également rempli de valeurs lors de la réinitialisation. Dans un projet réel, il est conseillé d'utiliser la mémoire de bloc intégrée au FPGA à de telles fins et de créer un fichier de configuration distinct pour celui-ci, et d'utiliser le noyau IP dans le projet lui-même.
Une petite explication sur le fonctionnement de la symétrie. A chaque cycle, il est vérifié (sur les 2 bits les plus significatifs) dans quel quart de phase l'accumulateur est actuellement situé. Si le plus élevé = 00, alors la sortie dans le chiffre le plus élevé est 1 (responsable de la demi-onde positive), dans les plus basses - la valeur de la LUT conformément à l'indice. Après que la valeur de l'accumulateur de phase dépasse 63 (le premier trimestre passera), 01 apparaîtra dans les bits hauts et les plus bas seront à nouveau remplis de zéros.
Pour passer la LUT dans l'ordre inverse, il suffit d'inverser les bits les moins significatifs de l'accumulateur de phase (il continuera d'augmenter pour chaque cycle d'horloge, et sa valeur inversée diminuera).
Pour former une demi-onde négative, nous écrivons 0. Dans le bit supérieur de la sortie, nous devons maintenant inverser la valeur elle-même à partir du sinus. Le point ici est que vous devez obtenir une copie miroir du quart du sinus, et si cela n'est pas fait, vous obtenez la même image qu'au premier trimestre, mais abaissée de 127 vers le bas. Vous pouvez le vérifier en supprimant l'inverse dans le code.
On change la fréquence et la phase initiale
Comme déjà décrit ci-dessus, pour changer la fréquence, il faut changer la valeur de l'incrément de phase. De nouvelles entrées apparaîtront:
input [5:0] freq_res; input [7:0] phase;
Pour changer la valeur de l'incrément de phase, il suffit de l'aligner à chaque cycle:
always @(posedge clk) begin if (rst) begin //... end else begin //... phase_inc <= freq_res; end end
Avec la phase initiale, tout n'est pas si simple. Vous devez d'abord l'écrire dans le registre intermédiaire et remplir l'accumulateur de phase avec cette valeur uniquement si la valeur de la phase initiale à l'entrée ne coïncide pas avec celle précédemment enregistrée. Cela soulève un autre point important lié à l'état des races. Nous avons déjà un endroit où nous écrivons phase_acc dans le registre. Vous ne pouvez pas enregistrer en même temps à plusieurs endroits, car les données arrivées en premier seront enregistrées. Par conséquent, la conception ressemblera à ceci:
reg change_phase = 0; // // ( ) // : prev_phase <= phase; if (phase != prev_phase) begin // change_phase <= 1'b1; end if (change_phase) begin // phase_acc <= prev_phase; change_phase <= 1'b0; end else begin // phase_acc <= phase_acc + {2'b0,phase_inc}; end
Banc d'essai
Le code du banc d'essai pour Iverilog et GTKWave a certains modèles (avec un signe dollar) qui ne sont pas utilisés dans l'ISE Design Suite ou Quartus habituel. Leur signification se résume à sélectionner des signaux surveillés et à les charger dans un fichier, afin qu'ils puissent ensuite être transférés vers le simulateur. Le travail du banc d'essai lui-même est trivial - nous effectuons une réinitialisation, définissons la fréquence / phase initiale et attendons un peu.
`include "nco.v" `timescale 1ns / 1ps module nco_tb; reg clk = 0, rst = 0; reg [7:0] phase = 0; reg [5:0] freq_res; wire [7:0] out; nco nco_inst ( .clk(clk), .rst(rst), .phase(phase), .freq_res(freq_res), .out(out) ); always #2 clk <= ~clk; initial begin $dumpfile("out.vcd"); $dumpvars(0, nco_tb); //$monitor("time =%4d out=%h",$time,out); rst = 1'b1; freq_res = 1; #8 rst = 1'b0; #300 phase = 8'b00100011; #300 phase = 8'b00001111; #1200 freq_res = 6'b111101; #1200 freq_res = 6'b001111; #1200 freq_res = 6'b011111; #400 phase = 8'b00010011; #1200 $finish; end endmodule
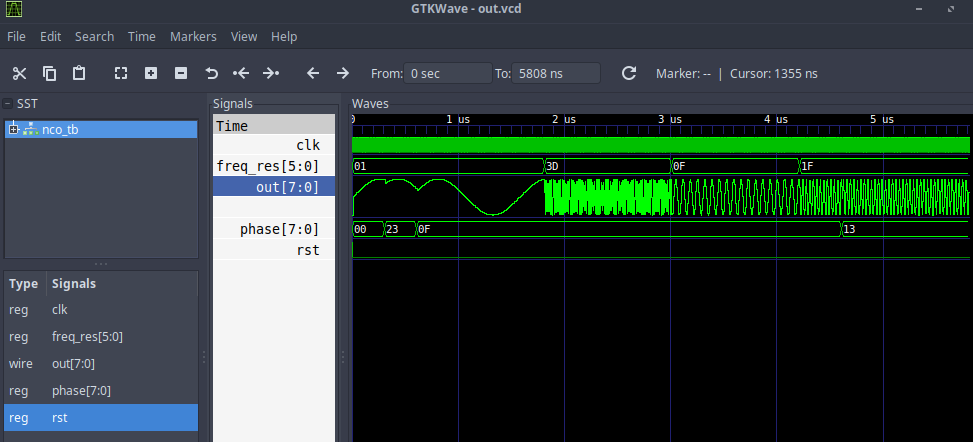
Chronogrammes
En sortie, nous obtenons quelque chose de similaire à un sinus avec une fréquence et une phase initiale changeantes aux moments définis dans le banc de test. Il convient de noter qu'avec l'augmentation de la fréquence, la résolution le long de celle-ci (le nombre d'échantillons par période) diminue, respectivement, la fréquence d'horloge du synthétiseur et sa taille LUT jouent un rôle décisif dans la reproduction du sinus pur (plus sa forme s'approche de l'idéal, moins il y a de composants latéraux dans le spectre du résultat obtenu). signal et le pic sera déjà à la fréquence générée).

On peut voir qu'un signal avec une deuxième fréquence n'a déjà pas un sinus aussi lisse que les autres. Examinons de plus près.

On peut voir que c'est toujours un peu similaire au sinus, le résultat deviendra encore meilleur après qu'un tel signal soit passé à travers un filtre anti-aliasing (filtre passe-bas).
Les sources du projet sont disponibles ici .
Les sources