La propriété de symétrie de la relation de cointégration

Le but de cet article est de partager des résultats paradoxaux dans l'étude de la co-intégration des séries temporelles : si les séries temporelles $$$A$ co-intégré avec à proximité $$$B$ ligne $$$B$ pas toujours co-intégré avec un certain nombre $$$A$ .

Si nous étudions la cointégration de manière purement théorique, il est facile de prouver que si la série $$$A$ co-intégré avec $$$B$ puis ramer $$$B$ co-intégré avec $$$A$ . Cependant, si nous commençons à étudier empiriquement la cointégration, il s'avère que les calculs théoriques ne sont pas toujours confirmés. Pourquoi cela se produit-il?

Symétrie

Attitude $$$A$ appelé symétrique si $$$A \ subseteq A ^ {- 1}$ où $$$A ^ {- 1}$ - le rapport inverse défini par la condition: $$$x A ^ {- 1} y$ équivaut à $$$yAx$ . En d'autres termes, si la relation $$$xAy$ alors la relation $$$yAx$ .

Considérez deux $$$I (1)$ un certain nombre de $$$x_t$ et $$$y_t$ , $$$t = 0, \ points, T$ . La cointégration est symétrique si $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ implique $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ c'est-à-dire si la présence d'une régression directe conduit à la présence de l'inverse.

Considérez l'équation $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ , $$$\ beta_1 \ neq 0$ . Échangez les côtés gauche et droit et soustrayez $$$\ varepsilon_ {1t}$ des deux parties: $$$\ beta_1 x_t = y_t - \ varepsilon_ {1t}$ . Depuis $$$\ beta_1 \ neq 0$ par définition, divisez les deux parties en $$$\ beta_1$ :

$$

$$x_t = \ frac {1} {\ beta_1} y_t - \ frac {\ varepsilon_ {1t}} {\ beta_1}.$$

Remplacer $$$1 / \ beta_1$ sur $$$\ beta_2$ et $$$- \ varepsilon_ {1t} / \ beta_1$ sur $$$\ varepsilon_ {2t}$ nous obtenons $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ . Par conséquent, la relation de cointégration est symétrique.

Il s'ensuit que si la variable $$$X$ cointégré avec variable $$$Y$ puis la variable $$$Y$ doit être co-intégré avec la variable $$$X$ . Cependant, le test de cointégration Angle-Granger ne confirme pas toujours cette propriété de symétrie, car parfois une variable $$$Y$ pas co-intégré avec variable $$$X$ selon ce test.

J'ai testé la propriété de symétrie sur les données 2017 des échanges de Moscou et New York en utilisant le test Angle-Granger. Il y avait 7 975 paires d'actions co-intégrées à la Bourse de Moscou. Pour 7731 (97%) paires cointégrées, la propriété de symétrie a été confirmée, pour 244 (3%) paires cointégrées, la propriété de symétrie n'a pas été confirmée.

Il y avait 140 903 paires d'actions co-intégrées à la Bourse de New York. Pour 136586 (97%) paires cointégrées, la propriété de symétrie a été confirmée, pour 4317 (3%) paires cointégrées, la propriété de symétrie n'a pas été confirmée.

Interprétation

Ce résultat peut être interprété par la faible puissance et la forte probabilité d'erreur du deuxième type de test Dickey-Fuller, sur lequel le test Angle-Granger est basé. La probabilité d'une erreur du deuxième type peut être notée par $$$\ beta = P (H_0 | H_1)$ puis la valeur $$$1 - \ beta$ appelé la puissance du test. Malheureusement, le test de Dickey-Fuller n'est pas en mesure de faire la distinction entre les séries chronologiques non stationnaires et quasi-non stationnaires.

Qu'est-ce qu'une série chronologique quasi instable? Considérez la série chronologique $$$x_t = \ phi x_ {t-1} + \ varepsilon_t$ . Une série chronologique stationnaire est une série dans laquelle $$$0 <\ phi <1$ . Une série chronologique non stationnaire est une série dans laquelle $$$\ phi = 1$ . Une série chronologique quasi instable est une série dans laquelle la valeur $$$\ phi$ près d'un.

Dans le cas de séries chronologiques quasi-non stationnaires, nous ne sommes souvent pas en mesure de rejeter l'hypothèse nulle de non stationnaire. Cela signifie que le test de Dickey-Fuller présente un risque élevé d'erreur de deuxième type, c'est-à-dire la probabilité de ne pas rejeter l'hypothèse de faux nul.

Test KPSS

Une réponse possible à la faiblesse du test Dickey-Fuller est le test KPSS, qui doit son nom aux initiales des scientifiques de Kvyatkovsky, Phillips, Schmidt et Sheen. Bien que l'approche méthodologique de ce test soit complètement différente de l'approche de Dickey-Fuller, la principale différence doit être comprise dans la permutation des hypothèses nulles et alternatives.

Dans le test KPSS, l'hypothèse nulle indique que la série chronologique est stationnaire, par rapport à l'alternative concernant la présence de non-stationnarité. Les séries chronologiques quasi non stationnaires, qui ont souvent été identifiées comme non stationnaires à l'aide du test Dickey-Fuller, peuvent être correctement identifiées comme stationnaires à l'aide du test KPSS.

Cependant, nous devons être conscients que les résultats des tests statistiques ne sont que probabilistes et ne doivent pas être confondus avec un certain vrai jugement. Il y a toujours une probabilité non nulle que nous nous trompions. Pour cette raison, il est proposé de combiner les résultats des tests Dickey-Fuller et KPSS comme test idéal pour la non-stationnarité.



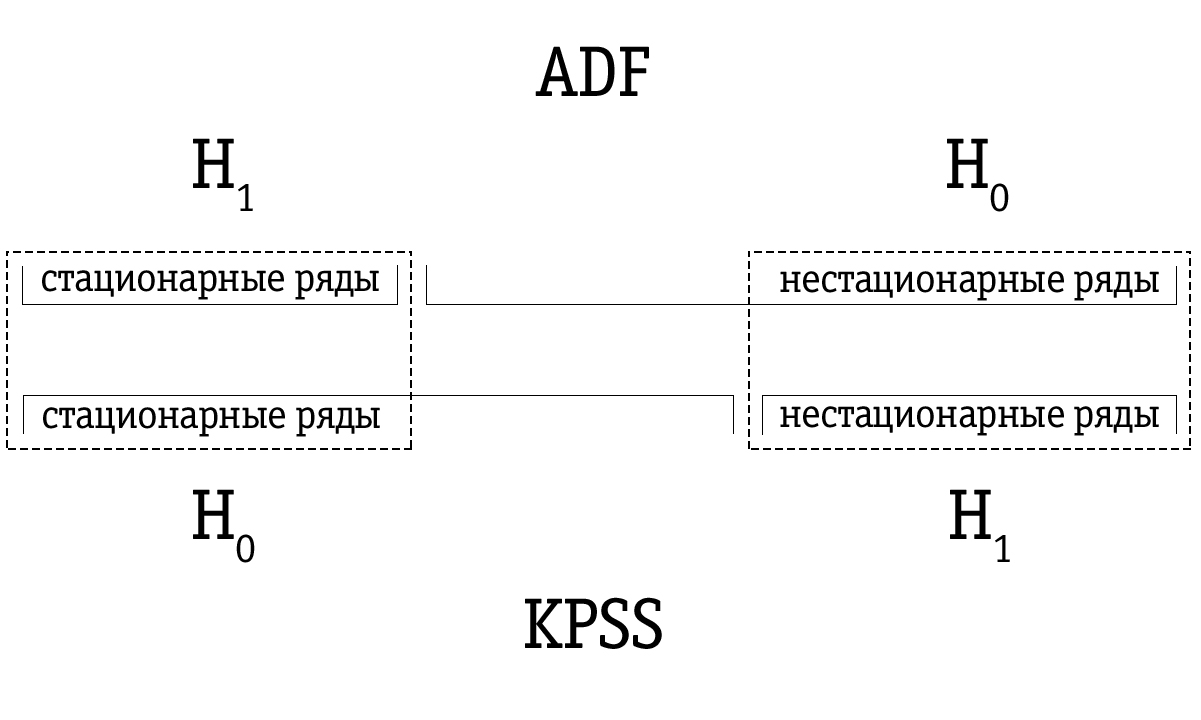
En raison de la faible puissance, le test Dickey-Fuller identifie souvent à tort une série comme non stationnaire, de sorte que l'ensemble de séries temporelles résultant identifié par le test Dickey-Fuller comme instable s'avère être plus grand par rapport à de nombreuses séries temporelles identifiées comme non stationnaires à l'aide du test KPSS. Par conséquent, l'ordre de test est important.

Si la série chronologique est identifiée comme stationnaire à l'aide du test de Dickey-Fuller, elle sera très probablement également identifiée comme stationnaire à l'aide du test KPSS; dans ce cas, on peut supposer que la série est bien stationnaire.

Si la série chronologique a été identifiée comme instable à l'aide du test KPSS, elle sera très probablement identifiée comme instable à l'aide du test Dickey-Fuller; dans ce cas, nous pouvons supposer que la série est en effet instable.

Cependant, il arrive souvent qu'une série chronologique identifiée comme non stationnaire à l'aide du test Dickey-Fuller soit marquée comme stationnaire à l'aide du test KPSS. Dans ce cas, nous devons être très prudents avec notre conclusion finale. Nous pouvons vérifier la solidité de la base de la stationnarité dans le cas du test KPSS et de l'instabilité dans le cas du test Dickey-Fuller et prendre une décision appropriée. Bien sûr, nous pouvons également laisser la question de la stationnarité d'une telle série chronologique non résolue.

L'approche de test KPSS suppose des séries chronologiques $$$y_t$ la stationnarité testée par rapport à une tendance peut être décomposée en la somme d'une tendance déterministe $$$\ beta t$ marche aléatoire $$$r_t$ et erreur stationnaire $$$\ varepsilon_t$ :

$$

$$y_t = \ beta t + r_t + \ varepsilon_t, \\ r_t = r_ {t-1} + u_t,$$

où $$$u_t$ - processus iid normal avec moyenne et variance nulles $$$\ sigma ^ 2$ ( $$$u_t \ sim N (0, \ sigma ^ 2)$ ) Valeur initiale $$$r_0$ traité comme fixe et joue le rôle d'un membre libre. Erreur stationnaire $$$\ varepsilon_t$ peut être généré par n'importe quel processus ARMA commun, c'est-à-dire qu'il peut avoir une forte autocorrélation.

Semblable au test de Dickey-Fuller, la capacité de prendre en compte une structure arbitraire d'autocorrélation $$$\ varepsilon_t$ très important car la plupart des séries chronologiques économiques dépendent fortement du temps et ont donc une forte autocorrélation. Si nous voulons vérifier la stationnarité par rapport à l'axe horizontal, alors le terme $$$\ beta t$ juste exclus de l'équation ci-dessus.

De l'équation ci-dessus, il résulte que l'hypothèse nulle $$$H_0$ sur la stationnarité $$$y_t$ équivalent à l'hypothèse $$$\ sigma ^ 2 = 0$ , dont il résulte que $$$r_t = r_0$ pour tous $$$t$ ( $$$r_0$ Est une constante). De même, une hypothèse alternative $$$H_1$ la non-stationnarité est équivalente à l'hypothèse $$$\ sigma ^ 2 \ neq 0$ .

Pour tester l'hypothèse $$$H_0$ : $$$\ sigma ^ 2 = 0$ (séries chronologiques stationnaires) versus alternative $$$H_1$ : $$$\ sigma ^ 2 \ neq 0$ (séries chronologiques non stationnaires) les auteurs du test KPSS reçoivent des statistiques à sens unique du test du multiplicateur de Lagrange. Ils calculent également sa distribution asymptotique et modélisent les valeurs critiques asymptotiques. Nous ne considérons pas ici les détails théoriques, mais ne décrivons que brièvement l'algorithme d'exécution des tests.

Lors de l'exécution du test KPSS pour une série chronologique $$$y_t$ , $$$t = 1, \ points, T$ la méthode des moindres carrés (moindres carrés) est utilisée pour estimer l'une des équations suivantes:

$$

$$y_t = a_0 + \ varepsilon_t, \\ y_t = a_0 + \ beta t + \ varepsilon_t.$$

Si nous voulons vérifier la stationnarité par rapport à l'axe horizontal, nous évaluons la première équation. Si nous prévoyons de vérifier la stationnarité par rapport à la tendance, nous choisissons la deuxième équation.

Restes $$$e_t$ à partir de l'équation estimée sont utilisés pour calculer les statistiques du test des multiplicateurs de Lagrange. Le test du multiplicateur de Lagrange est basé sur l'idée que lorsque l'hypothèse nulle est remplie, tous les multiplicateurs de Lagrange doivent être égaux à zéro.

Test du multiplicateur de Lagrange

Le test du multiplicateur de Lagrange est associé à une approche plus générale de l'estimation des paramètres utilisant la méthode du maximum de vraisemblance (ML). Selon cette approche, les données sont considérées comme des preuves liées aux paramètres de distribution. Les preuves sont exprimées en fonction de paramètres inconnus - une fonction de vraisemblance:

$$

$$L (X_1, X_2, X_3, \ dots, X_n; \ Phi_1, \ Phi_2, \ dots, \ Phi_k),$$

où $$$X_i$ Les valeurs observées sont-elles, et $$$\ Phi_i$ - les paramètres que nous voulons évaluer.

La fonction de vraisemblance maximale est la probabilité conjointe d'observations d'échantillons.

$$

$$L (X_1, X_2, X_3, \ dots, X_n; \ Phi_1, \ Phi_2, \ dots, \ Phi_k) = P (X_1 \ land X_2 \ land X_3 \ dots X_n).$$

Le but de la méthode du maximum de vraisemblance est de maximiser la fonction de vraisemblance. Ceci est réalisé en différenciant la fonction de probabilité maximale pour chacun des paramètres estimés et en égalisant les dérivées partielles à zéro. Les valeurs des paramètres pour lesquels la valeur de la fonction est maximale est l'estimation souhaitée.

Habituellement, pour simplifier le travail ultérieur, le logarithme de la fonction de vraisemblance est d'abord pris.

Considérons un modèle linéaire généralisé $$$Y = \ beta X + \ varepsilon$ où il est supposé que $$$\ varepsilon$ normalement distribué $$$N (0, \ sigma ^ 2)$ c'est $$$Y - \ beta X \ sim N (0, \ sigma ^ 2)$ .

Nous voulons tester l'hypothèse que le système $$$q$ ( $$$q <k$ ) contraintes linéaires indépendantes $$$R \ beta = r$ . Ici $$$R$ - célèbre $$$q \ fois k$ matrice de classement $$$q$ et $$$r$ - célèbre $$$q \ fois 1$ vecteur.

Pour chaque paire de valeurs observées $$$X$ et $$$Y$ dans des conditions normales, une fonction de densité de probabilité de la forme suivante existera:

$$

$$f (X_i, Y_i) = \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} \ left (\ frac {Y_i - \ beta X_i} {\ sigma} \ droite) ^ 2}.$$

Sous réserve de $$$n$ observations conjointes $$$X$ et $$$Y$ la probabilité totale d'observer toutes les valeurs de l'échantillon est égale au produit des valeurs individuelles de la fonction de densité de probabilité. Ainsi, la fonction de vraisemblance est définie comme suit:

$$

$$L (\ beta) = \ prod \ limits_ {i = 1} ^ n \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} \ left (\ frac {Y_i - \ beta X_i} {\ sigma} \ droite) ^ 2}.$$

Puisqu'il est plus facile de différencier la somme que le produit, le logarithme de la fonction de vraisemblance est généralement pris, ainsi:

$$

$$\ ln L (\ beta) = \ sum \ limits_ {i = 1} ^ n \ left (\ ln \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} - \ frac {1} { 2 \ sigma ^ 2} (Y_i - \ beta X_i) ^ 2 \ à droite).$$

Cette conversion utile n'affecte pas le résultat final, car $$$\ ln L$ Est une fonction croissante $$$L$ . Alors la valeur $$$\ beta$ qui maximise $$$\ ln L$ maximisera également $$$L$ .

Score ML pour $$$\ beta$ en régression avec restriction ( $$$R \ beta = r$ ) est obtenu en maximisant la fonction $$$\ ln L (\ beta)$ sous réserve de $$$R \ beta = r$ . Pour trouver cette estimation, nous écrivons la fonction de Lagrange:

$$

$$\ psi (\ beta) = \ ln L (\ beta) - g '(R \ beta - r),$$

par où $$$g = \ left (g_1, \ dots, g_q \ right) '$ vecteur marqué $$$q$ Multiplicateurs de Lagrange.

Statistiques de test du multiplicateur de Lagrange indiquées par $$$\ eta_ \ mu$ en cas de stationnarité par rapport à l'axe horizontal et traversant $$$\ eta_ \ tau$ en cas de stationnarité par rapport à la tendance, elle est déterminée par l'expression

$$

$$\ eta _ {\ mu / \ tau} = T ^ 2 \ frac {1} {s ^ 2 (l)} \ sum \ limits_ {t = 1} ^ T S_t ^ 2,$$

où

$$

$$S_t = \ sum \ limits_ {i = 1} ^ t e_i$$

et

$$

$$s ^ 2 (l) = T ^ {- 1} \ sum \ limits_ {t = 1} ^ T e_t ^ 2 + 2 T ^ {- 1} \ sum \ limits_ {1} ^ lw (s, l) \ sum \ limits_ {t = s + 1} ^ T e_t e_ {ts},$$

où

$$

$$w (s, l) = 1 - \ frac {s} {l + 1}.$$

Dans les équations ci-dessus $$$S_t$ - le processus des soldes partiels $$$e_t$ à partir de l'équation estimée; $$$s ^ 2 (l)$ - évaluation de la dispersion à long terme des résidus $$$e_t$ ; mais $$$w (s, l)$ - la fenêtre spectrale dite de Bartlett, où $$$l$ - paramètre de troncature de décalage.

Dans cette application, la fenêtre spectrale est utilisée pour estimer la densité spectrale des erreurs pour un certain intervalle (fenêtre), qui se déplace sur toute la plage de la série. Les données en dehors de l'intervalle sont ignorées, car la fonction fenêtre est une fonction égale à zéro en dehors d'un intervalle sélectionné (fenêtre).

Estimation de la variance $$$s ^ 2 (l)$ dépend du paramètre $$$l$ , et depuis $$$l$ augmente et plus de 0, marque $$$s ^ 2 (l)$ commence à prendre en compte une éventuelle autocorrélation dans les résidus $$$e_t$ .

Enfin, les statistiques du test du multiplicateur de Lagrange $$$\ eta_ \ mu$ ou $$$\ eta_ \ tau$ se compare aux valeurs critiques. Si les statistiques du test du multiplicateur de Lagrange dépassent la valeur critique correspondante, alors l'hypothèse nulle $$$H_0$ (séries chronologiques stationnaires) s'écarte en faveur d'une hypothèse alternative $$$H_1$ (séries chronologiques non stationnaires). Sinon, on ne peut pas rejeter l'hypothèse nulle $$$H_0$ sur la stationnarité d'une série chronologique.

Les valeurs critiques sont asymptotiques et conviennent donc le mieux aux grands échantillons. Cependant, en pratique, ils sont également utilisés pour un petit échantillon. De plus, les valeurs critiques sont indépendantes du paramètre $$$l$ . Cependant, les statistiques du test du multiplicateur de Lagrange dépendront du paramètre $$$l$ . Les auteurs du test KPSS ne proposent aucun algorithme général pour choisir le paramètre approprié. $$$l$ . Le test est généralement effectué pour $$$l$ dans la plage de 0 à 8.

Avec augmentation $$$l$ nous sommes moins susceptibles de rejeter l'hypothèse nulle $$$H_0$ sur la stationnarité, ce qui conduit partiellement à une diminution de la puissance du test et peut donner des résultats mitigés. Cependant, en général, nous pouvons dire que si l'hypothèse nulle $$$H_0$ la stationnarité de la série temporelle n'est pas rejetée même à de petites valeurs $$$l$ (0, 1 ou 2), nous concluons que les séries chronologiques vérifiées sont stationnaires.

Comparaison des résultats des tests

La méthodologie suivante a été développée pour évaluer la probabilité de symétrie.

1. Toutes les séries chronologiques sont vérifiées pour l'intégrabilité du premier ordre en utilisant le test de Dickey-Fuller à un niveau de signification de 0,05. Seules les séries intégrables du premier ordre sont considérées ci-dessous.
2. Les séries intégrables de premier ordre obtenues dans la section 1 comprennent des paires en combinant sans répétition.
3. Les paires d'actions établies à l'article 2 sont testées pour la cointégration en utilisant le test Angle-Granger. En conséquence, des paires cointégrées sont identifiées.
4. Les résidus de régression obtenus à la suite des tests du paragraphe 3 sont testés pour la stationnarité en utilisant le test KPSS. Ainsi, les résultats des deux tests sont combinés.
5. Les séries chronologiques dans les paires cointégrées de la section 2 sont échangées et vérifiées à nouveau pour la cointégration en utilisant le test Angle-Granger, c'est-à-dire que nous examinons si la relation entre les séries chronologiques est symétrique.
6. Les séries chronologiques dans les paires co-intégrées de l'élément 4 sont échangées et les résidus de la régression sont à nouveau vérifiés pour la stationnarité en utilisant le test KPSS, c'est-à-dire que nous examinerons si la relation entre les séries chronologiques est symétrique.

Tous les calculs sont effectués à l'aide du package MATLAB. Les résultats sont présentés dans le tableau ci-dessous. Pour chaque test, nous avons un certain nombre de relations symétriques selon les résultats du test (marquées $$$S$ ); nous avons un certain nombre de relations qui ne sont pas symétriques selon les résultats des tests (marqués $$$¬S$ ); et nous avons une probabilité empirique que le rapport soit symétrique selon les résultats des tests ( $$$P (S) = \ frac {S} {S + ¬S}$ )

Sur la Bourse de Moscou:


À la Bourse de New York:

Comparaison des résultats des backtests

Comparons les résultats d'une stratégie de trading sur des données historiques pour les paires co-intégrées sélectionnées à l'aide du test Angle-Granger et pour les paires co-intégrées sélectionnées à l'aide du test KPSS.

Comme le montre le tableau, en raison d'une identification plus précise des paires d'actions co-intégrées, il a été possible d'augmenter le rendement annuel moyen lors de la négociation d'une paire co-intégrée séparée de 9,21%. Ainsi, la méthodologie proposée peut augmenter la rentabilité du trading algorithmique en utilisant des stratégies neutres sur le marché.

Interprétation alternative

Comme nous l'avons vu ci-dessus, les résultats du test Angle-Granger sont une loterie. Pour certains, mes pensées sembleront trop catégoriques, mais je pense qu'il est très logique de ne pas prendre l'hypothèse nulle, confirmée par l'analyse statistique, sur la foi.

Le conservatisme de la méthode scientifique pour tester les hypothèses est que lors de l'analyse des données, nous ne pouvons faire qu'une seule conclusion valide: l'hypothèse nulle est rejetée au niveau de signification choisi. Cela ne signifie pas que l'alternative est vraie. $$$H_1$ - nous venons de recevoir une preuve indirecte de sa crédibilité sur la base d'une "preuve du contraire" typique. Dans le cas où c'est vrai $$$H_0$ , le chercheur est également chargé de tirer une conclusion prudente: sur la base des données obtenues dans les conditions expérimentales, il n'a pas été possible de trouver suffisamment de preuves pour rejeter l'hypothèse nulle.

À l'unisson de mes réflexions de septembre 2018, un article a été écrit par des personnes influentes appelant à abandonner le concept de «signification statistique» et le paradigme du test de l'hypothèse nulle.

Plus important encore: «Des suggestions telles que la modification du niveau de seuil $$$p$ -les valeurs par défaut, l'utilisation d'intervalles de confiance en mettant l'accent sur le fait qu'ils contiennent zéro ou non, ou l'utilisation du coefficient de Bayes avec des classifications universellement acceptées pour évaluer la force des preuves provenant de problèmes identiques ou similaires à l'utilisation actuelle $$$p$ -les valeurs avec un niveau de 0,05 ... sont une forme d'alchimie statistique qui fait une fausse promesse de transformer le hasard en fiabilité, le soi-disant «blanchiment de l'incertitude» (Gelman, 2016), qui commence par des données et se termine par des conclusions dichotomiques sur la vérité ou la fausseté - déclarations binaires "il y a un effet" ou "aucun effet" - sur la base de la réalisation de certains $$$p$ -valeurs ou autre valeur seuil.

(Carlin, 2016; Gelman, 2016), , ( ) , , .»

Conclusions

Nous avons vu que bien que la propriété de symétrie de la relation de cointégration soit théoriquement satisfaite, les données expérimentales divergent des calculs théoriques. L'une des interprétations de ce paradoxe est la faible puissance du test de Dickey-Fuller.

En tant que nouvelle méthodologie pour identifier les paires d'actifs co-intégrées, il a été proposé de tester les résidus de régression obtenus en utilisant le test Angle-Granger pour la stationnarité en utilisant le test KPSS et de combiner les résultats de ces tests; et combiner les résultats du test Angle-Granger et du test KPSS pour la régression directe et inverse.

Des backtests ont été effectués sur les données de la Bourse de Moscou pour 2017. Selon les résultats des backtests, le rendement annuel moyen lors de l'utilisation de la méthodologie d'identification des paires d'actions cointégrées proposé ci-dessus était de 22,72%. Ainsi, par rapport à l'identification de paires de stocks co-intégrées à l'aide du test Angle-Granger, il a été possible d'augmenter le rendement annuel moyen de 9,21%.

Une autre interprétation du paradoxe est de ne pas prendre l'hypothèse nulle, confirmée par l'analyse statistique, sur la foi. Le paradigme de test d'hypothèse nulle et la dichotomie offerte par un tel paradigme nous donnent un faux sens de la connaissance du marché.

Quand je viens de commencer mes recherches, il me semblait que vous pouvez prendre le marché, le mettre dans le "hachoir à viande" des tests statistiques et obtenir des rangées savoureuses filtrées à la sortie. Malheureusement, je vois maintenant que ce concept de force brute statistique ne fonctionnera pas.

Qu'il y ait ou non cointégration sur le marché - pour moi, cette question reste ouverte. J'ai encore de grandes questions pour les fondateurs de cette théorie. J'avais une certaine appréhension en Occident et ces scientifiques qui ont développé les mathématiques financières à une époque où l'économétrie était considérée comme une bourgeoisie corrompue en Union soviétique. Il me semblait que nous étions très loin derrière, et quelque part en Europe et en Amérique, les dieux de la finance étaient assis, qui connaissaient le Graal sacré de la vérité.

Maintenant, je comprends que les scientifiques européens et américains ne sont pas très différents des nôtres, la seule différence est dans l'échelle du charlatanisme. Nos scientifiques sont assis dans un château en ivoire, ils écrivent des bêtises et reçoivent des subventions d'un montant de 500 mille roubles. En Occident, environ les mêmes scientifiques sont assis dans le même château d'ivoire, ils écrivent sur le même non-sens et obtiennent un «nobel» et des subventions d'un montant de 500 000 dollars pour cela. C’est toute la différence.

Pour le moment, je n'ai pas une vision claire du sujet de mes recherches. Il est faux de dire que «tous les hedge funds utilisent le trading par paires» car la plupart des hedge funds font également faillite.

Malheureusement, vous devez toujours penser et prendre des décisions de votre propre chef, surtout lorsque nous risquons de l'argent.