La programmation dynamique a la réputation de la méthode que vous étudiez à l'université, et vous ne vous en souvenez que lors des entretiens. Mais en fait, la méthode est applicable dans de nombreuses situations. En fait, c'est une technique pour résoudre efficacement des problèmes qui peuvent être divisés en de nombreuses sous-tâches hautement répétitives .

Dans l'article, je vais montrer une application réelle intéressante de la programmation dynamique - la tâche de sculpture de couture. La tâche et la méthodologie sont décrites en détail dans les travaux d'Avidan et Shamir «Couper les coutures pour redimensionner les images en fonction du contenu» (article du domaine public).

Ceci fait partie d'une série d'articles sur la programmation dynamique. Si vous souhaitez peaufiner les méthodes, consultez l' introduction illustrée à la programmation dynamique .

Redimensionner l'image en fonction du contenu

Pour résoudre un problème réel à l'aide de la programmation dynamique, vous devez le formuler correctement. Cette section décrit les préréglages nécessaires pour la tâche sélectionnée.

Les auteurs de l'article d'origine décrivent le redimensionnement d'image orienté contenu, c'est-à-dire la modification de la largeur ou de la hauteur de l'image en fonction du contenu. Voir le travail original pour plus de détails, et je propose un bref aperçu. Supposons que vous souhaitiez redimensionner une photo d'un internaute:


Vue de dessus d'un surfeur au milieu d'un océan calme, avec des vagues turbulentes à droite. Photo: Kiril Dobrev sur Pixabay

Comme décrit en détail dans l'article, il existe plusieurs façons de réduire la largeur de l'image: ce sont le recadrage et la mise à l'échelle standard, avec leurs inconvénients inhérents, ainsi que la suppression des colonnes de pixels du milieu. Comme vous pouvez l'imaginer, cela laisse une couture visible sur la photo, où l'image de gauche et de droite ne correspond pas. Et de cette façon, vous ne pouvez supprimer qu'une quantité limitée d'images.


Une tentative de réduire la largeur en coupant le côté gauche et en coupant le bloc du milieu. Ce dernier laisse une couture visible.

Avidan et Shamir dans l'article décrivent la nouvelle technique de «sculpture de couture». Il identifie d'abord les zones «à faible énergie» moins importantes, puis calcule les «coutures» à faible énergie qui traversent l'image. Dans le cas d'une réduction de la largeur de l'image, une couture verticale est déterminée du haut de l'image vers le bas, qui sur chaque ligne se décale vers la gauche ou la droite de pas plus d'un pixel.

Sur la photo du surfeur, la couture la moins énergivore traverse le milieu de l'image, où l'eau est la plus silencieuse. Cela est conforme à notre intuition.


La couture la plus basse énergie trouvée dans l'image de l'internaute est représentée avec une ligne rouge de cinq pixels de large pour la visibilité, bien qu'en fait la couture ne soit que d'un pixel de large.

Après avoir déterminé la couture avec le moins d'énergie, puis l'enlever, nous réduisons la largeur de l'image d'un pixel. Répéter ce processus encore et encore réduit considérablement la largeur de la photo entière.


Image du surfeur après réduction de la largeur de 1024 pixels

Encore une fois, l'algorithme a logiquement supprimé l'eau calme au milieu, ainsi que sur le côté gauche de la photo. Mais contrairement au recadrage, la texture de l'eau à gauche est préservée et il n'y a pas de transitions nettes. Certes, vous pouvez trouver des transitions imparfaites au centre, mais en gros, le résultat semble naturel.

Définition de l'énergie de l'image

La magie est de trouver la couture la plus basse en énergie. Pour ce faire, nous attribuons d'abord de l'énergie à chaque pixel de l'image. Ensuite, nous utilisons la programmation dynamique pour trouver le chemin à travers l'image avec le moins d'énergie - cet algorithme sera discuté en détail dans la section suivante. Voyons d'abord comment attribuer des valeurs d'énergie aux pixels.

L'article scientifique discute plusieurs fonctions énergétiques et leurs différences. Ne compliquons pas cela et prenons une fonction qui capture simplement la quantité de changement de couleur autour de chaque pixel. Pour compléter l'image, je décrirai la fonction d'énergie plus en détail au cas où vous voudriez l'implémenter vous-même, mais ce n'est qu'un préréglage pour les calculs de programmation dynamique ultérieurs.


À gauche, trois pixels du foncé au clair. La différence entre le premier et le dernier est grande. Trois pixels sombres à droite avec une légère différence d'intensité des couleurs

Pour calculer l'énergie d'un pixel spécifique, regardez les pixels à gauche et à droite de celui-ci. Côté composants, nous calculons le carré de la distance entre eux, c'est-à-dire le carré de la différence entre les composants rouge, vert et bleu, puis nous les ajoutons. Nous faisons de même pour les pixels au-dessus et en dessous du centre. Enfin, additionnez les distances horizontales et verticales.

$$

$$| \ Delta x | ^ 2 = (\ Delta r_x) ^ 2 + (\ Delta g_x) ^ 2 + (\ Delta b_x) ^ 2$$

$$

$$| \ Delta y | ^ 2 = (\ Delta r_y) ^ 2 + (\ Delta g_y) ^ 2 + (\ Delta b_y) ^ 2$$

$$

$$e (x, y) = | \ Delta x | ^ 2 + | \ Delta y | ^ 2$$

La seule mise en garde - disons, si un pixel est sur le bord gauche, il n'y a pas de voisin sur la gauche. Dans ce cas, nous comparons uniquement avec le bon pixel. Des vérifications similaires sont effectuées pour les pixels sur les bords supérieur, droit et inférieur.

La fonction d'énergie est grande si les pixels voisins sont de couleurs très différentes et petite si elles sont similaires.


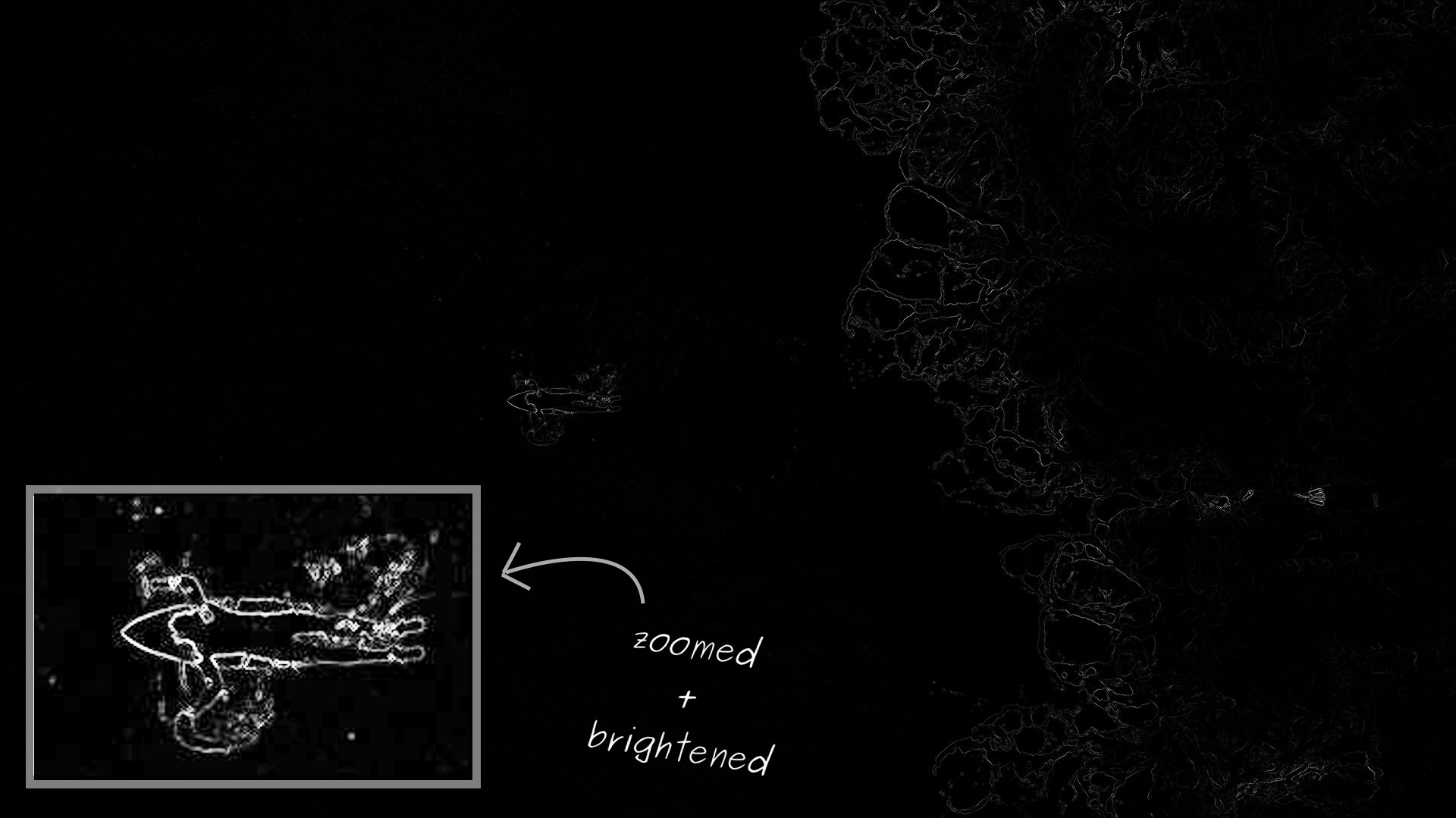L’énergie de chaque pixel dans la photo d’un internaute: plus il est clair - plus il est élevé. Comme prévu, le surfeur a l'énergie la plus élevée au milieu et les vagues turbulentes à droite

La fonction énergie fonctionne bien sur une photo de surfeur. Cependant, cela prend une très large gamme de valeurs. Par conséquent, lors du rendu, il semble que dans la plupart des photos, les pixels aient une énergie nulle. En fait, il y a tout simplement des valeurs très faibles par rapport aux régions où l'énergie est la plus élevée. Pour simplifier la visualisation, j'ai zoomé sur l'internaute et mis en évidence cette zone.

Recherche de coutures basse énergie avec programmation dynamique

En calculant l'énergie de chaque pixel, nous pouvons trouver la couture avec l'énergie la plus faible du haut de l'image vers le bas. La même analyse s'applique aux coutures horizontales pour réduire la hauteur de l'image d'origine. Cependant, nous nous concentrerons sur les verticales.

Commençons par la définition:

• Une couture est une séquence de pixels, un pixel par ligne. La condition est qu'entre deux lignes consécutives, les coordonnées $$$x$change de pas plus d'un pixel. Cela préserve la séquence de couture.
  
• La couture avec l'énergie la plus faible est celle dont l'énergie totale sur tous les pixels de la couture est minimisée.

Il est important de noter que le joint avec l'énergie la plus basse ne passe pas nécessairement par tous les pixels avec l'énergie la plus basse. L'énergie totale de tous, pas des pixels individuels, est prise en compte.


L'approche gourmande ne fonctionne pas. En choisissant un pixel basse énergie à un stade précoce, on se retrouve coincé dans la zone haute énergie de l'image (chemin rouge à droite)

Comme vous pouvez le voir, vous ne pouvez pas simplement sélectionner le pixel à énergie la plus basse sur la ligne suivante.

Nous divisons le problème en sous-tâches

Le problème avec l'approche gourmande est que lorsque nous décidons de la prochaine étape, nous ne prenons pas en compte le reste de la couture à venir. Nous ne pouvons pas regarder vers l'avenir, mais nous pouvons prendre en compte tout ce que nous savons déjà.

Tournons la tâche à l'envers. Au lieu de choisir entre plusieurs pixels pour continuer une couture, nous choisirons entre plusieurs coutures pour aller à un pixel . Ce que nous devons faire, c'est prendre chaque pixel et choisir entre les pixels de la ligne ci-dessus, d'où peut provenir la couture. Si chacun des pixels de la ligne ci-dessus code le chemin parcouru jusqu'à ce point, alors nous examinons essentiellement l'historique complet jusqu'à ce point.


Pour chaque pixel, nous étudions trois pixels dans la ligne ci-dessus. Choix fondamental - laquelle des coutures continuer?

Cela suppose une sous-tâche pour chaque pixel de l'image. La sous-tâche doit trouver le meilleur chemin vers un pixel spécifique, c'est donc une bonne idée d'associer à chaque pixel l'énergie de la couture à faible énergie qui se termine par ce pixel .

Contrairement à l'approche gourmande, l'approche ci-dessus essaie essentiellement tous les chemins possibles à travers l'image. C'est juste que lors de la vérification de tous les chemins possibles, les mêmes sous-tâches sont résolues encore et encore, ce qui fait de cette approche une option idéale pour la programmation dynamique.

Définition d'une relation de récurrence

Comme d'habitude, nous devons maintenant formaliser l'idée dans une relation récursive. Il y a une sous-tâche correspondant à chaque pixel de l'image d'origine, donc les entrées de notre relation de récurrence peuvent être juste des coordonnées $$$x$et $$$y$de ce pixel. Cela fournit des entrées entières, ce qui facilite l'organisation des sous-tâches, ainsi que la possibilité de stocker les valeurs précédemment calculées dans un tableau à deux dimensions.

Définir une fonction $$$M (x, y)$, qui représente l'énergie de la couture verticale avec le moins d'énergie. Il commence en haut de l'image et se termine par un pixel $$$(x, y)$. Le titre $$$M$sélectionnés comme dans l'article scientifique d'origine.

Tout d'abord, vous avez besoin d'une version de base. Toutes les coutures qui se terminent sur la ligne supérieure ont une longueur d'un seul pixel. Ainsi, une couture avec une énergie minimale n'est qu'un pixel avec une énergie minimale:

$$

$$M (x, 0) = e (x, 0)$$

Pour les pixels dans les lignes restantes, regardez les pixels en haut. La couture devant être continue, nous ne prenons en compte que trois pixels situés en haut à gauche, en haut et en haut à droite. À partir d'eux, nous sélectionnons la couture avec l'énergie la plus faible, qui se termine par l'un de ces pixels, et ajoutons l'énergie du pixel actuel:

$$

$$M (x, y) = e (x, y) + \ min \ begin {cases} M (x - 1, y - 1) \\ M (x, y - 1) \\ M (x + 1, y - 1) \ end {cases}$$

En tant que situation limite, considérons le cas où le pixel actuel se trouve sur le bord gauche ou droit de l'image. Dans ces cas, nous omettons $$$M (x-1, y-1)$pour les pixels sur le bord gauche ou $$$M (x + 1, y-1)$sur le bord droit.

Enfin, vous devez extraire l'énergie de la couture basse énergie, qui couvre toute la hauteur de l'image. Cela signifie que nous regardons la ligne inférieure de l'image et sélectionnons la couture la plus basse qui se termine à l'un de ces pixels. Pour photo large $$$W$et grand $$$H$pixels:

$$

$$\ min_ {0 \ le x <W} M (x, H - 1)$$

Nous avons donc obtenu une relation de récurrence avec toutes les propriétés nécessaires:

• Une relation de récurrence a des entrées entières.
  
• La réponse finale est facile à extraire de la relation.
  
• Le rapport dépend de soi.

Vérification de la sous-tâche DAG (graphe acyclique orienté)

Depuis chaque sous-tâche $$$M (x, y)$correspond à un pixel de l'image d'origine, le graphique des dépendances est très facile à visualiser. Placez-les simplement sur une grille à deux dimensions, comme dans l'image originale!


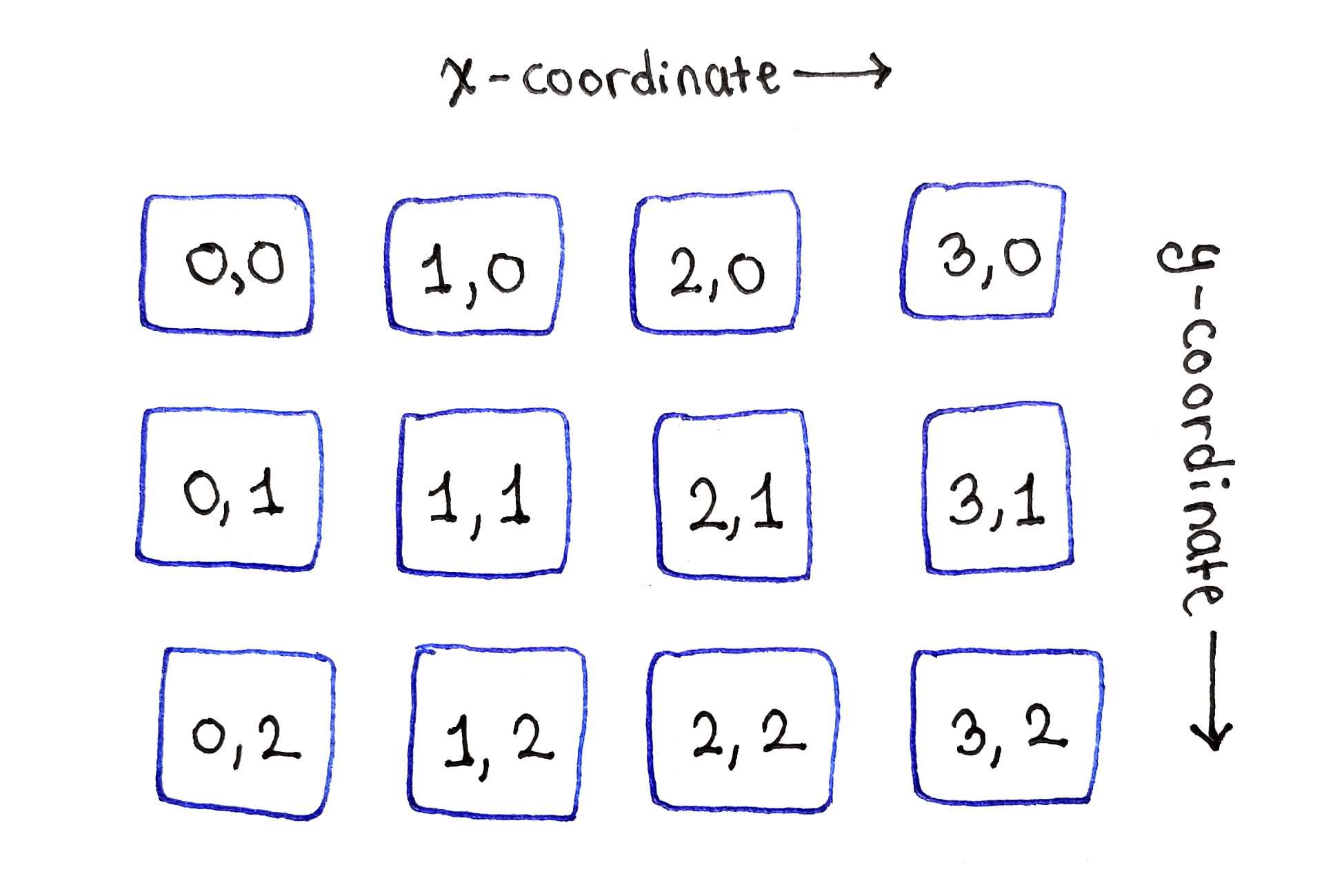Les sous-tâches sont situées dans une grille à deux dimensions, comme les pixels de l'image d'origine

Comme il ressort du scénario de base de la relation de récurrence, la ligne supérieure des sous-tâches peut être initialisée avec les valeurs d'énergie des pixels individuels.


La ligne supérieure est indépendante des autres sous-tâches. Notez l'absence de flèches dans la rangée supérieure des cellules

Dans la deuxième ligne, les dépendances commencent à apparaître. Premièrement, dans la cellule la plus à gauche de la deuxième rangée, nous sommes confrontés à une situation frontalière. Puisqu'il n'y a pas de cellules à gauche, la cellule $$$(1,0)$ne dépend que des cellules situées directement au-dessus et en haut à droite. La même chose se produira plus tard avec la cellule la plus à gauche dans la troisième rangée.


Les sous-tâches sur le bord gauche dépendent uniquement de deux sous-tâches au-dessus d'eux

Dans la deuxième cellule de la deuxième rangée (1,1), nous voyons la manifestation la plus typique de la relation de récurrence. Cette cellule dépend de trois cellules: en haut à gauche, juste au-dessus et en haut à droite. Cette structure de dépendance s'applique à toutes les cellules «intermédiaires» de la deuxième ligne et des suivantes.


Les sous-tâches entre les bords gauche et droit dépendent des trois sous-tâches en haut

Enfin, la cellule sur le bord droit représente la deuxième situation limite. Puisqu'il n'y a plus de cellules à droite, cela ne dépend que des cellules directement en haut et en haut à gauche.


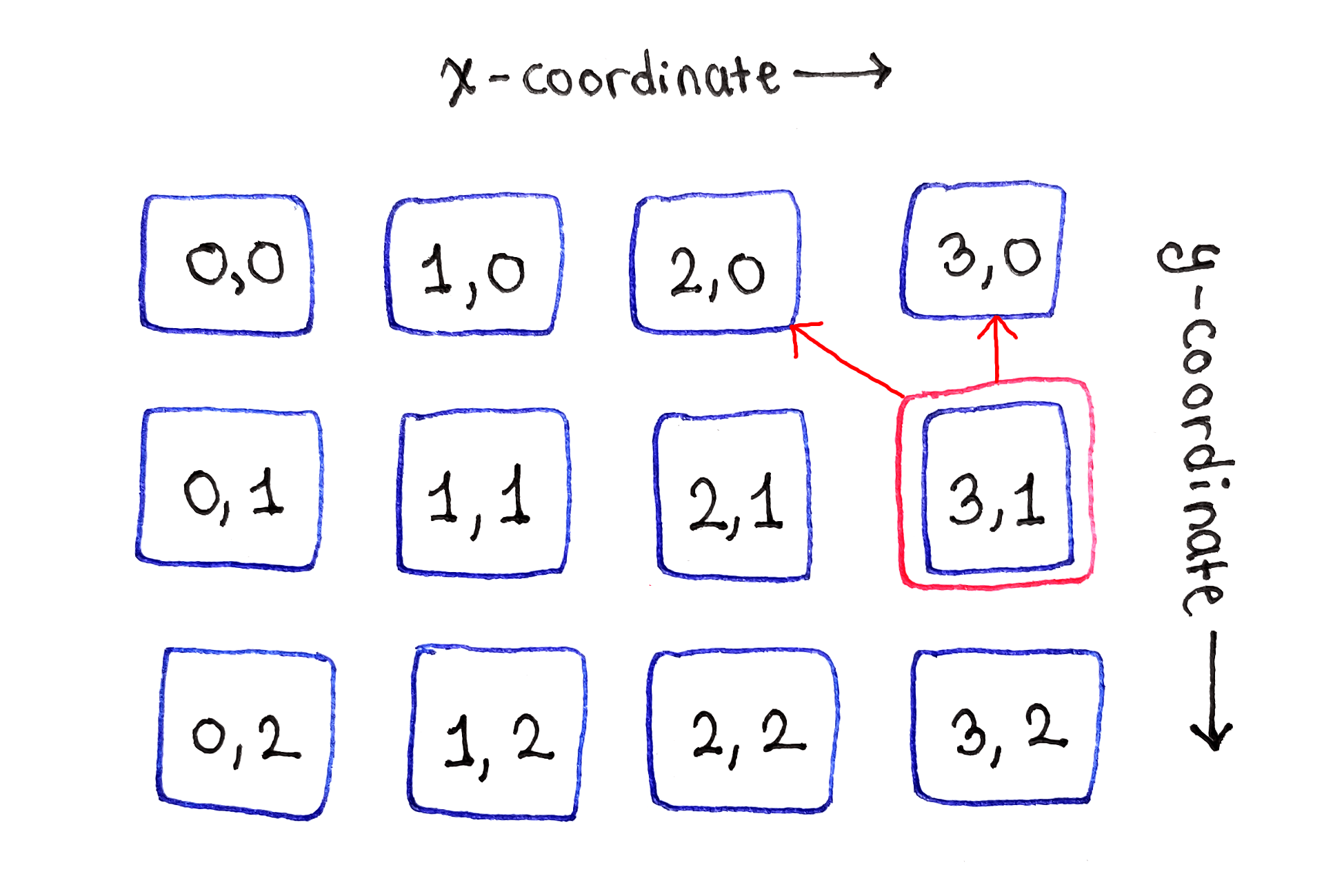Les sous-tâches sur le bord droit ne dépendent que de deux cellules en haut

Le processus est répété pour toutes les lignes suivantes.


Comme il y a beaucoup de flèches dans le graphique des dépendances, cette animation montre tour à tour les dépendances pour chaque sous-tâche

Un graphique de dépendance complet vous fait peur avec un grand nombre de flèches, mais les regarder une à la fois aide à établir des modèles explicites.

Mise en œuvre ascendante

Après avoir effectué cette analyse, nous avons obtenu l'ordre de traitement:

• Allez du haut de l'image vers le bas.
  
• Chaque ligne peut agir dans n'importe quel ordre. Le choix naturel est d'aller de gauche à droite.

Étant donné que chaque ligne dépend uniquement de la précédente, vous devez enregistrer uniquement deux lignes de données: une pour la ligne précédente et une pour la ligne actuelle. En se déplaçant de gauche à droite, nous pouvons même ignorer les éléments individuels de la ligne précédente lorsqu'ils sont utilisés. Cependant, cela complique l'algorithme, car il devra déterminer quelles parties de la ligne précédente peuvent être supprimées.

Dans le code Python suivant, l'entrée est une liste de lignes, où chaque ligne contient une liste de nombres représentant les énergies de pixel individuelles dans cette ligne. L'entrée est appelée pixel_energies , et pixel_energies[y][x] représente l'énergie du pixel en coordonnées $$$(x, y)$.

Commençons par calculer l'énergie des coutures de la rangée supérieure, simplement en copiant les énergies des pixels individuels dans la rangée supérieure:

 previous_seam_energies_row = list(pixel_energies[0]) 

Ensuite, nous parcourons les lignes d'entrée restantes, calculant les énergies de couture pour chaque ligne. La partie la plus «difficile» consiste à déterminer à quels éléments de la ligne précédente se référer, car il n'y a pas de pixels à gauche du bord gauche ou à droite du bord droit.

À chaque itération, une nouvelle liste des énergies de couture pour la ligne actuelle est créée. À la fin de l'itération, nous remplaçons les données de la ligne précédente par les données de la ligne actuelle pour l'itération suivante. Voici comment nous supprimons la ligne précédente:

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_seam_energy = pixel_energy + \ min(previous_seam_energies_row[x_i] for x_i in x_range) seam_energies_row.append(min_seam_energy) previous_seam_energies_row = seam_energies_row 

Par conséquent, previous_seam_energies_row contient l'énergie de couture pour la ligne de fond. Nous trouvons la valeur minimale dans cette liste - et c'est la réponse!

 min(seam_energy for seam_energy in previous_seam_energies_row) 

Vous pouvez tester cette implémentation en encapsulant le code dans une fonction, puis en l'appelant avec le tableau à deux dimensions que vous avez créé. L'entrée suivante a été choisie pour que l'approche gourmande échoue, avec une couture évidente avec l'énergie la plus basse:

 ENERGIES = [ [9, 9, 0, 9, 9], [9, 1, 9, 8, 9], [9, 9, 9, 9, 0], [9, 9, 9, 0, 9], ] print(min_seam_energy(ENERGIES)) 

Complexité spatiale et temporelle

Chaque pixel de l'image d'origine correspond à une sous-tâche. Pour chacune des sous-tâches, il n'y a pas plus de trois dépendances, donc la résolution de chacune d'entre elles implique une quantité constante de travail. La dernière rangée a lieu deux fois. Donc pour une image large $$$W$et grand $$$H$la complexité temporelle des pixels est $$$O (L × H + W)$.

À chaque instant, nous avons deux listes: une pour la ligne précédente et une pour la ligne actuelle. Dans le premier $$$W$éléments, et le second augmente progressivement pour $$$W$. Ainsi, la complexité spatiale est égale à $$$O (2 W)$c'est juste $$$O (w)$.

Notez que si nous supprimions réellement les éléments de données de la ligne précédente, nous raccourcirions la liste des éléments de la ligne précédente à peu près à la même vitesse que la liste de la ligne actuelle s'allonge. Ainsi, la complexité spatiale restera $$$O (w)$. Bien que la largeur puisse varier, ce n'est généralement pas si important.

Pointeurs arrière basse énergie

Nous avons donc trouvé la signification de la couture basse énergie, mais que faire de ces informations? Après tout, en fait, nous ne nous soucions pas de l'importance de l'énergie, mais de la couture elle-même! Le problème est qu'il n'y a aucun moyen de revenir du pixel final au reste de la couture.

C'est ce que j'ai manqué dans les articles précédents, mais il en va de même pour de nombreux problèmes de programmation dynamique. Par exemple, si vous vous souvenez de la tâche d'un voleur de maison , nous avons trouvé la valeur maximale pour le montant du vol, mais pas quelles maisons spécifiques doivent être cambriolées pour obtenir ce montant.

Représentation des pointeurs arrière

Réponse générale: stockez les pointeurs . Dans la tâche de couper les coutures, nous avons besoin non seulement de la valeur de l'énergie de la couture à chaque pixel. Vous devez également savoir lequel des pixels de la ligne précédente a conduit à cette énergie. En stockant ces informations, nous pouvons suivre les pointeurs inverses jusqu'à la ligne supérieure, en obtenant les coordonnées de tous les pixels qui composent le joint avec le moins d'énergie.

Tout d'abord, créez une classe pour stocker l'énergie et les pointeurs arrière. L'énergie sera utilisée pour calculer les sous-tâches. Puisque le pointeur arrière détermine quel pixel de la ligne précédente a donné l'énergie actuelle, nous pouvons l'imaginer simplement comme la coordonnée x.

 class SeamEnergyWithBackPointer(): def __init__(self, energy, x_coordinate_in_previous_row=None): self.energy = energy self.x_coordinate_in_previous_row = x_coordinate_in_previous_row 

Le résultat du calcul pour chaque sous-tâche ne sera pas seulement un nombre, mais une instance de cette classe.

Stockage du pointeur arrière

Au final, il faut remonter sur toute la hauteur de l'image, en suivant les signes inverses pour restaurer la couture avec le moins d'énergie. Malheureusement, cela signifie que vous devez stocker des pointeurs pour tous les pixels de l'image, pas seulement la ligne précédente.

Pour ce faire, nous enregistrons simplement le résultat complet de toutes les sous-tâches, bien qu'il soit techniquement possible d'abandonner les énergies numériques de la couture des lignes précédentes. Les résultats sont stockés dans un tableau à deux dimensions, qui ressemble au tableau d'entrée.

Commençons par la première ligne, qui ne contient que des énergies de pixels individuelles. Puisqu'il n'y a pas de ligne précédente, tous les pointeurs arrière sont manquants, mais pour des SeamEnergyWithBackPointers de cohérence, nous conserverons toujours les instances de SeamEnergyWithBackPointers :

 seam_energies = [] # Initialize the top row of seam energies by copying over the top row of # the pixel energies. There are no back pointers in the top row. seam_energies.append([ SeamEnergyWithBackPointer(pixel_energy) for pixel_energy in pixel_energies[0] ]) 

La boucle principale fonctionne essentiellement de la même manière que l'implémentation précédente, avec les différences suivantes:

• Les données de la ligne précédente contiennent des instances de SeamEnergyWithBackPointer , par conséquent, lors du calcul de la valeur du taux de récurrence, vous devez rechercher l'énergie de la couture à l'intérieur de ces objets.
  
• En enregistrant les données pour le pixel actuel, vous devez créer une nouvelle instance de SeamEnergyWithBackPointer . Ici, nous allons stocker l'énergie de couture pour le pixel actuel, ainsi que la coordonnée x de la ligne précédente, utilisée pour calculer l'énergie de couture actuelle.
  
• À la fin de chaque ligne, au lieu de supprimer les données de la ligne précédente, nous ajoutons simplement les données de la ligne actuelle à seam_energies .

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_parent_x = min( x_range, key=lambda x_i: seam_energies[y - 1][x_i].energy ) min_seam_energy = SeamEnergyWithBackPointer( pixel_energy + seam_energies[y - 1][min_parent_x].energy, min_parent_x ) seam_energies_row.append(min_seam_energy) seam_energies.append(seam_energies_row) 

Suivez les panneaux

Maintenant, toute la table des sous-tâches est remplie et nous pouvons restaurer la couture avec le moins d'énergie. Nous commençons par chercher la coordonnée x dans la ligne du bas, qui correspond au joint avec le moins d'énergie:

 # Find the x coordinate with minimal seam energy in the bottom row. min_seam_end_x = min( range(len(seam_energies[-1])), key=lambda x: seam_energies[-1][x].energy ) 

Maintenant, allez du bas de l'image vers le haut, en changeant $$$y$de len(seam_energies) - 1 à zéro. À chaque itération, ajoutez la paire actuelle $$$(x, y)$à la liste représentant notre couture, puis définissez la valeur $$$x$pour l'objet vers lequel pointe SeamEnergyWithBackPointer dans la ligne actuelle.

 # Follow the back pointers to form a list of coordinates that form the # lowest-energy seam. seam = [] seam_point_x = min_seam_end_x for y in range(len(seam_energies) - 1, -1, -1): seam.append((seam_point_x, y)) seam_point_x = \ seam_energies[y][seam_point_x].x_coordinate_in_previous_row seam.reverse() 

Ainsi, la couture est construite vers le haut, la liste peut ensuite être lue dans l'ordre inverse, si vous avez besoin de coordonnées de haut en bas.

Complexité spatiale et temporelle

La complexité temporelle est similaire à la précédente, car nous devons encore traiter chaque pixel une fois. Après avoir regardé la dernière ligne et trouvé l'articulation avec le moins d'énergie, nous remontons ensuite toute la hauteur de l'image pour restaurer l'articulation. Donc pour l'image $$$L × H$la complexité du temps est égale $$$O (L × H + L + H)$.

En ce qui concerne le volume, nous gardons toujours une quantité constante de données pour chaque sous-tâche, mais maintenant nous ne supprimons aucune donnée. Nous utilisons donc le volume $$$O (L × H)$.

Élimination des coutures à faible énergie

Dès que le joint vertical avec l'énergie la plus basse est trouvé, nous pouvons simplement copier les pixels de l'image d'origine vers une nouvelle. Chaque ligne de la nouvelle image contient tous les pixels de la ligne correspondante de l'image d'origine, à l'exception du pixel de la couture avec l'énergie la plus faible. Puisque nous supprimons un pixel dans chaque ligne, à partir de l'image $$$L × H$alors on obtient l'image $$$(W - 1) × H$.

Nous pouvons répéter ce processus en racontant la fonction d'énergie dans la nouvelle image et en trouvant la couture la plus basse sur elle. Il semble tentant de trouver plus d'une couture à faible énergie dans l'image d'origine, puis de les supprimer toutes en même temps. Le problème est que les deux coutures peuvent se croiser. Lorsque le premier est supprimé, le second devient invalide car il manque un ou plusieurs pixels.


Animation du processus de retrait des coutures. Mieux vaut regarder en plein écran pour une vue plus claire des coutures

Chaque image de la vidéo est une image à chaque itération avec visualisation superposée de la couture avec le moins d'énergie.

Un autre exemple

L'article avait beaucoup d'explications détaillées, alors terminons avec une série de belles photos! La photo suivante montre une formation rocheuse dans le parc national des Arches:


Formation rocheuse avec un trou dans le parc national des Arches. Photo: Mike Goad sur Flickr

Fonction énergétique pour cette image:


L'énergie de chaque pixel de la photo: plus elle est claire - plus elle est élevée. Notez la haute énergie autour du bord du trou

À la suite du calcul, une telle couture avec l'énergie la plus basse est obtenue. Notez qu'il passe à travers le rocher sur la droite, entrant directement dans la formation rocheuse où la partie illuminée au sommet du rocher correspond à la couleur du ciel. Vous devriez peut-être choisir une meilleure fonction énergétique!


La couture la plus basse énergie trouvée dans l'image est représentée avec une ligne rouge de cinq pixels de large pour la visibilité, bien qu'en réalité la couture ne soit que d'un pixel de large

Enfin, l'image de l'arc après redimensionnement:


Arch après compression à 1024 pixels

Le résultat n'est certainement pas parfait: de nombreux bords de la montagne de l'image d'origine sont déformés. L'une des améliorations peut être la mise en œuvre de l'une des autres fonctions énergétiques répertoriées dans l'article scientifique.

---

Bien que la programmation dynamique soit généralement discutée en théorie, c'est une méthode pratique utile pour résoudre des problèmes complexes. Dans cet article, nous avons examiné l'une des applications de la programmation dynamique: redimensionner des images pour les adapter au contenu en coupant les coutures.

Nous avons appliqué les mêmes principes de division d'une tâche en sous-tâches plus petites, en analysant les dépendances entre ces sous-tâches, puis en résolvant les sous-tâches dans un ordre qui minimise la complexité spatiale et temporelle de l'algorithme. De plus, nous avons étudié l'utilisation de pointeurs inverses non seulement pour trouver la valeur énergétique de la couture optimale, mais également pour déterminer les coordonnées de chaque pixel qui constituait cette valeur. Ensuite, nous avons appliqué ces parties à un problème réel, qui nécessite un certain pré et post-traitement pour une utilisation vraiment efficace de l'algorithme de programmation dynamique.