À l'école, lorsque nous avons résolu des équations ou considéré des formules, nous avons essayé de les réduire d'abord plusieurs fois, par exemple, Z = X - (Y + X) réduit à Z = -Y . Dans les compilateurs modernes, il s'agit d'un sous-ensemble des optimisations dites de judas, dans lesquelles, en gros, un ensemble de modèles nous réduisons les expressions, remplaçons les instructions par des instructions plus rapides pour un processeur particulier, etc. Dans cet article, j'ai compilé une collection de ces optimisations trouvées dans les sources LLVM, GCC et .NET Core (CoreCLR).
Commençons par des exemples simples:
X * 1 => X -X * -Y => X * Y -(X - Y) => Y - XX * Z - Y * Z => Z * (X - Y)
vérifiez le dernier exemple en C ++ et en C #:
int Test(int x, int y, int z) { return x * z - y * z;
et regardez l'assembleur de Clang (LLVM), GCC, MSVC et .NET Core:

Les trois compilateurs C ++ (GCC, Clang et MSVC) ont réduit une multiplication (nous ne voyons qu'une seule instruction imul ). C # ne l'a pas fait avec RyuJIT, mais ne vous précipitez pas pour le gronder, c'est juste que cette classe d'optimisations est disponible dans une composition limitée là-bas. Pour vous faire comprendre, l'implémentation de l'intégralité de la transformation InstCombine dans LLVM prend plus de 30k lignes de code (+ 20k lignes sur DAGCombiner.cpp), de plus, cette transformation entraîne souvent une longue compilation. Soit dit en passant, le site responsable de cette optimisation est là. GCC a une DSL spéciale qui décrit le piphole d'optimisation, voici un extrait ).
J'ai décidé, pour les besoins de l'article, d'essayer de mettre en œuvre cette optimisation en C # JIT (tenir ma bière):
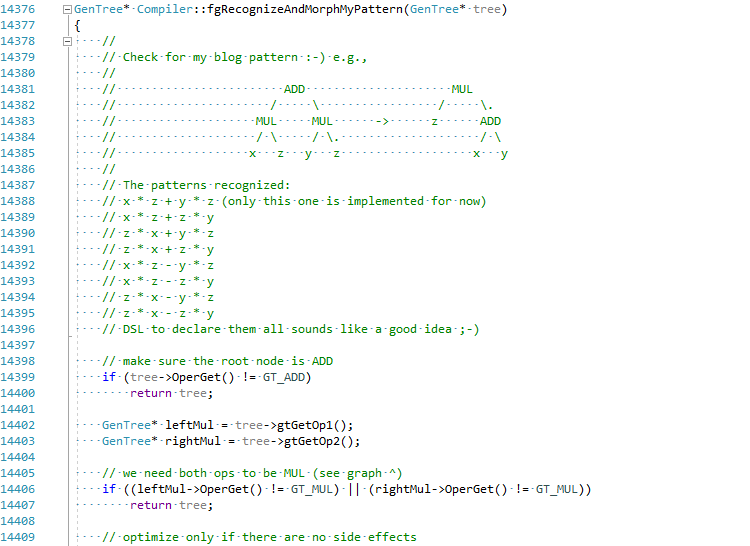
Le commit complet peut être vu ici EgorBo / coreclr . Vérifions maintenant mon amélioration (dans Visual Studio 2019 + Disasmo:
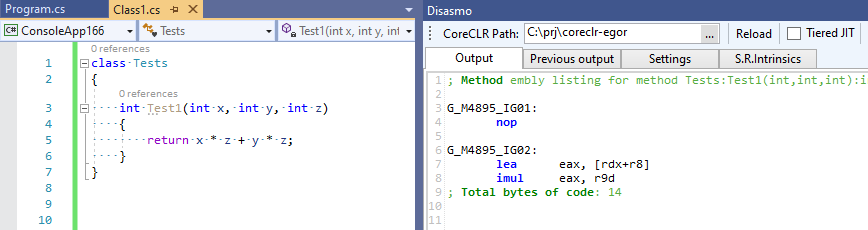
Ça marche! lea + imul au lieu d' imul , imul et add .
Revenons à C ++ et suivons cette optimisation dans Clang. Pour ce faire, demandez à clang de nous donner l'IR LLVM initial via -emit-llvm -g0 , puis de le donner à LLVM à l'optimiseur, en utilisant les -O2 -print-before-all -print-after-all afin de capturer le moment exact de la transformation supprime la multiplication de l'ensemble -O2 (tout cela peut être vu sur la merveilleuse ressource godbolt.org ):
; *** IR Dump Before Combine redundant instructions *** define dso_local i32 @_Z5Case1iii(i32, i32, i32) { %4 = mul nsw i32 %0, %2 %5 = mul nsw i32 %1, %2 %6 = sub nsw i32 %4, %5 ret i32 %6 } ; *** IR Dump After Combine redundant instructions *** define dso_local i32 @_Z5Case1iii(i32, i32, i32) { %4 = sub i32 %0, %1 %5 = mul i32 %4, %2 ret i32 %5 }
Vous pouvez également vous amuser sur godbolt avec les outils LLVM - opt (optimiseur) et llc (pour compiler LLVM IR en asm):

Retour aux exemples. J'ai trouvé ce très bel exemple dans GCC.
X == C - X => false if C is odd
Et c'est vrai: si 4 == 8 - 4 . Mais si au lieu de 8 vous en écrivez un impair, alors vous ne pouvez pas trouver un tel X pour que l'égalité soit remplie:
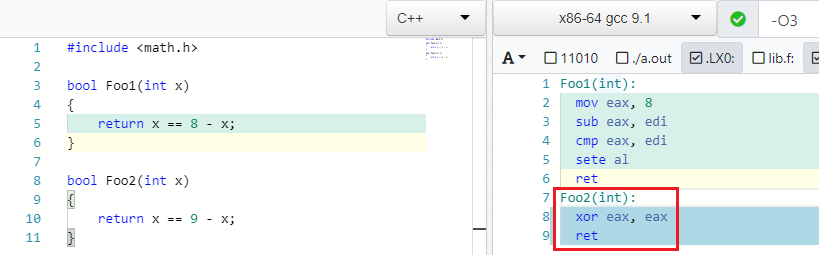
IEEE754 contre-attaque
De nombreuses optimisations fonctionnent pour différents types de données, par exemple, byte , unsigned , unsigned , float , double . Avec ce dernier, les choses ne sont pas si simples et les optimisations sont gérées par la spécification IEEE754, qui deviendra folle si vous réduisez A - B - A en -B ou (A * B) * C réorganisant en A * (B * C) t. à. les opérations ne sont pas associatives. Mais il y a un mode spécial dans les compilateurs modernes qui vous permet de négliger les valeurs de spécification et de limite (NaN, + -Inf, + -0.0) dans de tels cas et d'effectuer des optimisations en toute sécurité - c'est Fast Math (ma demande de PR pour ajouter un tel mode à C # peut être trouvée ici )
Comme vous pouvez le voir dans -ffast-math il n'y a plus deux vsubss :
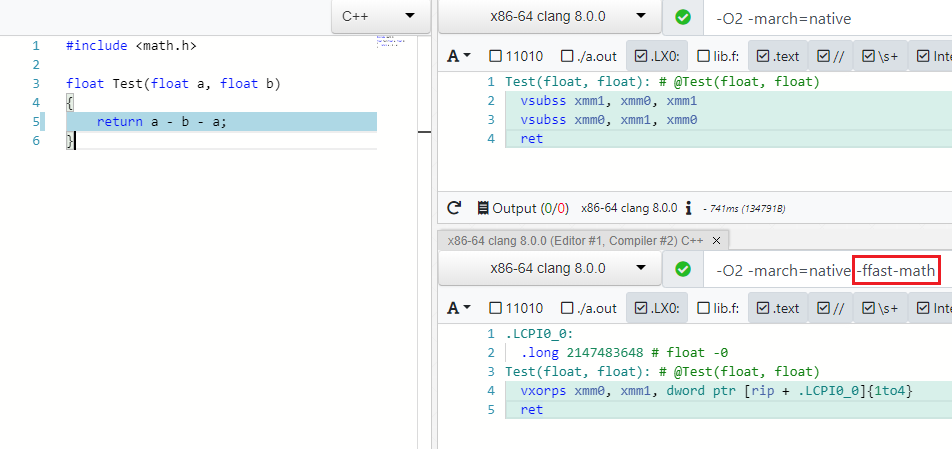
En plus des expressions, les optimiseurs prennent également en compte le jonglage avec les fonctions mathématiques de math.h , par exemple, le produit des modules du nombre X est égal au produit du nombre X:
abs(X) * abs(X) => X * X
La racine carrée est toujours positive:
sqrt(X) < Y => false, if Y is negative. sqrt(X) < 0 => false
Pourquoi calculer la racine, s'il est possible au stade de la compilation de calculer le carré de la constante à droite?:
sqrt(X) > C => X > C * C

Plus d'opérations root:
sqrt(X) == sqrt(Y) => X == Y sqrt(X) * sqrt(X) => X sqrt(X) * sqrt(Y) => sqrt(X * Y) logN(sqrt(X)) => 0.5*logN(X)
Un peu plus de mathématiques à l'école:
expN(X) * expN(Y) -> expN(X + Y)
Et mon optimisation préférée:
sin(X) / cos(X) => tan(X)

Beaucoup d'opérations ennuyeuses et booléennes:
((a ^ b) | a) -> (a | b) (a & ~b) | (a ^ b) --> a ^ b ((a ^ b) | a) -> (a | b) (X & ~Y) |^+ (~X & Y) -> X ^ Y A - (A & B) into ~B & A X <= Y - 1 equals to X < Y A < B || A >= B -> true ... !
Optimisations de bas niveau
Il existe un ensemble d'optimisation qui, à première vue, n'a pas de sens avec t.z. mathématiciens, mais sont plus amicaux à repasser.
X / 2 => X * 0.5
remplacer la division par la multiplication:

Le fonctionnement de la multiplication de flotte présente généralement de meilleures caractéristiques de latence / débit que la division. Par exemple, voici les options pour Intel Haswell:

En mode mathématique non rapide, elle ne peut être utilisée que si la constante est une puissance de deux.
Au fait, j'ai récemment essayé d'ajouter une telle optimisation en C #. C'est-à-dire si, par exemple, vous devez ouvrir un fichier avec un modèle 3D et réduire toutes les coordonnées de 10 fois, alors * 0,1 gérera cette vitesse de 20 à 100% plus rapidement, ce qui peut être important.
La même justification pour:
X * 2 => X + X
Comparer avec zéro ( test ) est meilleur que comparer avec l'unité ( cmp ) - mon PR pour plus de détails est dotnet / coreclr # 25458 :
X >= 1 => X > 0 X < 1 => X <= 0 X <= -1 => X >= 0 X > -1 => X >= 0
Et comment aimez-vous cela:
pow(X, 0.5) => sqrt(x) pow(X, 0.25) => sqrt(sqrt(X)) pow(X, 2) => X * X ; 1 mul pow(X, 3) => X * X * X ; 2 mul

Que pensez-vous, combien d'opérations de multiplication avez-vous besoin pour compter le mod(X, 4) ou X * X * X * X ?
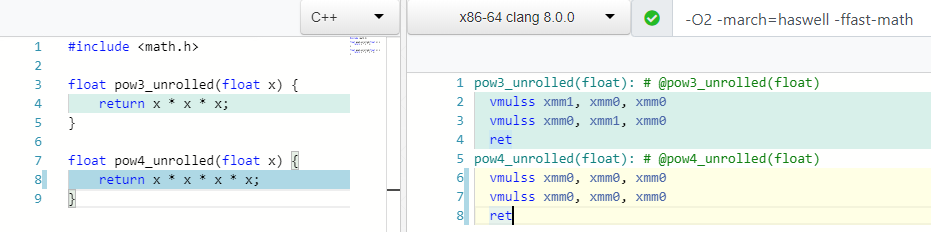
Deux! Ainsi que pour le calcul du 3ème degré, et dans le cas 4 nous n'utilisons qu'un seul registre xmm0 .
De nombreux processeurs prennent en charge une instruction spéciale (FMA), qui vous permet d'effectuer la multiplication et l'addition à la fois, tout en conservant la précision pendant la multiplication:
X * Y + Z => fmadd(X, Y, Z)

Deux autres de mes exemples préférés sont le pliage de certains algorithmes en une seule instruction (si le processeur le prend en charge):
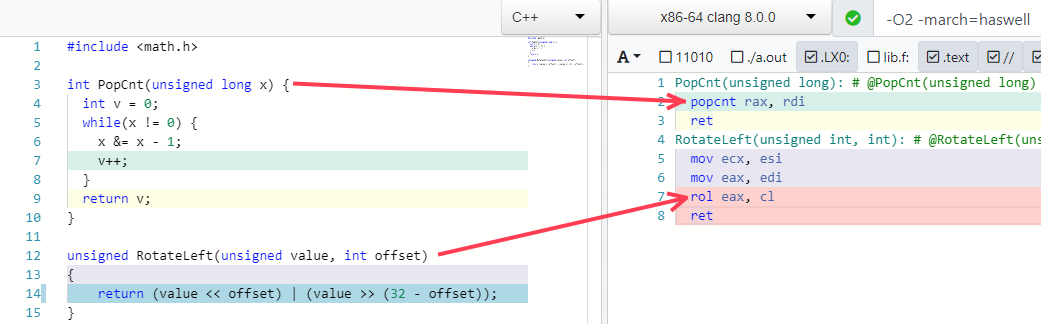
Pièges d'optimisation
Je pense que tout le monde comprend que vous ne pouvez pas vous précipiter et réduire les expressions pour trois raisons:
- Vous pouvez casser le code sur certaines valeurs limites, débordements, effets secondaires cachés, etc ... Bugzilla LLVM contient de nombreux bogues InstCombine.
- Idéalement, les optimisations devraient fonctionner ensemble dans une séquence spécifique.
- L'expression ou des parties de celle-ci que vous souhaitez réduire peuvent être utilisées ailleurs et leur réduction entraînera une dégradation des performances.
Regardons simplement un exemple pour le dernier paragraphe (espionné dans l'article Future Directions for Optimizing Compilers ).
Imaginez que nous ayons ce code:
int Foo1(int a, int b) { int na = -a; int nb = -b; return na + nb; }
nous devons faire trois opérations: 0 - a , 0 - b et na + nb . Mais l'optimiseur pour nous réduit cela à deux - return -(a + b); :
define dso_local i32 @_Z4Foo1ii(i32, i32) { %3 = add i32 %0, %1 ; a + b %4 = sub i32 0, %3 ; 0 - %3 ret i32 %4 }
Imaginez maintenant que nous devons écrire des valeurs intermédiaires na et nb dans des variables globales:
int x, y; int Foo2(int a, int b) { int na = -a; int nb = -b; x = na; y = nb; return na + nb; }
L'optimiseur trouve toujours ce modèle et supprime les opérations inutiles (de son point de vue) 0 - a et 0 - b , mais en fait il s'avère qu'elles sont nécessaires! nous écrivons les résultats de ces opérations "inutiles" dans des variables globales! Cela conduit à ce code:
define dso_local i32 @_Z4Foo2ii(i32, i32) { %3 = sub nsw i32 0, %0 ; 0 - a %4 = sub nsw i32 0, %1 ; 0 - b store i32 %3, i32* @x, align 4, !tbaa !2 store i32 %4, i32* @y, align 4, !tbaa !2 %5 = add i32 %0, %1 ; a + b %6 = sub i32 0, %5 ; 0 - %5 ret i32 %6 }
Quatre opérations mathématiques au lieu de trois! Notre optimiseur nous a fait défaut et n'était pas convaincu que les expressions intermédiaires qu'il optimisait étaient encore nécessaires à quelqu'un. Voyons maintenant la sortie de C # RuyJIT, dans laquelle il n'y a pas une telle optimisation intelligente:
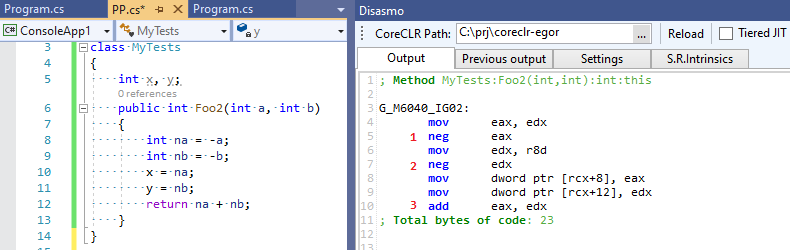
Trois opérations au lieu de quatre - C # s'est avéré être plus rapide que C ++ :-)!.
De telles optimisations sont-elles nécessaires?
Vous ne savez jamais à quoi ressemblera le code après que le compilateur contienne tout ce qu'il peut et fait un pliage constant, une copie de propagation, un CSE, etc. - une image complètement différente s'ouvrira pour lui. LLVM IR et .NET IL ne sont pas liés à un langage de programmation spécifique, et vous ne pouvez pas être sûr qu'un PL spécifique / nouveau peut se traduire efficacement en IR. Eh bien, pourquoi en parler si vous pouvez tester les performances d'InstCombine on et off sur une application spécifique ;-). Il est peu probable que ce soit une différence impressionnante, mais qui sait.
Et C #?
Comme je l'ai dit, les optimisations des expressions que nous avons examinées sont très probablement absentes en C #. Mais quand je dis C #, je veux dire que le runtime le plus populaire est CoreCLR et RyuJIT. Mais en plus de CoreCLR, il existe d'autres environnements d'exécution, y compris ceux utilisant LLVM comme backend: Mono (voir mon tweet ), Unity Burst, IL2CPP (via clang) et LILLC - ici, vous pouvez comparer en toute sécurité les résultats C ++ avec clang. Les gars d'Unity réécrivent même le code C ++ interne en C # sans aucune perte de performances, preuve !
Voici quelques pipettes d'optimisation qui peuvent être trouvées dans le fichier morph.cpp dans le code source morph.cpp des commentaires (il y en a clairement un peu plus):
*(&X) => X X % 1 => 0 X / 1 => X X % Y => X - (X / Y) * Y X ^ -1 => ~x X >= 1 => X > 0 X < 1 => X <= 0 X + 1 == C2 => X == C2 - C1 ((X + C1) + C2) => (X + (C1 + C2)) ((X + C1) + (Y + C2)) => ((X + Y) + (C1 + C2))
Un peu plus peut être trouvé dans lowering.cpp (bas niveau), mais en général RyuJIT perd évidemment ici aux compilateurs C ++. RyuJIT a des priorités légèrement différentes - avant l'avènement de la compilation par niveaux, il devait fournir une vitesse de compilation acceptable, ce qu'il fait très bien contrairement aux compilateurs C ++ (rappelez-vous de la passe InstCombine de 30 lignes dans LLVM et lisez l'intéressant article en général " "Lamentations C ++ modernes" ) et il est beaucoup plus utile de développer des optimisations dans le domaine de la dévirtualisation des appels, l'élimination de la boxe et des allocations (la même allocation de pile d'objets ) - tout cela, évidemment, est beaucoup plus important que de minimiser la division du sinus par le cosinus en tangente.
Peut-être avec l'avènement de la compilation par niveaux, avec le temps, de nombreuses nouvelles optimisations ne seront pas essentielles au temps de compilation pour le niveau 1 ou même le niveau 2. Peut-être même avec votre Add-in API et DSL - vous venez de lire cet article, Prathamesh Kulkarni y a ajouté l'optimisation d'expression dans GCC en quelques lignes DSL:
(simplify (plus (mult (SIN @0) (SIN @0)) (mult (COS @0) (COS @0))) (if (flag_unsafe_math_optimizations)1. { build_one_cst (TREE_TYPE (@0))
pour cette expression d'un manuel de mathématiques ;-):
cos^2(X) + sin^2(X) equals to 1
Liens utiles
- "Orientations futures pour l'optimisation des compilateurs" , Nuno P. Lopes et John Regehr
- "Comment LLVM optimise une fonction" , John Regehr
- "L'habileté surprenante des compilateurs modernes" , Daniel Lemire
- "Ajout de l'optimisation des judas à GCC" , Prathamesh Kulkarni
- "1. C ++, C # et Unity" , Lucas Meijer
- "Modern" C ++ Lamentations " , Aras Pranckevičius
- "Optimisations de judas correctes avec Vive" , Nuno P. Lopes, David Menendez, Santosh Nagarakatte et John Regehr