Présentation
L'un des premiers radiotélescopes construits par l'American Grotto Reber en 1937. Le radiotélescope était un miroir en étain d'un diamètre de 9,5 m monté sur un cadre en bois:

En 1944, Reber avait compilé la première carte de la distribution des ondes radio spatiales dans la région de la Voie lactée.
Le développement de la radioastronomie a entraîné un certain nombre de découvertes: en 1946, une émission radio de la constellation du Cygne a été découverte, en 1951 - rayonnement extragalactique, en 1963 - quasars, et en 1965 un rayonnement de fond relique à une longueur d'onde de 7,5 cm a été découvert.
En 1963, un radiotélescope unique de 300 mètres a été construit à Arecibo (Porto Rico). Il s'agit d'un bol immobile avec un irradiateur mobile, construit dans une fente naturelle du terrain.

Les radiotélescopes simples ont une petite résolution angulaire, qui est déterminée par la formule:
T h e t a = f r a c l a m b d a d où
l a m b d a - longueur d'onde
d - diamètre du radiotélescope.
Evidemment, pour améliorer la résolution, il est nécessaire d'augmenter le diamètre de l'antenne, ce qui est physiquement une tâche difficile. Il a été possible de le résoudre avec l'avènement des interféromètres radio.
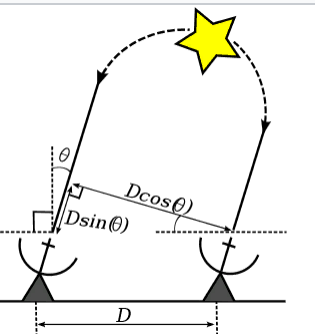
Le front d'une onde électromagnétique émise par une étoile éloignée près de la Terre peut être considéré comme plat. Dans le cas de l'interféromètre le plus simple, composé de deux antennes, la différence de trajectoire des rayons arrivant sur ces deux antennes sera égale à:
D e l t a = D c d o t s i n ( T h e t a ) ,
où:
D e l t a - la différence de trajectoire des rayons;
D - distance entre antennes;
T h e t un - l'angle entre la direction d'arrivée des rayons et la normale à la ligne sur laquelle les antennes sont situées.
À
T h e t a = 0 les ondes arrivant aux deux antennes sont additionnées en phase. En antiphase, les ondes apparaîtront pour la première fois avec:
Delta= frac lambda2, Theta=arcsin frac lambda2D ,
où:
lambda - longueur d'onde.
Le prochain maximum sera à
Delta= lambda, minimum à
Delta= frac3 lambda2 etc. Un diagramme de rayonnement à plusieurs pétales (DN) est obtenu, dont la largeur du lobe principal
lambda<<D est égal à
lambda/D . La largeur du lobe principal détermine la résolution angulaire maximale du radio-interféromètre, elle est approximativement égale à la largeur du lobe.
L'interférométrie radio à base ultra longue (VLBI) est un type d'interférométrie utilisé en radioastronomie dans lequel les éléments récepteurs de l'interféromètre (télescopes) ne sont situés pas plus près qu'à des distances continentales les unes des autres.
La méthode VLBI vous permet de combiner les observations faites par plusieurs télescopes, et ainsi de simuler un télescope dont les dimensions sont égales à la distance maximale entre les télescopes d'origine. La résolution angulaire du VLBI est des dizaines de milliers de fois supérieure à la résolution des meilleurs instruments optiques.
L'état actuel des réseaux VLBI
Aujourd'hui, plusieurs réseaux VLBI écoutent l'espace:
- European –EVN (European VLBI Network), composé de plus de 20 radiotélescopes;
- American –VLBA (Very Long Baseline Array), qui comprend dix télescopes d'un diamètre de 25 mètres chacun;
- Japonais - JVN (Japanese VLBI Network) se compose de dix antennes situées au Japon, dont quatre antennes astrométriques (projet VERA - VLBI Exploration of Radio Astrometry);
- Australie - LBA (Long Baseline Array);
- Chinois - CVN (réseau chinois VLBI), composé de quatre antennes;
- Corée du Sud - KVN (Korean VLBI Network), qui comprend trois radiotélescopes de 21 mètres;
- Le Russe - basé sur le complexe radio-interférométrique permanent - "Kvazar-KVO" avec des radiotélescopes d'un diamètre de 32 m, équipés de cryoradiomètres très sensibles dans la gamme de longueurs d'onde de 1,35 cm à 21 cm. La longueur des bases - le diamètre effectif du "miroir" synthétisé - est d'environ 4400 km dans la direction est-ouest (voir photo).
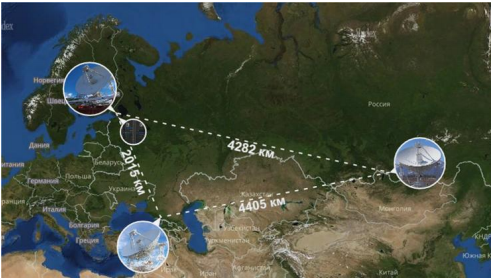
Dans le complexe VLBI «Kvazar-KVO», les étalons d'hydrogène sont utilisés comme source de fréquence de référence pour toutes les transformations de fréquence, qui utilisent la transition entre les niveaux de la structure hyperfin de l'état fondamental d'un atome d'hydrogène avec une fréquence de 1420,405 MHz, correspondant à 21 cm en radioastronomie.
Tâches résolues au moyen du VLBI
- Astrophysique Des images radio d'objets spatiaux naturels (quasars et autres objets) sont en cours de construction avec une résolution de dixièmes et centièmes de mas (millisecondes d'arc).
- Études astrométriques. Construction de systèmes à temps coordonné. Les objets de recherche sont des sources radio de très petites tailles angulaires, y compris des sources radio quasistellaires et les noyaux de radio galaxies, qui, en raison de leur grande distance, sont des objets presque idéaux pour créer un réseau d'objets stationnaires de support.
- Recherche sur la mécanique céleste et la dynamique du système solaire, navigation spatiale. L'installation d'une balise sur les surfaces des planètes et le suivi des balises des stations automatiques interplanétaires permettent d'utiliser la méthode VLBI pour étudier des paramètres tels que le mouvement orbital de la planète, la direction des axes de rotation et leur précession, la dynamique du système planète-satellite. Pour la Lune, le problème très important de déterminer la libration physique et de déterminer la dynamique des systèmes Lune-Terre est également résolu.
Navigation dans l'espace avec VLBI
- Surveillance des mouvements des astronautes sur la surface lunaire en 1971. Ils se sont déplacés avec l'aide du rover lunaire Rover. La précision de la détermination de sa position par rapport au module lunaire atteignait 20 cm et dépendait principalement de la libration de la lune (Libration - oscillations périodiques en forme de pendule de la lune par rapport à son centre de masse);
- Aide à la navigation pour la livraison et la décharge des sondes d'aérostat des véhicules volants dans l'atmosphère de Vénus (projet VEGA). La distance à Vénus est de plus de 100 millions de km, la puissance de l'émetteur n'est que de 1 Watt. Les lancements de VEGA-1/2 ont eu lieu en décembre 1984. Des ballons ont été largués dans l'atmosphère de Vénus les 11 et 15 juin 1985. L'observation a été effectuée pendant 46 heures.
Schéma structurel d'un réseau VLBI simplifié
Sur la base d'un véritable réseau VLBI, à l'aide du logiciel Python, nous modélisons un système VLBI simplifié sous la forme de modèles distincts pour chaque unité ou processus. Cet ensemble de modèles sera suffisant pour observer les processus de base. Le schéma structurel d'un réseau VLBI simplifié est présenté dans la figure:
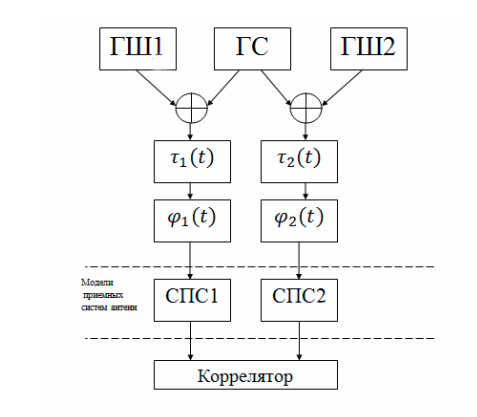
Le système comprend les composants suivants:
- générateur utile signal modulé en phase (HS);
- générateurs de bruit (GSh1, GSh2). Le système dispose de deux radiotélescopes (antennes de réception) qui ont leur propre bruit. De plus, il y a des bruits de l'atmosphère et d'autres sources naturelles et artificielles d'émission radio;
- une unité de retard temporel simulant un retard temporel variant linéairement en raison de la rotation de la Terre;
- déphaseur simulant l'effet Doppler;
- système de conversion de signal (SPS), composé d'un oscillateur local, pour transférer le signal vers le bas en fréquence, et d'un filtre passe-bande;
- Corrélateur FX.
Le circuit corrélateur est illustré dans la figure suivante:
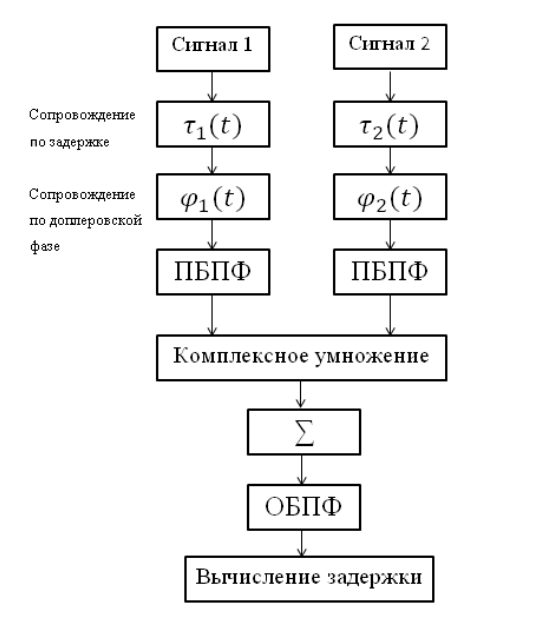
Le circuit corrélateur donné, qui comprend les blocs suivants:
- transformée de Fourier rapide directe (PBPF) et transformée de Fourier inverse (OBPF);
- compenser le retard introduit précédemment;
- effet Doppler compensateur;
- multiplication complexe de deux spectres;
- additionnant les implémentations accumulées.
Modèle de signal de navigation
Les signaux de navigation des engins spatiaux des systèmes de navigation par satellite, tels que le GPS et le GLONASS, sont les plus pratiques pour les mesures VLBI. Un certain nombre d'exigences sont imposées aux signaux de navigation:
- vous permettent de bien définir la pseudodistance;
- transmettre des informations sur la position du système de navigation;
- se distinguer des signaux des autres NS;
- N'interférez pas avec d'autres systèmes radio;
- pas besoin d'équipement complexe pour recevoir et transmettre.
Dans une mesure suffisante, ils sont satisfaits d'un signal à modulation de phase binaire (à deux positions) - BPSK (touche de décalage de phase binaire), qui dans la littérature russe est désigné comme FM-2. Cette modulation modifie la phase de l'oscillation de la porteuse par π, qui peut être représenté comme:
S(t)=A cdotG(t) cdotcos(2 pift),où G (t) est la fonction de modulation.
Pour mettre en œuvre la modulation de phase, deux générateurs peuvent être utilisés, chacun formant la même fréquence, mais avec une phase initiale différente. La fonction de modulation vous permet d'étendre le spectre du signal et de mesurer avec précision la pseudo-distance (la distance entre le satellite et le récepteur, calculée par le temps de propagation du signal sans correction de la différence entre l'horloge du satellite et le récepteur).
Voici une liste expliquant les principes de base du BPSK:
Annoncefrom scipy import* from pylab import* import numpy as np import scaleogram as scg f = 2;
Nous obtenons:
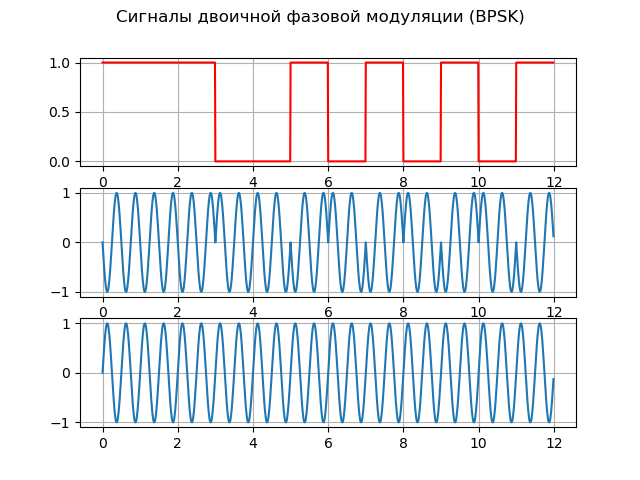
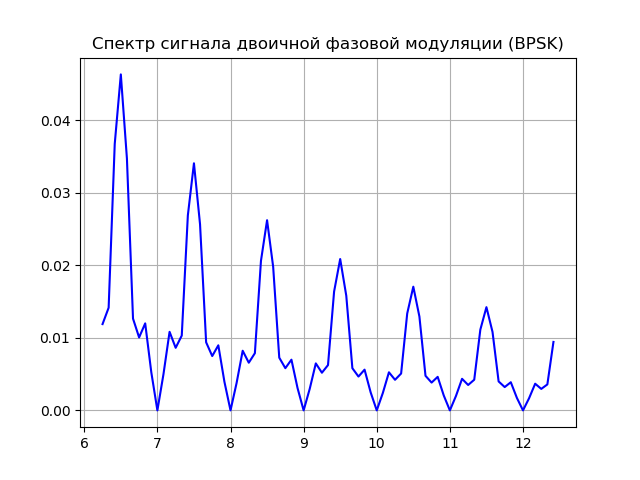
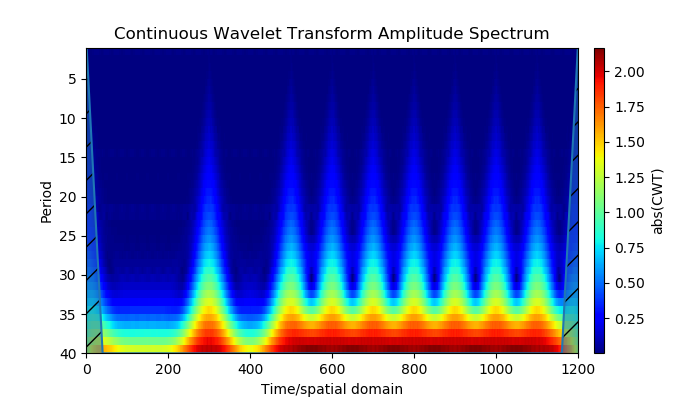
Modèle source
Le signal harmonique de navigation modulé en phase provenant d'un satellite ou d'un engin spatial a la forme:
x=a(2 pifct+ sumsncos(2 pifnt)),où est la fréquence porteuse
fc=8,4 GHz
Le signal a plusieurs paramètres contrôlés: l'amplitude de la nième oscillation modulante
sn, sa fréquence
fc et l'amplitude de l'oscillation de la porteuse a.
Pour obtenir une fonction de corrélation dans laquelle ses lobes latéraux sont supprimés autant que possible et le pic de corrélation le plus étroit est atteint, nous allons faire varier les valeurs de fréquence en utilisant les valeurs de 2, 4, 8 et 16 MHz, et l'indice de modulation dans la plage de 0 à 2π par incréments de π. Permettez-moi de vous donner une liste du programme pour une telle recherche de paramètres d'une fonction modulée en phase pour le résultat final:
Nous obtenons:
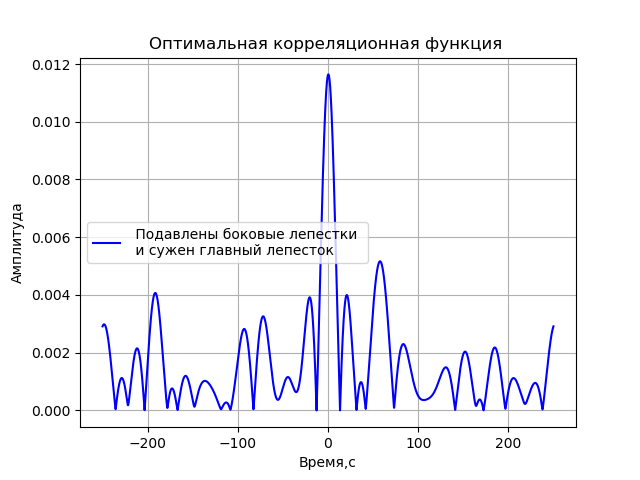
La fonction résultante a la forme:
x=cos(2 pifct+2 picos(2 pi106t)+2 picos(2 pi108t)+4 picos(2 pi1016t)).(1)De plus, cette fonction sera utilisée pour simuler VLBI.
Modèle d'un générateur de bruit simulant les interférences reçues avec un signal provenant de l'espace et de l'atmosphère terrestre
La fonction (1) du signal de navigation modulé en phase peut être appliquée aux deux canaux du radio-interféromètre, mais il est nécessaire de prendre en compte le retard du signal dans le deuxième canal et le bruit dans les deux canaux, comme indiqué dans la liste suivante:
Nous obtenons:
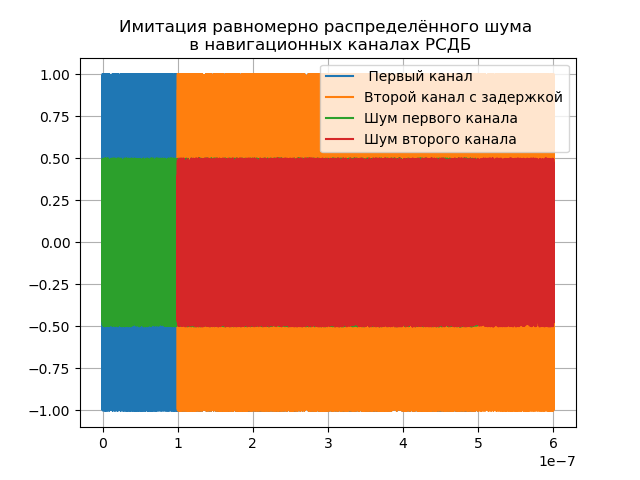
Le délai de retard = 1e-7 est défini pour la démonstration, en réalité il dépend de la base et peut atteindre quatre unités ou plus.
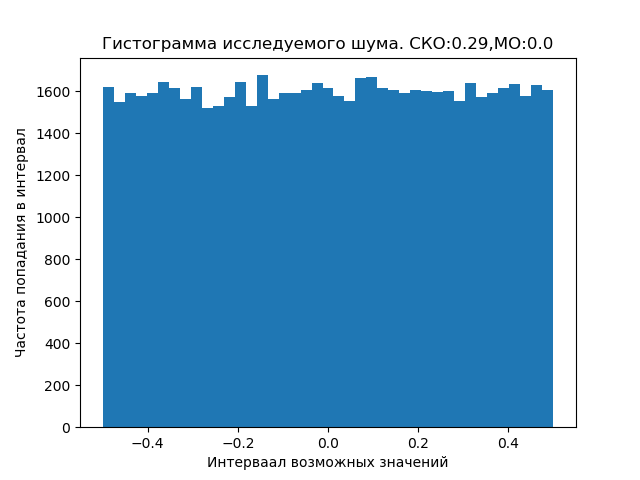
Les bruits à la fois cosmiques et proches de la Terre peuvent être distribués selon une loi différente de l'uniforme donné, ce qui nécessite des études spéciales.
Modélisation de l'effet Doppler
En raison du fait que la Terre a une forme arrondie et tourne autour de son axe, les signaux de l'espace arrivent aux antennes avec différents retards. Pour cette raison, il est nécessaire de décaler les signaux dans le temps et de prendre en compte la fréquence Doppler. On considérera approximativement que le retard varie selon une loi linéaire:
taux(t)=ax+bxt,(2)où
ax=1..3 cdot10−3 ms, et
bx=1..3 cdot10−6 ms La phase Doppler se trouve dérivée du retard:
fdx= fracd tau(t)dt=bx,(3)Le signal reçu doit ressembler à:
hatx=x(t− taux)ej2 pifdxt,où x (t) est le signal rayonné de l'engin spatial.
Une démonstration de l'effet Doppler est présentée dans la liste suivante:
Nous obtenons:
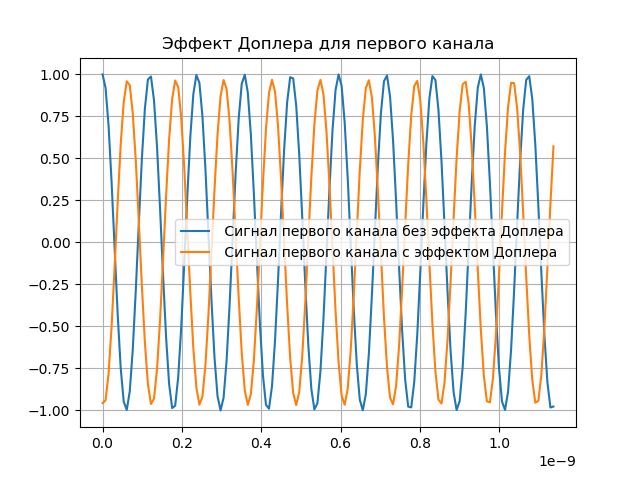
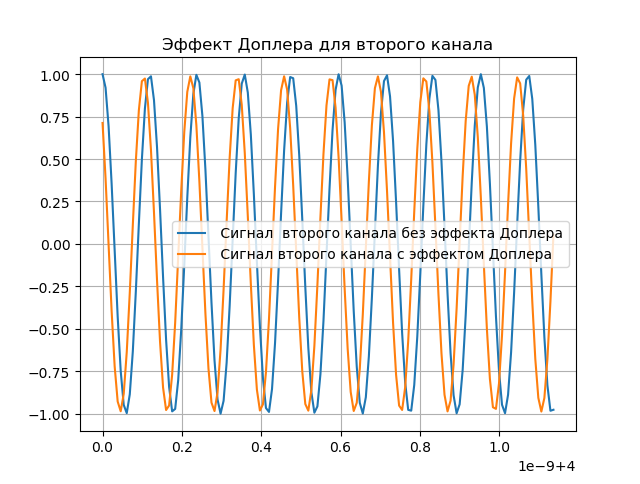
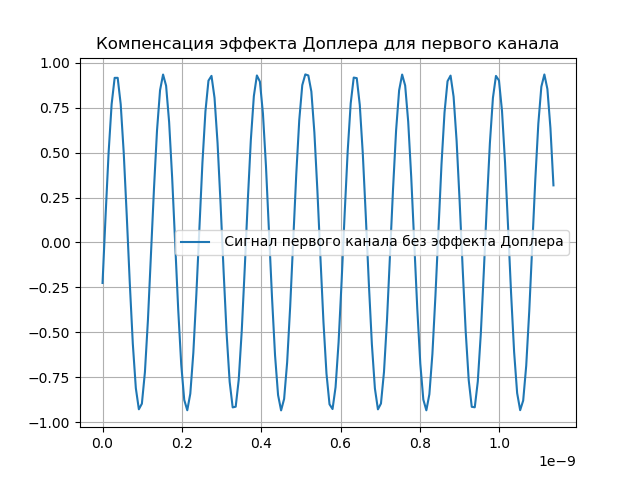
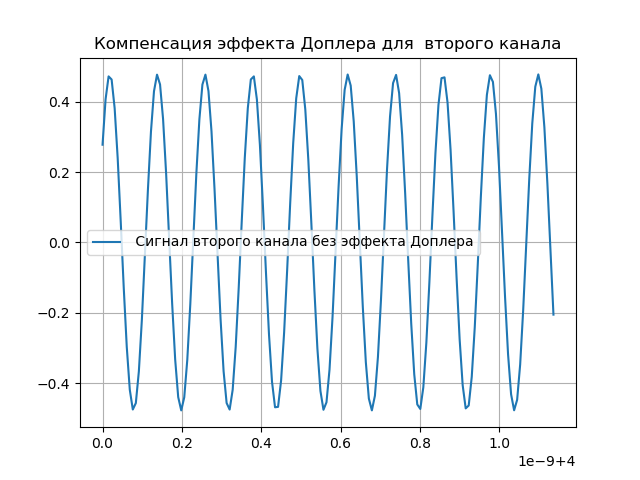
Modélisation de la compensation Doppler
De toute évidence, les modifications apportées au signal doivent être compensées. À cette fin, le système contient un support pour le retard et la phase Doppler. Après le passage du signal dans le système d'enregistrement, un délai est introduit:
tauex(t)=ax+bext,(4)Il considérera que le retard est calculé avec une certaine précision, telle que
gauche|aex−ax droite|<30 ns
gauche|bex−bx droite|<10 ns, c'est-à-dire Ce sera un peu différent de ce qu'il a fait plus tôt. Il est clair que le retard est introduit avec le signe opposé à celui introduit précédemment.
Le signal reçu ressemblera à:
hatx= tildex(t+ tauex)e−j2 pifdet.(5)La compensation de l'effet Doppler est indiquée dans la liste suivante:
Nous obtenons:
Simulation hétérodyne du signal
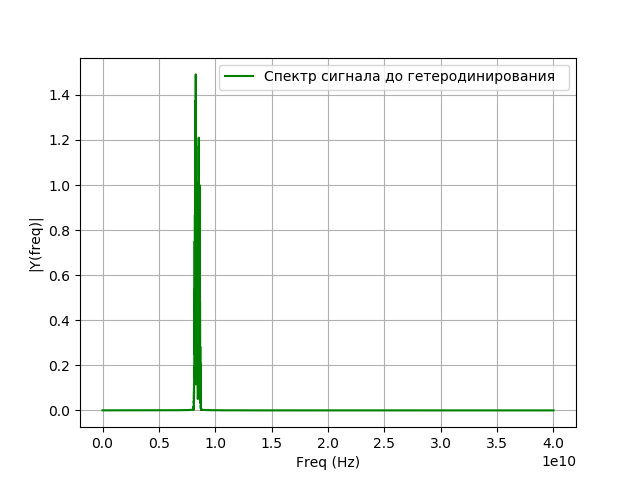
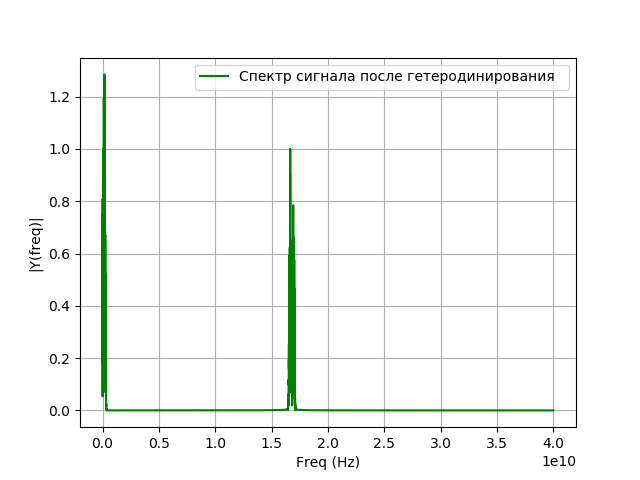
Après l'entrée du signal dans le système d'enregistrement, une conversion de fréquence se produit, également appelée hétérodynage. Il s'agit d'une transformation non linéaire dans laquelle des signaux de deux fréquences différentes
f1 et
f2 le signal de fréquence de différence est mis en évidence -
f= left|f1−f2 droite.| La fréquence du signal de l'oscillateur local sera égale à la différence entre la fréquence du signal étudié et la fréquence que vous souhaitez obtenir après le transfert. L'hétérodynage est effectué à l'aide d'un générateur auxiliaire d'oscillations harmoniques - un oscillateur local et un élément non linéaire. Mathématiquement, l'hétérodynage est la multiplication d'un signal par un exposant:
xg= hatxej2 pifgt,(6)où
fg - signal d'oscillateur local.
Programme d'hétérodynage:
Nous obtenons:
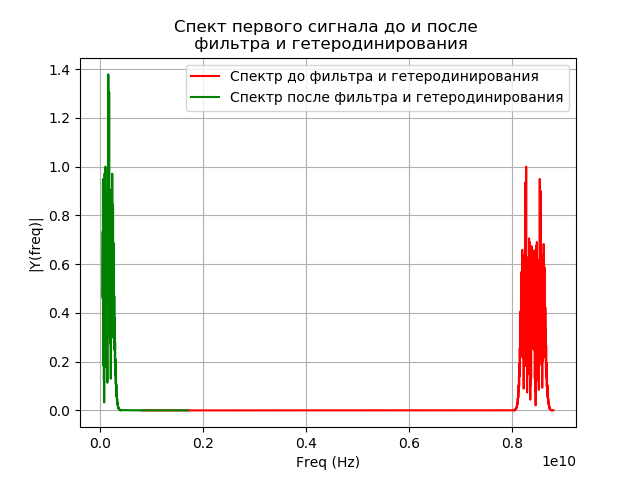
Modélisation du filtrage du signal après hétérodynage
Après hétérodynage, le signal entre dans le filtre passe-bande. Bande passante du filtre (PP)
fpass=32 MHz La réponse impulsionnelle du filtre est calculée par la méthode de la fenêtre en utilisant la fonction de bibliothèque signal.firwin. Pour obtenir un signal à la sortie du filtre, la convolution du filtre et du signal dans le domaine temporel est effectuée. L'intégrale de convolution pour notre cas prend la forme:
checkx(t)= int+ infty− inftyxg(t)h(t−t′)dt,(7)où h (t) est la réponse impulsionnelle du filtre.
La convolution est trouvée en utilisant la fonction de bibliothèque signal.convolve. Le signal enregistré, prenant en compte l'hétérodynage et le filtrage, se présente sous la forme d'une formule
checkx(t)=( hatx(t)e−j2 pifgt)∗hoù la convolution est indiquée par *.
Programme de modélisation de la filtration:
Nous obtenons:
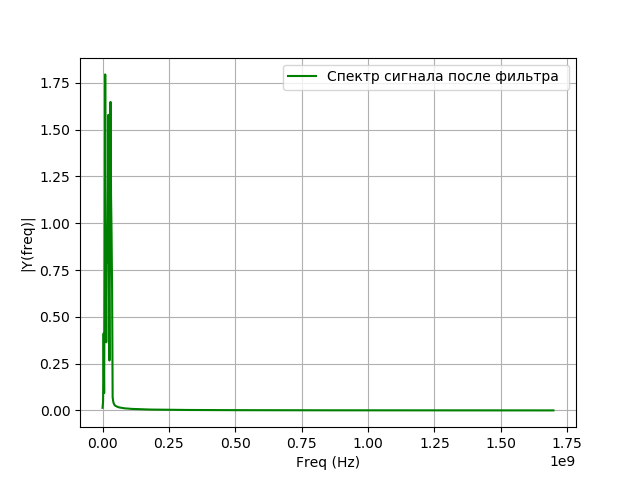
Les convertisseurs de signaux numériques pour VLBI utilisent principalement des filtres à réponse impulsionnelle finie (FIR), car ils présentent un certain nombre d'avantages par rapport aux filtres à réponse impulsionnelle infinie (IIR):
- Les filtres FIR peuvent avoir une réponse de phase strictement linéaire dans le cas d'une symétrie de réponse impulsionnelle (IM). Cela signifie qu'en utilisant un tel filtre, les distorsions de phase peuvent être évitées, ce qui est particulièrement important pour la radio-interférométrie. Les filtres à réponse impulsionnelle infinie (IIR) n'ont pas les propriétés de symétrie de THEM et ne peuvent pas avoir une réponse de phase linéaire.
- Les filtres FIR sont non récursifs, ce qui signifie qu'ils sont toujours stables. La stabilité des filtres IIR ne peut pas toujours être garantie.
- Les conséquences pratiques de l'utilisation d'un nombre limité de bits pour implémenter des filtres sont significativement moins importantes pour les filtres FIR.
Dans la liste ci-dessus, le modèle du filtre passe-bande FIR est mis en œuvre en utilisant la méthode de la fenêtre, l'ordre du filtre a été sélectionné de sorte que la forme de la réponse en fréquence du filtre était proche de rectangulaire. Le nombre de coefficients du filtre simulé est n = 100001, c'est-à-dire que l'ordre du filtre est P = 100000.
Programme de construction de la réponse en fréquence et de la réponse en phase du filtre FIR obtenu:
Nous obtenons:

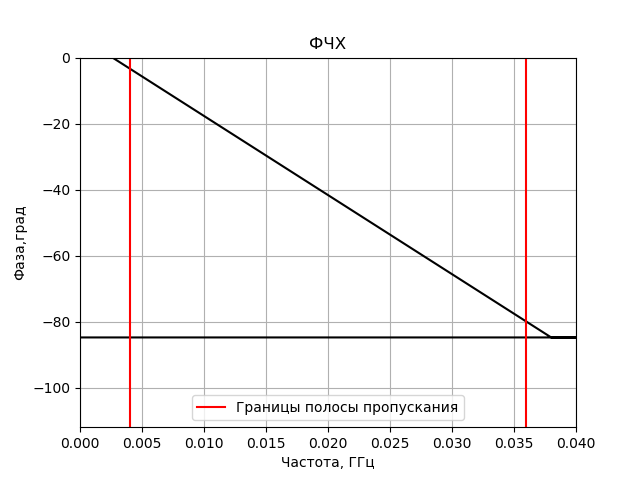
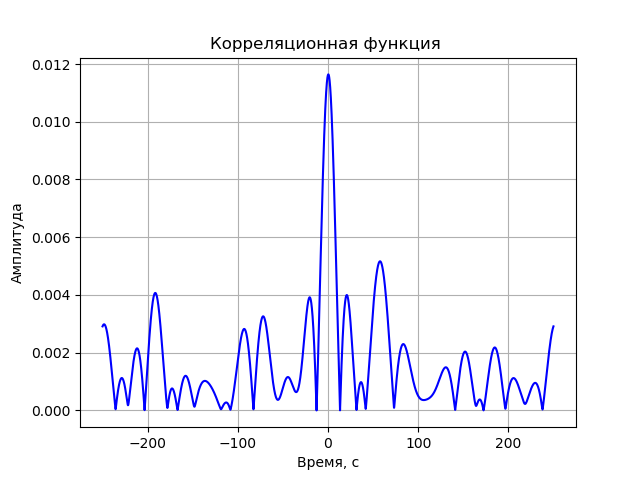
Modèle de corrélateur FX
Ensuite, chaque signal subit une transformée de Fourier rapide (FFT). FFT est implémenté à l'aide de la fonction de bibliothèque fft de scipy.fftpack. Les spectres résultants sont des conjugués complexes multipliés:
S(j omega)=S1(j omega)∗S2(j omega)=(a1+jb1)∗(a2−jb2)=a1a2+b1b2+j(b1a2−a1b2)La dernière action est l'inverse de la FFT. Comme l'amplitude de la fonction de corrélation est intéressante, le signal résultant doit être converti par la formule:
A= sqrtre2+im2Le programme de la fonction de corrélation sans prendre en compte les distorsions du système d'enregistrement:
Nous obtenons:
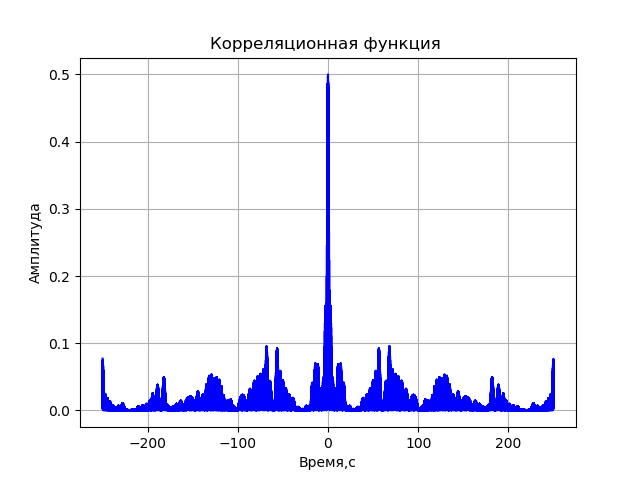
Liste complète du modèle informatique du VLBI:
Nous obtenons:
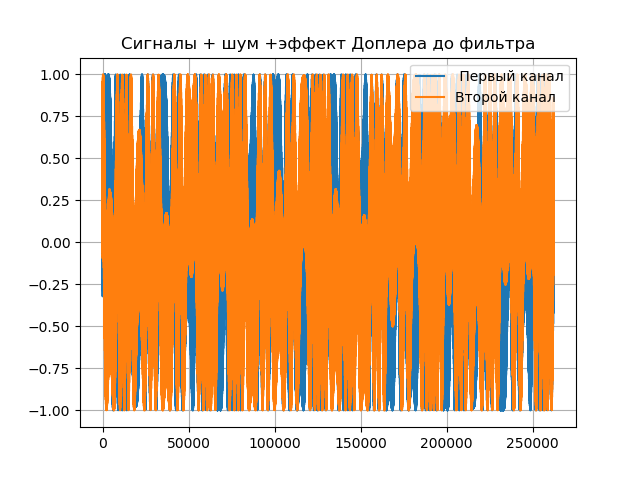

Conclusions
- Une brève histoire du développement de la radioastronomie est donnée.
- L'état actuel des réseaux VLBI est analysé.
- Les problèmes résolus au moyen des réseaux VLBI sont considérés.
- Les outils Python ont construit un modèle de signaux de navigation avec modulation de phase binaire (à deux positions) - BPSK (touche de décalage de phase binaire). Le modèle utilise l'analyse en ondelettes de la modulation de phase.
- Un modèle de sources de signaux a été obtenu, qui permet de déterminer les paramètres de modulation qui fournissent la fonction de corrélation optimale selon le critère de suppression des lobes latéraux et l'amplitude maximale du lobe central.
- Un modèle de réseau VLBI simplifié est obtenu, prenant en compte le bruit et l'effet Doppler. Les caractéristiques du filtrage utilisant un filtre à réponse impulsionnelle finie sont considérées.
- Après un bref résumé de la théorie, tous les modèles sont équipés de programmes de démonstration qui vous permettent de suivre l'influence des paramètres du modèle.