La segmentation manuelle des poumons prend environ 10 minutes et nécessite une certaine habileté pour obtenir le même résultat de haute qualité qu'avec la segmentation automatique. La segmentation automatique prend environ 15 secondes.
J'ai supposé que sans réseau neuronal, il serait possible d'obtenir une précision ne dépassant pas 70%. J'ai également suggéré que les opérations morphologiques préparent simplement une image pour des algorithmes plus complexes. Mais à la suite du traitement de ces au moins quelques 40 échantillons tomographiques disponibles, l'algorithme a sélectionné les poumons sans erreur, et après le test dans les cinq premiers cas, l'algorithme n'a pas subi de changements significatifs et dès la première application, il a fonctionné correctement sur les 35 études restantes sans changement. paramètres.
Les réseaux de neurones ont également un inconvénient - pour leur entraînement, vous avez besoin de centaines d'échantillons d'entraînement des poumons, qui devront être étiquetés manuellement.
Table des matières
La structure du système respiratoire
Le système respiratoire comprend les voies respiratoires et les poumons. Allouez les voies respiratoires supérieures et inférieures. Le point de séparation entre les voies respiratoires inférieures et supérieures est le point d'intersection des canaux alimentaire et respiratoire. Tout au-dessus du larynx est la partie supérieure et le reste est plus bas.
Nous listons les organes respiratoires:
Cavité nasale : - nez, sinus maxillaires, etc.
Le pharynx est le canal par lequel la nourriture et l'air voyagent.
Larynx - responsable de la formation de la voix. Situé au niveau des vertèbres cervicales C4-C6.
Trachée - un tube reliant le larynx et les bronches.
Les bronches sont les canaux respiratoires, dont la plupart sont situés à l'intérieur des poumons.
Les poumons sont le principal organe respiratoire.

Échelle de Hounsfield
Godfrey Hounsfield est un ingénieur électricien britannique qui, avec le théoricien américain Allan Cormack, a développé la tomodensitométrie, pour laquelle il a reçu le prix Nobel en 1979.

Échelle de Hounsfield - Une échelle quantitative de densité de rayons X qui est mesurée en unités de Hounsfield, notée HU.
La densité des rayons X est calculée sur la base du coefficient d'atténuation de la substance, c'est-à-dire du degré de diminution de la puissance de rayonnement lors du passage à travers cette substance.
La densité des rayons X est calculée par la formule:
$$ afficher $$ {μ_ {X} -μ_ {eau} \ sur μ_ {eau} -μ_ {air}} \ fois 1000 $$ afficher $$
où μX,μeau,μair - coefficients d'atténuation linéaire pour la substance mesurée, l'eau et l'air.
La densité de rayons X est négative car une densité de rayons X nulle correspond à l'eau. Cela signifie que toutes les substances à travers lesquelles les ondes radiographiques passent avec une diminution de la puissance de rayonnement plus faible que par l'eau (par exemple, les tissus pulmonaires, l'air) auront une densité de rayons X négative.
Voici les densités de rayons X approximatives pour divers tissus:
- Air: -1000 HU.
- Organes respiratoires: -950 à -300 HU.
- Sang (sans contraste vasculaire): 0 à 100 HU.
- Os: 100 à 1000 HU.

Liens Wikipédia: échelle de Hounsfield , Godfrey Hounsfield , coefficient d'atténuation .
Morphologie mathématique
La place principale parmi les algorithmes sélectionnés dans cet article est occupée par les opérations morphologiques.
Dans le domaine de la vision par ordinateur, les opérations morphologiques appellent un groupe d'algorithmes pour transformer la forme des objets. Le plus souvent, les opérations morphologiques sont appliquées aux images binarisées, où les voxels des objets correspondent aux unités et le vide aux zéros.
Les principales opérations morphologiques comprennent:
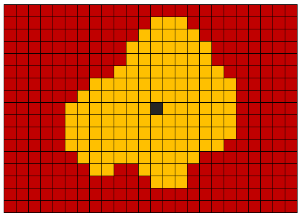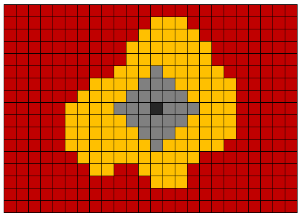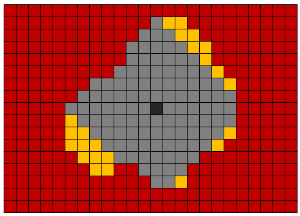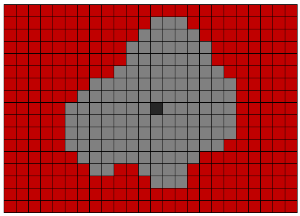
Dilatation morphologique (dilatation, expansion) - ajout de nouveaux voxels à tous les voxels de bord d'objets. Autrement dit, le long de tous les voxels limites, un passage est fait avec un noyau avec une forme donnée (boule, cube, croix, etc.). Cette opération est souvent utilisée pour connecter de nombreux objets adjacents en un seul objet.
Érosion morphologique (érosion, érosion) - la destruction de tous les voxels se trouvant à la frontière des objets. Cette opération est l'opposé de la dilatation. Cette opération est utile pour éliminer le bruit sous la forme de nombreux petits objets interconnectés. Cependant, cette méthode d'élimination du bruit ne doit être utilisée que si l'objet segmenté a une épaisseur nettement supérieure au rayon d'érosion.
La fermeture morphologique est une dilatation suivie d'une érosion. Il est utilisé pour fermer les ouvertures à l'intérieur des objets et pour combiner des objets adjacents.
L'ouverture morphologique (ouverture) est l'érosion suivie d'une dilatation. Il est utilisé pour supprimer les petits objets de bruit et pour diviser les objets en plusieurs objets.


Algorithme Lee et compression RLE
Pour isoler des objets dans un volume de voxel binarisé, l'algorithme Lee est utilisé. Cet algorithme a été inventé à l'origine pour trouver le chemin le plus court. Mais nous l'utilisons pour sélectionner et déplacer des objets d'un tableau tridimensionnel de voxels à un autre. Son essence est un mouvement parallèle dans toutes les directions possibles à partir du point de départ. Pour le cas tridimensionnel, 26 ou 6 directions de mouvement à partir d'un voxel donné sont possibles (si le voxel n'est pas situé au bord de l'image).
Pour optimiser la vitesse, nous avons utilisé l'algorithme d'encodage de longueur d'exécution. Son essence réside dans le fait que les séquences de uns et de zéros sont remplacées par un chiffre égal au nombre d'éléments de la séquence. Par exemple, la chaîne «00110111» peut être remplacée par: «2; 2; 1; 3». Cela réduit le nombre d'accès à la mémoire.

Liens Wikipedia: algorithme Lee, algorithme RLE .
Conversion du volume de base du seuil
À l'aide d'un tomographe, des données sur la densité des rayons X à chaque point dans l'espace ont été obtenues. Les voxels aériens ont une densité de rayons X allant de -1100 à -900 HU, et les voxels des organes respiratoires de -900 à -300 HU. Par conséquent, nous pouvons éliminer tous les voxels en excès ayant une densité de rayons X supérieure à -300 HU. En conséquence, nous obtenons un volume de voxel binarisé contenant uniquement des organes respiratoires et de l'air.
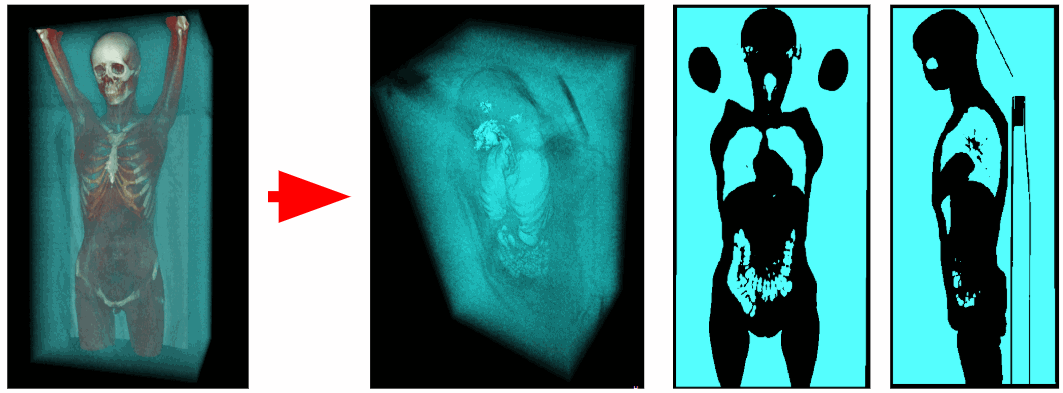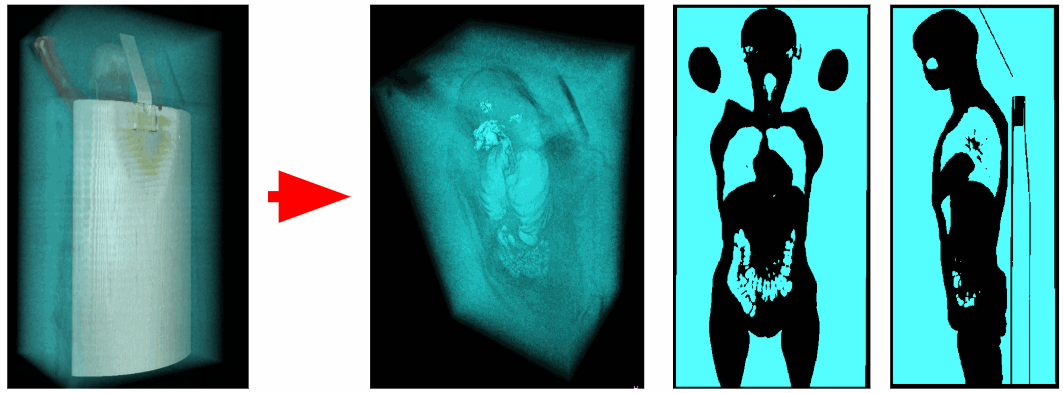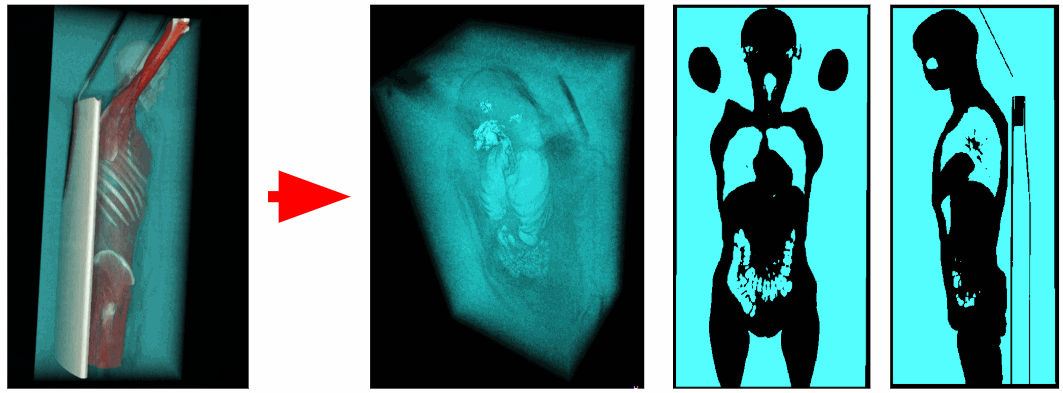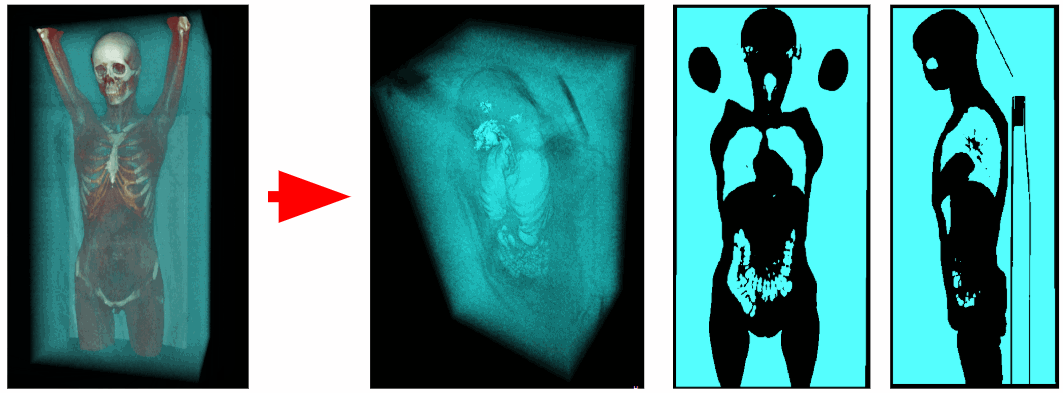
Coupure d'air externe
Pour isoler l'air interne du corps, nous allons supprimer tous les objets adjacents aux coins de la scène voxel. Ainsi, nous nous débarrassons de l'air extérieur.

Cependant, dans tous les cas, l'air à l'intérieur de la table du tomographe ne sera pas éliminé, car il peut ne pas avoir de connexion avec les coins de la scène.

Par conséquent, nous scannerons non seulement les coins, mais également tous les voxels se trouvant sur l'un des plans limites de la scène. Mais en conséquence, pour une raison quelconque, les poumons eux-mêmes sont également partis. Il s'avère que la trachée avait également un lien avec le plan supérieur de la scène.
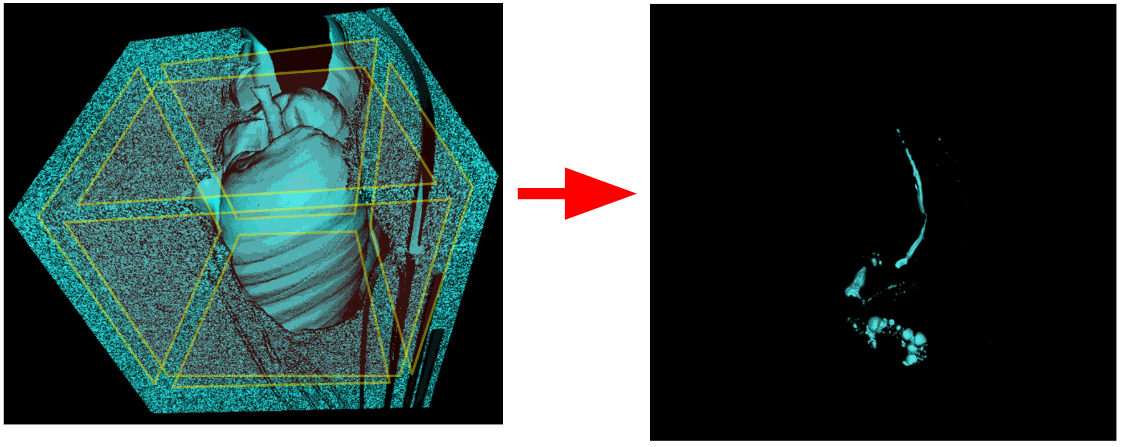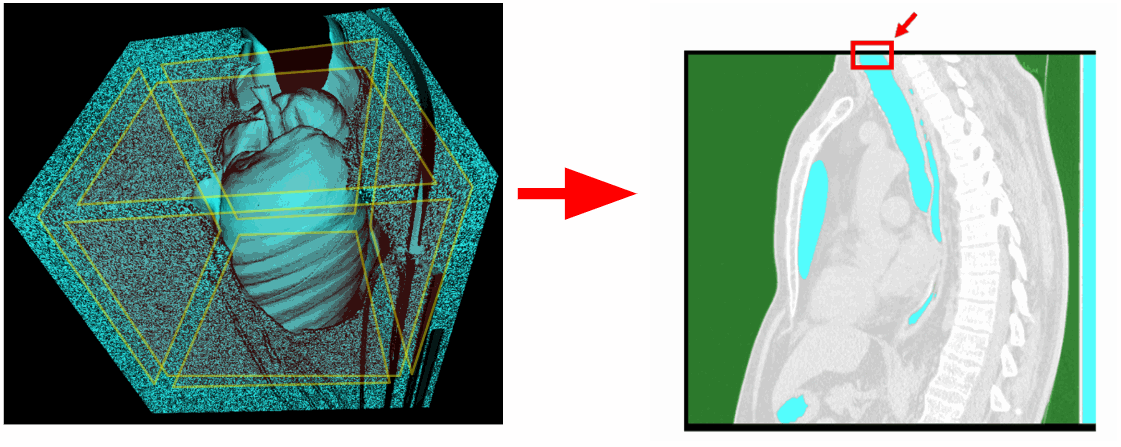
Il est nécessaire d'exclure le plan supérieur de la zone de balayage. Il existe également des études dans lesquelles les poumons n'ont pas été complètement capturés et le plan inférieur est associé aux poumons. Ainsi, si vous le souhaitez, le plan inférieur peut également être exclu.

Mais cette méthode n'agit que sur les études mammaires. Dans le cas de la capture de tout le volume du corps, une connexion entre l'air interne et externe à travers la cavité nasale apparaîtra sur l'image. Par conséquent, il est nécessaire d'appliquer une érosion morphologique pour séparer l'air interne et externe.
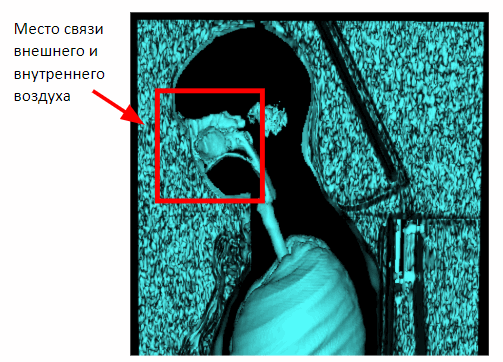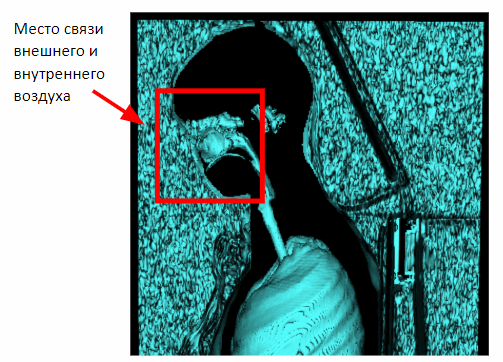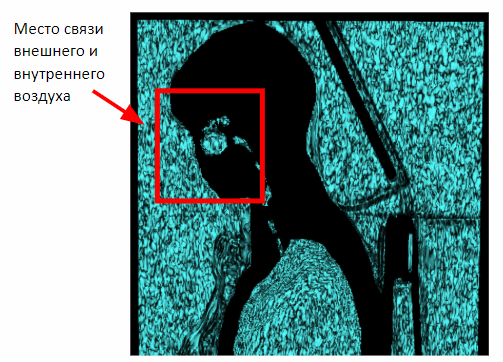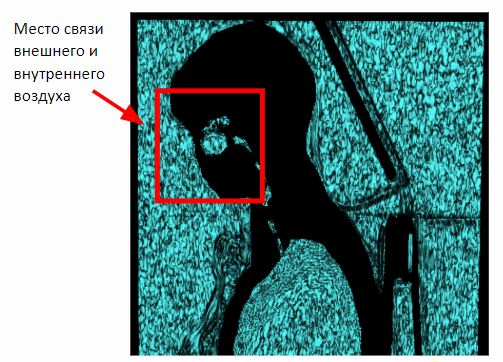
Après avoir appliqué l'érosion, nous pouvons revenir à la méthode de segmentation de l'air extérieur précédemment obtenue en fonction de la proximité des plans latéraux de la scène.

En isolant l'air extérieur, on pourrait immédiatement le retirer du volume total d'air et de poumons et obtenir l'air intérieur du corps et des poumons. Mais il y a un problème. Après l'érosion, certaines informations sur l'air extérieur ont été perdues. Pour le restaurer, nous appliquons la dilatation de l'air extérieur.

Ensuite, nous soustrayons l'air extérieur de tous les organes de l'air et des voies respiratoires et obtenons l'air intérieur et les organes respiratoires.


Mettre en surbrillance l'objet maximum en volume
Ensuite, nous sélectionnons les organes respiratoires comme le plus grand objet en volume. Les organes respiratoires sont un objet distinct. Il n'y a aucun lien entre les poumons et l'air à l'intérieur du tractus gastro-intestinal.


Il convient de noter que le choix correct du seuil de densité de rayons X à l'étape initiale de la transformation de seuil est important. Sinon, dans certains cas, il peut ne pas y avoir de connexion entre les deux poumons en raison d'une faible résolution. Par exemple, si vous considérez que les voxels des organes respiratoires ont une densité de rayons X de -500 HU ou moins, alors dans le cas ci-dessous, l'attribution des organes respiratoires comme le plus grand objet en volume entraînera une erreur, car il n'y a pas de connexion entre les deux poumons. Par conséquent, le seuil devrait être augmenté à -300 HU.

Fermeture vasculaire à l'intérieur des poumons
Pour capturer les vaisseaux à l'intérieur des poumons, nous utilisons une fermeture morphologique, c'est-à-dire une dilatation suivie d'une érosion de même rayon. La densité des rayons X des vaisseaux est d'environ -100..100 HU.

Les gros vaisseaux sanguins ne se sont pas fermés. Mais ce n'est pas nécessaire. Le but de cette opération était de détruire de nombreux petits trous à l'intérieur des poumons pour faciliter la segmentation pulmonaire.
Algorithme de segmentation respiratoire
En conséquence, nous obtenons l'algorithme de segmentation des organes respiratoires suivant:
- Conversion de seuil de volume de base par seuil <-300 HU.
- Érosion morphologique d'un rayon de 3 mm pour la séparation de l'air extérieur et intérieur.
- L'allocation de l'air extérieur sur la base de la proximité des plans latéraux limites de la scène voxel.
- Dilatation morphologique de l'air extérieur pour restaurer les informations perdues à la suite de l'érosion.
- Soustraction de l'air extérieur de tous les organes de l'air et des voies respiratoires pour obtenir l'air intérieur et les organes respiratoires.
- Mettre en surbrillance l'objet maximum en volume.
- Fermeture morphologique des vaisseaux sanguins à l'intérieur des poumons.

Implémentation de l'algorithme dans MATLAB
Méthode GetRespiratoryOrgans
Méthode GetExternalAir
Méthode GetMaxObject
Le code source peut être téléchargé ici .
Conclusion
Les articles suivants sont prévus:
- segmentation de la trachée et des bronches;
- segmentation des poumons;
- segmentation des lobes des poumons.
Des algorithmes tels que:
- transformation de distance;
- transformation du plus proche voisin (transformation du plus proche voisin, également appelée transformation d'entité);
- calcul des valeurs propres de la matrice de Hesse pour la segmentation d'objets 3D plats;
- segmentation par segmentation du bassin versant.