Nous continuons de parler de la conférence sur les statistiques et l'apprentissage automatique AISTATS 2019. Dans cet article, nous analyserons des articles sur les modèles profonds d'ensembles d'arbres, mélangerons la régularisation pour les données très rares et l'approximation efficace du temps de la validation croisée.

Algorithme de forêt profonde: une exploration des modèles profonds non-NN basés sur des modules non différenciables
Zhi-Hua Zhou (Université de Nanjing)
→ Présentation
→ Article
Implémentations - ci-dessous
Un professeur chinois a parlé de l'ensemble des arbres, que les auteurs appellent la première formation approfondie sur des modules non différenciables. Cela peut sembler une déclaration trop forte, mais ce professeur et son H-index 95 sont des conférenciers invités, ce fait nous permet de prendre la déclaration plus au sérieux. La théorie de base de Deep Forest a été développée depuis longtemps, l'article original est déjà 2017 (près de 200 citations), mais les auteurs écrivent des bibliothèques et chaque année ils améliorent l'algorithme en vitesse. Et maintenant, semble-t-il, ils ont atteint le point où cette belle théorie peut enfin être mise en pratique.
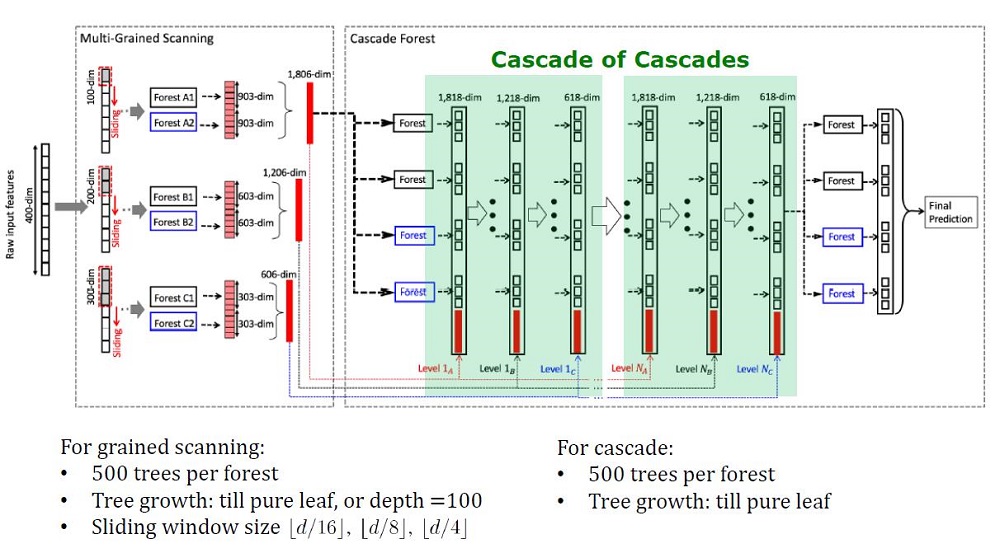
Vue générale de l'architecture Deep Forest
Contexte
Les modèles profonds, qui sont maintenant compris comme des réseaux de neurones profonds, sont utilisés pour capturer des dépendances de données complexes. De plus, il s'est avéré que l'augmentation du nombre de couches est plus efficace que l'augmentation du nombre d'unités sur chaque couche. Mais les réseaux de neurones ont leurs inconvénients:
- Il faut beaucoup de données pour ne pas se recycler,
- Il faut beaucoup de ressources informatiques pour apprendre dans un laps de temps raisonnable,
- Trop d'hyperparamètres difficiles à configurer de manière optimale
De plus, les éléments des réseaux de neurones profonds sont des modules différenciables qui ne sont pas nécessairement efficaces pour chaque tâche. Malgré la complexité des réseaux de neurones, des algorithmes conceptuellement simples, comme une forêt aléatoire, fonctionnent souvent mieux ou pas moins bien. Mais pour de tels algorithmes, vous devez concevoir manuellement des fonctionnalités, ce qui est également difficile à faire de manière optimale.
Les chercheurs ont déjà remarqué que les ensembles sur Kaggle: sont «très parfaits», et inspirés par les mots de Scholl et Hinton que la différenciation est le côté le plus faible du Deep Learning, ils ont décidé de créer un ensemble d'arbres aux propriétés DL.
Slide "Comment faire un bon ensemble"
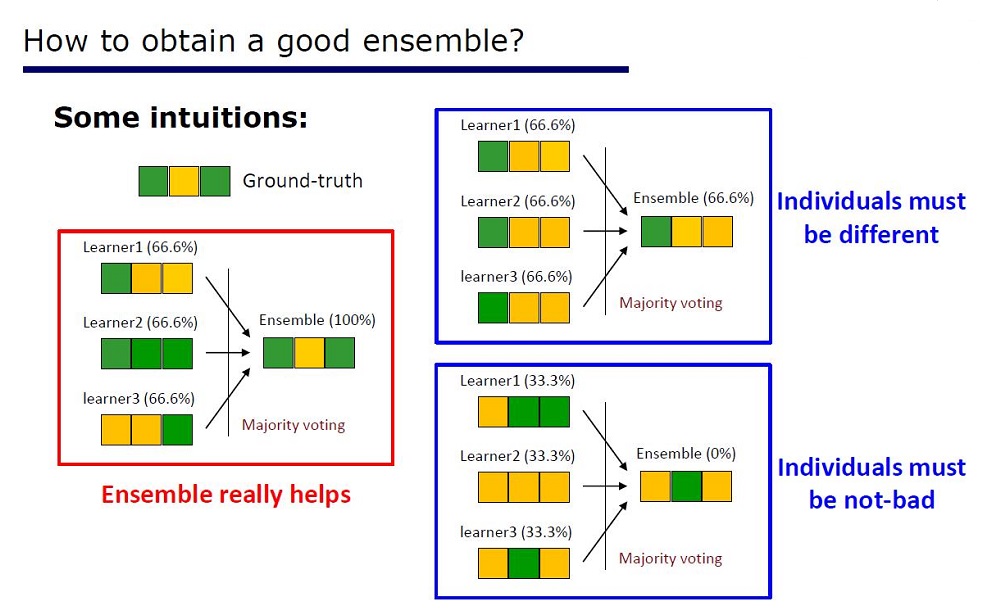
L'architecture a été déduite des propriétés des ensembles: les éléments des ensembles ne devraient pas être de très mauvaise qualité et différer.
GcForest se compose de deux phases: Cascade Forest et Multi-Grained Scanning. De plus, pour que la cascade ne se recycle pas, elle se compose de 2 types d'arbres - dont l'un est des arbres absolument aléatoires qui peuvent être utilisés sur des données non allouées. Le nombre de couches est déterminé à l'intérieur de l'algorithme de validation croisée.
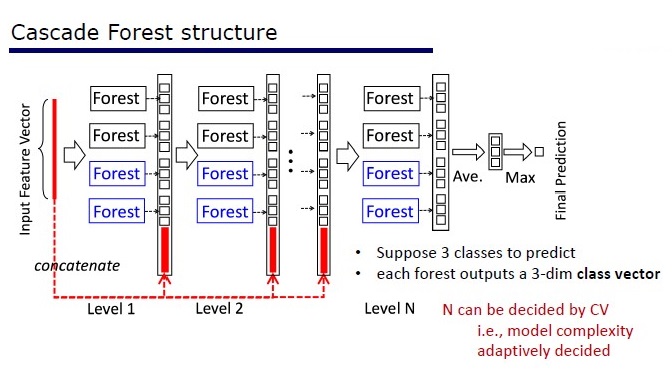
Deux types d'arbres
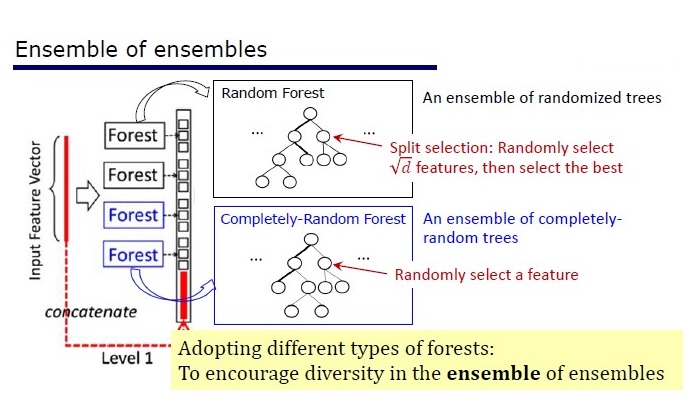
Résultats
En plus des résultats sur les ensembles de données standard, les auteurs ont essayé d'utiliser gcForest sur les transactions du système de paiement chinois pour rechercher la fraude et ont obtenu F1 et AUC beaucoup plus élevés que ceux de LR et DNN. Ces résultats ne sont que dans la présentation, mais le code à exécuter sur certains ensembles de données standard est sur Git.
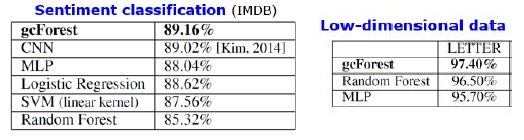
Résultats de substitution d'algorithme. mdDF est la distribution optimale des marges Deep Forest, une variante de gcForest
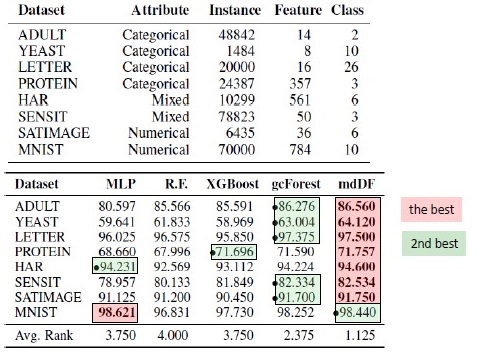
Avantages:
- Peu d'hyperparamètres, le nombre de couches est ajusté automatiquement à l'intérieur de l'algorithme
- Les paramètres par défaut sont choisis pour bien fonctionner sur de nombreuses tâches.
- Complexité adaptative du modèle, sur de petites données - un petit modèle
- Pas besoin de définir de fonctionnalités
- Il fonctionne de qualité comparable aux réseaux de neurones profonds, et parfois mieux
Inconvénients:
- Pas accéléré sur GPU
- Dans les images perd des DNN
Les réseaux de neurones ont un problème d'atténuation du gradient, tandis que la forêt profonde a un problème de «disparition de la diversité». Puisqu'il s'agit d'un ensemble, plus il y a d'éléments «différents» et «bons» à utiliser, meilleure est la qualité. Le problème est que les auteurs ont déjà essayé presque toutes les approches classiques (échantillonnage, randomisation). Tant qu'aucune nouvelle recherche fondamentale n'apparaîtra sur le thème des «différences», il sera difficile d'améliorer la qualité de la forêt profonde. Mais maintenant, il est possible d'améliorer la vitesse de calcul.
Reproductibilité des résultats
J'ai été intrigué par XGBoost sur les données tabulaires, et je voulais reproduire le résultat. J'ai pris le jeu de données Adultes et appliqué GcForestCS (une version légèrement accélérée de GcForest) avec les paramètres des auteurs de l'article et XGBoost avec les paramètres par défaut. Dans l'exemple que les auteurs avaient, les caractéristiques catégorielles étaient déjà prétraitées d'une manière ou d'une autre, mais il n'était pas indiqué comment. En conséquence, j'ai utilisé CatBoostEncoder et une autre métrique - ROC AUC. Les résultats étaient statistiquement différents - XGBoost a gagné. Le temps de fonctionnement de XGBoost est négligeable, tandis que gcForestCS dispose de 20 minutes de chaque validation croisée à 5 fois. D'autre part, les auteurs ont testé l'algorithme sur différents ensembles de données et ajusté les paramètres de cet ensemble de données à leur prétraitement d'entités.
Le code peut être trouvé ici .
Implémentations
→ Le code officiel des auteurs de l'article
→ Modification officielle améliorée, plus rapide, mais sans documentation
→ La mise en œuvre est plus simple
PcLasso: le lasso rencontre la régression des principaux composants
J. Kenneth Tay, Jerome Friedman, Robert Tibshirani (Université de Stanford)
→ Article
→ Présentation
→ Exemple d'utilisation
Début 2019, J.Kenneth Tay, Jerome Friedman et Robert Tibshirani de l'Université de Stanford ont proposé une nouvelle méthode d'enseignement avec un enseignant, particulièrement adaptée aux données rares.
Les auteurs de l'article ont résolu le problème de l'analyse des données sur les études d'expression génique, qui sont décrites dans Zeng & Breesy (2016). La cible est le statut mutationnel du gène p53, qui régule l'expression des gènes en réponse à divers signaux de stress cellulaire. Le but de l'étude est d'identifier les prédicteurs qui sont en corrélation avec le statut mutationnel de p53. Les données se composent de 50 lignes, dont 17 sont classées comme normales et les 33 autres portent des mutations dans le gène p53. Selon l'analyse de Subramanian et al. (2005) 308 ensembles de gènes compris entre 15 et 500 sont inclus dans cette analyse. Ces kits de gènes contiennent un total de 4 301 gènes et sont disponibles dans le package grpregOverlap R. Lors de l'expansion des données pour traiter les groupes qui se chevauchent, 13 237 colonnes sont sorties. Les auteurs de l'article ont utilisé la méthode pcLasso, qui a permis d'améliorer les résultats du modèle.
Dans l'image, nous voyons une augmentation de l'ASC lors de l'utilisation de "pcLasso"

L'essence de la méthode
La méthode combine  -régularisation avec
-régularisation avec  , qui rétrécit le vecteur de coefficients aux principaux composants de la matrice d'entités. Ils ont appelé la méthode proposée «composants principaux du lasso» («pcLasso» disponible sur R). La méthode peut être particulièrement puissante si les variables sont préalablement groupées (l'utilisateur choisit quoi et comment grouper). Dans ce cas, pcLasso compresse chaque groupe et obtient la solution en direction des principaux composants de ce groupe. Dans le processus de résolution, la sélection des groupes significatifs parmi ceux disponibles est également effectuée.
, qui rétrécit le vecteur de coefficients aux principaux composants de la matrice d'entités. Ils ont appelé la méthode proposée «composants principaux du lasso» («pcLasso» disponible sur R). La méthode peut être particulièrement puissante si les variables sont préalablement groupées (l'utilisateur choisit quoi et comment grouper). Dans ce cas, pcLasso compresse chaque groupe et obtient la solution en direction des principaux composants de ce groupe. Dans le processus de résolution, la sélection des groupes significatifs parmi ceux disponibles est également effectuée.
Nous présentons la matrice diagonale de la décomposition singulière d'une matrice centrée de traits  comme suit:
comme suit:
Nous représentons notre décomposition singulière de la matrice centrée X (SVD) comme  où
où  Est une matrice diagonale composée de valeurs singulières. Sous cette forme
Est une matrice diagonale composée de valeurs singulières. Sous cette forme  - La régularisation peut être représentée:
- La régularisation peut être représentée:
 où
où  - matrice diagonale contenant la fonction des carrés de valeurs singulières:
- matrice diagonale contenant la fonction des carrés de valeurs singulières: %2C%E2%80%A6%2CZ_%7B22%7D%3Df_2%20(d_1%5E2%2Cd_2%5E2%2C%E2%80%A6%2Cd_m%5E2%20)) .
.
En général, dans  -régularisation
-régularisation  pour tous
pour tous  cela correspond
cela correspond  . Ils suggèrent de minimiser les fonctionnalités suivantes:
. Ils suggèrent de minimiser les fonctionnalités suivantes:
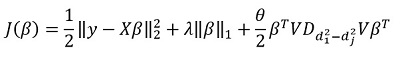
Ici  - matrice des différences d'éléments diagonaux
- matrice des différences d'éléments diagonaux  . En d'autres termes, nous contrôlons le vecteur
. En d'autres termes, nous contrôlons le vecteur  en utilisant également l'hyperparamètre
en utilisant également l'hyperparamètre  .
.
En transformant cette expression, nous obtenons la solution:
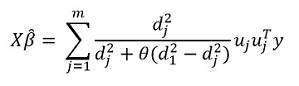
Mais la principale «caractéristique» de la méthode est, bien sûr, la capacité de regrouper les données et, sur la base de ces groupes, de mettre en évidence les principales composantes du groupe. Ensuite, nous réécrivons notre solution sous la forme:
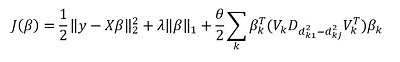
Ici  - sous-vecteur
- sous-vecteur  correspondant au groupe k,
correspondant au groupe k, ) - valeurs singulières
- valeurs singulières  classés par ordre décroissant, et
classés par ordre décroissant, et  - matrice diagonale
- matrice diagonale 
Quelques notes sur la solution de la fonctionnelle cible:
La fonction objectif est convexe et la composante non lisse est séparable. Par conséquent, il peut être efficacement optimisé en utilisant une descente de gradient.
L'approche consiste à valider plusieurs valeurs  (y compris zéro, respectivement, obtention de la norme
(y compris zéro, respectivement, obtention de la norme  -régularisation), puis optimiser:
-régularisation), puis optimiser:  ramasser
ramasser  . En conséquence, les paramètres
. En conséquence, les paramètres  et
et  sont sélectionnés pour la validation croisée.
sont sélectionnés pour la validation croisée.
Paramètre  difficile à interpréter. Dans le logiciel (package pcLasso), l'utilisateur définit lui-même la valeur de ce paramètre, qui appartient à l'intervalle [0,1], où 1 correspond à
difficile à interpréter. Dans le logiciel (package pcLasso), l'utilisateur définit lui-même la valeur de ce paramètre, qui appartient à l'intervalle [0,1], où 1 correspond à  = 0 (lasso).
= 0 (lasso).
En pratique, faire varier les valeurs  = 0,25, 0,5, 0,75, 0,9, 0,95 et 1, vous pouvez couvrir une large gamme de modèles.
= 0,25, 0,5, 0,75, 0,9, 0,95 et 1, vous pouvez couvrir une large gamme de modèles.
L'algorithme lui-même est le suivant

Cet algorithme est déjà écrit en R, si vous le souhaitez, vous pouvez déjà l'utiliser. La bibliothèque s'appelle 'pcLasso'.
Un couteau suisse infinitésimal
Ryan Giordano (UC Berkeley); William Stephenson (MIT); Runjing Liu (UC Berkeley);
Michael Jordan (UC Berkeley); Tamara Broderick (MIT)
→ Article
→ Code
La qualité des algorithmes d'apprentissage automatique est souvent mesurée par plusieurs validations croisées (validation croisée ou bootstrap). Ces méthodes sont puissantes, mais lentes sur les grands ensembles de données.
Dans ce travail, les collègues utilisent une approximation linéaire des poids, produisant des résultats qui fonctionnent plus rapidement. Cette approximation linéaire est connue dans la littérature statistique sous le nom de «jackknife infinitésimal». Il est principalement utilisé comme outil théorique pour prouver des résultats asymptotiques. Les résultats de l'article sont applicables, que les poids et les données soient stochastiques ou déterministes. Par conséquent, cette approximation estime séquentiellement la véritable validation croisée pour tout k fixe.
Remise du Paper Award à l'auteur de l'article

L'essence de la méthode
Considérez le problème de l'estimation d'un paramètre inconnu  où
où  Est compact et la taille de notre jeu de données est
Est compact et la taille de notre jeu de données est  . Notre analyse sera réalisée sur un ensemble de données fixes. Définissez notre note
. Notre analyse sera réalisée sur un ensemble de données fixes. Définissez notre note  comme suit:
comme suit:
- Pour chacun
 ensemble
ensemble  (
(  ) Est fonction de
) Est fonction de 
 Est un nombre réel, et
Est un nombre réel, et  Est un vecteur composé de
Est un vecteur composé de 
Alors  peut être représenté comme:
peut être représenté comme:

En résolvant ce problème d'optimisation par la méthode du gradient, nous supposons que les fonctions sont différenciables et nous pouvons calculer la Hesse. Le principal problème que nous résolvons est le coût de calcul associé à l'évaluation ) pour tous
pour tous  . La principale contribution des auteurs de l'article consiste à calculer l'estimation
. La principale contribution des auteurs de l'article consiste à calculer l'estimation ) où
où ) . En d'autres termes, notre optimisation ne dépendra que des dérivés
. En d'autres termes, notre optimisation ne dépendra que des dérivés ) que nous supposons exister et sont hessois:
que nous supposons exister et sont hessois:
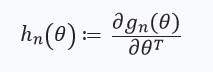
Ensuite, nous définissons une équation avec un point fixe et sa dérivée:
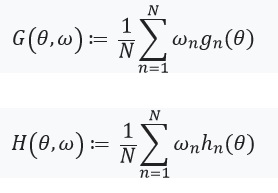
Ici, il convient de faire attention à ce que %2Cw)%3D0) depuis
depuis ) - solution pour
- solution pour %3D0) . Nous définissons également:
. Nous définissons également: ) , et la matrice de poids comme:
, et la matrice de poids comme:  . Dans le cas où
. Dans le cas où  a une matrice inverse, nous pouvons utiliser le théorème de fonction implicite et la «règle de chaîne»:
a une matrice inverse, nous pouvons utiliser le théorème de fonction implicite et la «règle de chaîne»:
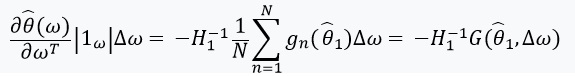
Cette dérivée nous permet de former une approximation linéaire ) à travers
à travers  qui ressemble à ceci:
qui ressemble à ceci:
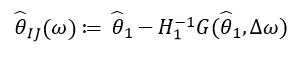
Depuis  ne dépend que de
ne dépend que de  et
et  , et non à partir de solutions pour d'autres valeurs
, et non à partir de solutions pour d'autres valeurs  , en conséquence, il n'est pas nécessaire de recalculer et de trouver de nouvelles valeurs de ω. Au lieu de cela, il faut résoudre le SLE (système d'équations linéaires).
, en conséquence, il n'est pas nécessaire de recalculer et de trouver de nouvelles valeurs de ω. Au lieu de cela, il faut résoudre le SLE (système d'équations linéaires).
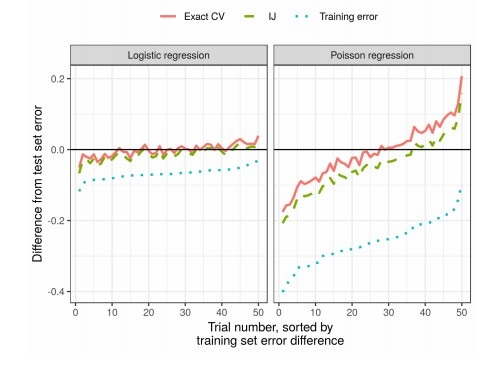
Résultats
En pratique, cela réduit considérablement le temps par rapport à la validation croisée: