Alexey Savvateev: Modèles d'Internet et des réseaux sociaux

"La seule raison de l'existence de l'économie est d'inspirer les mathématiciens à de nouveaux exploits."



En 2013, Alexey Savvateev a donné plusieurs conférences sur les modèles de réseaux sociaux et Internet. J'ai trouvé ce sujet très curieux et oublié à juste titre. Essayons de comprendre le problème. Je suis également intéressé de savoir comment la situation a évolué depuis lors et quelles sont les publications utiles dans ce domaine.

À la fois sur Internet et dans la biologie des réseaux sociaux, ils présentent des propriétés décrites individuellement par des modèles, mais tous ensemble - ils confondent les mathématiques modernes. Savvateev affirme que "celui qui s'en occupera recevra le prix Nobel". L'avenir dépendra de la capacité à travailler avec des réseaux.

Ce qui suit est une compression compilée de trois vidéos de conférence, la vidéo elle-même est à la fin. (Le message ressemble à un ensemble de diapositives avec des citations de conférencier, pour tout lier en un texte unique et élégant, je n'ai pas les compétences en russe et en mathématiques, mais le sujet est très important, donc je veux le publier.)

Le réseau social est composé de:

• Agents
• Communications entre agents

Les connexions peuvent être bidirectionnelles (amis, coauteurs) et peuvent être unidirectionnelles (abonnés). Les réseaux sociaux ont toujours existé, mais les étudier au niveau macro n'est devenu possible qu'avec l'avènement des réseaux en ligne. L'humanité au cours des 10 dernières années a fait un bond en avant. Il a appris à s'interroger sur lui-même dans son ensemble. Il peut numériser. Rassemblez des informations sur vous-même.

Il serait juste de construire un modèle de graphiques pondérés lorsque les coefficients de la «force de liaison» sont indiqués. Mais pour nous comme avant à la lune.

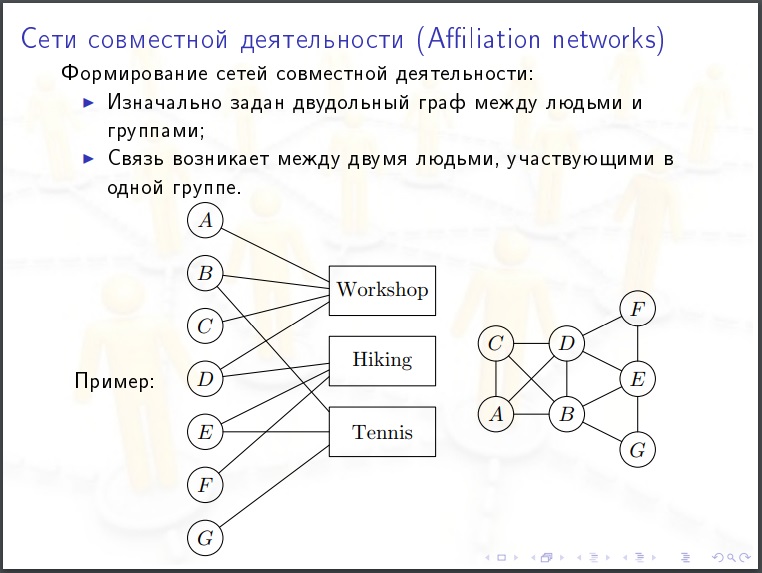
Galerie

Il est utile de regarder les photos. L'hypothèse que vous pourriez avancer après avoir visionné l'image peut être évidemment absurde.

Qui est utile pour étudier les réseaux sociaux

Économie: On suppose que les niveaux micro et macro de l'économie sont connectés via un «réseau»
Science politique: On suppose que le régime restera ou changera, selon qui aura des spécialistes de réseau plus puissants.



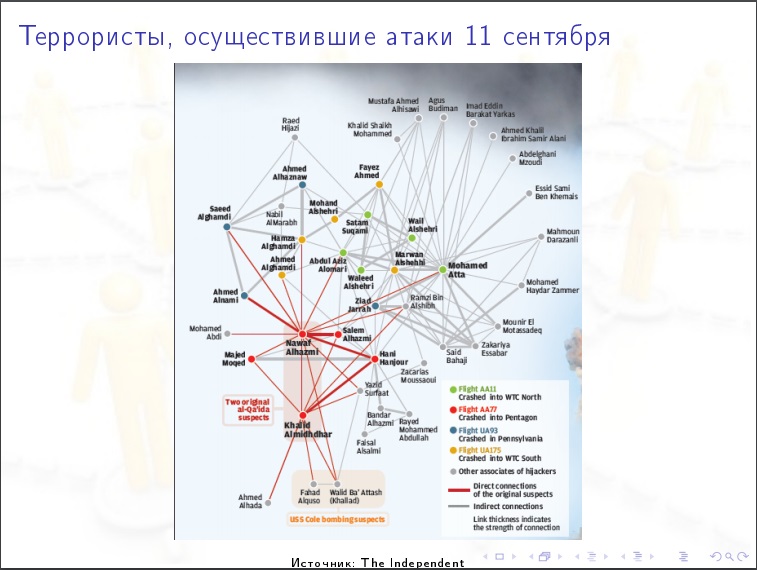Exemple d'analyse des médias sociaux.

Caractéristiques numériques des réseaux sociaux

• La distance
• Diamètre
• Degré de sommet
• Distribution des degrés de sommet
• Mesures de centralité des nœuds
• Distribution de centralité
• Coefficient de regroupement
• Coefficient d'assortiment

Distance - combien d'arêtes vous devez passer pour passer d'un sommet à un autre.

Le diamètre est la distance maximale dans le graphique.

Le degré d'un sommet est le nombre d'arêtes au sommet.

Théorie des six poignées de main

Tout graphique social a un diamètre moyen très faible ( théorie des six poignées de main ). De plus, il y a un noyau très dense. Je suis "familier" avec certains Africains, à travers mon président, qui ont serré la main du président africain.







Coefficient de regroupement local . Nous regardons tous les voisins d'une personne, des morceaux "k". Nervures maximales - k (k-1) / 2. Nous regardons le nombre réel d'arêtes et divisons par ce maximum.

Facteur de cluster global . Combien de «triangles» par rapport aux «coches».





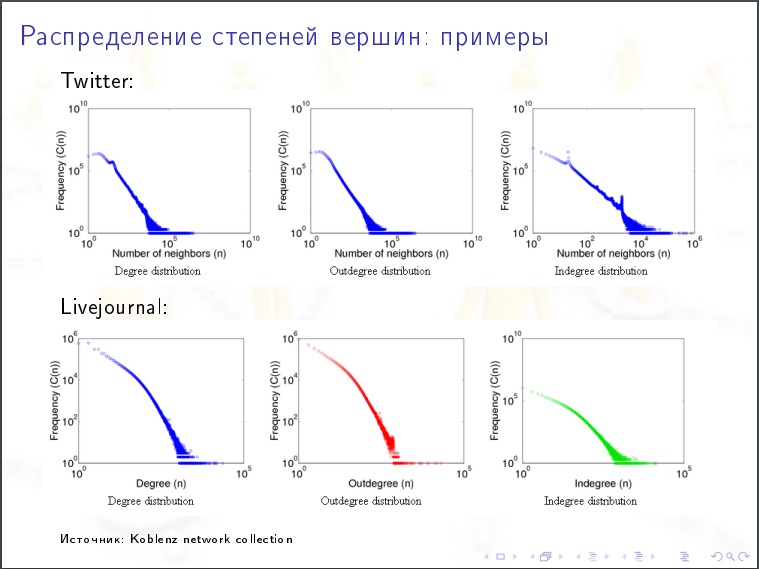
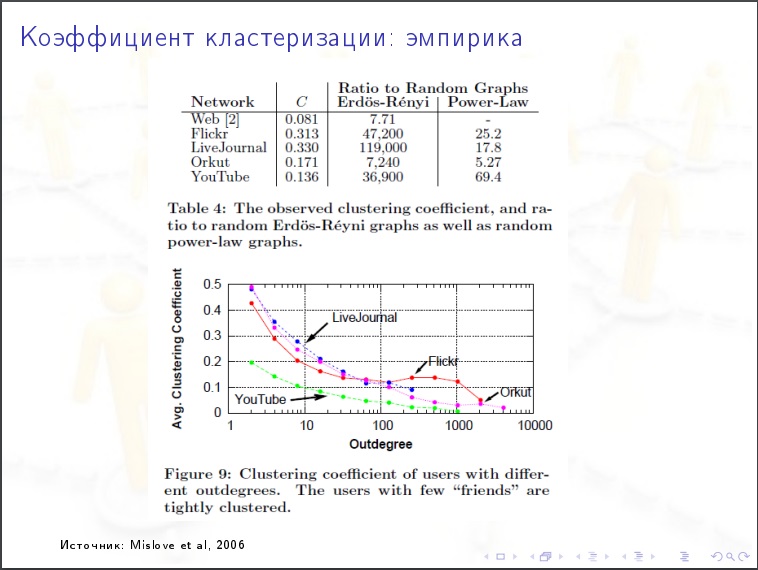La distribution des degrés du sommet . Quel% des sommets a des degrés inférieurs à 1000? La nature de la distribution est-elle exponentielle ou exponentielle? Il s'avère que l'Internet a un caractère calme.

Le coefficient est "2". Les sommets dont le degré est «x» seront N / x ² . Nous vérifions que dans un milliard d'utilisateurs de LJ, les millièmes doivent être divisés par mille à mille carrés. Mille millièmes.

C'est une chose qui diminue très lentement.













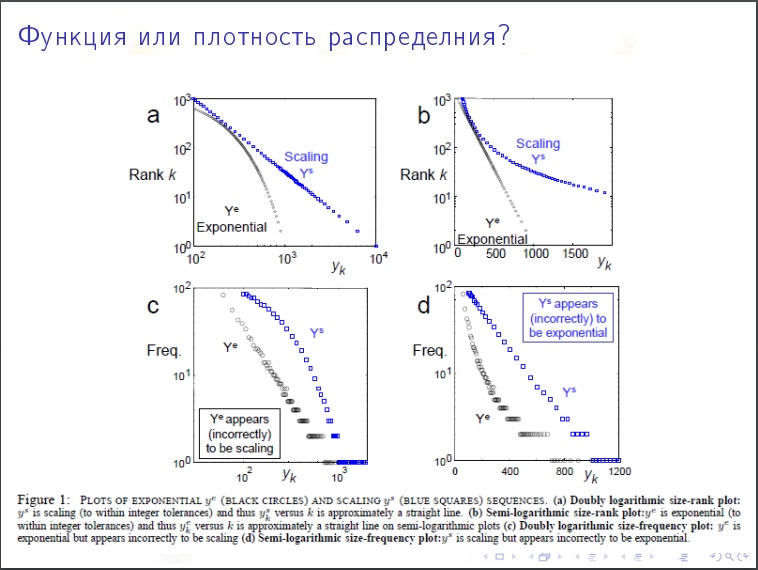
Coefficient d'assortiment . approche approximative - nous prenons des pics avec approximativement le même nombre de degrés, sont-ils plus susceptibles d'être connectés les uns aux autres ou avec moins? Si oui, alors il est assorti. Dissortivité - quand avec un grand nombre de degrés sont plus susceptibles d'être associés à moins. Il s'agit d'une approche naïve. Une approche plus correcte est la suivante. À chaque sommet, il existe une autre caractéristique (capital total de la banque), et l'assortiment de cet indicateur semble.





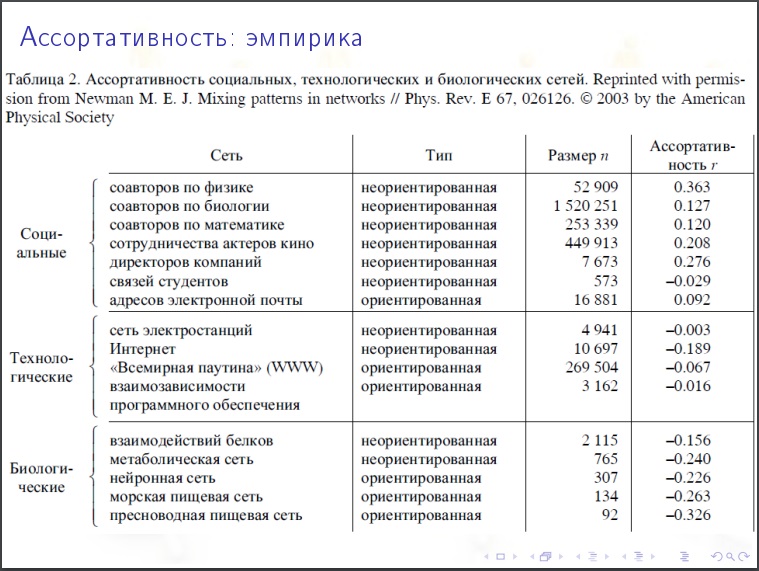La centralité du nœud pour un réseau social. Nous prenons une personne, nous considérons la valeur suivante pour elle. Nous trions toutes les paires d'autres personnes (N-1) (N-2) / 2 et dans chaque cas nous demandons, le chemin de datation le plus proche dans le graphique, passe-t-il par cette personne? Il peut y avoir plusieurs chemins les plus courts et certains d'entre eux contiennent notre personne, alors nous lui donnons%. C'est la caractéristique la plus importante des réseaux sociaux. Pour la propagation des épidémies, l'opinion publique. C'est ce qui doit être mesuré.









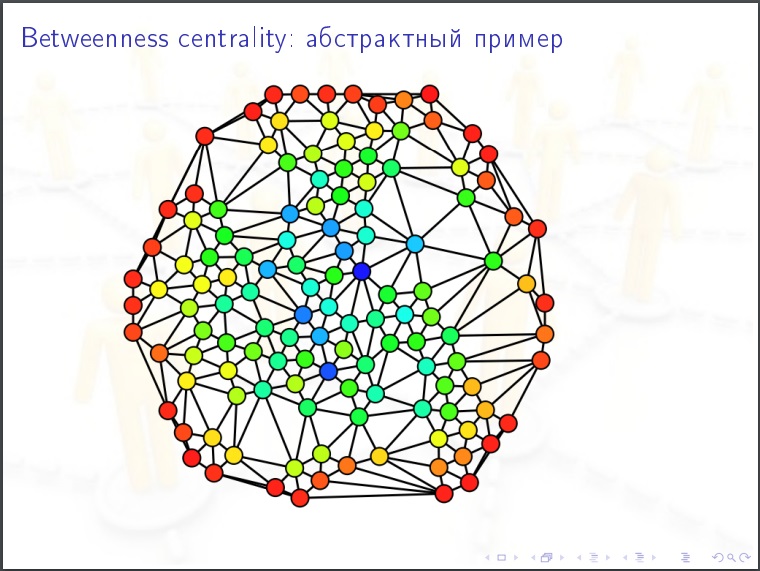
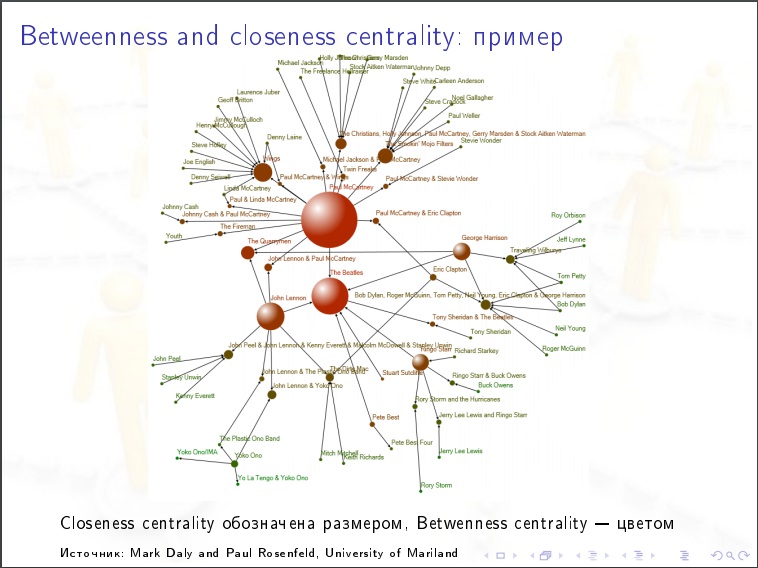
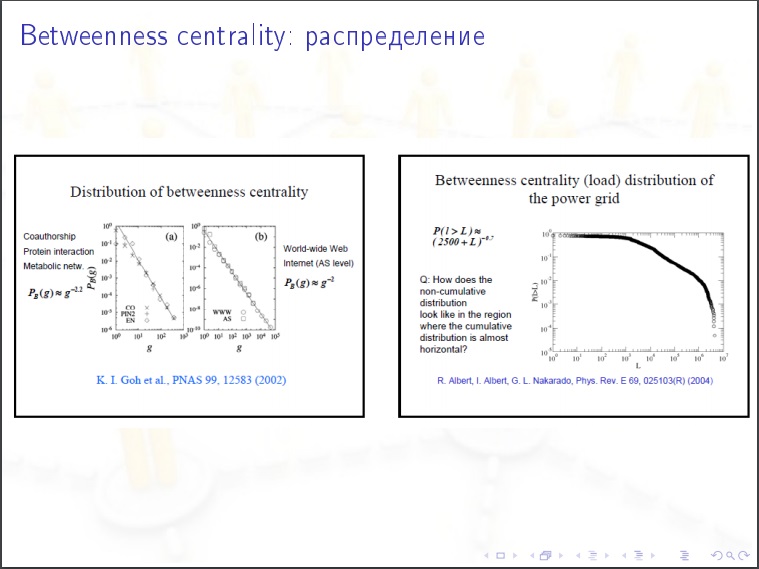
Caractéristiques des réseaux sociaux:

• Petit diamètre et distance moyenne entre les sommets
• La loi de puissance de la distribution des degrés de sommets et la centralité de l'interdépendance
• Ratio de clustering élevé
• Assortiment
• La présence d'un noyau étroitement lié

La tâche consiste à créer un modèle qui couvre les trois premières propriétés (et de préférence les deux dernières). Les trois premiers sont déjà d'une complexité insurmontable à l'heure actuelle. Pour 2013, il n'y a pas un tel modèle.

Nous passons à la description des modèles de graphes aléatoires qui existaient.

Les modèles

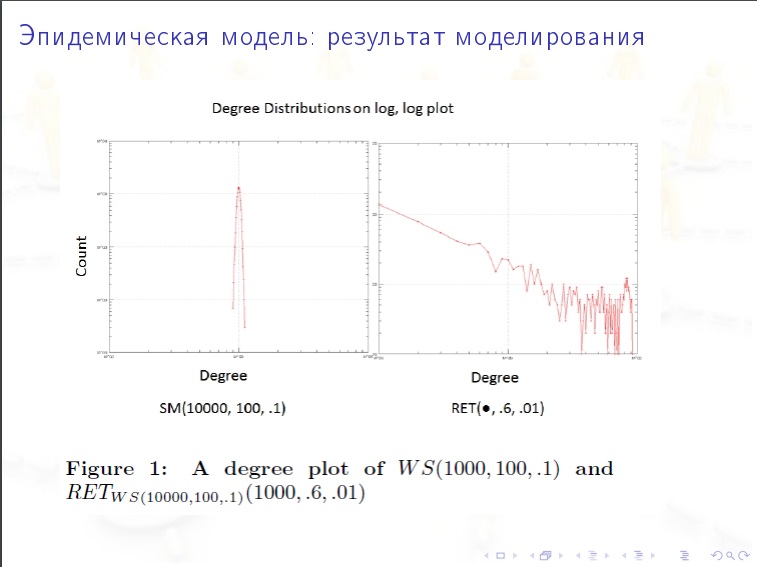
Les modèles sont:

• Technique (les bords sont générés aléatoirement)
• Théorie des jeux (quand cela profite à quelqu'un)
• Pas de structure (juste beaucoup de sommets)
• Structurel (les sommets sont des points de l'espace métrique ou ont des poids; il y a une structure sur l'ensemble des sommets)

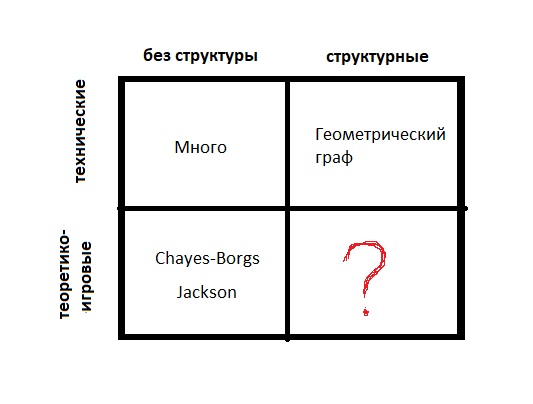
Si vous comprenez ce qui sous-tend, vous pouvez être guidé par un très grand nombre de paramètres. Si des paramètres bien choisis donnent une bonne approximation, alors vous avez bien fait. Et même si la meilleure combinaison donne un mauvais résultat et n'est pas conforme aux faits observés, alors au revoir.

Tout cela est fait dans un seul but: lutter contre le spam.

Internet peut être imaginé comme un réseau complexe à plusieurs niveaux:

• Niveau technologique . Les sommets et les arêtes sont des nœuds et des lignes de communication.
• Niveau hypertexte . Les sommets sont des sites ou des pages et les bords sont des hyperliens.
• Niveau social . Les sommets sont des utilisateurs, et les bords sont ceux ou d'autres connexions entre eux: amitiés sur les réseaux sociaux, abonnement à des blogs, collaboration dans des projets distribués (par exemple wikipedia), etc.

Pour les réseaux complexes, de nombreuses caractéristiques numériques locales et globales sont connues: la distribution des degrés de sommets, le coefficient de clustering, le coefficient d'assortivité

Il s'avère qu'un certain nombre de fonctionnalités sont caractéristiques des réseaux Internet:

• Distribution de Paretto des degrés
• coefficient de clustering élevé,
• assortiment positif
• petit diamètre.

Le but ultime de la modélisation des réseaux Internet est de construire des modèles avec les mêmes fonctionnalités.

Modèle Erdos - Renyi

Le modèle Erdos-Renyi est l'un des deux modèles de génération de graphes aléatoires étroitement liés. Les modèles portent le nom des mathématiciens Pal Erdös et Alfred Renyi, qui ont été les premiers à introduire l'un des modèles en 1959. A exploré le graphique de datation.

Considérez N points. Bords potentiels - N * (N-1) / 2. Pour chaque côte, nous effectuons un test aléatoire. La probabilité que la côte se soit produite - p. Ce qui ne s'est pas produit - (1-p). Lançons le «test», nous obtenons un graphique. Mais il y a quelques problèmes. Pour que la propriété «clairsemée» apparaisse, p doit être très petit, de l'ordre de 1 / N, puis le diamètre sera très grand.

Tout chercheur qui entend que l'Internet est décrit comme un graphique aléatoire selon le modèle Erds-Renyi va rire.

Un effet intéressant est que lorsque vous dépassez un certain seuil de probabilité, le graphique devient connecté.

Modèle Bollobashi

Il s'agit d'un modèle dynamique de construction d'Internet. Nous essayons de deviner comment il s'est formé progressivement. L'idée est la suivante. Nous prenons un graphique avec un sommet et une arête, puis à chaque étape, nous jouons au hasard. Nous ajoutons un sommet, après quoi, avec une certaine probabilité, il se ferme sur lui-même, et avec une certaine probabilité se connecte au précédent. Le prochain pic avec une certaine probabilité se ferme sur lui-même, et avec certains va à l'un des précédents. De plus, la probabilité de toucher le sommet est toujours proportionnelle au nombre d'arêtes qui le sont. Une valeur aléatoire est jouée et le prochain tirage dépend du résultat du précédent. Un tel modèle est intuitif, mais mathématiquement difficile à calculer. Ce modèle donne une distribution de puissance non exponentielle. Le diamètre est le même.

Mais ce modèle ne fonctionne pas avec le clustering.

Il existe deux approches concurrentes qui fonctionnent avec le clustering.

Approche géométrique

L'hypothèse est tirée du plafond. Le graphique Internet est basé sur l'espace métrique. L'espace des goûts, des intérêts, des préférences. Comme les gens sont intéressants les uns pour les autres. Quelle proximité dans l'esprit, dans l'opinion. Si les gens sont proches, ils se réfèrent l'un à l'autre.

Nous prenons et jetons 10 ¹⁰ points dans cet espace. Un grand nombre de paramètres apparaissent ici. Énorme

Le regroupement est excellent, mais les sommets décroissants sont exponentiels. Controverse.

Cette méthode est terriblement simple et les algorithmes se font «par hasard».

Game-Borgs approche théorique du jeu

Saviez-vous qu'au temps de von Neumann, il a été annoncé que la théorie des jeux serait une arme de nouvelle génération contre l'Union soviétique?

Nous supposons que les gens prennent des décisions pour communiquer entre eux ou non.

Nous organisons des réunions / événements. Un événement est une liste d'invités, ainsi que son «intensité».
Coûts = Intensité * (constante + K * (nombre d'invités)). Je dois dépenser des ressources pour «vendre» l'événement et je dois dépenser plus pour chaque participant. Il y a des anniversaires et des randonnées. Le coefficient "P" apparaît, qui est petit pour un anniversaire et grand pour une randonnée. Rencontres d'intensité.

Une personne peut organiser plusieurs événements avec des intensités P ₁ , P ₂ ... P _n . D'autres font de même.

Il y a mes actions pour établir des liens sociaux, et il y a des étrangers.

Fonction gagnante = (le nombre de personnes avec lesquelles vous vous êtes familiarisé) - coûts

«Assez familier» signifie que la somme des intensités de tous les événements où vous étiez ensemble est supérieure à une certaine valeur seuil. Et peu importe qui a organisé l'événement.

Les côtes sont tenues pour de bonnes connaissances.



Il est prouvé que de nombreuses propriétés de fermeture réelle sont obtenues dans ce modèle. Dans tous les équilibres de Nash, des propriétés de fermeture réelles et des propriétés de regroupement encore plus fortes sont également observées, qui sont également observées sur le graphique de l'Internet réel.



Mais rien n'est clair sur les autres propriétés, mais c'est la moitié du problème. Le problème est que s'il y a au moins un équilibre de Nash où au moins deux personnes se connaissent, alors il y a un équilibre de Nash dans lequel tout le monde est familier avec tout le monde.





Il y a une idée pour combiner les deux approches. Pour considérer que les gens vivent dans un espace métrique, et lorsqu'ils organisent des événements ou participent à un événement, le coût, l'intensité et les ratios de seuil dépendent de la «proximité». Il s'agit de la cinquième génération de modèles.

Coûts différenciés

Les options sont de faire des coûts différenciés et des gains différenciés. Certains sont plus faciles à inviter que d'autres. La connaissance de l'un est plus rentable que la connaissance de l'autre.





Supposons que nous disposions toutes les personnes uniformément autour de la circonférence. Et c'est moins cher d'inviter quelqu'un qui est plus proche. À quoi ressemblera l'équilibre? Tout le monde invitera un quartier, non? Pas vrai. Il n'y a pas un tel équilibre.

Preuve. Supposons qu'il existe, alors les personnes proches les unes des autres sont déjà invitées à de nombreuses réunions différentes. Ensuite, il n'a pas besoin d'inviter cet être cher. L'existence de cet équilibre contredit l'existence de cet équilibre.



L'équilibre pur existe, il se trouve, c'est le seul. Chacun invite un quartier qui se trouve (ou dans le sens antihoraire) à une certaine distance de lui et une certaine longueur.

(- C'est la formation de galaxies!)
(- C'est une rupture de symétrie spontanée!)

Conclusions

Pelevin a écrit un jour que «le sens de la vie russe est dans la dorure sans hâte d'une immense iconostase». C'est le sens des mathématiques - dans le même sens. Seule l'iconostase est scientifique.



Il s'agit d'une étude hautement multidisciplinaire. Plus haut que vous pouvez l'imaginer.

Les sources

PS

«Une fois que j'ai été appelé au club de Navalny, il y a des jeunes, des passionnés qui l'aident. J'ai immédiatement averti que je dirais des choses désagréables. Une révolution est victorieuse si les mathématiciens qui sont pour la révolution sont plus forts que ceux qui sont contre. Les jeunes de Navalny ne savaient pas comment leur dire de tels modèles, mais ils ne comprennent pas, ils ne savent même pas comment s’intégrer - ils courent et crient quelque part. Et contre eux se trouve une institution forte avec à sa tête des gens sérieux qui, sur ordre du Kremlin, disent qui exactement et combien doivent être arrêtés pour qu'il n'y ait rien. Ils disent: "Nous sommes décentralisés - spécifiquement Navalny ne veut rien dire, il y a plusieurs dirigeants importants." Et puis un mathématicien vient et croit que la centralisation représente 90% de ce réseau. Vous bloquez quelqu'un dont vous avez besoin pendant quelques jours - et il n'y a pas de révolution. Les maths gagnent. "
- Alexey Savvateev, «La révolution gagne si elle a de bons mathématiciens»

PPS

Qui sait quels autres travaux intéressants (articles, conférences) il y a des travaux dans le domaine des réseaux sociaux et leurs avantages pratiques, veuillez partager.