Réseaux de neurones et apprentissage profond, chapitre 3, partie 1: améliorer la formation des réseaux de neurones

Lorsqu'une personne apprend à jouer au golf, elle passe généralement la plupart de son temps à organiser un coup basique. Il aborde ensuite progressivement d'autres coups, étudiant ces ou ces tours, en fonction du coup de base et en le développant. De même, nous nous sommes jusqu'à présent concentrés sur la compréhension de l'algorithme de rétropropagation. Il s'agit de notre «grève de base», la base de la formation pour la plupart des travaux avec les réseaux de neurones (NS). Dans ce chapitre, je parlerai d'un ensemble de techniques qui peuvent être utilisées pour améliorer notre mise en œuvre plus simple de la rétropropagation et pour améliorer la façon d'enseigner la NS.

Parmi les techniques que nous allons apprendre dans ce chapitre: la meilleure option pour le rôle de la fonction de coût, à savoir la fonction de coût avec entropie croisée; quatre soi-disant les méthodes de régularisation (régularisation de L1 et L2, exclusion des neurones [décrochage], extension artificielle des données d'entraînement), qui améliorent la généralisation de notre NS au-delà des limites des données d'entraînement; meilleure méthode pour initialiser les pondérations du réseau; un ensemble de méthodes heuristiques pour vous aider à choisir de bons hyperparamètres pour le réseau. J'examinerai également plusieurs autres techniques, un peu plus superficiellement. Pour la plupart, ces discussions sont indépendantes les unes des autres, vous pouvez donc les sauter si vous le souhaitez. Nous implémentons également de nombreuses technologies dans le code de travail et les utilisons pour améliorer les résultats obtenus pour la tâche de classification des nombres manuscrits, étudiée au chapitre 1.

Bien sûr, nous ne considérons qu'une fraction du grand nombre de techniques développées pour être utilisées avec les réseaux de neurones. L'essentiel est que la meilleure façon d'entrer dans le monde de l'abondance des techniques disponibles est d'étudier en détail quelques-unes des plus importantes. La maîtrise de ces techniques importantes n'est pas seulement utile en soi, elle approfondira également votre compréhension des problèmes pouvant survenir lors de l'utilisation de réseaux de neurones. En conséquence, vous serez prêt à adapter rapidement de nouvelles techniques au besoin.

Fonction de coût d'entropie croisée

La plupart d'entre nous détestent se tromper. Peu de temps après avoir commencé à apprendre le piano, j'ai donné un petit concert devant un public. J'étais nerveux et j'ai commencé à jouer un morceau une octave plus bas que nécessaire. J'étais confus et ne pouvais pas continuer jusqu'à ce que quelqu'un me signale une erreur. J'avais très honte. Cependant, bien que ce soit désagréable, nous apprenons aussi très rapidement, décidant que nous nous trompions. Et certainement la prochaine fois que j'ai parlé au public, j'ai joué dans la bonne octave! À l'inverse, nous apprenons plus lentement lorsque nos erreurs ne sont pas bien définies.

Idéalement, nous nous attendons à ce que nos réseaux de neurones apprennent rapidement de leurs erreurs. Cela se produit-il dans la pratique? Pour répondre à cette question, regardons un exemple farfelu. Il s'agit d'un neurone avec une seule entrée:



Nous enseignons à ce neurone à faire quelque chose de ridiculement simple: accepter 1 et donner 0. Bien sûr, nous pourrions trouver une solution à un problème aussi trivial en sélectionnant manuellement le poids et l'offset, sans utiliser l'algorithme d'entraînement. Cependant, il sera très utile d'essayer d'utiliser la descente en pente pour obtenir le poids et le déplacement à la suite de l'entraînement. Voyons comment un neurone est entraîné.

Pour être précis, je choisirai un poids initial de 0,6 et un décalage initial de 0,9. Ce sont des valeurs générales assignées comme point de départ, et je ne les ai pas sélectionnées spécifiquement. Initialement, un neurone de sortie produit 0,82, nous devons donc en apprendre beaucoup pour nous rapprocher de la sortie souhaitée de 0,0. L' article original a un formulaire interactif sur lequel vous pouvez cliquer sur "Exécuter" et observer le processus d'apprentissage. Cette animation n'est pas préenregistrée, le navigateur calcule en fait le gradient, puis l'utilise pour mettre à jour le poids et le décalage, et affiche le résultat. La vitesse d'apprentissage est η = 0,15, suffisamment lente pour pouvoir voir ce qui se passe, mais suffisamment rapide pour que l'apprentissage se déroule en quelques secondes. La fonction de coût C est quadratique, introduite dans le premier chapitre. Je vais bientôt vous rappeler sa forme exacte, il n'est donc pas nécessaire d'y revenir pour y fouiller. La formation peut être lancée plusieurs fois en cliquant simplement sur le bouton «Exécuter».

Comme vous pouvez le voir, le neurone apprend rapidement le poids et le biais, ce qui réduit le coût et donne une sortie de 0,09. Ce n'est pas tout à fait le résultat souhaité de 0,0, mais plutôt bon. Supposons que nous choisissions un poids initial et un décalage de 2,0 à la place. Dans ce cas, la sortie initiale sera de 0,98, ce qui est complètement faux. Voyons comment dans ce cas le neurone apprendra à produire 0.

Bien que cet exemple utilise le même taux d'apprentissage (η = 0,15), nous constatons que l'apprentissage est plus lent. Environ 150 des premières époques, poids et déplacements ne changent guère. Ensuite, l'entraînement s'accélère et, presque comme dans le premier exemple, le neurone se déplace rapidement à 0,0. ce comportement est étrange, pas comme apprendre une personne. Comme je l'ai dit au début, nous apprenons souvent plus rapidement lorsque nous nous trompons beaucoup. Mais nous venons de voir comment notre neurone artificiel apprend avec beaucoup de difficulté, faisant beaucoup d'erreurs - beaucoup plus difficile que lorsqu'il a fait une petite erreur. De plus, il s'avère que ce comportement survient non seulement dans notre exemple simple, mais aussi dans un NS à usage plus général. Pourquoi l'apprentissage est-il si lent? Puis-je trouver un moyen d'éviter ce problème?

Pour comprendre la source du problème, nous rappelons que notre neurone apprend par des changements de poids et de déplacement à un taux déterminé par les dérivées partielles de la fonction de coût, ∂C / ∂w et ∂C / ∂b. Donc, dire «l'apprentissage est lent» revient à dire que ces dérivées partielles sont petites. Le problème est de comprendre pourquoi ils sont petits. Pour ce faire, calculons les dérivées partielles. Rappelons que nous utilisons la fonction de coût quadratique, qui est donnée par l'équation (6):

$$

$$C = \ frac {(y-a) ^ 2} {2} \ tag {54}$$

où a est la sortie du neurone lorsque x = 1 est utilisé à l'entrée et y = 0 est la sortie souhaitée. Pour écrire cela directement par le poids et le déplacement, rappelons que a = σ (z), où z = wx + b. En utilisant la règle de chaîne pour la différenciation en poids et en déplacement, nous obtenons:

$$

$$\ frac {\ partial C} {\ partial w} = (a-y) \ sigma '(z) x = a \ sigma' (z) \ tag {55}$$

$$

$$\ frac {\ partial C} {\ partial b} = (a-y) \ sigma '(z) = a \ sigma' (z) \ tag {56}$$

où j'ai substitué x = 1 et y = 0. Pour comprendre le comportement de ces expressions, regardons de plus près le terme σ '(z) à droite. Rappelez-vous la forme d'un sigmoïde:



Le graphique montre que lorsque la sortie du neurone est proche de 1, la courbe devient très plate et σ '(z) devient petite. Les équations (55) et (56) nous indiquent que ∂C / ∂w et ∂C / ∂b deviennent très petits. D'où le ralentissement de l'apprentissage. De plus, comme nous le verrons un peu plus tard, le ralentissement de la formation se produit, en fait, pour la même raison et à l'Assemblée nationale de manière plus générale, et pas seulement dans notre exemple le plus simple.

Présentation de la fonction de coût d'entropie croisée

Que faisons-nous pour ralentir l'apprentissage? Il s'avère que nous pouvons résoudre le problème en remplaçant la fonction quadratique de valeur par une autre fonction de valeur, appelée entropie croisée. Pour comprendre l'entropie croisée, nous nous éloignons de notre modèle le plus simple. Supposons que nous entraînions un neurone avec plusieurs valeurs d'entrée x ₁ , x ₂ , ... poids correspondants w ₁ , w ₂ , ... et décalage b:



La sortie du neurone, bien sûr, sera a = σ (z), où z = ∑ _j w _j x _j + b est la somme pondérée des entrées. Nous définissons la fonction de coût d'entropie croisée pour un neurone donné comme

$$

$$C = - \ frac {1} {n} \ sum_x \ left [y \ ln a + (1-y) \ ln (1-a) \ right] \ tag {57}$$

où n est le nombre total d'unités de données d'apprentissage, la somme passe par toutes les données d'apprentissage x et y est la sortie souhaitée correspondante.

Il n'est pas évident que l'équation (57) résout le problème du ralentissement de l'apprentissage. Honnêtement, il n'est même pas évident qu'il soit logique d'appeler cela une fonction de valeur! Avant d'aborder le ralentissement de l'apprentissage, voyons dans quel sens l'entropie croisée peut être interprétée en fonction de la valeur.

Deux propriétés en particulier permettent d'interpréter l'entropie croisée en fonction de la valeur. Tout d'abord, il est supérieur à zéro, c'est-à-dire C> 0. Pour voir cela, notez que (a) tous les membres individuels de la somme en (57) sont négatifs, car les deux logarithmes sont tirés de nombres compris entre 0 et 1, et (b) le signe moins est devant la somme.

Deuxièmement, si la sortie réelle du neurone est proche de la sortie souhaitée pour toutes les entrées d'apprentissage x, alors l'entropie croisée sera proche de zéro. Pour le prouver, nous devrons supposer que les sorties souhaitées y seront 0 ou 1. Habituellement, cela se produit lors de la résolution de problèmes de classification ou du calcul de fonctions booléennes. Pour comprendre ce qui se passe si vous ne faites pas une telle hypothèse, reportez-vous aux exercices à la fin de la section.

Pour le prouver, imaginez que y = 0 et a≈0 pour une entrée x. Il en sera de même lorsque le neurone gérera bien une telle entrée. Nous voyons que le premier terme d'expression (57) pour la valeur disparaît, car y = 0, et le second sera −ln (1 - a) ≈0. Il en va de même lorsque y = 1 et a≈1. Par conséquent, la contribution de la valeur sera faible si la sortie réelle est proche de celle souhaitée.

En résumé, nous obtenons que l'entropie croisée est positive et tend à zéro lorsque le neurone calcule mieux la sortie souhaitée y pour toutes les entrées d'apprentissage x. Nous nous attendons à la présence des deux propriétés dans la fonction de coût. Et en effet, ces deux propriétés sont remplies par la valeur quadratique. Par conséquent, pour l'entropie croisée, c'est une bonne nouvelle. Cependant, la fonction de coût d'entropie croisée présente un avantage car, contrairement à la valeur quadratique, elle évite le problème de ralentissement de l'apprentissage. Pour voir cela, calculons la dérivée partielle de la valeur avec entropie croisée en poids. Remplacez a = σ (z) dans (57), appliquez la règle de chaîne deux fois et obtenez

$$

$$\ frac {\ partial C} {\ partial w_j} = - \ frac {1} {n} \ sum_x \ left (\ frac {y} {\ sigma (z)} - \ frac {(1-y)} {1- \ sigma (z)} \ right) \ frac {\ partial \ sigma} {\ partial w_j} \ tag {58}$$

$$

$$= - \ frac {1} {n} \ sum_x \ left (\ frac {y} {\ sigma (z)} - \ frac {(1-y)} {1- \ sigma (z)} \ right) \ sigma '(z) x_j \ tag {59}$$

Réduisant à un dénominateur commun et simplifiant, on obtient:

$$

$$\ frac {\ partial C} {\ partial w_j} = \ frac {1} {n} \ sum_x \ frac {\ sigma '(z) x_j} {\ sigma (z) (1- \ sigma (z)) } (\ sigma (z) -y). \ tag {60}$$

En utilisant la définition de sigmoïde, σ (z) = 1 / (1 + e ^−z ) et un peu d'algèbre, nous pouvons montrer que σ ′ (z) = σ (z) (1 - σ (z)). Je vais vous demander de vérifier cela plus en détail dans l'exercice, mais pour l'instant, acceptez-le comme la vérité. Les termes σ (z) et σ (z) (1 - σ (z)) sont annulés, ce qui conduit à

$$

$$\ frac {\ partial C} {\ partial w_j} = \ frac {1} {n} \ sum_x x_j (\ sigma (z) -y). \ tag {61}$$

Grande expression. Il en résulte que la vitesse à laquelle les poids sont entraînés est contrôlée par σ (z) −y, c'est-à-dire par une erreur à la sortie. Plus l'erreur est grande, plus le neurone apprend vite. On pourrait s'y attendre intuitivement. Cette option évite le ralentissement de l'apprentissage provoqué par le terme σ '(z) dans une équation de coût quadratique similaire (55). Lorsque nous utilisons l'entropie croisée, le terme σ '(z) est réduit et nous n'avons plus à nous soucier de sa petitesse. Cette réduction est un miracle spécial garanti par la fonction de coût d'entropie croisée. En fait, bien sûr, ce n'est pas tout à fait un miracle. Comme nous le verrons plus loin, l'entropie croisée a été spécifiquement choisie pour cette propriété.

De même, la dérivée partielle du biais peut être calculée. Je ne donnerai pas tous les détails à nouveau, mais vous pouvez facilement vérifier que

$$

$$\ frac {\ partial C} {\ partial b} = \ frac {1} {n} \ sum_x (\ sigma (z) -y). \ tag {62}$$

Cela aide à nouveau à éviter un retard d'apprentissage dû au terme σ '(z) dans une équation similaire pour la valeur quadratique (56).

Exercice

• Vérifiez que σ ′ (z) = σ (z) (1 - σ (z)).

Revenons à notre exemple farfelu avec lequel nous avons joué plus tôt et voyons ce qui se passe si nous utilisons l'entropie croisée au lieu de la valeur quadratique. Pour syntoniser, nous commençons par le cas où le coût quadratique fonctionnait parfaitement lorsque le poids initial était de 0,6 et que le décalage était de 0,9. L'article d'origine a une forme interactive dans laquelle vous pouvez cliquer sur le bouton Exécuter et voir ce qui se passe lorsque vous remplacez la valeur quadratique par une entropie croisée.

Sans surprise, le neurone dans ce cas est parfaitement entraîné, comme auparavant. Examinons maintenant le cas dans lequel le neurone était coincé , avec un poids et un déplacement commençant à 2,0.



Succès! Cette fois, le neurone a appris rapidement, comme nous le voulions. Si vous regardez de plus près, vous pouvez voir que la pente de la courbe de coût est initialement plus raide par rapport à la région plate de la courbe de valeur quadratique correspondante. Cette entropie de cross-country nous donne cette fraîcheur, et elle ne nous laisse pas coincés là où nous nous attendons à l'entraînement le plus rapide d'un neurone quand il commence par de très grosses erreurs.

Je n'ai pas dit quelle vitesse d'entraînement a été utilisée dans les derniers exemples. Plus tôt, avec une valeur quadratique, nous avons utilisé η = 0,15. Faut-il utiliser la même vitesse dans les nouveaux exemples? En fait, en changeant la fonction de coût, il est impossible de dire exactement ce que signifie utiliser la «même» vitesse d'apprentissage; ce sera une comparaison des pommes avec des oranges. Pour les deux fonctions de coût, j'ai expérimenté en recherchant une vitesse d'apprentissage qui me permet de voir ce qui se passe. Si vous êtes toujours intéressé, alors dans les derniers exemples, η = 0,005.

Vous pouvez affirmer que la modification de la vitesse d'apprentissage rend les graphiques dénués de sens. Qui se soucie de la vitesse à laquelle un neurone apprend si nous pouvons choisir arbitrairement une vitesse d'apprentissage? Mais cette objection ne tient pas compte du point principal. La signification des graphiques n'est pas dans la vitesse absolue d'apprentissage, mais dans la façon dont cette vitesse change. Lors de l'utilisation de la fonction quadratique, l'entraînement est plus lent si le neurone est très mauvais, puis il va plus vite lorsque le neurone s'approche de la réponse souhaitée. Avec l'entropie croisée, l'apprentissage est plus rapide lorsqu'un neurone fait une grosse erreur. Et ces énoncés ne dépendent pas d'une vitesse d'apprentissage donnée.

Nous avons examiné l'entropie croisée pour un neurone. Cependant, cela est facile à généraliser aux réseaux avec de nombreuses couches et de nombreux neurones. Supposons que y = y ₁ , y ₂ , ... sont les valeurs souhaitées des neurones de sortie, c'est-à-dire les neurones de la dernière couche, et a ^L ₁ , a ^L ₂ , ... sont les valeurs de sortie elles-mêmes. L'entropie croisée peut alors être définie comme:

$$

$$C = - \ frac {1} {n} \ sum_x \ sum_j \ left [y_j \ ln a ^ L_j + (1-y_j) \ ln (1-a ^ L_j) \ right] \ tag {63}$$

C'est la même chose que l'équation (57), seulement maintenant notre ∑ _j somme sur tous les neurones de sortie. Je n'analyserai pas la dérivée en détail, mais il est raisonnable de supposer qu'en utilisant l'expression (63), nous pouvons éviter le ralentissement dans les réseaux avec de nombreux neurones. Si vous êtes intéressé, vous pouvez prendre le dérivé du problème ci-dessous.

Soit dit en passant, le terme «entropie croisée» que j'utilise a confondu certains des premiers lecteurs du livre, car il contredit d'autres sources. En particulier, souvent l'entropie croisée est déterminée pour deux distributions de probabilité, pj
et qj, comme ∑ _j p _j lnq _j . Cette définition peut être associée à (57), si l'on considère qu'un neurone sigmoïde donne une distribution de probabilité consistant en l'activation du neurone a et 1-a une valeur qui lui est complémentaire.

Cependant, si nous avons de nombreux neurones sigmoïdes dans la dernière couche, le vecteur a ^L _j ne donne généralement pas de distribution de probabilité. Par conséquent, la définition du type ∑ _j p _j lnq _{j n'a} pas de sens, car nous ne travaillons pas avec des distributions de probabilité. Au lieu de cela (63), on peut imaginer comment un ensemble sommé d'entropies croisées de chaque neurone est résumé, où l'activation de chaque neurone est interprétée comme faisant partie d'une distribution de probabilité à deux éléments (bien sûr, il n'y a aucun élément de probabilité dans nos réseaux, donc ce ne sont en fait pas des probabilités). En ce sens, (63) sera une généralisation de l'entropie croisée pour les distributions de probabilité.

Quand utiliser l'entropie croisée au lieu de la valeur quadratique? En fait, l'entropie croisée sera presque toujours mieux utilisée si vous avez des neurones de sortie sigmoïdes. Pour comprendre cela, n'oubliez pas que lors de la configuration d'un réseau, nous initialisons généralement des pondérations et des décalages à l'aide d'un processus aléatoire. Il peut arriver que ce choix conduise au fait que le réseau interprétera complètement certaines données d'entrée d'entraînement - par exemple, le neurone de sortie aura tendance à 1, alors qu'il devrait aller à 0, ou vice versa. Si nous utilisons une valeur quadratique qui ralentit l'entraînement, cela n'arrêtera pas du tout l'entraînement, car les poids continueront d'être entraînés sur d'autres exemples d'entraînement, mais cette situation n'est évidemment pas souhaitable.

Exercices

• Une prise de l'entropie croisée est qu'au début, il peut être difficile de se rappeler les rôles correspondants de y et a. Il est facile de se confondre, car ce sera correct, - [ylna + (1 - y) ln (1 - a)] ou - [alny + (1 - a) ln (1 - y)]. Qu'adviendra-t-il de la deuxième expression lorsque y = 0 ou 1? Ce problème affecte-t-il la première expression? Pourquoi?
• Dans la discussion d'un seul neurone au début de la section, j'ai dit que l'entropie croisée est petite si σ (z) ≈y pour toutes les données d'entrée d'entraînement. , y 0 1. , (, ) y 0 1. , , σ(z)=y . ,

  $$

  $$C = -\frac{1}{n} \sum_x [y \ln y+(1-y) \ln(1-y)] \tag{64}$$
  . −[ylny+(1−y)ln(1−y)] .

• . ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \sigma'(z^L_j) \tag{65}$$
  σ'(z ^L _j ) , . , δ ^L x

  $$

  $$\delta^L = a^L-y \tag{66}$$
  , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{67}$$
  σ'(z ^L _j ) , , , . . , .
• . , . , , , , a ^L _j = z ^L _j . , δL x

  $$

  $$\delta^L = a^L-y \tag{68}$$
  , , , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{69}$$

  $$

  $$\frac{\partial C}{\partial b^L_{j}} = \frac{1}{n} \sum_x (a^L_j-y_j) \tag{70}$$
  , , . .

MNIST

L'entropie croisée est facile à mettre en œuvre dans le cadre d'un programme qui enseigne le réseau en utilisant la descente de gradient et la propagation arrière. Nous le ferons plus tard en développant une version améliorée de notre premier programme de classification numérique manuscrite du MNIST, network.py. Le nouveau programme s'appelle network2.py et comprend non seulement l'entropie croisée, mais aussi plusieurs autres techniques développées dans ce chapitre. En attendant, voyons dans quelle mesure notre nouveau programme classe les chiffres MNIST. Comme au chapitre 1, nous utiliserons un réseau avec 30 neurones cachés et un mini-paquet de taille 10. Nous fixerons la vitesse d'apprentissage η = 0,5 et nous apprendrons 30 époques.

Comme je l'ai déjà dit, il est impossible de dire exactement quelle vitesse d'entraînement convient dans quel cas, j'ai donc expérimenté la sélection. Il est vrai qu'il existe un moyen de relier très approximativement de manière heuristique le taux d'apprentissage à l'entropie croisée et à la valeur quadratique. Nous avons vu plus haut que dans les termes du gradient de la valeur quadratique il y a un terme supplémentaire σ '= σ (1-σ). Supposons que nous faisons la moyenne de ces valeurs pour σ, ∫ ¹ ₀ dσ σ (1 - σ) = 1/6. On peut voir que le coût quadratique (très grossièrement) apprend en moyenne 6 fois plus lentement pour le même taux d'apprentissage. Cela suggère qu'un bon point de départ est de diviser la vitesse d'apprentissage d'une fonction quadratique par 6. Bien sûr, ce n'est pas du tout un argument strict, et vous ne devriez pas le prendre trop au sérieux. Mais cela peut parfois être utile comme point de départ.

L'interface de network2.py est légèrement différente de network.py, mais il devrait quand même être clair ce qui se passe. La documentation sur network2.py peut être obtenue en utilisant la commande help (network2.Network.SGD) dans le shell python.

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True) 

Notez, en passant, que la commande net.large_weight_initializer () est utilisée pour initialiser les poids et les décalages de la même manière que celle décrite dans le chapitre 1. Nous devons l'exécuter car nous changerons l'initialisation des poids par défaut plus tard. Par conséquent, après avoir démarré toutes les commandes ci-dessus, nous obtenons un réseau qui fonctionne avec une précision de 95,49%. Ceci est très proche du résultat du premier chapitre, 95,42%, en utilisant la valeur quadratique.

Examinons également le cas où nous utilisons 100 neurones cachés et entropie croisée, et laissons le reste inchangé. Dans ce cas, la précision est de 96,82%. Il s'agit d'une amélioration majeure par rapport aux résultats du premier chapitre, où nous avons atteint une précision de 96,59% en utilisant la valeur quadratique. Le changement peut sembler faible, mais pensez que l'erreur est passée de 3,41% à 3,18%. Autrement dit, nous avons éliminé environ 1/14 des erreurs. C'est plutôt bien.

Il est assez agréable que la fonction de coût d'entropie croisée nous donne des résultats similaires ou meilleurs par rapport à la valeur quadratique. Cependant, ils ne prouvent pas sans équivoque que l'entropie croisée est le meilleur choix. Le fait est que je n'ai pas du tout essayé de choisir des hyperparamètres - la vitesse d'entraînement, la taille du mini-package, etc. Afin de rendre l'amélioration plus convaincante, nous devons aborder correctement leur optimisation. Mais les résultats sont toujours inspirants, et nos calculs théoriques confirment que l'entropie croisée est un meilleur choix que la fonction de coût quadratique.

Dans cet esprit, tout ce chapitre et, en principe, le reste du livre seront passés en revue. Nous allons développer de nouvelles technologies, les tester et obtenir de "meilleurs résultats". Bien sûr, c'est bien que nous voyions ces améliorations. Mais les interpréter est toujours difficile. Cela ne sera convaincant que si nous constatons des améliorations après un travail sérieux sur l'optimisation de tous les autres hyperparamètres. Et c'est un travail assez compliqué, nécessitant de grandes ressources de calcul, et généralement nous ne traiterons pas une enquête aussi approfondie. Au lieu de cela, nous irons plus loin sur la base de tests informels, tels que ceux listés ci-dessus. Mais vous devez garder à l'esprit que ces tests ne sont pas des preuves sans ambiguïté et surveiller attentivement ces cas lorsque les arguments commencent à échouer.

Jusqu'à présent, nous avons discuté en détail de l'entropie croisée. Pourquoi gaspiller autant d'efforts si cela donne une si petite amélioration de nos résultats MNIST? Plus loin dans ce chapitre, nous verrons d'autres techniques - en particulier la régularisation - qui apportent des améliorations beaucoup plus fortes. Alors pourquoi nous concentrons-nous sur l'entropie croisée? En particulier, parce que l'entropie croisée est une fonction de valeur fréquemment utilisée, elle mérite donc une bonne compréhension. Mais la raison la plus importante est que la saturation des neurones est un problème important dans le domaine des réseaux de neurones, sur lequel nous reviendrons constamment tout au long du livre. Par conséquent, j'ai discuté de l'entropie croisée avec autant de détails, car c'est un bon laboratoire pour commencer à comprendre la saturation des neurones et comment aborder les approches de ce problème.

Que signifie l'entropie croisée? D'où cela vient-il?

Notre discussion sur l'entropie croisée a tourné autour de l'analyse algébrique et de la mise en œuvre pratique. C'est utile, mais en conséquence, des questions conceptuelles plus larges restent sans réponse, par exemple: que signifie l'entropie croisée? Existe-t-il un moyen intuitif de le présenter? Comment les gens pourraient-ils même trouver une entropie croisée?

Commençons par le dernier: qu'est-ce qui pourrait nous faire penser à l'entropie croisée? Supposons que nous ayons découvert un ralentissement de l'apprentissage décrit précédemment et réalisé qu'il était causé par les termes σ '(z) dans les équations (55) et (56). En jetant un petit coup d'œil sur ces équations, on pourrait se demander s'il est possible de choisir une telle fonction de coût pour que le terme σ '(z) disparaisse. Alors le coût C = C _{x d'} un exemple de formation satisferait les équations:

$$

$$\ frac {\ partial C} {\ partial w_j} = x_j (a-y) \ tag {71}$$

$$

$$\ frac {\ partial C} {\ partial b} = (a-y) \ tag {72}$$

Si nous choisissions une fonction de valeur qui les rend vraies, alors ils préfèrent simplement décrire une compréhension intuitive que plus l'erreur initiale est grande, plus le neurone apprend vite. Ils régleraient également le problème du ralentissement. En fait, à partir de ces équations, nous montrerions qu'il est possible de dériver la forme d'entropie croisée en suivant simplement un instinct mathématique. Pour voir cela, nous notons que, sur la base de la règle de chaîne, nous obtenons:

$$

$$\ frac {\ partial C} {\ partial b} = \ frac {\ partial C} {\ partial a} \ sigma '(z) \ tag {73}$$

En utilisant dans la dernière équation σ ′ (z) = σ (z) (1 - σ (z)) = a (1 - a), on obtient:

$$

$$\ frac {\ partial C} {\ partial b} = \ frac {\ partial C} {\ partial a} a (1-a) \ tag {74}$$

En comparant avec l'équation (72), nous obtenons:

$$

$$\ frac {\ partial C} {\ partial a} = \ frac {a-y} {a (1-a)} \ tag {75}$$

En intégrant cette expression sur a, on obtient:

$$

$$C = - [y \ ln a + (1-y) \ ln (1-a)] + {\ rm constant} \ tag {76}$$

Il s'agit de la contribution d'un exemple de formation distinct x à la fonction de coût. Pour obtenir la fonction de coût complet, nous devons faire la moyenne de tous les exemples de formation, et nous arrivons à:

$$

$$C = - \ frac {1} {n} \ sum_x [y \ ln a + (1-y) \ ln (1-a)] + {\ rm constant} \ tag {77}$$

La constante ici est la moyenne des constantes individuelles de chacun des exemples d'apprentissage. Comme vous pouvez le voir, les équations (71) et (72) déterminent uniquement la forme de l'entropie croisée, la chair à une constante commune. L'entropie croisée n'a pas été magiquement retirée de l'air mince. Elle pouvait être trouvée de manière simple et naturelle.

Qu'en est-il de l'idée intuitive de l'entropie croisée? Comment l'imagine-t-on? Une explication détaillée nous conduirait à dépasser notre stage. Cependant, nous pouvons mentionner l'existence d'une méthode standard d'interprétation de l'entropie croisée, issue du domaine de la théorie de l'information. En gros, l'entropie croisée est une mesure de surprise. Par exemple, notre neurone essaie de calculer la fonction x → y = y (x). Mais à la place, il compte la fonction x → a = a (x). Supposons que nous imaginions a comme une estimation du neurone de la probabilité que y = 1 et 1-a soit la probabilité que la valeur correcte pour y soit 0. Ensuite, l'entropie croisée mesure combien nous sommes «surpris», en moyenne, lorsque trouver la vraie valeur de y. Nous ne sommes pas très surpris si nous nous attendons à une sortie, et nous sommes très surpris si la sortie est inattendue. Bien sûr, je n'ai pas donné une définition stricte de "surprise", donc tout cela peut sembler une diatribe vide. Mais en fait, dans la théorie de l'information, il existe un moyen exact de déterminer l'inattendu. Malheureusement, je ne connais aucun exemple de discussion bonne, courte et autosuffisante sur ce point sur Internet. Mais si vous êtes intéressé à creuser un peu plus, l'article de Wikipédia contient de bonnes informations générales qui vous enverront dans la bonne direction. Les détails peuvent être trouvés dans le chapitre 5 sur les inégalités de Kraft dans un livre sur la théorie de l'information .

Défi

• Nous avons discuté en détail du ralentissement de l'apprentissage qui peut se produire lorsque les neurones sont saturés dans les réseaux utilisant la fonction de coût quadratique dans l'apprentissage. Un autre facteur qui peut inhiber l'apprentissage est la présence du terme x _j dans l'équation (61). De ce fait, lorsque la sortie x _j s'approche de zéro, le poids correspondant w _j sera entraîné lentement. Expliquez pourquoi il est impossible d'éliminer le terme x _{j en} choisissant une fonction de coût ingénieuse.

Softmax (fonction soft maximum)

Dans ce chapitre, nous utiliserons principalement la fonction de coût d'entropie croisée pour résoudre les problèmes de ralentissement de l'apprentissage. Cependant, je voudrais aborder brièvement une autre approche de ce problème, basée sur ce que l'on appelle couches softmax de neurones. Nous n'utiliserons pas de couches Softmax pour le reste de ce chapitre, donc si vous êtes pressé, vous pouvez ignorer cette section. Cependant, Softmax mérite encore d'être compris, en particulier parce qu'il est intéressant en soi, et en particulier parce que nous utiliserons les couches Softmax dans le chapitre 6, dans notre discussion sur les réseaux de neurones profonds.

L'idée de Softmax est de définir un nouveau type de couche de sortie pour HC. Elle commence de la même manière que la couche sigmoïde, avec la formation d'entrées pondérées $$$z ^ L_j = \ sum_ {k} w ^ L_ {jk} a ^ {L-1} _k + b ^ L_j$ . Cependant, nous n'utilisons pas de sigmoïde pour obtenir une réponse. Dans la couche Softmax, nous appliquons la fonction Softmax à z ^L _j . Selon elle, l'activation a ^L _{j du} neurone de sortie n ° j est égale à:

$$

$$a ^ L_j = \ frac {e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} \ tag {78}$$

où dans le dénominateur nous additionnons tous les neurones de sortie.

Si la fonction Softmax ne vous est pas familière, l'équation (78) vous semblera mystérieuse. Il n'est pas du tout évident pourquoi nous devrions utiliser une telle fonction. Il n'est pas non plus évident que cela nous aidera à résoudre le problème du ralentissement de l'apprentissage. Pour mieux comprendre l'équation (78), supposons que nous ayons un réseau avec quatre neurones de sortie et quatre entrées pondérées correspondantes, que nous désignerons comme z ^L ₁ , z ^L ₂ , z ^L ₃ et z ^L ₄ . L' article d'origine contient des curseurs de réglage interactifs, auxquels sont affectées les valeurs possibles des entrées pondérées et le calendrier des activations de sortie correspondantes. Un bon point de départ pour les étudier serait d'utiliser le curseur du bas pour augmenter z ^L ₄ .





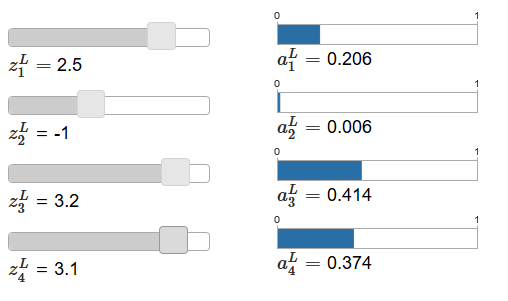
En augmentant z ^L ₄ , on peut observer une augmentation de l'activation de sortie correspondante, a ^L ₄ , et une diminution des autres activations de sortie. Avec une diminution de z ^L _4, ^{L L} diminuera et toutes les autres activations de sortie augmenteront. Après avoir regardé de près, vous verrez que dans les deux cas, le changement général dans d'autres activations compense exactement le changement qui se produit dans un ^L ₄ . La raison en est la garantie que toutes les activations de sortie donnent au total 1, ce que nous pouvons prouver en utilisant l'équation (78) et une certaine algèbre:

$$

$$\ sum_j a ^ L_j = \ frac {\ sum_j e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} = 1 \ tag {79}$$

Par conséquent, avec une augmentation de ^L _{4, les} activations de sortie restantes doivent diminuer de la même valeur au total pour garantir que la somme de toutes les activations de sortie soit égale à 1. Et, bien sûr, des déclarations similaires seront vraies pour toutes les autres activations.

Il résulte également de l'équation (78) que toutes les activations de sortie sont positives, car la fonction exponentielle est positive. En combinant cela avec l'observation de la section précédente, nous constatons que la sortie de la couche Softmax est un ensemble de nombres positifs donnant un total de 1. En d'autres termes, la sortie de la couche Softmax peut être représentée comme une distribution de probabilité.

Le fait que la sortie de la couche Softmax soit une distribution de probabilité est très agréable. Dans de nombreux problèmes, il est commode de pouvoir interpréter les activations de sortie a ^L _j comme une estimation par le réseau de la probabilité que le bulbe j soit la bonne option. Ainsi, par exemple, dans le problème de classification MNIST, nous pouvons interpréter un ^L _j comme une estimation par le réseau de la probabilité que j soit la version correcte de la classification d'un chiffre.

Inversement, si la couche de sortie était sigmoïde, nous ne pouvons certainement pas supposer que les activations forment une distribution de probabilité. Je ne le prouverai pas strictement, mais il est raisonnable de supposer que les activations de la couche sigmoïde dans le cas général ne forment pas une distribution de probabilité. Par conséquent, en utilisant une couche de sortie sigmoïde, nous n'obtiendrons pas une interprétation aussi simple des activations de sortie.

Exercice

• Faites un exemple montrant que dans un réseau avec une couche de sortie sigmoïde, les activations de sortie a ^L _j ne correspondent pas toujours à 1.

Nous commençons à comprendre un peu les fonctions Softmax et le comportement des couches Softmax. Pour résumer: les exposants de l'équation (78) garantissent que toutes les activations de sortie sont positives. La somme au dénominateur de l'équation (78) garantit que Softmax donne un total de 1. Par conséquent, ce type d'équation ne semble plus mystérieux: c'est un moyen naturel de s'assurer que les activations de sortie forment une distribution de probabilité. Softmax peut être imaginé comme un moyen de mettre à l'échelle z ^L _j , puis de les compresser ensemble pour former une distribution de probabilité.

Exercices

• La monotonie de Softmax. Montrer que ∂a ^L _j / ∂z ^L _{k est} positif si j = k, et négatif si j ≠ k. En conséquence, une augmentation de z ^L _{j est} garantie pour augmenter l'activation de sortie correspondante a ^L _j , et diminue toutes les autres activations de sortie. Nous l'avons déjà vu empiriquement en utilisant l'exemple des curseurs, mais cette preuve sera rigoureuse.
• Nonlocality Softmax. Une caractéristique intéressante des couches sigmoïdes est que la sortie a ^L _j est fonction de l'entrée pondérée correspondante, a ^L _j = σ (z ^L _j ). Expliquez pourquoi ce n'est pas le cas avec la couche Softmax: toute activation de sortie a ^L _j dépend de toutes les entrées pondérées.

Défi

• Inversez la couche Softmax. Supposons que nous ayons un NS avec une couche Softmax en sortie et que les activations a ^L _{j soient} connues. Montrer que les entrées pondérées correspondantes sont de la forme z ^L _j = ln a ^L _j + C, où C est une constante indépendante de j.

Problème de ralentissement de l'apprentissage

Nous nous sommes déjà familiarisés avec les couches de neurones Softmax. Mais jusqu'à présent, nous n'avons pas vu comment les couches Softmax nous permettent de résoudre le problème du ralentissement de l'apprentissage. Pour comprendre cela, définissons une fonction de coût basée sur la «log-vraisemblance». Nous utiliserons x pour désigner l'entrée d'apprentissage du réseau, et y pour la sortie souhaitée correspondante. Le LPS associé à cette entrée de formation sera alors:

$$

$$C \ equiv - \ ln a ^ L_y \ tag {80}$$

Donc, si, par exemple, nous étudions sur des images MNIST, et que l'image 7 est entrée dans l'entrée, alors le LPS sera −ln a ^L ₇ . Pour comprendre cela intuitivement, nous considérons le cas où le réseau résiste bien à la reconnaissance, c'est-à-dire qu'il est sûr qu'il est à l'entrée 7. Dans ce cas, il évaluera la valeur de la probabilité correspondante a ^L ₇ comme proche de 1, donc le coût −ln a ^L ₇ sera petit . Inversement, si le réseau ne fonctionne pas bien, alors la probabilité d'un ^L ₇ sera moindre, et le coût −ln d'un ^L ₇ sera plus. Par conséquent, le LPS se comporte comme prévu à partir d'une fonction de coût.

Et le problème du ralentissement? Pour l'analyser, nous rappelons que l'essentiel de la décélération est le comportement de ∂C / ∂w ^L _jk et ∂C / ∂b ^L _j . Je ne décrirai pas en détail la capture du dérivé - je vous demanderai de le faire dans les tâches, mais en utilisant une algèbre, vous pouvez montrer que:

$$

$$\ frac {\ partial C} {\ partial b ^ L_j} = a ^ L_j-y_j \ tag {81}$$

$$

$$\ frac {\ partial C} {\ partial w ^ L_ {jk}} = a ^ {L-1} _k (a ^ L_j-y_j) \ tag {82}$$

J'ai joué un peu avec la notation ici, et j'utilise «y» un peu différemment que dans le dernier paragraphe. Là, y désigne la sortie réseau souhaitée - c'est-à-dire, si la sortie est «7», alors l'entrée était l'image 7. Et dans ces équations, y désigne le vecteur d'activation de sortie correspondant à 7, c'est-à-dire un vecteur avec tous les zéros sauf l'unité en 7 e position.

Ces équations sont les mêmes que des expressions similaires que nous avons obtenues dans une analyse antérieure de l'entropie croisée. Comparez, par exemple, les équations (82) et (67). Il s'agit de la même équation, bien que cette dernière soit moyennée sur des exemples de formation. Et, comme dans le premier cas, ces expressions garantissent que l'apprentissage n'est pas ralenti. Il est utile d'imaginer que la couche de sortie Softmax avec LPS est assez similaire à la couche avec sortie sigmoïde et coût basé sur l'entropie croisée.

Compte tenu de leur similitude, que faut-il utiliser - sortie sigmoïde et entropie croisée, ou sortie Softmax et LPS? En fait, dans de nombreux cas, les deux approches fonctionnent bien. Bien que plus loin dans ce chapitre, nous utiliserons une couche de sortie sigmoïde avec un coût basé sur l'entropie croisée. Plus tard, au chapitre 6, nous utiliserons parfois la sortie Softmax et LPS. La raison de ces changements est de rendre certains des réseaux suivants plus similaires aux réseaux trouvés dans certains articles de recherche influents. D'un point de vue plus général, Softmax et LPS doivent être utilisés lorsque vous devez interpréter les activations de sortie comme des probabilités. Ce n'est pas toujours nécessaire, mais cela peut être utile dans les problèmes de classification (comme le MNIST), qui incluent des classes qui ne se croisent pas.

Les tâches

• Dérivez les équations (81) et (82).
• D'où vient le nom Softmax? Supposons que nous modifions la fonction Softmax de sorte que les activations de sortie soient données par l'équation

  $$

  $$a ^ L_j = \ frac {e ^ {c z ^ L_j}} {\ sum_k e ^ {c z ^ L_k}} \ tag {83}$$
  où c est une constante positive. Notez que c = 1 correspond à la fonction Softmax standard. Mais en utilisant une valeur différente de c, nous obtenons une autre fonction qui sera toujours qualitativement similaire à Softmax. Montrez que les activations de sortie forment une distribution de probabilité, comme c'est le cas avec Softmax normal. Supposons que nous rendions c très grand, c'est-à-dire c → & inf;. Quelle est la valeur limite des activations de sortie a ^L _j ? Après avoir résolu ce problème, il devrait être clair pourquoi une fonction avec c = 1 est considérée comme une «version adoucie» de la fonction maximale. C'est de là que vient le terme softmax.
• Propagation arrière avec Softmax et LPS. Dans le dernier chapitre, nous avons dérivé l'algorithme de rétropropagation pour un réseau contenant des couches sigmoïdes. Pour appliquer cet algorithme aux couches réseau et Softmax, nous devons dériver l'expression de l'erreur δ ^L _j ≡ ∂C / ∂z ^L _j . Montrer qu'une expression appropriée serait

  $$

  $$\ delta ^ L_j = a ^ L_j -y_j \ tag {84}$$
  En utilisant cette expression, nous pouvons appliquer l'algorithme de rétropropagation au réseau en utilisant la couche Softmax de sortie et le LPS.

Recyclage et régularisation

Le lauréat du prix Nobel Enrico Fermi a une fois été demandé un avis sur le modèle mathématique proposé par plusieurs collègues pour résoudre un important problème physique non résolu. Le modèle correspondait parfaitement à l'expérience, mais Fermi était sceptique à ce sujet. Il a demandé combien de paramètres libres pouvaient être modifiés. «Quatre», lui ont-ils dit. Fermi a répondu: "Je me souviens comment mon ami Johnny von Neumann aimait à dire qu'avec quatre paramètres, vous pouvez pousser un éléphant là-bas, et avec cinq, vous pouvez lui faire agiter sa trompe."

Le sens de l'histoire, bien sûr, est que les modèles avec un grand nombre de paramètres libres peuvent décrire une gamme étonnamment large de phénomènes.Même si un tel modèle fonctionne bien avec les données disponibles, il n'en fait pas automatiquement un bon modèle. Cela pourrait simplement signifier que le modèle a suffisamment de liberté pour décrire presque n'importe quel ensemble de données d'une taille donnée sans révéler l'idée principale du phénomène. Lorsque cela se produit, le modèle fonctionne bien avec les données existantes, mais ne peut pas généraliser la nouvelle situation. Un véritable test d'un modèle est sa capacité à faire des prédictions dans des situations qu'il n'a pas rencontrées auparavant.

Fermi et von Neumann se méfiaient des modèles à quatre paramètres. Notre NS avec 30 neurones cachés pour la classification des chiffres MNIST a près de 24 000 paramètres! Ce sont quelques paramètres. Notre NS avec 100 neurones cachés a près de 80 000 paramètres, et les NS profonds avancés de ces paramètres ont parfois des millions, voire des milliards. Pouvons-nous faire confiance aux résultats de leur travail?

Compliquons ce problème en créant une situation dans laquelle notre réseau généralise mal une nouvelle situation pour lui. Nous utiliserons NS avec 30 neurones cachés et 23 860 paramètres. Mais nous ne formerons pas le réseau avec les 50 000 images MNIST. Au lieu de cela, nous n'utilisons que le premier 1000. L'utilisation d'un ensemble limité rendra le problème de généralisation plus évident. Nous étudierons comme précédemment, en utilisant la fonction de coût basée sur l'entropie croisée, avec une vitesse d'apprentissage de η = 0,5 et une taille de mini-paquet de 10. Cependant, nous étudierons 400 époques, ce qui est légèrement plus qu'auparavant, car il existe des exemples de formation nous n'en avons pas beaucoup. Utilisons network2 pour voir comment la fonction de coût change:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True, monitor_training_cost=True) 

En utilisant les résultats, nous pouvons construire un graphique des changements de coûts lors de la formation du réseau (les graphiques ont été créés en utilisant le programme overfitting.py):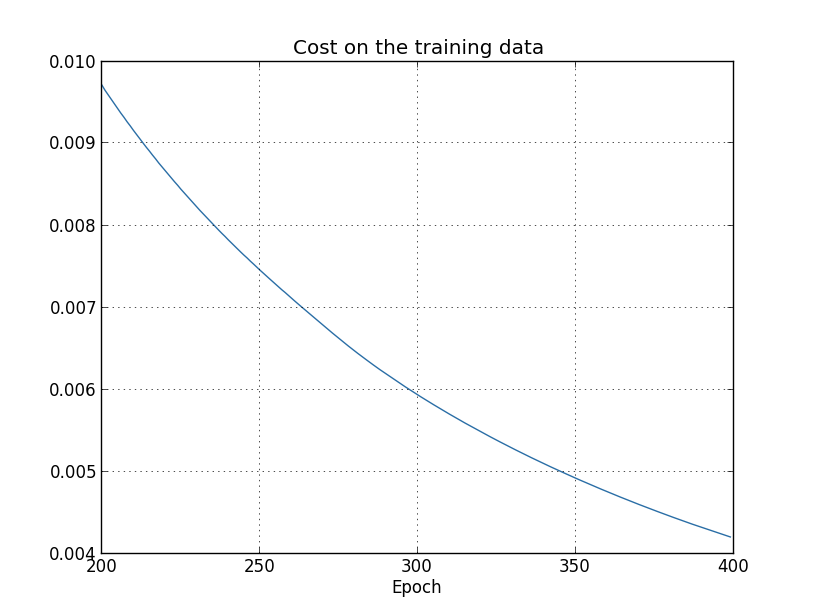



Cela semble encourageant, il y a une diminution régulière des coûts, comme prévu. Gardez à l'esprit que je n'ai montré que les époques de 200 à 399. En conséquence, nous voyons à une échelle agrandie les derniers stades de la formation, où, comme nous le verrons plus tard, tout ce qui se passe de plus intéressant.

Voyons maintenant comment la précision de la classification des données de vérification évolue au fil du temps:



Puis j'ai encore augmenté le calendrier. Au cours des 200 premières époques, qui ne sont pas visibles ici, la précision augmente à près de 82%. Ensuite, la formation ralentit progressivement. Enfin, vers la 280e ère, la précision de la classification cesse de s'améliorer. Aux époques ultérieures, seules de petites fluctuations stochastiques sont observées autour de la valeur de précision atteinte à la 280e époque. Comparez cela au graphique précédent, où le coût associé aux données de formation diminue progressivement. Si vous étudiez uniquement ce coût, il semblerait que le modèle s'améliore. Cependant, les résultats du travail avec les données de test nous indiquent que cette amélioration n'est qu'une illusion. Comme dans le modèle que Fermi n'aimait pas, ce que notre réseau étudie après la 280e ère n'est plus généralisé aux données de vérification. Par conséquent, cette formation cesse d'être utile. Nous disons qu'après la 280e ère, le réseau se reconstitue,ou sur-ajustement.

Vous vous demandez peut-être si ce n'est pas un problème que j'étudie les coûts en fonction des données de formation et non pas de l'exactitude de la classification des données de vérification. En d'autres termes, le problème est peut-être que nous comparons des pommes avec des oranges. Que se passera-t-il si nous comparons le coût des données de formation avec le coût de la vérification, c'est-à-dire que nous comparerons des mesures comparables? Ou peut-être pourrions-nous comparer l'exactitude de la classification des données de formation et de test? En fait, le même phénomène apparaît quelle que soit la façon dont la comparaison est effectuée. Mais les détails changent. Par exemple, voyons la valeur des données de vérification:



On peut voir que le coût des données de vérification s'améliore jusqu'aux environs de la 15e ère, puis commence à se détériorer complètement, bien que le coût des données de formation continue de s'améliorer. Ceci est un autre signe d'un modèle recyclé. Cependant, la question se pose: à quelle époque devrions-nous considérer le moment où le recyclage commence à prévaloir sur la formation - 15 ou 280? D'un point de vue pratique, nous souhaitons néanmoins améliorer l'exactitude de la classification des données de vérification, et le coût n'est qu'un médiateur de l'exactitude de la classification. Par conséquent, il est logique de considérer l'ère du 280 comme un point, après quoi le recyclage commence à prévaloir sur la formation de notre Assemblée nationale.

Un autre signe de reconversion est perceptible dans l'exactitude de la classification des données de formation:



La précision augmente, atteignant 100%. Autrement dit, notre réseau classe correctement les 1000 images d'entraînement! Pendant ce temps, la précision de la vérification atteint seulement 82,27%. Autrement dit, notre réseau étudie uniquement les fonctionnalités de l'ensemble de formation et n'apprend pas du tout à reconnaître les nombres. Il semble que le réseau se souvienne simplement de l'ensemble de formation, ne comprenant pas suffisamment les chiffres pour généraliser cela à l'ensemble de test.

La reconversion est un problème grave de l'Assemblée nationale. Cela est particulièrement vrai pour les NS modernes, qui ont généralement une énorme quantité de poids et de déplacements. Pour une formation efficace, nous avons besoin d'un moyen de déterminer quand le recyclage se produit afin de ne pas se recycler. Et nous aimerions également pouvoir réduire les effets de la reconversion.

Un moyen évident de détecter la reconversion consiste à utiliser l'approche ci-dessus, à surveiller la précision du travail avec les données de vérification pendant la formation du réseau. Si nous constatons que la précision des données de vérification ne s'améliore plus, nous devons arrêter la formation. Bien sûr, à proprement parler, ce ne sera pas nécessairement un signe de recyclage. Peut-être que la précision du travail avec les données de test et d'entraînement cessera de s'améliorer en même temps. Pourtant, l'application d'une telle stratégie empêchera le recyclage.

Et nous utiliserons une petite variation de cette stratégie. Rappelons que lorsque nous chargeons des données dans MNIST, nous les divisons en trois ensembles:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Jusqu'à présent, nous avons utilisé training_data et test_data, et ignoré validation_data [confirmation]. Validation_data contient 10 000 images, qui diffèrent à la fois de 50 000 images de l'ensemble de formation MNIST et de 10 000 images de l'ensemble de validation. Au lieu d'utiliser test_data pour éviter le sur-ajustement, nous utiliserons validation_data. Pour ce faire, nous utiliserons presque la même stratégie que celle décrite ci-dessus pour test_data. Autrement dit, nous calculerons la précision de classification de validation_data à la fin de chaque ère. Une fois que la précision de classification de validation_data est complète, nous arrêterons d'apprendre. Cette stratégie est appelée arrêt anticipé. Bien sûr, dans la pratique, nous ne pourrons pas découvrir immédiatement que la précision est rassasiée. Au lieu de cela, nous continuerons la formation jusqu'à ce que nous nous en assurions (et décidonsquand vous devez vous arrêter, ce n’est pas toujours facile, et vous pouvez utiliser des approches plus ou moins agressives pour cela).

Pourquoi utiliser validation_data pour empêcher le recyclage plutôt que test_data? Cela fait partie d'une stratégie plus générale d'utiliser validation_data pour évaluer différents choix d'hyperparamètres - le nombre d'époques à apprendre, la vitesse d'apprentissage, la meilleure architecture de réseau, etc. Nous utilisons ces estimations pour trouver et attribuer de bonnes valeurs aux hyperparamètres. Et même si je ne l'ai pas encore mentionné, c'est en partie à cause de cela que j'ai fait le choix des hyperparamètres dans les exemples précédents du livre.

Bien sûr, cette remarque ne répond pas à la question de savoir pourquoi nous utilisons validation_data, et non test_data, pour éviter le sur-ajustement. Il remplace simplement la réponse à une question plus générale - pourquoi utilisons-nous validation_data, et non test_data, pour sélectionner des hyperparamètres? Pour comprendre cela, gardez à l'esprit que lors du choix des hyperparamètres, nous devons très probablement choisir parmi une variété de leurs options. Si nous attribuons des hyperparamètres basés sur les évaluations de test_data, nous adapterons probablement trop ces données spécifiquement pour test_data. Autrement dit, nous pouvons trouver des hyperparamètres qui sont bien adaptés aux caractéristiques spécifiques de données spécifiques de test_data, cependant, le fonctionnement de notre réseau ne sera pas généralisé à d'autres ensembles de données. Nous évitons cela en sélectionnant des hyperparamètres à l'aide de validation_data. Et puis, après avoir reçu le GP dont nous avons besoin,nous effectuons une évaluation finale de la précision en utilisant test_data. Cela nous donne la certitude que nos résultats avec test_data sont une vraie mesure du degré de généralisation de la NS. En d'autres termes, les données de support sont des données de formation spéciales qui nous aident à apprendre un bon médecin généraliste. Cette approche de localisation des généralistes est parfois appelée méthode de rétention, car validation_data est "conservé" séparément de training_data.

En pratique, même après avoir évalué la qualité du travail sur test_data, nous voudrons changer d'avis et essayer une approche différente - peut-être une architecture réseau différente - qui inclura des recherches pour un nouvel ensemble de GPs. Dans ce cas, existe-t-il un risque que nous nous adaptions inutilement à test_data? Aurons-nous besoin d'un nombre potentiellement infini d'ensembles de données afin d'être sûrs que nos résultats sont bien généralisés? En général, il s'agit d'un problème profond et complexe. Mais pour nos besoins pratiques, nous ne nous en préoccuperons pas trop. Nous plongons simplement tête baissée dans de nouvelles recherches en utilisant une méthode de rétention simple basée sur training_data, validation_data et test_data, comme décrit ci-dessus.

Jusqu'à présent, nous avons envisagé de recycler en utilisant 1000 images d'entraînement. Que se passe-t-il si nous utilisons un ensemble de formation complet de 50 000 images? Nous laisserons tous les autres paramètres inchangés (30 neurones cachés, vitesse d'apprentissage 0,5, taille de mini-paquet 10), mais nous étudierons 30 époques en utilisant les 50 000 images. Voici un graphique qui montre la précision de la classification sur les données d'entraînement et les données de test. Notez qu'ici, j'ai utilisé des données de validation plutôt que des données de validation pour faciliter la comparaison des résultats avec les graphiques précédents.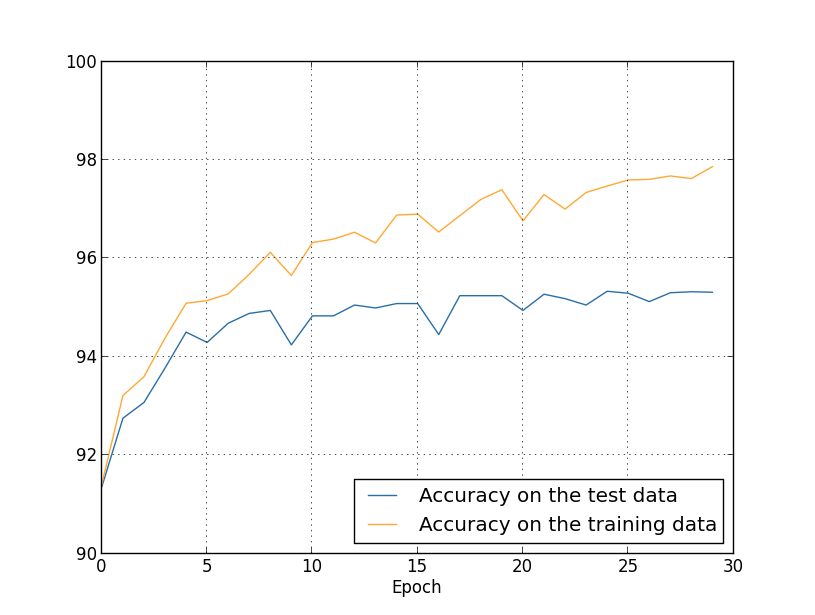



On peut voir que les indicateurs de précision sur les données de test et de formation restent plus proches les uns des autres que lors de l'utilisation de 1000 exemples de formation. En particulier, la meilleure précision de classification, 97,86%, n'est que de 2,53% supérieure à 95,33% des données de vérification. Comparez avec une pause anticipée de 17,73%! Un recyclage est en cours, mais considérablement réduit. Notre réseau compile beaucoup mieux les informations, passant de la formation aux données de test. En général, l'un des meilleurs moyens de réduire le recyclage est d'augmenter la quantité de données de formation. Avec suffisamment de données de formation, il est difficile de recycler même un très grand réseau. Malheureusement, l'obtention des données d'entraînement est coûteuse et / ou difficile, donc cette option n'est pas toujours pratique.

Régularisation

Augmenter la quantité de données de formation est un moyen de réduire le recyclage. Existe-t-il d'autres moyens de réduire le recyclage? Une approche possible consiste à réduire la taille du réseau. Certes, les grands réseaux ont plus de potentiel que les petits, nous sommes donc réticents à recourir à cette option.

Heureusement, il existe d'autres techniques qui peuvent réduire le recyclage, même lorsque nous avons fixé la taille du réseau et les données de formation. Ils sont connus comme des techniques de régularisation. Dans ce chapitre, je décrirai l'une des techniques les plus populaires, parfois appelées affaiblissement des poids ou régularisation de L2. Son idée est d'ajouter un membre supplémentaire appelé membre de régularisation à la fonction de coût. Voici l'entropie croisée avec régularisation:

$$

$$C = -\frac{1}{n} \sum_{xj} \left[ y_j \ln a^L_j+(1-y_j) \ln (1-a^L_j)\right] + \frac{\lambda}{2n} \sum_w w^2 \tag{85}$$

Le premier terme est une expression courante pour l'entropie croisée. Mais nous en avons ajouté une seconde, à savoir la somme des carrés de tous les poids du réseau. Il est mis à l'échelle par le facteur λ / 2n, où λ> 0 est le paramètre de régularisation et n, comme d'habitude, est la taille de l'ensemble d'apprentissage. Nous verrons comment choisir λ. Il convient également de noter que le terme de régularisation ne comprend pas les biais. À ce sujet ci-dessous.

Bien sûr, il est possible de régulariser d'autres fonctions de coût, par exemple quadratique. Cela peut être fait d'une manière similaire:

$$

$$C = \frac{1}{2n} \sum_x \|y-a^L\|^2 + \frac{\lambda}{2n} \sum_w w^2 \tag{86}$$

Dans les deux cas, nous pouvons écrire la fonction de coût régularisé comme

$$

$$C = C_0 + \frac{\lambda}{2n} \sum_w w^2 \tag{87}$$

où C ₀ est la fonction de coût d'origine sans régularisation.

Il est intuitivement clair que le point de régularisation est d'incliner le réseau pour préférer des poids plus petits, toutes choses égales par ailleurs. Des poids importants ne seront possibles que s'ils améliorent considérablement la première partie de la fonction de coût. En d'autres termes, la régularisation est une façon de choisir un compromis entre trouver de petits poids et minimiser la fonction de coût initial. Il est important que ces deux éléments du compromis dépendent de la valeur de λ: lorsque λ est petit, nous préférons minimiser la fonction de coût d'origine, et lorsque λ est grand, nous préférons les petits poids.

Il n'est pas du tout évident que le choix d'un tel compromis devrait contribuer à réduire la reconversion! Mais il s'avère que cela aide. Nous découvrirons pourquoi cela aide dans la section suivante. Mais d'abord, travaillons avec un exemple montrant que la régularisation réduit effectivement le recyclage.

Pour construire un exemple, nous devons d'abord comprendre comment appliquer l'algorithme d'apprentissage avec descente de gradient stochastique à un NS régularisé. En particulier, nous devons savoir comment calculer les dérivées partielles, ∂C / ∂w et ∂C / ∂b pour tous les poids et décalages du réseau. Après avoir pris les dérivées partielles dans l'équation (87), nous obtenons:

$$

$$\frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} w \tag{88}$$

$$

$$\frac{\partial C}{\partial b} = \frac{\partial C_0}{\partial b} \tag{89}$$

Les termes ∂C ₀ / ∂w et ∂C ₀ / ∂w peuvent être calculés via l'OP, comme décrit dans le chapitre précédent. Nous voyons qu'il est facile de calculer le gradient de la fonction de coût régularisé: il suffit d'utiliser OP comme d'habitude, puis d'ajouter λ / nw à la dérivée partielle de tous les termes de pondération. Les dérivées partielles par rapport aux déplacements ne changent pas, donc, la règle d'apprentissage par descente de gradient pour les déplacements ne diffère pas de l'habituelle:

$$

$$b \rightarrow b -\eta \frac{\partial C_0}{\partial b} \tag{90}$$

La règle d'entraînement pour les poids se transforme en:

$$

$$w \rightarrow w-\eta \frac{\partial C_0}{\partial w}-\frac{\eta \lambda}{n} w \tag{91}$$

$$

$$= \left(1-\frac{\eta \lambda}{n}\right) w -\eta \frac{\partial C_0}{\partial w} \tag{92}$$

Tout est le même que dans la règle de descente de gradient habituelle, sauf que nous modifions d'abord le poids w par un facteur de 1 - ηλ / n. Cette mise à l'échelle est parfois appelée perte de poids, car elle réduit le poids. À première vue, il semble que les poids tendent irrésistiblement vers zéro. Mais ce n'est pas le cas, car l'autre terme peut conduire à une augmentation des poids s'il conduit à une diminution de la fonction de coût irrégulier.

Ok, laissez la descente en pente fonctionner comme ça. Qu'en est-il de la descente de gradient stochastique? Eh bien, comme dans la version irrégulière de la descente de gradient stochastique, nous pouvons estimer ∂C ₀ / ∂w en faisant la moyenne sur le mini-package de m exemples d'entraînement. Par conséquent, la règle d'apprentissage régularisée pour la descente de gradient stochastique devient (voir équation (20)):

$$

$$w \rightarrow \left(1-\frac{\eta \lambda}{n}\right) w -\frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial w} \tag{93}$$

où la somme va pour les exemples de formation x dans le mini-package, et C _x est le coût irrégulier pour chaque exemple de formation. Tout est le même que dans la règle habituelle de descente de gradient stochastique, à l'exception de 1 - ηλ / n, le facteur de perte de poids. Enfin, pour compléter l'image, permettez-moi d'écrire une règle régularisée pour les compensations. Naturellement, c'est exactement la même chose que dans le cas irrégulier (voir équation (21)):

$$

$$b \rightarrow b - \frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial b} \tag{94}$$

où va le montant pour les exemples de formation x dans le mini-package.

Voyons comment la régularisation modifie l'efficacité de notre Assemblée nationale. Nous utiliserons un réseau avec 30 neurones cachés, un mini-paquet de taille 10, une vitesse d'apprentissage de 0,5 et une fonction de coût avec entropie croisée. Cependant, cette fois, nous utilisons le paramètre de régularisation λ = 0,1. Dans le code, j'ai nommé cette variable lmbda, car le mot lambda est réservé en python pour des choses qui ne sont pas liées à notre sujet. J'ai également utilisé à nouveau test_data au lieu de validation_data. Mais j'ai décidé d'utiliser test_data, car les résultats peuvent être comparés directement avec nos premiers résultats irréguliers. Vous pouvez facilement modifier le code afin qu'il utilise validation_data et vous assurer que les résultats sont similaires.

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, ... evaluation_data=test_data, lmbda = 0.1, ... monitor_evaluation_cost=True, monitor_evaluation_accuracy=True, ... monitor_training_cost=True, monitor_training_accuracy=True) 

Le coût des données de formation diminue constamment, comme dans le premier cas, sans régularisation:



mais cette fois, la précision sur test_data continue d'augmenter tout au long des 400 époques: de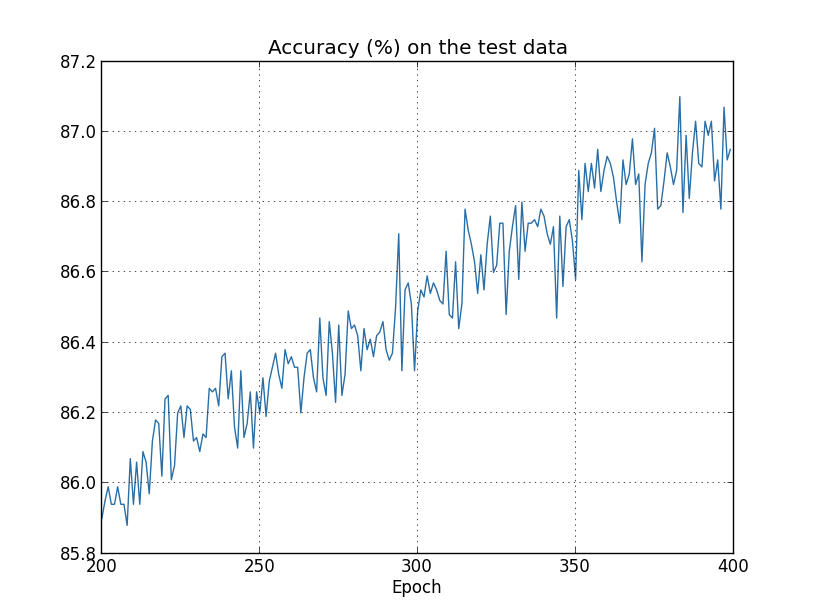



toute évidence, la régularisation a supprimé la reconversion. De plus, la précision a considérablement augmenté et la précision de classification des pics atteint 87,1%, contre 82,27% atteint dans le cas sans régularisation. En général, nous obtenons presque certainement de meilleurs résultats en continuant à étudier après 400 époques. Empiriquement, la régularisation semble permettre à notre réseau de mieux généraliser les connaissances et de réduire considérablement les effets de la reconversion.

Que se passe-t-il si nous quittons notre environnement artificiel, qui n'utilise que 1 000 images pédagogiques, et retournons à l'ensemble complet de 50 000 images? Bien sûr, nous avons déjà vu que le recyclage est un problème beaucoup plus petit avec un ensemble complet de 50 000 images. La régularisation contribue-t-elle à améliorer le résultat? Gardons les valeurs précédentes des hyperparamètres - 30 époques, vitesse 0,5, taille de mini-paquet 10. Cependant, nous devons changer le paramètre de régularisation. Le fait est que la taille n de l'ensemble d'apprentissage est passée de 1000 à 50 000, ce qui modifie le facteur d'affaiblissement des poids 1 - ηλ / n. Si nous continuons à utiliser λ = 0,1, cela signifierait que les poids sont beaucoup moins affaiblis et, par conséquent, l'effet de la régularisation diminue. Nous compensons cela en acceptant λ = 5,0.

Ok, formons notre réseau en réinitialisant d'abord les poids:

 >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, ... evaluation_data=test_data, lmbda = 5.0, ... monitor_evaluation_accuracy=True, monitor_training_accuracy=True) 

Nous obtenons les résultats: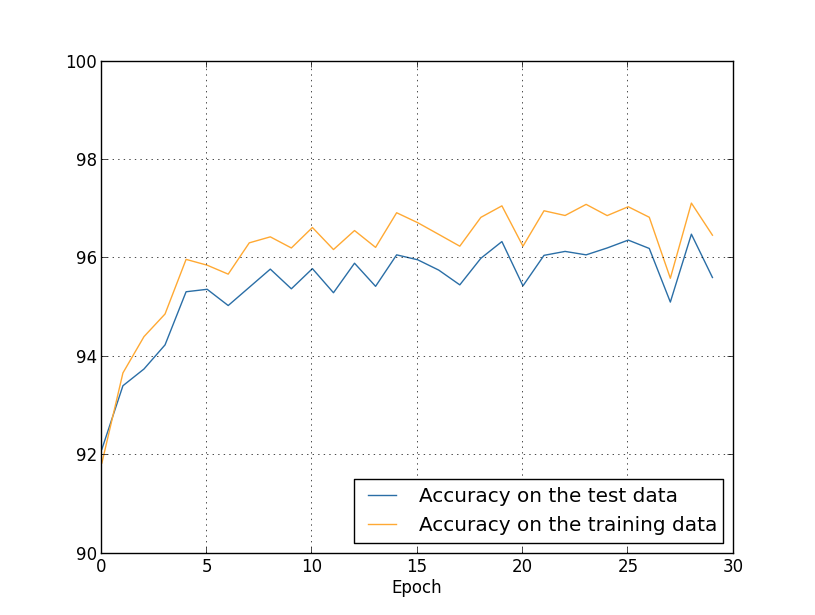



beaucoup de choses agréables. Premièrement, notre précision de classification sur les données de vérification est passée de 95,49% sans régularisation à 96,49% avec régularisation. Il s'agit d'une amélioration majeure. Deuxièmement, on peut voir que l'écart entre les résultats des travaux sur les ensembles de formation et de test est beaucoup plus faible qu'auparavant, moins de 1%. L'écart est encore décent, mais nous avons manifestement fait des progrès importants dans la réduction du recyclage.

Enfin, voyez quelle précision de classification nous obtenons en utilisant 100 neurones cachés et le paramètre de régularisation & lambda = 5.0. Je ne donnerai pas une analyse détaillée de la reconversion, c'est juste pour le plaisir, pour voir combien de précision peut être obtenue avec nos nouvelles astuces: une fonction de coût avec entropie croisée et régularisation de L2.

 >>> net = network2.Network([784, 100, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, lmbda=5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

– 97,92% . 30 . , 60 η=0,1 λ=5,0, 98%, 98,04 . 152 !

. . , MNIST, , , «», , . . , , .

Pourquoi en est-il ainsi? Heureusement, lorsque la fonction de coût n'a pas de régularisation, la longueur du vecteur de pondérations augmentera très probablement, toutes choses étant égales par ailleurs. Au fil du temps, cela peut conduire à un très grand vecteur de poids. Et à cause de cela, le vecteur des écailles peut se coincer, montrant approximativement dans la même direction, car les changements dus à la descente du gradient ne font que de minuscules changements de direction avec une grande longueur du vecteur. Je crois qu'en raison de ce phénomène, il est très difficile pour notre algorithme de formation d'étudier correctement l'espace des poids, et donc il est difficile de trouver un bon minimum de la fonction de coût.