Bruit dans les mégadonnées. Analyse d'entropie

Je suis tombé sur une tâche appelée Enscombe Quartet ( Anscombe ) »( version anglaise ).

La figure 1 montre une distribution tabulaire de 4 fonctions aléatoires (tirée de Wikipedia).


Fig. 1. Tableau de distribution de quatre fonctions aléatoires

La figure 2 montre les paramètres de distribution de ces fonctions aléatoires


Fig. 2. Paramètres de distribution de quatre fonctions aléatoires

Et leurs graphiques dans la figure 3.


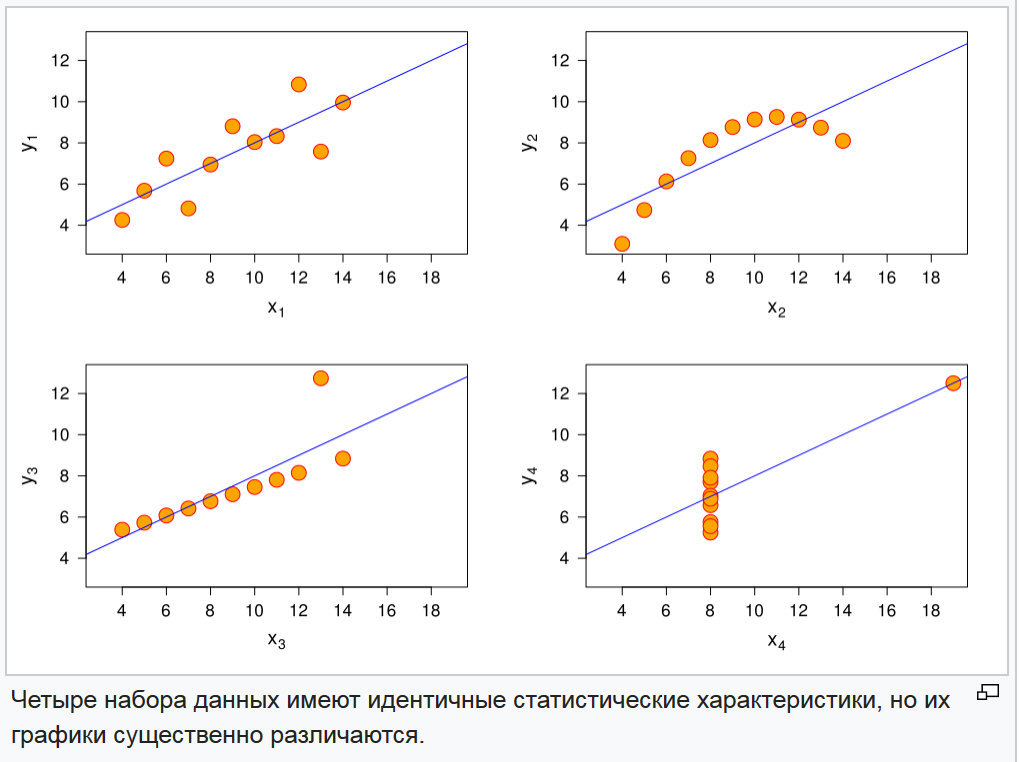Fig. 3. Graphiques de quatre fonctions aléatoires

Le problème de la distinction de ces fonctions est résolu tout simplement en comparant les moments des ordres supérieurs et leurs indicateurs normalisés: coefficient d' asymétrie et coefficient d' excès . Ces indicateurs sont présentés dans la figure 4.


Fig. 4. Indicateurs des moments des troisième et quatrième ordres et l'asymétrie et les coefficients excédentaires de quatre fonctions aléatoires

Comme le montre le tableau de la figure 4, la combinaison de ces indicateurs pour toutes les fonctions est différente.
La première conclusion, qui suggère naturellement que les informations sur les positions relatives des points sont stockées dans les paramètres de distribution à un niveau supérieur à la variance de la distribution aléatoire.

De nombreux analystes tentent d'isoler des équations de régression particulières dans les mégadonnées et jusqu'à présent, il s'agit aujourd'hui d'une méthode de sélection de l'équation avec la plus petite dispersion résiduelle. Il n'y avait pas grand-chose à ajouter. Mais j'ai attiré l'attention sur le fait que ce sont toutes des informations, et les informations ont un indicateur d' entropie . Et elle, l'entropie, a ses limites à partir de 0, lorsque l'information est complètement déterminée au bruit blanc. Et le bruit blanc dans le canal de transmission a une distribution uniforme.

Lorsqu'il est nécessaire d'analyser les données, il est initialement supposé qu'elles contiennent des données connexes qui doivent être formalisées en tant que relation. Et cela suggère que les données ne sont pas du bruit blanc. C'est-à-dire que la première étape est la sélection de l'équation de régression et la détermination de la variance résiduelle. Si la régression est choisie correctement, la variance résiduelle obéira à la loi de la distribution normale. Voyons et, dans les figures 5-7, les formules d'entropie pour une variable aléatoire uniformément distribuée et normalement distribuée sont présentées.



Fig. 5. La formule de l'entropie différentielle pour une quantité normalement distribuée (VV Afanasyev. Théorie des probabilités dans les questions et les tâches . Ministère de l'éducation et des sciences de la Fédération de Russie Université pédagogique d'État de Yaroslavl du nom de K. D. Ushinsky)


Fig. 6. La formule d'entropie différentielle pour une quantité normalement distribuée (Pugachev VS La théorie des fonctions aléatoires et son application aux problèmes de contrôle automatique . Ed. 2nd, révisé et complété. - M.: Fizmatlit, 1960. - 883 p.)


Fig. 7. La formule de l'entropie différentielle pour une quantité uniformément distribuée (Pugachev VS La théorie des fonctions aléatoires et son application aux problèmes de contrôle automatique . Ed. 2nd, révisé et complété. - M.: Fizmatlit, 1960. - 883 p.)

Ensuite, nous montrons un exemple. Mais nous prenons d'abord les conditions que chacune des quatre fonctions est la coordonnée de l'hyperplan, c'est-à-dire que nous vérifions en même temps le fonctionnement du modèle dans l'espace multidimensionnel. Dessinez une convolution d'un hypercube sur un plan. Le mécanisme est présenté à la figure 8.




Fig. 8. Données initiales avec le mécanisme de convolution


Fig. 9. Regroupement agrégé sur la figure.


Fig. 10. Paramètres de distribution de quatre fonctions aléatoires et un regroupement récapitulatif.

Considérez le mécanisme de choix de la taille de l'intervalle de partition. Les conditions initiales sont présentées dans la figure 11.


Fig. 11. Les conditions initiales de la division en intervalles.

Condition 1. Elle doit être avec une probabilité non nulle sur la région de variation, car sinon, l'entropie est égale à l'infini. Tant pour l'échantillon initial que pour le résidu.

Condition 2. Comme il est impossible d'ignorer la possibilité d'une valeur aberrante dans les nouvelles données, etc., pour les intervalles extrêmes, il est nécessaire d'établir la probabilité selon la loi théorique normale ou autre généralement acceptée de distribution de probabilité, selon le principe de la probabilité de queues.

Condition 3. L'étape d'intervalle doit fournir le nombre minimal requis d'intervalles sur la répartition de l'échantillon résiduel.

Condition 4. Le nombre d'intervalles doit être impair.

Condition 5. Le nombre d'intervalles doit garantir un accord fiable avec la loi théorique de distribution choisie pour l'étude.


Fig. 12. Le reste de la distribution

Définissez le mécanisme de sélection d'intervalle dans la figure 13.


Fig. 13. L'algorithme de sélection d'intervalle

Le principal problème, à mon avis, était de décider d'introduire ou non des intervalles de queue. Si pour la dispersion résiduelle, cela semblait assez naturel, alors pour la série principale, c'est assez tendu.


Fig. 14. Les résultats du traitement des valeurs des données pour déterminer l'entropie de l'information

Conclusions Où cet outil peut-il être appliqué

En comparant les indicateurs résultants du tableau de la figure 14, on peut voir qu'ils ont réagi au changement dans la structure des données. Et cela signifie que l'outil a une sensibilité, et vous permet de résoudre des problèmes similaires à la tâche du quatuor Enskomb.

Sans aucun doute, ces problèmes peuvent être résolus à l'aide de moments d'ordre supérieur. Mais à la base, l'entropie informationnelle dépend de la variance d'une variable aléatoire, c'est-à-dire qu'il s'agit d'une caractéristique tierce de la variance. Ainsi, nous pouvons indiquer les intervalles où l'utilisation de l'analyse de la variance peut conduire à un résultat spécifique.

La caractéristique numérique de l'entropie permet de réaliser une analyse de corrélation avec des variables indépendantes. À titre d'exemple de manifestation d'une connexion possible, voici ce qui suit: Supposons que, sur l'intervalle de a à b, le niveau de bruit d'une série de données augmente, en comparant les valeurs des variables indépendantes, nous avons constaté que la variable xn est entrée dans la plage de plus de 5 unités, après variable, diminué en dessous de +5, le bruit a diminué. De plus, un contrôle supplémentaire peut être effectué et, si cette hypothèse est confirmée, alors dans d'autres études, interdire à la variable xn de dépasser +5. Puisque dans ce cas, les données deviennent inutiles.

Je suppose qu'il existe d'autres options pour utiliser cet outil.

Comment utiliser

Sous cet aspect, le mécanisme naturel de la «moyenne mobile» est examiné, je suppose que la taille d'échantillon obtenue par la formule de taille d'échantillon à partir d'une analyse statistique donnera un volume raisonnable de la zone de glissement. Selon l'analyse actuelle, il a été conclu que la taille de l'échantillon devrait être déterminée à partir de la proportion minimale qui tombe sur la moindre probabilité. Dans notre exemple, pour la variance résiduelle, la fraction minimale de l'intervalle empirique est de 0,15909. Cela doit être fait, car si un intervalle dans le volume de glissement s'avère vide, alors dans ce cas, le chiffre de bruit sera scandaleux ou la règle fonctionnera que le logarithme de 0 est égal à moins l'infini. Et avec une taille d'échantillon correctement sélectionnée, les valeurs transcendantales de cet indicateur indiqueront un changement cardinal dans la structure de l'information.