Un certain nombre de mes collègues sont confrontés au problème que pour calculer une sorte de métrique, par exemple le taux de conversion, vous devez valider la base de données entière. Ou vous devez effectuer une étude détaillée pour chaque client, où il y a des millions de clients. Ce type de kerry peut fonctionner pendant un certain temps, même dans des référentiels spécialement conçus. Ce n'est pas très amusant d'attendre 5 à 15 à 40 minutes jusqu'à ce qu'une simple mesure soit considérée pour découvrir que vous devez calculer autre chose ou ajouter autre chose.
L'échantillonnage est une solution à ce problème: nous n'essayons pas de calculer notre métrique sur l'ensemble du tableau de données, mais prenons un sous-ensemble qui représente de manière représentative les métriques dont nous avons besoin. Cet échantillon peut être 1000 fois plus petit que notre tableau de données, mais il est assez bon pour montrer les chiffres dont nous avons besoin.
Dans cet article, j'ai décidé de montrer comment l'échantillonnage de la taille des échantillons affecte l'erreur de métrique finale.
Le problème
La question clé est: dans quelle mesure l'échantillon décrit-il bien la «population»? Puisque nous prenons un échantillon d'un tableau commun, les métriques que nous recevons se révèlent être des variables aléatoires. Différents échantillons nous donneront des résultats métriques différents. Différent, cela ne veut pas dire du tout. La théorie des probabilités nous dit que les valeurs métriques obtenues par échantillonnage doivent être regroupées autour de la vraie valeur métrique (faite sur l'ensemble de l'échantillon) avec un certain niveau d'erreur. De plus, nous avons souvent des problèmes où un niveau d'erreur différent peut être supprimé. C'est une chose de déterminer si nous obtenons une conversion de 50% ou 10%, et c'est une autre chose d'obtenir un résultat avec une précision de 50,01% contre 50,02%.
Il est intéressant de noter que du point de vue de la théorie, le coefficient de conversion observé par nous sur l'ensemble de l'échantillon est également une variable aléatoire, car Le taux de conversion «théorique» ne peut être calculé que sur un échantillon de taille infinie. Cela signifie que même toutes nos observations dans la base de données donnent en fait une estimation de conversion avec leur précision, bien qu'il nous semble que ces nombres calculés sont absolument exacts. Cela conduit également à la conclusion que même si aujourd'hui le taux de conversion diffère d'hier, cela ne signifie pas que quelque chose a changé, mais signifie seulement que l'échantillon actuel (toutes les observations dans la base de données) provient de la population générale (tout est possible). observations pour ce jour, qui se sont produites et n’ont pas eu lieu) ont donné un résultat légèrement différent d’hier. En tout cas, pour tout produit ou analyste honnête, cela devrait être une hypothèse de base.
Disons que nous avons 1 000 000 d'enregistrements dans une base de données de type 0/1, qui nous indiquent si une conversion s'est produite lors d'un événement. Le taux de conversion est alors simplement la somme de 1 divisé par 1 million.
Question: si nous prenons un échantillon de taille N, dans quelle mesure et avec quelle probabilité le taux de conversion sera-t-il différent de celui calculé sur l'ensemble de l'échantillon?
Considérations théoriques
La tâche se réduit à calculer l'intervalle de confiance du coefficient de conversion pour un échantillon d'une taille donnée pour une distribution binomiale.
D'après la théorie, l'écart type pour la distribution binomiale est:
S = sqrt (p * (1 - p) / N)
O Where
p - taux de conversion
N - Taille de l'échantillon
S - écart type
Je ne considérerai pas l'intervalle de confiance direct de la théorie. Il y a un matan assez compliqué et déroutant, qui relie en fin de compte l'écart type et l'estimation finale de l'intervalle de confiance.
Développons une "intuition" sur la formule d'écart type:
- Plus la taille de l'échantillon est grande, plus l'erreur est petite. Dans ce cas, l'erreur tombe dans la dépendance quadratique inverse, c'est-à-dire augmenter l'échantillon de 4 fois n'augmente la précision que de 2 fois. Cela signifie qu'à un certain point, l'augmentation de la taille de l'échantillon ne donnera aucun avantage particulier et signifie également qu'une précision assez élevée peut être obtenue avec un échantillon assez petit.

- Il y a une dépendance de l'erreur sur la valeur du taux de conversion. L'erreur relative (c'est-à-dire le rapport de l'erreur à la valeur du taux de conversion) a une tendance "vile" à être plus grande, plus le taux de conversion est faible:
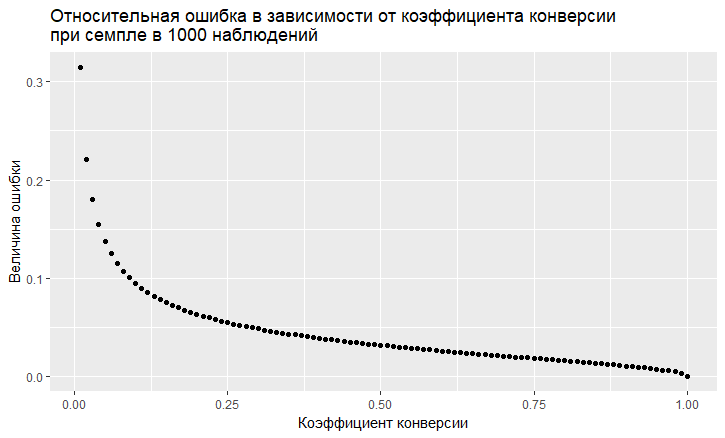
- Comme on le voit, l'erreur "s'envole" dans le ciel avec un faible taux de conversion. Cela signifie que si vous échantillonnez des événements rares, vous avez besoin de grands échantillons, sinon vous obtiendrez une estimation de conversion avec une très grosse erreur.
Modélisation
Nous pouvons complètement nous éloigner de la solution théorique et résoudre le problème "de front". Grâce au langage R, c'est maintenant très facile à faire. Pour répondre à la question, quelle erreur obtenons-nous lors de l'échantillonnage, vous pouvez simplement faire un millier d'échantillons et voir quelle erreur nous obtenons.
L'approche est la suivante:
- Nous prenons différents taux de conversion (de 0,01% à 50%).
- Nous prenons 1000 échantillons de 10, 100, 1000, 10000, 50 000, 100 000, 250 000, 500 000 éléments dans l'échantillon
- Nous calculons le taux de conversion pour chaque groupe d'échantillons (1000 coefficients)
- Nous construisons un histogramme pour chaque groupe d'échantillons et déterminons dans quelle mesure se situent 60%, 80% et 90% des taux de conversion observés.
Code R générant des données:
sample.size <- c(10, 100, 1000, 10000, 50000, 100000, 250000, 500000) bootstrap = 1000 Error <- NULL len = 1000000 for (prob in c(0.0001, 0.001, 0.01, 0.1, 0.5)){ CRsub <- data.table(sample_size = 0, CR = 0) v1 = seq(1,len) v2 = rbinom(len, 1, prob) set = data.table(index = v1, conv = v2) print(paste('probability is: ', prob)) for (j in 1:length(sample.size)){ for(i in 1:bootstrap){ ss <- sample.size[j] subset <- set[round(runif(ss, min = 1, max = len),0),] CRsample <- sum(subset$conv)/dim(subset)[1] CRsub <- rbind(CRsub, data.table(sample_size = ss, CR = CRsample)) } print(paste('sample size is:', sample.size[j])) q <- quantile(CRsub[sample_size == ss, CR], probs = c(0.05,0.1, 0.2, 0.8, 0.9, 0.95)) Error <- rbind(Error, cbind(prob,ss,t(q))) }
En conséquence, nous obtenons le tableau suivant (il y aura des graphiques plus tard, mais les détails sont mieux visibles dans le tableau).
Voyons les cas avec une conversion de 10% et une faible conversion de 0,01%, car toutes les caractéristiques du travail avec l'échantillonnage y sont clairement visibles.
À 10% de conversion, l'image semble assez simple:

Les points sont les bords de l'intervalle de confiance de 5 à 95%, c'est-à-dire en faisant un échantillon, nous obtiendrons dans 90% des cas CR sur l'échantillon dans cet intervalle. Échelle verticale - taille de l'échantillon (échelle logarithmique), horizontale - valeur du coefficient de conversion. La barre verticale est un «vrai» CR.
Nous voyons la même chose que nous avons vu dans le modèle théorique: la précision augmente à mesure que la taille de l'échantillon augmente, et l'on converge assez rapidement et l'échantillon obtient un résultat proche de "vrai". Au total, pour 1000 échantillons, nous avons 8,6% - 11,7%, ce qui sera suffisant pour un certain nombre de tâches. Et dans 10 mille déjà 9,5% - 10,55%.
Les choses sont pires avec des événements rares et cela est conforme à la théorie:

Un faible taux de conversion de 0,01% pose des problèmes avec les statistiques de 1 million d'observations, et la situation avec les échantillons est encore pire. L'erreur est juste gigantesque. Sur des échantillons jusqu'à 10 000, la métrique n'est, en principe, pas valide. Par exemple, sur un échantillon de 10 observations, mon générateur vient d'obtenir 0 conversion 1000 fois, il n'y a donc qu'un point. À 100000, nous avons un écart de 0,005% à 0,0016%, c'est-à-dire que nous pouvons faire près de la moitié du coefficient avec un tel échantillonnage.
Il convient également de noter que lorsque vous observez une conversion d'une si petite échelle à 1 million d'essais, vous avez simplement une grosse erreur naturelle. Il en résulte que des conclusions sur la dynamique de ces événements rares doivent être tirées sur de très gros échantillons, sinon vous poursuivez simplement après les fantômes, les fluctuations aléatoires des données.
Conclusions:
- Échantillonnage d'une méthode de travail pour obtenir des estimations
- La précision de l'échantillon augmente avec l'augmentation de la taille de l'échantillon et diminue avec une diminution du taux de conversion.
- La précision des estimations peut être modélisée pour votre tâche et ainsi choisir l'échantillonnage optimal pour vous-même.
- Il est important de se rappeler que les événements rares ne sont pas bien échantillonnés
- En général, les événements rares sont difficiles à analyser; ils nécessitent de grands échantillons de données sans échantillons.