Convertissez l'image en son - qu'entendez-vous?

Salut Habr.

Une publication récente ici sur le site décrit un appareil qui permet aux aveugles de «voir» une image, la transformant à l'aide d'ondes sonores. D'un point de vue technique, dans cet article, il n'y avait aucun détail (et si l'idée d'un million était volée ), mais le concept lui-même semblait intéressant. Ayant une certaine expérience du traitement du signal, j'ai décidé d'expérimenter par moi-même.



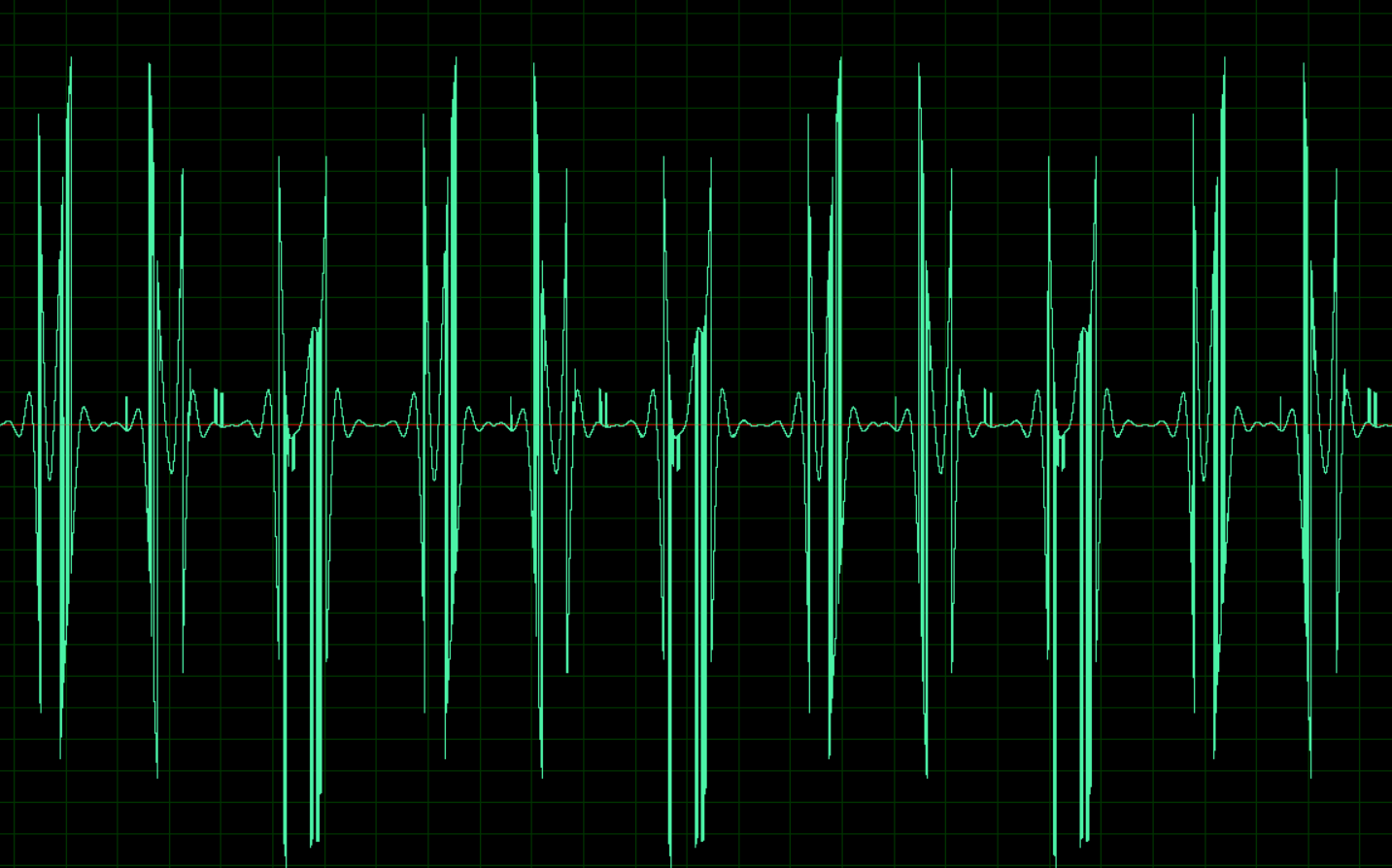
Ce qui en est sorti, détails et exemples de fichiers sous le chat.

Convertir 2D en 1D

La première tâche évidente qui nous attend est de convertir une image "plate" bidimensionnelle en une onde sonore "unidimensionnelle". Comme suggéré dans les commentaires sur cet article, il est pratique d'utiliser la courbe de Hilbert pour cela.

Il est essentiellement similaire à une fractale, et l'idée est qu'avec une augmentation de la résolution de l'image, la position relative des objets ne change pas (si l'objet était dans le coin supérieur gauche de l'image, il y restera ). Différentes dimensions des courbes de Hilbert peuvent nous donner des images différentes: 32x32 pour N = 5, 64x64 pour N = 6, etc. En «parcourant» l'image le long de cette courbe, nous obtenons une ligne, un objet unidimensionnel.

La question suivante est la taille de l'image. Je veux intuitivement prendre une image plus grande, mais il y a un grand «mais»: même l'image est 512x512, elle est 262144 pixels. Si nous convertissons chaque point en une impulsion audio, alors à une fréquence d'échantillonnage de 44100, nous obtenons une séquence de 6 secondes, ce qui est trop long - les images doivent être mises à jour rapidement, par exemple à l'aide d'une caméra Web. Cela n'a aucun sens d'augmenter la fréquence d'échantillonnage; nous obtenons des fréquences ultrasoniques qui sont inaudibles par l'oreille (bien que cela puisse fonctionner pour un hibou ou une chauve-souris). En conséquence, une résolution de 128x128 a été choisie par la méthode de piquer scientifique , qui donnera des impulsions de 0,37c de long - d'une part, il est assez rapide pour naviguer en temps réel, d'autre part, il suffit d'attraper tout changement de forme du signal à l'oreille.

Traitement d'image

La première étape consiste à télécharger l'image, à la convertir en n / b et à la mettre à l'échelle à la taille souhaitée. La taille de l'image dépend de la dimension de la courbe de Hilbert.

from PIL import Image from hilbertcurve.hilbertcurve import HilbertCurve import numpy as np from scipy.signal import butter, filtfilt # Create Hilbert curve dimension = 7 hilbert = HilbertCurve(dimension, n=2) print("Hilbert curve dimension:", dimension) # Maximum distance along curve print("Max_dist:", hilbert.max_h) # Maximum distance along curve print("Max_coord:", hilbert.max_x) # Maximum coordinate value in any dimension # Load PIL image f_name = "image01.png" img = Image.open(f_name) width, height = img.size out_size = hilbert_curve.max_x + 1 if width != out_size: img = img.resize((out_size, out_size), Image.ANTIALIAS) # Get image as grayscale numpy array img_grayscale = img.convert(mode='L') img_data = np.array(img_grayscale) 

L'étape suivante consiste à former une onde sonore. Ici, bien sûr, il peut y avoir un grand nombre d'algorithmes et de savoir-faire, pour le test, je viens de prendre le composant de luminosité. Bien sûr, il existe probablement de meilleures façons.

 width, height = img_grayscale.size sound_data = np.zeros(width*height) for ii in range(width*height): coord_x, coord_y = hilbert_curve.coordinates_from_distance(ii) pixel_l = img_data[coord_x][coord_y] # Inverse colors (paper-like, white = 0, black = 255) pixel_l = 255 - pixel_l # Adjust values 0..255 to 0..8192 ampl = pixel_l*32 sound_data[ii] = ampl 

D'après le code, j'espère que tout est clair. La fonction coordonnées_de_distance fait tout le travail pour nous sur la conversion des coordonnées (x, y) en distance sur une courbe de Hilbert, nous inversons et convertissons la valeur de luminosité L en couleur.

Ce n'est pas tout. Parce que il peut y avoir de grands blocs de la même couleur dans l'image, cela peut conduire à l'apparition d'une «composante continue» dans le son - une longue série de valeurs non nulles, par exemple [100,100,100, ...]. Pour les supprimer, nous appliquons un filtre passe-haut (filtre Butterworth ) à notre réseau avec une fréquence de coupure de 50 Hz (la coïncidence avec la fréquence du réseau est aléatoire). Il y a une synthèse de filtres dans la bibliothèque scipy, que nous utiliserons.

 def butter_highpass(cutoff, fs, order=5): nyq = 0.5 * fs normal_cutoff = cutoff / nyq b, a = butter(order, normal_cutoff, btype='high', analog=False) return b, a def butter_highpass_filter(data, cutoff, fs, order=5): b, a = butter_highpass(cutoff, fs, order) y = filtfilt(b, a, data) return y # Apply high pass filter to remove dc component cutoff_hz = 50 sample_rate = 44100 order = 5 wav_data = butter_highpass_filter(sound_data, cutoff_hz, sample_rate, order) 

La dernière étape consiste à enregistrer l'image. Parce que la durée d'une impulsion est courte, nous la répétons 10 fois, elle sera plus audible au plus près d'une image réelle qui se répète, par exemple à partir d'une webcam.

 # Clip data to int16 range sound_output = np.clip(wav_data, -32000, 32000).astype(np.int16) # Save repeat = 10 sound_output_ntimes = np.tile(sound_output, repeat) wav_name = "ouput.wav" scipy.io.wavfile.write(wav_name, sample_rate, sound_output_ntimes) 

Résultats

L'algorithme ci-dessus est, bien sûr, assez primitif. Je voulais vérifier trois points - combien vous pouvez distinguer entre différentes formes simples et combien vous pouvez estimer la distance aux formes.

Test 1



L'image correspond au signal sonore suivant:


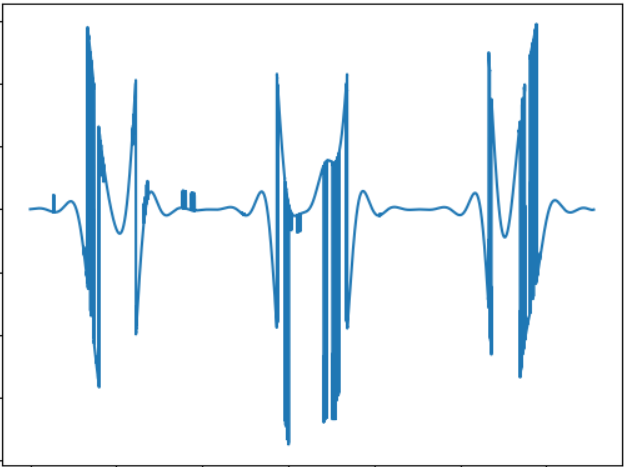
WAV: cloud.mail.ru/public/nt2R/2kwBvyRup

Test 2



L'idée de ce test est de comparer le «son» d'un objet de forme différente. Signal sonore:


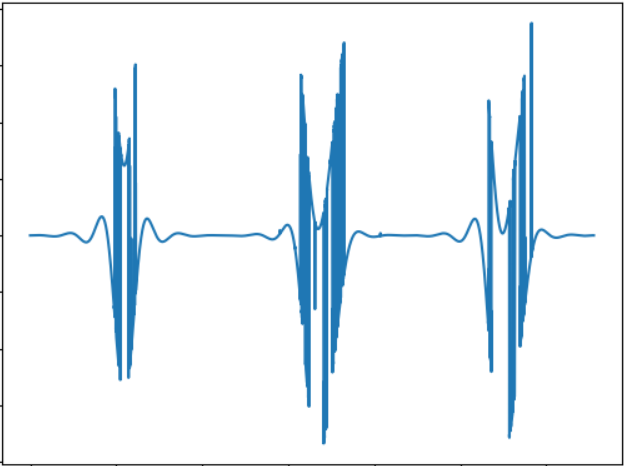
WAV: cloud.mail.ru/public/2rLu/4fCNRxCG2

Vous remarquerez peut-être que le son est vraiment différent et qu'il y a une différence à l'oreille.

Test 3



L'idée du test est de tester un objet plus petit. Signal sonore:


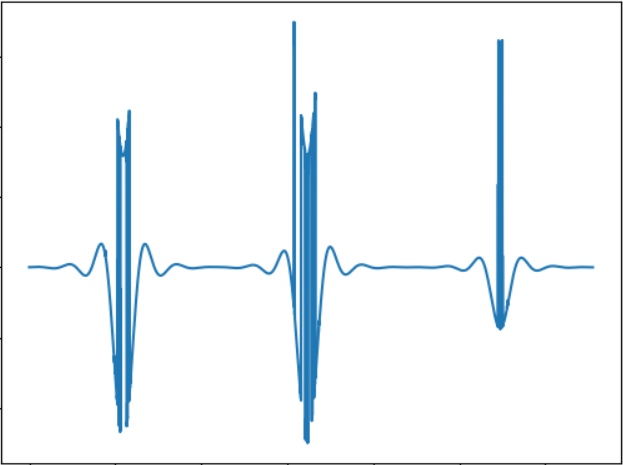
WAV: cloud.mail.ru/public/5GLV/2HoCHvoaY

En principe, plus la taille de l'objet est petite, moins il y aura de "rafales" dans le son, donc la dépendance ici est assez directe.

Modifier:

Comme suggéré dans les commentaires, vous pouvez utiliser la transformée de Fourier pour convertir directement les images en son. Un test rapide effectué montre les résultats suivants (les images sont les mêmes):
Test 1: cloud.mail.ru/public/2C5Z/5MEQ8Swjo
Test 2: cloud.mail.ru/public/2dxp/3sz8mjAib
Test 3: cloud.mail.ru/public/3NjJ/ZYrfdTYrk

Les tests semblent intéressants, au moins pour les petits et les grands carrés (fichiers 1 et 3), la différence d'audition est notable. Mais la forme des figures (1 et 2) ne diffère pratiquement pas, il y a donc aussi quelque chose à penser. Mais en général, le son obtenu en FFT, à l'oreille me plaît plus.

Conclusion

Ce test, bien sûr, n'est pas une thèse, mais simplement une preuve de concept, faite en quelques heures de temps libre. Mais même ainsi, cela fonctionne essentiellement, et il est tout à fait possible de ressentir la différence à l'oreille. Je ne sais pas s’il est possible d’apprendre à naviguer dans l’espace avec de tels sons, probablement, après un certain entraînement. Bien qu'il existe un vaste champ d'améliorations et d'expériences, par exemple, vous pouvez utiliser le son stéréo, ce qui vous permettra de mieux séparer les objets de différents côtés, vous pouvez expérimenter d'autres méthodes de conversion d'images en son, par exemple, coder la couleur à différentes fréquences, etc. Enfin, c'est prometteur l'utilisation de caméras 3D capables de percevoir la profondeur (hélas, une telle caméra n'est pas disponible). À propos, à l'aide d'un simple code OpenCV, l'algorithme ci-dessus peut être adapté pour utiliser une caméra Web, ce qui vous permettra d'expérimenter avec des images dynamiques.

Eh bien, comme d'habitude, toutes les expériences réussies.