Algorithme cryptographique Grasshopper: à peu près le complexe

Cet article détaillera l'algorithme de chiffrement de bloc défini dans GOST R 34.12-2015 comme Grasshopper. Sur quoi est-il basé, quelles sont les mathématiques des algorithmes de chiffrement par blocs et comment cet algorithme est implémenté en java.

Qui, comment, quand et pourquoi a développé cet algorithme restera en dehors du champ d'application de l'article, car dans ce cas, nous avons peu d'intérêt, sauf:

Sauterelle = Kuznetsov, Nechaev AND Company.



Étant donné que la cryptographie est principalement basée sur les mathématiques, de sorte qu'une explication supplémentaire ne pose pas beaucoup de questions, vous devez d'abord analyser les concepts de base et les fonctions mathématiques sur lesquels cet algorithme est construit.

Champs Galois

L'arithmétique des champs de Galois est une arithmétique polynomiale, c'est-à-dire que chaque élément de ce champ est un polynôme. Le résultat de toute opération est également un élément de ce champ. Un champ de Galois particulier se compose d'une plage fixe de nombres. La caractéristique de champ est appelée un nombre premier p. Ordre sur le terrain, c'est-à-dire la quantité de ses éléments est un certain degré naturel de caractéristique $$$p ^ m$ , où m ϵ N. Pour m = 1, le champ est appelé simple. Dans les cas où m> 1, pour la formation d'un champ, un polynôme générateur de degré m est également requis; un tel champ est appelé étendu. $$$Gf (p ^ m)$ - désignation du champ Galois. Le polynôme générateur est irréductible, c'est-à-dire simple (par analogie avec les nombres premiers, il est divisible par 1 et par lui-même sans reste). Puisque travailler avec n'importe quelle information, c'est travailler avec des octets, et qu'un octet fait 8 bits, prenez comme champ $$$Gf (2 ^ 8)$ et le polynôme générateur:

$$

$$x ^ 8 + x ^ 7 + x ^ 6 + x + 1.$$

Cependant, pour commencer, nous analyserons les opérations de base dans un domaine plus simple $$$Gf (2 ^ 3)$ avec génération d'un polynôme $$$f (x) = x ^ 3 + x + 1$ .

Opération d'addition

La plus simple est l'opération d'addition, qui dans l'arithmétique du champ de Galois est un simple module d'addition au niveau du bit 2 (R).

J'attire immédiatement l'attention sur le fait que le signe "+" ici et ci-après se réfère au fonctionnement de XOR au niveau du bit, et non à l'addition sous la forme habituelle.

La table de vérité de la fonction HOR



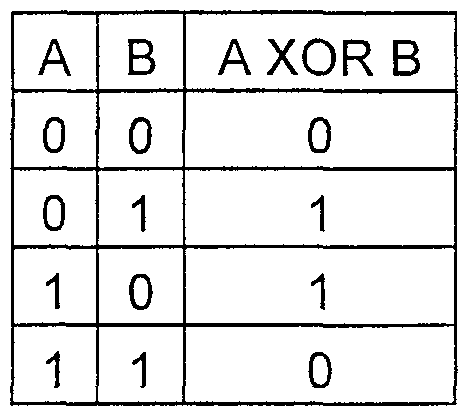
Un exemple: $$

Sous forme polynomiale, cette opération ressemblera à

$$

$$(x ^ 2 + 1) + (x + 1) = x ^ 2 + x = 110_2 = 6_ {10}$$

Opération de multiplication

Pour effectuer l'opération de multiplication, il est nécessaire de convertir les nombres sous forme polynomiale:

$$

Comme vous pouvez le voir, le nombre sous forme polynomiale est un polynôme dont les coefficients sont les valeurs des chiffres dans la représentation binaire du nombre.

Multipliez deux nombres sous forme polynomiale:

$$

$$

$$= x ^ 4 + x ^ 3 + x + 1 = 11011_2 = 27_ {10}$$

Le résultat de multiplication 27 n'est pas dans le champ utilisé. $$$Gf (2 ^ 3)$ (il se compose de chiffres de 0 à 7, comme mentionné ci-dessus). Pour lutter contre ce problème, il est nécessaire d'utiliser un polynôme générateur.

On suppose également que x satisfait l'équation $$$f (x) = x ^ 3 + x + 1 = 0$ alors



Faisons une table de multiplication:



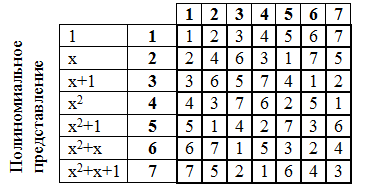
Le tableau des degrés des éléments du champ de Galois est d'une grande importance. L'augmentation à une puissance est également réalisée sous forme polynomiale, similaire à la multiplication.

Un exemple:

$$

$$

$$= x (x ^ 3 + x + 1) + x ^ 2 + x + 1 = x ^ 2 + x + 1 = 111_2 = 7_ {10}$$

Ainsi, nous compilons un tableau de degrés:



La table des degrés est cyclique: le septième degré correspond à zéro, donc le huitième correspond au premier, etc. Vous pouvez vérifier cela si vous le souhaitez.

Dans les champs de Galois, il y a le concept d'un terme primitif - un élément d'un champ dont les degrés contiennent tous les éléments non nuls du champ. On voit que tous les éléments correspondent à cette condition (enfin, sauf 1, naturellement). Mais ce n'est pas toujours le cas.

Pour les champs que nous considérons, c'est-à-dire avec la caractéristique 2, choisissez toujours 2. En tant que membre primitif, étant donné sa propriété, tout élément du champ peut être exprimé en termes de degré du membre primitif.



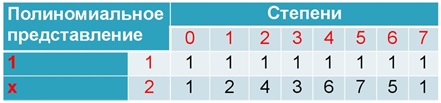
Un exemple: $$

En utilisant cette propriété, et en tenant compte de la cyclicité de la table des degrés, nous allons essayer de multiplier à nouveau les nombres:

$$

Le résultat coïncidait avec ce que nous avions calculé plus tôt.

Faisons maintenant la division:

$$

Le résultat obtenu est également vrai.

Eh bien, par souci d'exhaustivité, regardons élever à un pouvoir:

$$

Une telle approche de la multiplication et de la division est beaucoup plus simple que les opérations réelles utilisant des polynômes, et pour eux, il n'est pas nécessaire de stocker une grande table de multiplication, mais juste une rangée de degrés d'un membre de champ primitif.

Revenons maintenant à notre domaine $$$Gf (2 ^ 8)$

L'élément zéro du champ est un, le 1er est un deux, chaque élément suivant du 2e au 254e élément est calculé comme le précédent, multiplié par 2, et si l'élément est en dehors du champ, c'est-à-dire que sa valeur est supérieure à $$$(2 ^ 8-1)$ alors XOR se fait avec le nombre $$$195_ {10}$ , ce nombre représente le polynôme irréductible du champ $$$x ^ 8 + x ^ 7 + x ^ 6 + x + 1 = 2 ^ 8 + 2 ^ 7 ++ 2 ^ 6 + 2 + 1 = 451$ , nous apportons ce numéro sur le terrain $$ . Et le 255e élément est à nouveau 1. Nous avons donc un champ contenant 256 éléments, c'est-à-dire un ensemble complet d'octets, et nous avons analysé les opérations de base qui sont effectuées dans ce champ.



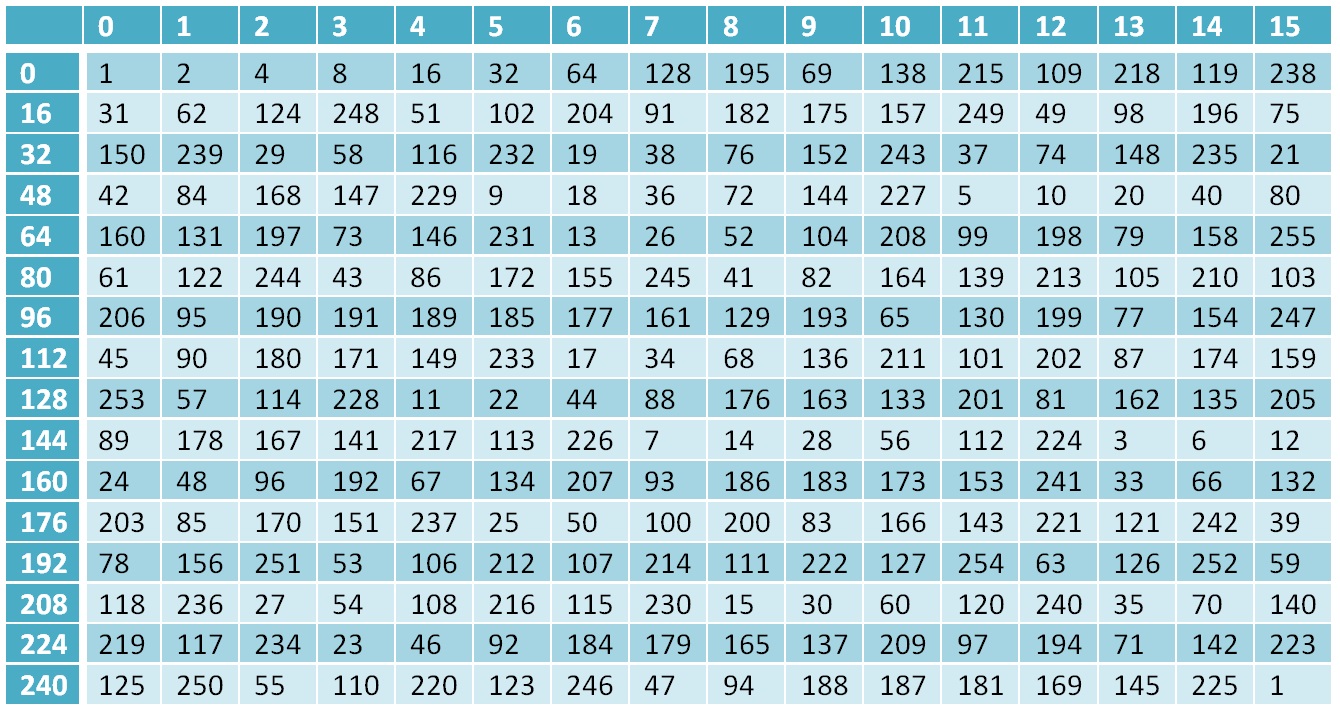
Tableau des puissances de deux pour le terrain $$$Gf (2 ^ 8)$

Pourquoi était-il nécessaire - une partie des calculs de l'algorithme Grasshopper est effectuée dans le champ Galois, et les résultats des calculs, respectivement, sont des éléments de ce champ.

Réseau Feistel

Feistel Network est une méthode de chiffrement par blocs développée par Horst Feistel chez IBM en 1971. Aujourd'hui, le réseau de Feistel est à la base d'un grand nombre de protocoles cryptographiques.

Le réseau Feistel fonctionne avec des blocs en texte clair:

1. Le bloc est divisé en deux parties égales - gauche L et droite R.
2. Le sous-bloc gauche L est modifié par la fonction f à l'aide de la touche K: X = f (L, K). En fonction, il peut y avoir n'importe quelle transformation.
3. Le sous-bloc X résultant est ajouté modulo 2 avec le sous-bloc droit R, qui reste inchangé: X = X + R.
4. Les pièces résultantes sont échangées et collées.

Cette séquence d'actions est appelée cellule Feistel.


Figure 1. Cellule Feistel

Le réseau Feistel est composé de plusieurs cellules. Les sous-blocs obtenus en sortie de la première cellule vont à l'entrée de la deuxième cellule, les sous-blocs résultants de la deuxième cellule vont à l'entrée de la troisième cellule, et ainsi de suite.

Algorithme de chiffrement

Maintenant, nous nous sommes familiarisés avec les opérations utilisées et pouvons passer au sujet principal - à savoir, le cryptoalgorithme Grasshopper.

La base de l'algorithme est le réseau dit SP - réseau de substitution-permutation. Le chiffrement basé sur le réseau SP reçoit un bloc et une clé en entrée et effectue plusieurs tours alternés constitués d'étages de substitution et d'étages de permutation. Grasshopper effectue neuf tours complets, chacun comprenant trois opérations consécutives:

1. L'opération d'application d'une clé ronde ou XOR au niveau du bit d'une clé et d'un bloc de données d'entrée;
2. Conversion non linéaire, qui est un simple remplacement d'un octet par un autre conformément au tableau;
3. Transformation linéaire. Chaque octet du bloc est multiplié dans le champ de Galois par l'un des coefficients de la série (148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148, 1) selon l'ordinal numéros d'octets (une série est présentée pour les numéros de série du 15 au 0, comme indiqué sur la figure). Les octets sont ajoutés ensemble modulo 2, et les 16 octets du bloc sont décalés vers le bas, et le nombre résultant est écrit à la place de l'octet lu.

Le dernier dixième round n'est pas terminé, il ne comprend que la première opération XOR.

Grasshopper est un algorithme de bloc, il fonctionne avec des blocs de données de 128 bits ou 16 octets de long. La longueur de clé est de 256 bits (32 octets).


Figure 2. Schéma de chiffrement et de déchiffrement du bloc de données

Le diagramme montre la séquence d'opérations, où S est une transformation non linéaire, L est une transformation linéaire, Ki sont des clés rondes. La question se pose immédiatement - d'où viennent les touches rondes.

Formation de clé ronde

Les clés itératives (ou rondes) sont obtenues par certaines transformations basées sur une clé principale, dont la longueur, comme nous le savons déjà, est de 256 bits. Ce processus commence par diviser la clé principale en deux, de sorte que la première paire de clés rondes est obtenue. Huit itérations du réseau Feistel sont utilisées pour générer chaque paire suivante de clés rondes, une constante est utilisée à chaque itération, qui est calculée en appliquant une transformation linéaire de l'algorithme à la valeur du nombre d'itérations.


Le schéma d'obtention des clés itératives (rondes)

Si nous rappelons la figure 1, alors le sous-bloc gauche L est la moitié gauche de la clé d'origine, le sous-bloc droit R est la moitié droite de la clé d'origine, K est la constante Ci, la fonction f est la séquence d'opérations R XOR Ci, transformation non linéaire, transformation linéaire.

Les constantes d'itération Ci sont obtenues en utilisant la transformation L du numéro de séquence d'itération.

Ainsi, afin de crypter un bloc de texte, nous devons d'abord calculer 32 constantes itératives, puis calculer 10 clés rondes en fonction de la clé, puis effectuer la séquence d'opérations illustrée à la figure 2.

Commençons par calculer les constantes:
Premier const $$$C_1 = 1_ {10} = 00000001_2 = 01_ {16}$ , cependant, toutes les transformations de notre algorithme sont effectuées avec des blocs de 16 octets de long, il est donc nécessaire de compléter la constante avec la longueur du bloc, c'est-à-dire d'ajouter 15 octets zéro à droite, nous obtenons

$$

$$C_1 = 01000000000000000000000000000000$$

Multipliez-le par une série (1, 148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148) comme suit:

$$

$$a_ {15} = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$$

$$

$$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 +$$

$$

$$+ a_5 * 194 + a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$$

(cette égalité est donnée dans les opérations des champs de Galois)
Puisque tout sauf l'octet zéro est égal à 0 et que l'octet zéro est multiplié par 1, nous obtenons 1 et l'écrivons dans l'ordre supérieur du nombre, en décalant tous les octets dans l'ordre bas, nous obtenons:

$$

$$C_1 = 00000000000000000000000000000001$$

Répétez les mêmes opérations. Cette fois $$$a_ {15} = 1$ , tous les autres octets sont à 0, par conséquent, seul le premier reste des termes $$$a_ {15} * 148 = 1 * 148 = 148_ {10} = 94_ {16}$ nous obtenons:

$$

$$C_1 = 00000000000000000000000000000194$$

Nous faisons la troisième itération, voici deux termes non nuls:

$$

$$a_ {15} * 148 + a_ {14} * 32 = 148 * 148 + 1 * 32 =$$

$$

$$= 10010100 * 10010100 + 00000001 * 00100000 =$$

$$

$$= (x ^ 7 + x ^ 4 + x ^ 2) * (x ^ 7 + x ^ 4 + x ^ 2) + 1 * x ^ 5 = x ^ {14} + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 6 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {13} + x ^ {12} + x ^ 7 + x ^ 6 + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 5 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {11} + x ^ 5 + x ^ 7 + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 3 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {10} + x ^ 9 + x ^ 3 + x ^ 8 + x ^ 7 =$$

$$

$$= x ^ 2 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ 2 + x ^ 7 = x ^ 7 + x ^ 2 = 132_ {10}$$

$$

Selon le tableau des degrés, cela pourrait être résolu beaucoup plus facilement:

$$

$$

$$C_1 = 00000000000000000000000000019484$$

De plus, tout est exactement le même, seulement 16 itérations pour chaque constante

$$

$$C_1 = 000000000000000000000000019484DD$$

$$

$$C_1 = 0000000000000000000000019484DD10$$

$$

$$C_1 = 00000000000000000000019484DD10BD$$

$$

$$C_1 = 000000000000000000019484DD10BD27$$

$$

$$C_1 = 0000000000000000019484DD10BD275D$$

$$

$$C_1 = 00000000000000019484DD10BD275DB8$$

$$

$$C_1 = 000000000000019484DD10BD275DB87A$$

$$

$$C_1 = 0000000000019484DD10BD275DB87A48$$

$$

$$C_1 = 00000000019484DD10BD275DB87A486C$$

$$

$$C_1 = 000000019484DD10BD275DB87A486C72$$

$$

$$C_1 = 0000019484DD10BD275DB87A486C727$$

$$

$$C_1 = 00019484DD10BD275DB87A486C7276A2$$

Et la constante finale:

$$

$$C_1 = 019484DD10BD275DB87A486C7276A2E6$$

Autres constantes:

$$

$$C_2 = 02EBCB7920B94EBAB3F490D8E4EC87DC$$

$$

$$C_3 = 037F4FA4300469E70B8ED8B4969A25B2$$

$$

$$C_4 = 041555F240B19CB7A52BE3730B1BCD7B$$

$$

$$C_5 = 0581D12F500CBBEA1D51AB1F796D6F15$$

$$

$$C_6 = 06FE9E8B6008D20D16DF73ABEFF74AA7$$

$$

$$C_7 = 076A1A5670B5F550AEA53BC79D81E8C9$$

$$

$$C_8 = 082AAA2780A1FBAD895605E6163659F6$$

$$

$$C_9 = 09BE2EFA901CDCF0312C4D8A6440FB98$$

$$

$$C_ {10} = 0AC1615EA018B5173AA2953EF2DADE2A$$

$$

$$C_ {11} = 0B55E583B0A5924A82D8DD5280AC7C44$$

$$

$$C_ {12} = 0C3FFFD5C010671A2C7DE6951D2D948D$$

$$

$$C_ {13} = 0DAB7B08D0AD40479407AEF96F5B36E3$$

$$

$$C_ {14} = 0ED434ACE0A929A09F89764DF9C11351$$

$$

$$C_ {15} = 0F40B071F0140EFD27F33E218BB7B13F$$

$$

$$C_ {16} = 1054974EC3813599D1AC0A0F2C6CB22F$$

$$

$$C_ {17} = 11C01393D33C12C469D642635E1A1041$$

$$

$$C_ {18} = 12BF5C37E3387B2362589AD7C88035F3$$

$$

$$C_ {19} = 132BD8EAF3855C7EDA22D2BBBAF6979D$$

$$

$$C_ {20} = 1441C2BC8330A92E7487E97C27777F54$$

$$

$$C_ {21} = 15D54661938D8E73CCFDA1105501DD3A$$

$$

$$C_ {22} = 16AA09C5A389E794C77379A4C39BF888$$

$$

$$C_ {23} = 173E8D18B334C0C97F0931C8B1ED5AE6$$

$$

$$C_ {24} = 187E3D694320CE3458FA0FE93A5AEBD9$$

$$

$$C_ {25} = 19EAB9B4539DE969E0804785482C49B7$$

$$

$$C_ {26} = 1A95F6106399808EEB0E9F31DEB66C05$$

$$

$$C_ {27} = 1B0172CD7324A7D35374D75DACC0CE6B$$

$$

$$C_ {28} = 1C6B689B03915283FDD1EC9A314126A2$$

$$

$$C_ {29} = 1DFFEC46132C75DE45ABA4F6433784CC$$

$$

$$C_ {30} = 1E80A3E223281C394E257C42D5ADA17E$$

$$

$$C_ {31} = 1F14273F33953B64F65F342EA7DB0310$$

$$

$$C_ {32} = 20A8ED9C45C16AF1619B141E58D8A75E$$

Maintenant, nous allons calculer les clés rondes selon le schéma présenté ci-dessus, prenez la clé de cryptage:

$$

$$K = 7766554433221100FFEEDDCCBBAA9988$$

$$

$$EFCDAB89674523011032547698BADCFE$$

Alors

$$

$$K_1 = 7766554433221100FFEEDDCCBBAA9988$$

$$

$$K_2 = EFCDAB89674523011032547698BADCFE$$

$$$K_1$ sera le sous-bloc gauche du réseau Feistel, et $$$K_2$ - à droite.
Faisons l'opération $$$K_1 + C_1$
Premier octet $$$K_1$ est égal à $$
Premier octet $$$C_1$ est égal à $$$01_ {16} = 00000001_2$

$$

les octets restants sont convertis de la même manière, par conséquent $$$X (K_1, C_1) = K_1 + C_1$ :

$$

$$X (K_1, C_1) = 76F2D199239F365D479495A0C9DC3BE6$$

Ensuite, nous effectuons une transformation non linéaire $$$S (X (K_1, C_1))$ . Elle est réalisée selon le tableau:


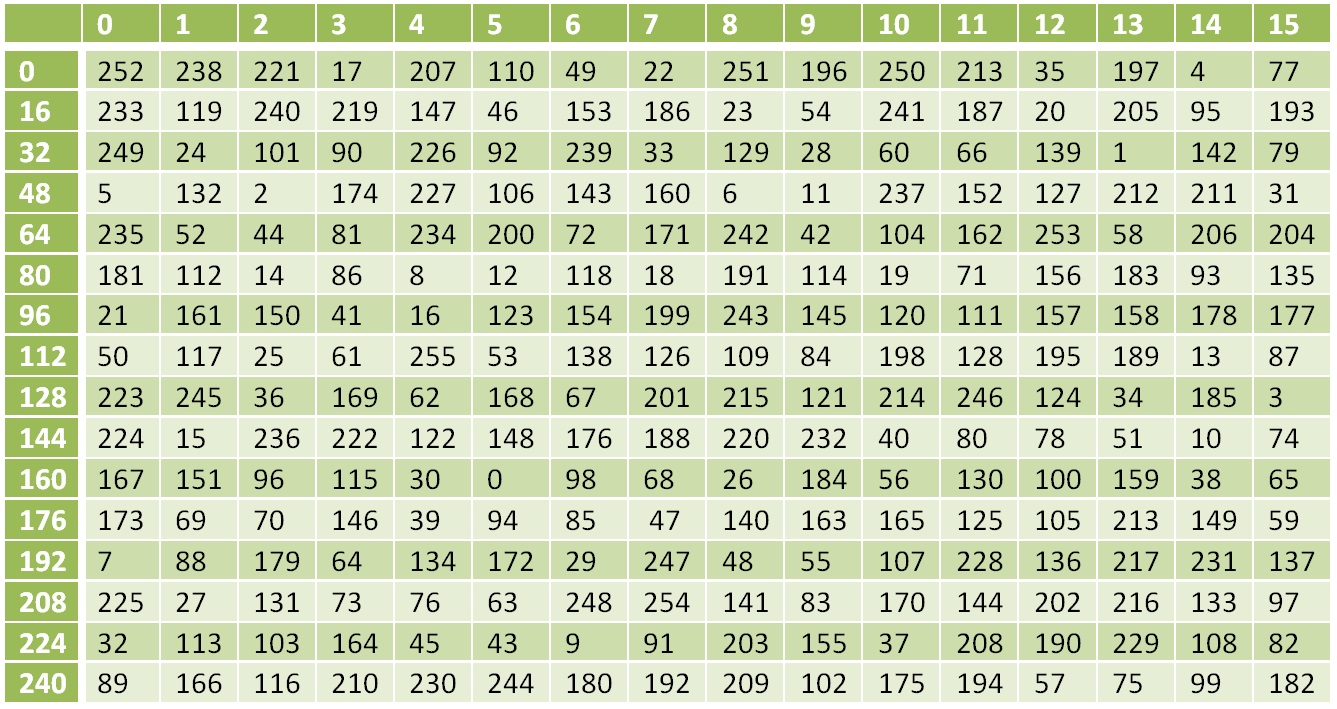Table de conversion non linéaire

Le nombre 0 est remplacé par 252, 1 par 238, 17 par 119, etc.

$$

$$

$$S (118) = 138_ {10} = 8A_ {16}$$

$$

$$S (X (K_1, C_1)) = 8A741BE85A4A8FB7AB7A94A737CA9809$$

Effectuez maintenant une transformation linéaire $$$L (S (X (K_1, C_1)))$ , il a été considéré en détail lors du calcul des constantes itératives, nous ne donnons donc ici que le résultat final:

$$

$$L (S (X (K_1, C_1))) = A644615E1D0757926A5DB79D9940093D$$

Selon le schéma de la cellule Feistel, nous effectuons XOR avec le sous-bloc droit, c'est-à-dire avec $$$K_2$ :

$$

$$X (L (S (X (K_1, C_1)))), K_2) = 4989CAD77A4274937A6FE3EB01FAD5C3$$

Et le résultat obtenu en sortie de la première cellule Feistel:

$$

$$EFCDAB89674523011032547698BADCFE4989CAD77A4274937A6FE3EB01FAD5C3$$

Cette valeur est divisée par deux et va à l'entrée de la deuxième cellule Feistel, où la deuxième constante est déjà utilisée $$$C_2$ . Après avoir parcouru huit cellules, nous obtenons les 2 clés suivantes $$$K_3$ et $$$K_4$ . Nous effectuerons avec eux huit itérations du réseau Feistel, obtiendrons la prochaine paire de clés, etc. Huit itérations par paire de clés, puisque nous avons initialement la première paire, puis 32 itérations sont effectuées au total, chacune avec sa propre constante.

Clés restantes:

$$

$$K_3 = 448CC78CEF6A8D2243436915534831DB$$

$$

$$K_4 = 04FD9F0AC4ADEB1568ECCFE9D853453D$$

$$

$$K_5 = ACF129F44692E5D3285E4AC468646457$$

$$

$$K_6 = 1B58DA3428E832B532645C16359407BD$$

$$

$$K_7 = B198005A26275770DE45877E7540E651$$

$$

$$K_8 = 84F98622A2912AD73EDD9F7B0125795A$$

$$

$$K_9 = 17E5B6CD732FF3A52331C77853E244BB$$

$$

$$K_ {10} = 43404A8EA8BA5D755BF4BC1674DDE972$$

Bloquer le chiffrement

Nous avons calculé toutes les clés et maintenant nous pouvons enfin passer directement au cryptage du bloc de texte et si vous lisez attentivement tout ce qui est écrit ci-dessus, le cryptage du texte ne sera pas difficile, car toutes les opérations utilisées dans ce processus et leur séquence ont été examinées en détail.

Prenez le bloc de texte en clair:

$$

$$T = 8899AABBCCDDEEFF0077665544332211$$

exécuter la séquence d'opérations X, S, L

$$

$$X (T, K_1) = FFFFFFFFFFFFFFFFFFF99BB99FF99BB99$$

$$

$$S (X (T, K_1)) = B6B6B6B6B6B6B6B6B6E87DE8B6E87DE8$$

$$

$$L (S (X (T, K_1))) = 30081449922F4ACFA1B055E386B697E2$$

$$

$$T_1 = 30081449922F4ACFA1B055E386B697E2$$

$$

$$X (T_1, K_2) = DFC5BFC0F56A69CEB18201951E0C4B1C$$

$$

$$S (X (T_1, K_2)) = 61AC3B07F47891E74524EE945F23A214$$

$$

$$L (S (X (T_1, K_2))) = 7290C6A158426FB396D562087A495E28$$

$$

$$T_2 = 7290C6A158426FB396D562087A495E28$$

et ainsi de suite, le résultat final ressemblera à ceci:

$$

$$T_ {10} = CDEDD4B9428D465A3024BCBE909D677F$$

Bloquer le déchiffrement

Pour déchiffrer le texte, vous devez utiliser les opérations inverses dans l'ordre inverse (voir Fig. 2).

L'opération XOR est inversée à elle-même, l'inverse de l'opération S est la substitution selon le tableau suivant:


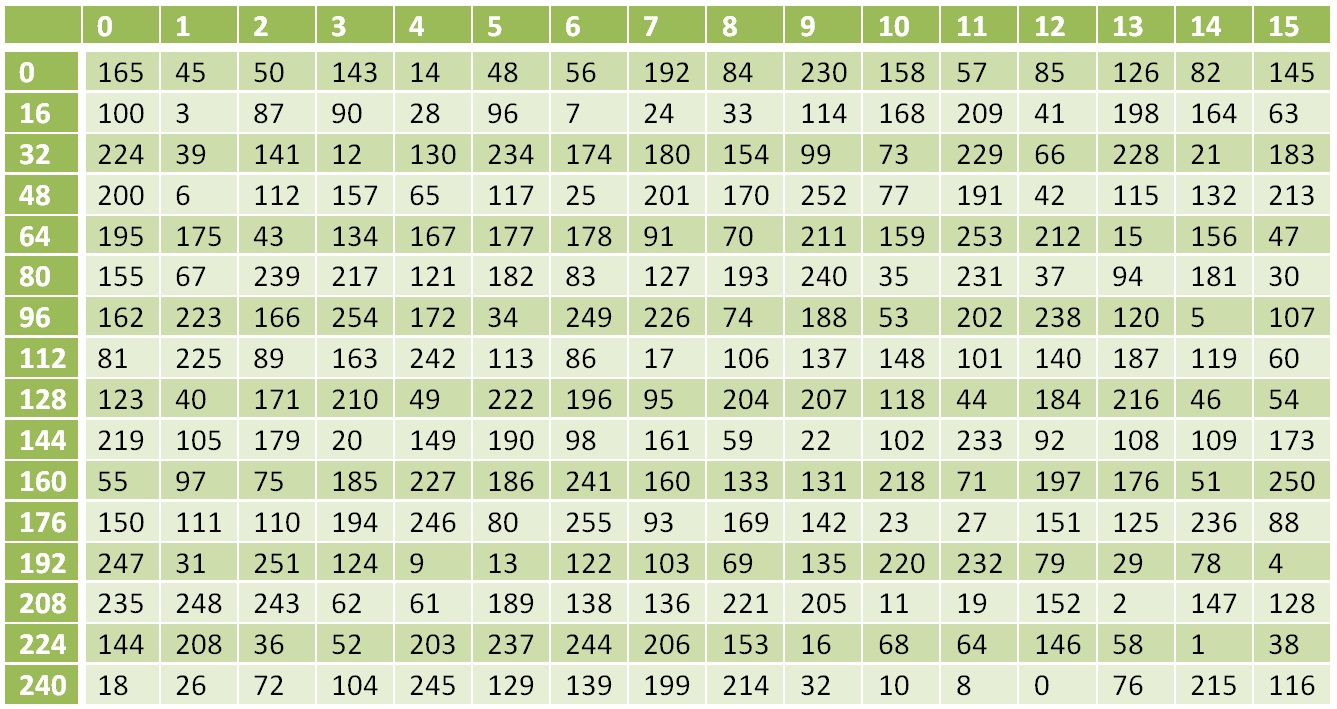Tableau de transformation non linéaire inverse

La transformation inverse en fonction L sera:

$$

$$a_0 = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$$

$$

$$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 + a_5 * 194 +$$

$$

$$+ a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$$

et un changement dans la direction du niveau supérieur. (Répéter l'opération 16 fois)

Implémentation Java

Tout d'abord, nous définissons les constantes nécessaires

static final int BLOCK_SIZE = 16; //   //     static final byte[] Pi = { (byte) 0xFC, (byte) 0xEE, (byte) 0xDD, 0x11, (byte) 0xCF, 0x6E, 0x31, 0x16, (byte) 0xFB, (byte) 0xC4, (byte) 0xFA, (byte) 0xDA, 0x23, (byte) 0xC5, 0x04, 0x4D, (byte) 0xE9, 0x77, (byte) 0xF0, (byte) 0xDB, (byte) 0x93, 0x2E, (byte) 0x99, (byte) 0xBA, 0x17, 0x36, (byte) 0xF1, (byte) 0xBB, 0x14, (byte) 0xCD, 0x5F, (byte) 0xC1, (byte) 0xF9, 0x18, 0x65, 0x5A, (byte) 0xE2, 0x5C, (byte) 0xEF, 0x21, (byte) 0x81, 0x1C, 0x3C, 0x42, (byte) 0x8B, 0x01, (byte) 0x8E, 0x4F, 0x05, (byte) 0x84, 0x02, (byte) 0xAE, (byte) 0xE3, 0x6A, (byte) 0x8F, (byte) 0xA0, 0x06, 0x0B, (byte) 0xED, (byte) 0x98, 0x7F, (byte) 0xD4, (byte) 0xD3, 0x1F, (byte) 0xEB, 0x34, 0x2C, 0x51, (byte) 0xEA, (byte) 0xC8, 0x48, (byte) 0xAB, (byte) 0xF2, 0x2A, 0x68, (byte) 0xA2, (byte) 0xFD, 0x3A, (byte) 0xCE, (byte) 0xCC, (byte) 0xB5, 0x70, 0x0E, 0x56, 0x08, 0x0C, 0x76, 0x12, (byte) 0xBF, 0x72, 0x13, 0x47, (byte) 0x9C, (byte) 0xB7, 0x5D, (byte) 0x87, 0x15, (byte) 0xA1, (byte) 0x96, 0x29, 0x10, 0x7B, (byte) 0x9A, (byte) 0xC7, (byte) 0xF3, (byte) 0x91, 0x78, 0x6F, (byte) 0x9D, (byte) 0x9E, (byte) 0xB2, (byte) 0xB1, 0x32, 0x75, 0x19, 0x3D, (byte) 0xFF, 0x35, (byte) 0x8A, 0x7E, 0x6D, 0x54, (byte) 0xC6, (byte) 0x80, (byte) 0xC3, (byte) 0xBD, 0x0D, 0x57, (byte) 0xDF, (byte) 0xF5, 0x24, (byte) 0xA9, 0x3E, (byte) 0xA8, (byte) 0x43, (byte) 0xC9, (byte) 0xD7, 0x79, (byte) 0xD6, (byte) 0xF6, 0x7C, 0x22, (byte) 0xB9, 0x03, (byte) 0xE0, 0x0F, (byte) 0xEC, (byte) 0xDE, 0x7A, (byte) 0x94, (byte) 0xB0, (byte) 0xBC, (byte) 0xDC, (byte) 0xE8, 0x28, 0x50, 0x4E, 0x33, 0x0A, 0x4A, (byte) 0xA7, (byte) 0x97, 0x60, 0x73, 0x1E, 0x00, 0x62, 0x44, 0x1A, (byte) 0xB8, 0x38, (byte) 0x82, 0x64, (byte) 0x9F, 0x26, 0x41, (byte) 0xAD, 0x45, 0x46, (byte) 0x92, 0x27, 0x5E, 0x55, 0x2F, (byte) 0x8C, (byte) 0xA3, (byte) 0xA5, 0x7D, 0x69, (byte) 0xD5, (byte) 0x95, 0x3B, 0x07, 0x58, (byte) 0xB3, 0x40, (byte) 0x86, (byte) 0xAC, 0x1D, (byte) 0xF7, 0x30, 0x37, 0x6B, (byte) 0xE4, (byte) 0x88, (byte) 0xD9, (byte) 0xE7, (byte) 0x89, (byte) 0xE1, 0x1B, (byte) 0x83, 0x49, 0x4C, 0x3F, (byte) 0xF8, (byte) 0xFE, (byte) 0x8D, 0x53, (byte) 0xAA, (byte) 0x90, (byte) 0xCA, (byte) 0xD8, (byte) 0x85, 0x61, 0x20, 0x71, 0x67, (byte) 0xA4, 0x2D, 0x2B, 0x09, 0x5B, (byte) 0xCB, (byte) 0x9B, 0x25, (byte) 0xD0, (byte) 0xBE, (byte) 0xE5, 0x6C, 0x52, 0x59, (byte) 0xA6, 0x74, (byte) 0xD2, (byte) 0xE6, (byte) 0xF4, (byte) 0xB4, (byte) 0xC0, (byte) 0xD1, 0x66, (byte) 0xAF, (byte) 0xC2, 0x39, 0x4B, 0x63, (byte) 0xB6 }; //     static final byte[] reverse_Pi = { (byte) 0xA5, 0x2D, 0x32, (byte) 0x8F, 0x0E, 0x30, 0x38, (byte) 0xC0, 0x54, (byte) 0xE6, (byte) 0x9E, 0x39, 0x55, 0x7E, 0x52, (byte) 0x91, 0x64, 0x03, 0x57, 0x5A, 0x1C, 0x60, 0x07, 0x18, 0x21, 0x72, (byte) 0xA8, (byte) 0xD1, 0x29, (byte) 0xC6, (byte) 0xA4, 0x3F, (byte) 0xE0, 0x27, (byte) 0x8D, 0x0C, (byte) 0x82, (byte) 0xEA, (byte) 0xAE, (byte) 0xB4, (byte) 0x9A, 0x63, 0x49, (byte) 0xE5, 0x42, (byte) 0xE4, 0x15, (byte) 0xB7, (byte) 0xC8, 0x06, 0x70, (byte) 0x9D, 0x41, 0x75, 0x19, (byte) 0xC9, (byte) 0xAA, (byte) 0xFC, 0x4D, (byte) 0xBF, 0x2A, 0x73, (byte) 0x84, (byte) 0xD5, (byte) 0xC3, (byte) 0xAF, 0x2B, (byte) 0x86, (byte) 0xA7, (byte) 0xB1, (byte) 0xB2, 0x5B, 0x46, (byte) 0xD3, (byte) 0x9F, (byte) 0xFD, (byte) 0xD4, 0x0F, (byte) 0x9C, 0x2F, (byte) 0x9B, 0x43, (byte) 0xEF, (byte) 0xD9, 0x79, (byte) 0xB6, 0x53, 0x7F, (byte) 0xC1, (byte) 0xF0, 0x23, (byte) 0xE7, 0x25, 0x5E, (byte) 0xB5, 0x1E, (byte) 0xA2, (byte) 0xDF, (byte) 0xA6, (byte) 0xFE, (byte) 0xAC, 0x22, (byte) 0xF9, (byte) 0xE2, 0x4A, (byte) 0xBC, 0x35, (byte) 0xCA, (byte) 0xEE, 0x78, 0x05, 0x6B, 0x51, (byte) 0xE1, 0x59, (byte) 0xA3, (byte) 0xF2, 0x71, 0x56, 0x11, 0x6A, (byte) 0x89, (byte) 0x94, 0x65, (byte) 0x8C, (byte) 0xBB, 0x77, 0x3C, 0x7B, 0x28, (byte) 0xAB, (byte) 0xD2, 0x31, (byte) 0xDE, (byte) 0xC4, 0x5F, (byte) 0xCC, (byte) 0xCF, 0x76, 0x2C, (byte) 0xB8, (byte) 0xD8, 0x2E, 0x36, (byte) 0xDB, 0x69, (byte) 0xB3, 0x14, (byte) 0x95, (byte) 0xBE, 0x62, (byte) 0xA1, 0x3B, 0x16, 0x66, (byte) 0xE9, 0x5C, 0x6C, 0x6D, (byte) 0xAD, 0x37, 0x61, 0x4B, (byte) 0xB9, (byte) 0xE3, (byte) 0xBA, (byte) 0xF1, (byte) 0xA0, (byte) 0x85, (byte) 0x83, (byte) 0xDA, 0x47, (byte) 0xC5, (byte) 0xB0, 0x33, (byte) 0xFA, (byte) 0x96, 0x6F, 0x6E, (byte) 0xC2, (byte) 0xF6, 0x50, (byte) 0xFF, 0x5D, (byte) 0xA9, (byte) 0x8E, 0x17, 0x1B, (byte) 0x97, 0x7D, (byte) 0xEC, 0x58, (byte) 0xF7, 0x1F, (byte) 0xFB, 0x7C, 0x09, 0x0D, 0x7A, 0x67, 0x45, (byte) 0x87, (byte) 0xDC, (byte) 0xE8, 0x4F, 0x1D, 0x4E, 0x04, (byte) 0xEB, (byte) 0xF8, (byte) 0xF3, 0x3E, 0x3D, (byte) 0xBD, (byte) 0x8A, (byte) 0x88, (byte) 0xDD, (byte) 0xCD, 0x0B, 0x13, (byte) 0x98, 0x02, (byte) 0x93, (byte) 0x80, (byte) 0x90, (byte) 0xD0, 0x24, 0x34, (byte) 0xCB, (byte) 0xED, (byte) 0xF4, (byte) 0xCE, (byte) 0x99, 0x10, 0x44, 0x40, (byte) 0x92, 0x3A, 0x01, 0x26, 0x12, 0x1A, 0x48, 0x68, (byte) 0xF5, (byte) 0x81, (byte) 0x8B, (byte) 0xC7, (byte) 0xD6, 0x20, 0x0A, 0x08, 0x00, 0x4C, (byte) 0xD7, 0x74 }; //    static final byte[] l_vec = { 1, (byte) 148, 32, (byte) 133, 16, (byte) 194, (byte) 192, 1, (byte) 251, 1, (byte) 192, (byte) 194, 16, (byte) 133, 32, (byte) 148 }; //     static byte[][] iter_C = new byte[32][16]; //     static byte[][] iter_key = new byte[10][64]; 

Créons toutes les fonctions principales:

 //  X static private byte[] GOST_Kuz_X(byte[] a, byte[] b) { int i; byte[] c = new byte[BLOCK_SIZE]; for (i = 0; i < BLOCK_SIZE; i++) c[i] = (byte) (a[i] ^ b[i]); return c; } //  S static private byte[] GOST_Kuz_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = Pi[data]; } return out_data; } 

Pour implémenter la fonction L, nous avons besoin de plusieurs fonctions auxiliaires, une pour calculer la multiplication des nombres dans le champ de Galois, et une pour le décalage.

 //     static private byte GOST_Kuz_GF_mul(byte a, byte b) { byte c = 0; byte hi_bit; int i; for (i = 0; i < 8; i++) { if ((b & 1) == 1) c ^= a; hi_bit = (byte) (a & 0x80); a <<= 1; if (hi_bit < 0) a ^= 0xc3; // x^8+x^7+x^6+x+1 b >>= 1; } return c; } //  R     ,    L- static private byte[] GOST_Kuz_R(byte[] state) { int i; byte a_15 = 0; byte[] internal = new byte[16]; for (i = 15; i >= 0; i--) { if(i == 0) internal[15] = state[i]; else internal[i - 1] = state[i]; a_15 ^= GOST_Kuz_GF_mul(state[i], l_vec[i]); } internal[15] = a_15; return internal; } static private byte[] GOST_Kuz_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal = in_data; for (i = 0; i < 16; i++) { internal = GOST_Kuz_R(internal); } out_data = internal; return out_data; } 

Fonctions inverses:

 //  S^(-1) static private byte[] GOST_Kuz_reverse_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = reverse_Pi[data]; } return out_data; } static private byte[] GOST_Kuz_reverse_R(byte[] state) { int i; byte a_0; a_0 = state[15]; byte[] internal = new byte[16]; for (i = 1; i < 16; i++) { internal[i] = state[i - 1]; a_0 ^= GOST_Kuz_GF_mul(internal[i], l_vec[i]); } internal[0] = a_0; return internal; } static private byte[] GOST_Kuz_reverse_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal; internal = in_data; for (i = 0; i < 16; i++) internal = GOST_Kuz_reverse_R(internal); out_data = internal; return out_data; } //    static private void GOST_Kuz_Get_C() { int i; byte[][] iter_num = new byte[32][16]; for (i = 0; i < 32; i++) { for(int j = 0; j < BLOCK_SIZE; j++) iter_num[i][j] = 0; iter_num[i][0] = (byte) (i+1); } for (i = 0; i < 32; i++) { iter_C[i] = GOST_Kuz_L(iter_num[i]); } } // ,     static private byte[][] GOST_Kuz_F(byte[] in_key_1, byte[] in_key_2, byte[] iter_const) { byte[] internal; byte[] out_key_2 = in_key_1; internal = GOST_Kuz_X(in_key_1, iter_const); internal = GOST_Kuz_S(internal); internal = GOST_Kuz_L(internal); byte[] out_key_1 = GOST_Kuz_X(internal, in_key_2); byte key[][] = new byte[2][]; key[0] = out_key_1; key[1] = out_key_2; return key; } //     public void GOST_Kuz_Expand_Key(byte[] key_1, byte[] key_2) { int i; byte[][] iter12 = new byte[2][]; byte[][] iter34 = new byte[2][]; GOST_Kuz_Get_C(); iter_key[0] = key_1; iter_key[1] = key_2; iter12[0] = key_1; iter12[1] = key_2; for (i = 0; i < 4; i++) { iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[0 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[1 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[2 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[3 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[4 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[5 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[6 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[7 + 8 * i]); iter_key[2 * i + 2] = iter12[0]; iter_key[2 * i + 3] = iter12[1]; } } //    public byte[] GOST_Kuz_Encript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; for(i = 0; i < 9; i++) { out_blk = GOST_Kuz_X(iter_key[i], out_blk); out_blk = GOST_Kuz_S(out_blk); out_blk = GOST_Kuz_L(out_blk); } out_blk = GOST_Kuz_X(out_blk, iter_key[9]); return out_blk; } //   public byte[] GOST_Kuz_Decript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; out_blk = GOST_Kuz_X(out_blk, iter_key[9]); for(i = 8; i >= 0; i--) { out_blk = GOST_Kuz_reverse_L(out_blk); out_blk = GOST_Kuz_reverse_S(out_blk); out_blk = GOST_Kuz_X(iter_key[i], out_blk); } return out_blk; } 

Eh bien, et la fonction principale

 static byte[] key_1 = {0x77, 0x66, 0x55, 0x44, 0x33, 0x22, 0x11, 0x00, (byte) 0xff, (byte) 0xee, (byte) 0xdd, (byte) 0xcc, (byte) 0xbb, (byte) 0xaa, (byte) 0x99, (byte) 0x88}; static byte[] key_2 = {(byte) 0xef, (byte) 0xcd, (byte) 0xab, (byte) 0x89, 0x67, 0x45, 0x23, 0x01, 0x10, 0x32, 0x54, 0x76, (byte) 0x98, (byte) 0xba, (byte) 0xdc, (byte) 0xfe}; static byte[] blk = DatatypeConverter.parseHexBinary("8899aabbccddeeff0077665544332211"); public static void main(String[] args) { GOST_Kuz_Expand_Key(key_1, key_2); byte[] encriptBlok = GOST_Kuz_Encript(blk); System.out.println(DatatypeConverter.printHexBinary(encriptBlok)); byte[] decriptBlok = GOST_Kuz_Decript(encriptBlok); System.out.println(DatatypeConverter.printHexBinary(decriptBlok)); } 

Nous avons appris à crypter un bloc de données afin de crypter du texte dont la longueur est plus longue que la longueur du bloc; il existe plusieurs modes décrits dans la norme - GOST 34.13-2015:

• mode de remplacement simple (Electronic Codebook, ECB);
• mode gamma (compteur, CTR);
• mode gamma avec retour de sortie (Output Feedback, OFB);
• mode d'engrenage de remplacement simple (Cipher Block Chaining, CBC);
• mode gamma avec rétroaction en texte chiffré (Cipher Feedback, CFB);
• Mode de code d'authentification de message (MAC).

Dans tous les modes, la longueur du texte doit toujours être un multiple de la longueur du bloc, de sorte que le texte est toujours complété à droite avec un seul bit et des zéros à la longueur du bloc.

Le mode le plus simple est le mode de remplacement simple. Dans ce mode, le texte est divisé en blocs, puis chaque bloc est chiffré séparément des autres, puis les blocs du texte chiffré sont collés ensemble et nous obtenons un message chiffré. Ce mode est à la fois le plus simple et le plus vulnérable et n'est pratiquement jamais appliqué en pratique.

D'autres modes pourront être examinés en détail ultérieurement.