Structure de données de l'arbre B

Bonjour à tous! Nous avons lancé un nouvel ensemble pour le cours "Algorithmes pour les développeurs" et aujourd'hui nous voulons partager une traduction intéressante préparée pour les étudiants de ce cours.



Dans les arbres de recherche, tels que l'arbre de recherche binaire, l'arbre AVL, l'arbre rouge-noir, etc. chaque nœud contient une seule valeur (clé) et un maximum de deux descendants. Cependant, il existe un type spécial d'arbre de recherche appelé B-tree (prononcé Bi-tree). Dans celui-ci, le nœud contient plus d'une valeur (clé) et plus de deux descendants. L'arbre B a été développé en 1972 par Bayer et McCrate et a été appelé l' arbre de recherche m-way à hauteur équilibrée . Son nom moderne B-tree a reçu plus tard.

Un arbre B peut être défini comme suit:
Un arbre B est un arbre de recherche équilibré dans lequel chaque nœud contient de nombreuses clés et a plus de deux enfants.

Ici, le nombre de clés dans le nœud et le nombre de ses descendants dépendent de l'ordre de l'arbre B. Chaque arbre B a une commande.

Un arbre B d'ordre m a les propriétés suivantes:

Propriété 1: La profondeur de toutes les feuilles est la même.
Propriété 2: Tous les nœuds à l'exception de la racine doivent avoir au moins (m / 2) - 1 clés et un maximum de m-1 clés.
Propriété 3: Tous les nœuds sans feuilles, à l'exception de la racine (c'est-à-dire tous les nœuds internes), doivent avoir un minimum de m / 2 descendants.
Propriété 4: si la racine est un nœud sans feuilles, elle doit avoir au moins 2 descendants.
Propriété 5: Un nœud sans feuilles avec n-1 clés doit avoir n enfants.
Propriété 6: Toutes les clés du nœud doivent être organisées dans l'ordre croissant de leurs valeurs.

Par exemple, un arbre B de 4 ordres contient un maximum de 3 valeurs clés et un maximum de 4 enfants pour chaque nœud.


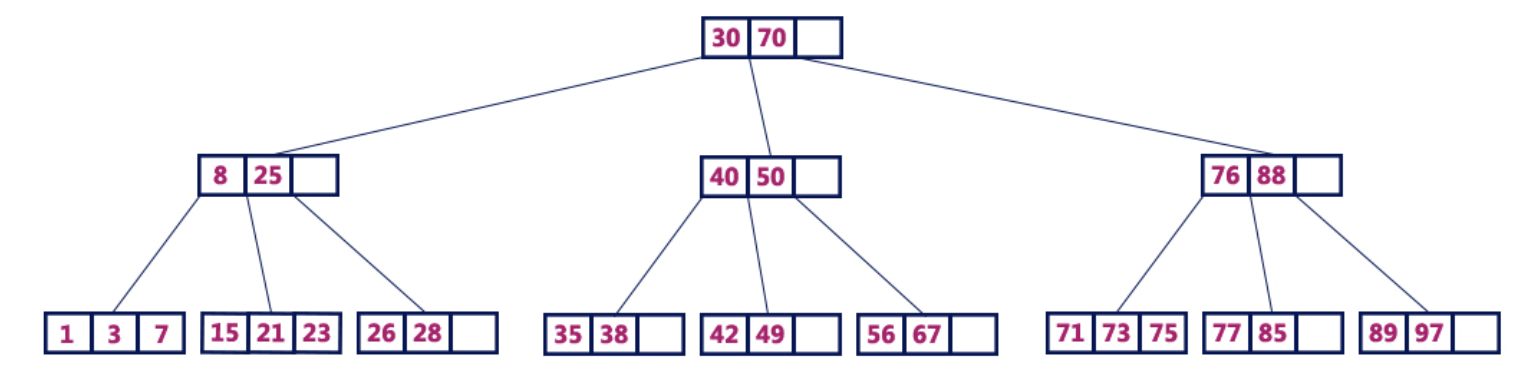B-tree 4 commandes

Opérations B-tree

Les opérations suivantes peuvent être effectuées sur l'arbre B:

1. Chercher
2. Insérer
3. Effacer

Recherche B-tree

Les recherches d'arbre B sont similaires aux recherches d'arbre binaire. Dans l'arborescence de recherche binaire, la recherche démarre à partir de la racine et chaque fois qu'une décision bidirectionnelle est prise (parcourez le sous-arbre gauche ou droit). Dans l'arbre B, la recherche commence également à partir du nœud racine, mais à chaque étape, une décision à n côtés est prise, où n est le nombre total de descendants du nœud en question. Dans l'arbre B, la complexité de recherche est O (log n) . La recherche est la suivante:

Étape 1: Lisez l'élément à rechercher.
Étape 2: Comparez l'élément recherché avec la première valeur de clé dans le nœud racine de l'arborescence.
Étape 3: S'ils correspondent, imprimez: "Le nœud a été trouvé!" et terminer la recherche.
Étape 4: S'ils ne correspondent pas, vérifiez que la valeur de l'élément est supérieure ou inférieure à la valeur de clé actuelle.
Étape 5: Si l'élément que vous recherchez est plus petit, continuez à rechercher le sous-arbre de gauche.
Étape 6: Si l'élément souhaité est plus grand, comparez l'élément avec la valeur de clé suivante dans le nœud et répétez les étapes 3, 4, 5 et 6 jusqu'à ce qu'une correspondance soit trouvée ou jusqu'à ce que l'élément recherché soit comparé à la dernière valeur de clé dans le nœud feuille.
Étape 7: si la dernière valeur de clé dans le nœud de liste ne correspond pas à la recherche, imprimez «Élément introuvable!» et terminer la recherche.

Opération d'insertion d'arbre B

Dans l'arborescence B, un nouvel élément ne peut être ajouté qu'à un nœud feuille. Cela signifie qu'une nouvelle paire clé-valeur est toujours ajoutée uniquement au nœud feuille. L'encart est le suivant:

Étape 1: Vérifiez si l'arborescence est vide.
Étape 2: si l'arborescence est vide, créez un nouveau nœud avec une nouvelle valeur de clé et prenez-le comme nœud racine.
Étape 3: Si l'arbre n'est pas vide, trouvez un nœud feuille approprié auquel une nouvelle valeur sera ajoutée en utilisant la logique de l'arbre de recherche binaire.
Étape 4: s'il existe une cellule vide dans le nœud feuille actuel, ajoutez une nouvelle valeur-clé au nœud feuille actuel, en suivant l'ordre croissant des valeurs clés à l'intérieur du nœud.
Étape 5: Si le nœud actuel est plein et n'a pas de cellules libres, divisez le nœud feuille en envoyant la valeur moyenne au nœud parent. Répétez l'étape jusqu'à ce que la valeur à envoyer soit validée sur le nœud.
Étape 6: Si la séparation se produit avec la racine de l'arbre, alors la moyenne devient la nouvelle racine de l'arbre et la hauteur de l'arbre augmente d'une unité.

Un exemple:

Créons un arbre B d'ordre 3 en y ajoutant des nombres de 1 à 10.

Insérer (1):
Puisque «1» est le premier élément de l'arbre, il est inséré dans un nouveau nœud et ce nœud devient la racine de l'arbre.



Insérer (2):
L'élément 2 est ajouté à un nœud feuille existant. Maintenant, nous n'avons qu'un seul nœud, c'est donc à la fois la racine et la feuille. Cette feuille a une cellule vide. «2» entre alors dans cette cellule vide.



Insérer (3):
L'élément 3 est ajouté à un nœud feuille existant. Maintenant, nous n'avons qu'un seul nœud, qui est à la fois la racine et la feuille. Cette feuille n'a pas de cellule vide. Par conséquent, nous séparons ce nœud en envoyant la valeur moyenne (2) au nœud parent. Cependant, le nœud actuel n'a pas de nœud parent. Par conséquent, la valeur moyenne devient le nœud racine de l'arbre.



Insérer (4):
L'élément «4» est plus grand que le nœud racine avec la valeur «2», tandis que le nœud racine n'est pas une feuille. Par conséquent, nous nous déplaçons le long du sous-arbre droit de "2". Nous arrivons au nœud feuille avec la valeur "3", qui a une cellule vide. Ainsi, nous pouvons insérer l'élément «4» dans cette cellule vide.



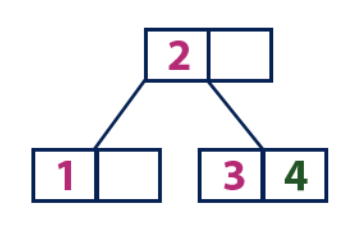Insérer (5):
L'élément «5» est plus grand que le nœud racine avec la valeur «2», tandis que le nœud racine n'est pas une feuille. Par conséquent, nous nous déplaçons le long du sous-arbre droit de "2". Nous arrivons au nœud feuille et constatons qu'il est déjà plein et qu'il n'a pas de cellules vides. Ensuite, nous divisons ce nœud en envoyant la valeur moyenne (4) au nœud parent (2). Le nœud parent a une cellule vide pour lui, donc la valeur "4" est ajoutée au nœud qui a déjà la valeur "2", et le nouvel élément "5" est ajouté en tant que nouvelle feuille.



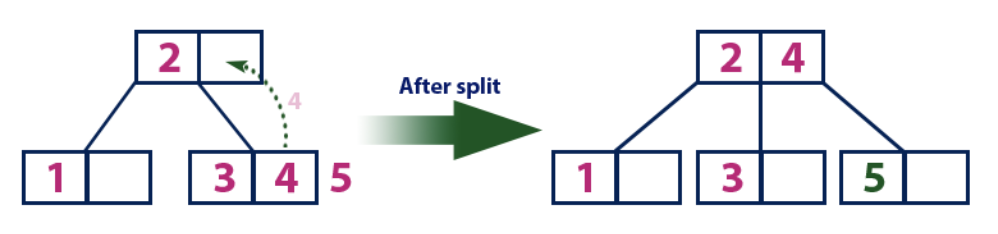Insérer (6):
L'élément "6" est plus grand que les éléments de la racine "2" et "4", qui n'est pas une feuille. Nous nous déplaçons le long du sous-arbre droit de l'élément "4". Nous atteignons une feuille avec une valeur de "5", qui a une cellule vide, donc l'élément "6" est placé juste à l'intérieur.



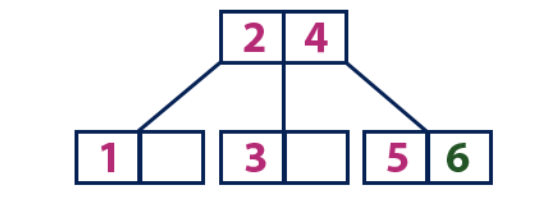Insérer (7):
L'élément "7" est plus grand que les éléments de la racine "2" et "4", qui n'est pas une feuille. Nous nous déplaçons le long du sous-arbre droit de l'élément "4". Nous atteignons le nœud foliaire et voyons qu'il est plein. Nous divisons ce nœud en envoyant la valeur moyenne de «6» au nœud parent avec les éléments «2» et «4». Cependant, le nœud parent est également plein, nous divisons donc le nœud avec les éléments «2» et «4», en envoyant la valeur «4» au nœud parent. Seul ce nœud n'est pas encore là. Dans ce cas, le nœud avec l'élément «4» devient la nouvelle racine de l'arbre.



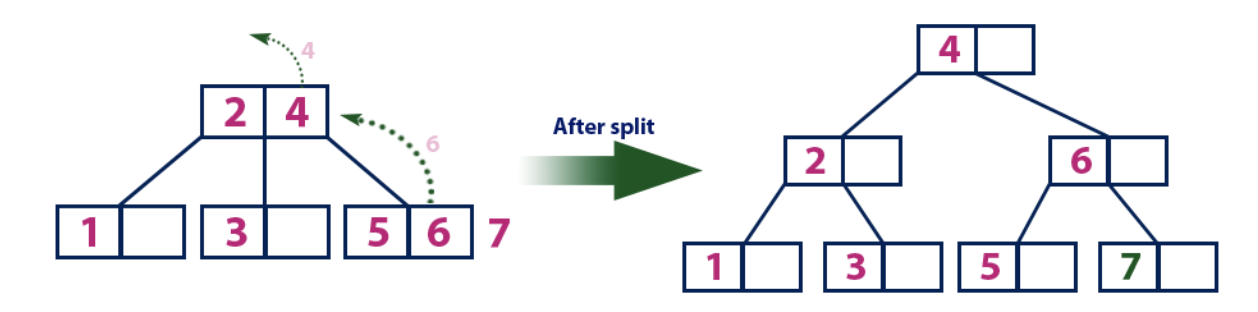Insérer (8):
L'élément 8 est plus grand que le nœud racine avec une valeur de 4, et le nœud racine n'est pas une feuille. Nous nous déplaçons le long du sous-arbre droit de l'élément "4" et arrivons au nœud avec la valeur "6". «8» est supérieur à «6» et le nœud avec l'élément «6» n'est pas une feuille, nous nous déplaçons donc le long du sous-arbre droit de «6». Nous atteignons le nœud de feuille avec "7", qui a une cellule vide, alors nous y mettons "8".



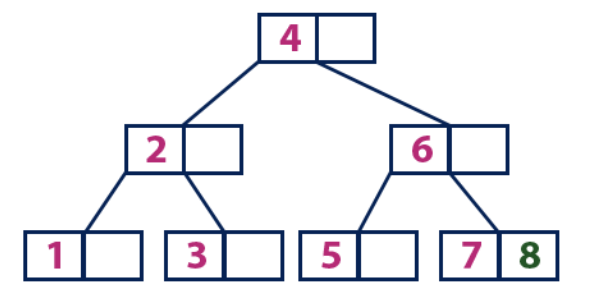Insérer (9):
L'élément 9 est plus grand que le nœud racine avec une valeur de 4, et le nœud racine n'est pas une feuille. Nous nous déplaçons le long du sous-arbre droit de l'élément "4" et arrivons au nœud avec la valeur "6". «9» est supérieur à «6» et le nœud avec l'élément «6» n'est pas une feuille, nous nous déplaçons donc le long du sous-arbre droit de «6». Nous atteignons le nœud feuille avec les valeurs "7" et "8". Il est plein. Nous divisons ce nœud en envoyant la valeur moyenne (8) au nœud parent. Le nœud parent «6» a une cellule vide, nous y mettons donc «8». Dans ce cas, un nouvel élément "9" est ajouté à la liste des nœuds.



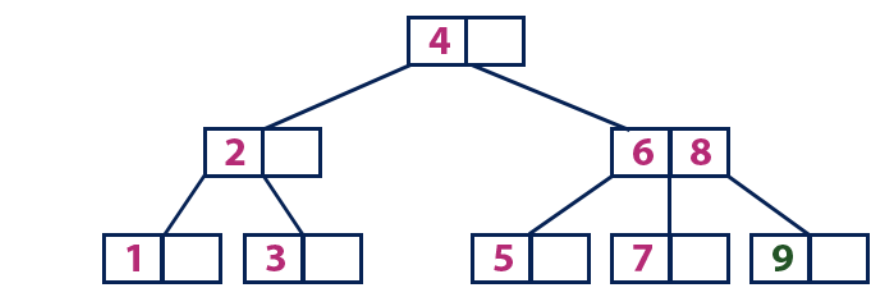
Insérer (10):
L'élément "10" est plus grand que le nœud racine avec la valeur "4", tandis que le nœud racine n'est pas une feuille. Nous nous déplaçons le long du sous-arbre droit de l'élément "4" et arrivons au nœud avec les valeurs "6" et "8". "10" est supérieur à "6" et "8" et le nœud avec ces éléments n'est pas une feuille, nous nous déplaçons donc le long du sous-arbre droit de "8". Nous atteignons le nœud feuille avec une valeur de "9". Il a une cellule vide, alors nous y avons mis "10".



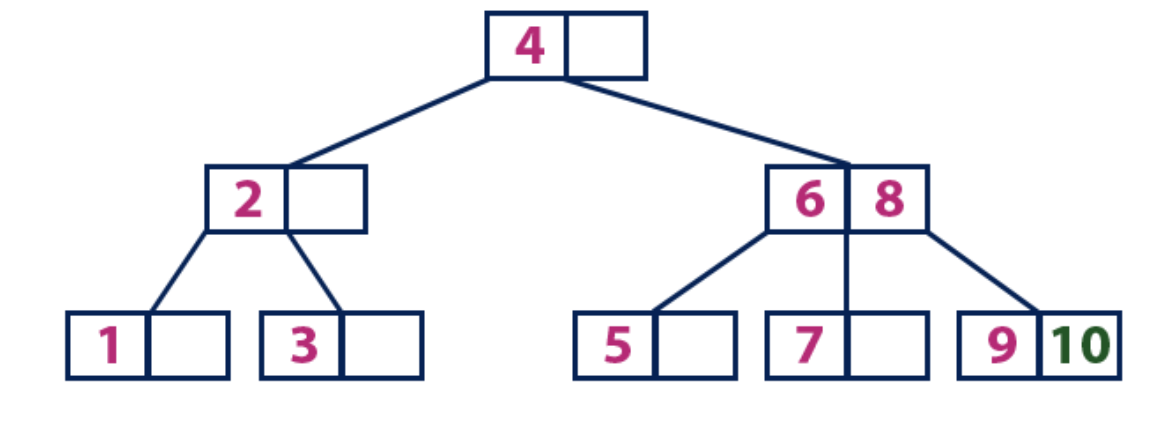
Nous vous suggérons de comprendre de manière indépendante dans la pratique comment les arbres B sont organisés à l'aide de cette visualisation .

Nous attendons tout le monde lors d'une leçon ouverte gratuite qui se tiendra le 12 juillet. A très bientôt!