Les éléments des pages Web sont principalement situés côte à côte ou les uns sous les autres. Mais parfois, la conception nécessite des éléments qui se chevauchent. Par exemple, un menu de navigation déroulant, des panneaux d'aperçu en survol, des bannières de cookies inutiles et, bien sûr, d'innombrables fenêtres contextuelles nécessitant votre attention immédiate.

Dans ces situations, le navigateur doit en quelque sorte décider quels éléments afficher "d'en haut" et quels éléments conserver en arrière-plan, complètement ou partiellement fermés. Un ensemble relativement complexe de règles dans la norme CSS définit l' ordre de fusion par défaut pour chaque élément de page (probablement tout dans le monde peut être appelé «relativement complexe», mais il est immédiatement inquiétant que la norme soit livrée avec une application spéciale intitulée «Description détaillée des contextes de fusion» ).

Si l'ordre par défaut ne convient pas, les développeurs ont recours à la propriété z-index : elle donne le contrôle sur l'axe z virtuel (profondeur), qui traverse conceptuellement la page. Ainsi, un élément avec un z-index supérieur z-index affiché «plus près» de l'utilisateur, c'est-à-dire qu'il est dessiné au-dessus des éléments avec des indices inférieurs.

Une propriété intéressante de l'axe z est qu'il n'a pas de frontières naturelles. Les axes horizontal et vertical sont généralement limités par la taille attendue de l'affichage. Nous ne nous attendons pas à ce que des éléments soient poussés à «1 000 000 pixels à gauche» ou «-3 000em en haut»: ils deviendront soit invisibles, soit provoqueront un défilement désagréable. (À moins que vous ne lisiez cet article à une époque où les écrans font des millions de pixels de large. Si c'est le cas, je vous invite à arrêter de lire et à démarrer un projet de page Web de plusieurs milliards de dollars).

Mais les valeurs de l' z-index sont sans dimension et n'ont d'importance qu'en termes relatifs: une page avec deux éléments sera identique si les indices z sont 1 et 2 ou −10 et 999 . Combiné avec le fait que les pages sont souvent assemblées à partir de composants conçus isolément, cela conduit à l'art curieux de sélectionner les z-index appropriés.

Comment vous assurer que votre pop-up ennuyeux apparaît exactement au-dessus de tous les éléments de la page si vous ne savez pas combien il y en a, qui les a écrits et combien ils voulaient être au sommet? C'est alors que vous mettez votre z-index à 100, ou peut-être 999, ou peut-être juste au cas où, à 99999 pour vous assurer que le vôtre gagnera définitivement.

C'est du moins ainsi que j'écris mon CSS. Dans le reste de cet article, nous examinerons des millions d'indices z et verrons ce que font les autres développeurs Web.

Récupération de données

La première étape a été de collecter un grand ensemble de valeurs d'index z à partir des pages Web existantes. Pour ce faire, je me suis tourné vers Common Crawl , un référentiel public, très grand et merveilleux de pages Internet. Les données sont hébergées sur S3, vous pouvez donc les demander assez efficacement à partir d'un cluster AWS. Heureusement, il existe plusieurs didacticiels sur Internet qui montrent comment procéder.

Mon extracteur d'index z sophistiqué implique de rechercher sur chaque page toutes les correspondances de l'expression régulière suivante:

 re.compile(b'z-index *: *(-?[0-9]+|auto|inherit|initial|unset)') 

Une fois les valeurs déterminées, la tâche de réduction de carte standard reste pour le nombre d'occurrences. Heureusement, je ne suis pas le premier à vouloir compter les occurrences de toutes sortes de choses dans l'échantillon, et cela a suffi pour adapter l' un des nombreux exemples . (Presque tout mon code personnel est une expression régulière en haut).

Grâce à un article de blog très détaillé, j'ai pu déployer le code sur le cluster Elastic Map Reduce , et j'ai commencé à scanner l' archive de page pour mars 2019 . Cette archive particulière est divisée en 56 000 parties, dont j'ai sélectionné au hasard 2 500, soit environ 4,4%. Ce nombre n'a rien de spécial, sauf qu'il se traduit en gros par le prix que j'étais prêt à investir dans cette expérience. Après une nuit terrible dans l'espoir de ne pas avoir fait les prévisions correctement, j'ai obtenu des résultats extraits de 112,7 millions de pages. (Je dois souligner que ce sont toutes des pages HTML. Je ne me suis pas trop penché sur cette question, mais Common Crawl ne semble pas indexer les feuilles de style externes, et par conséquent, j'extraye uniquement les valeurs de CSS en ligne. Je vais le laisser comme un exercice pour le lecteur de déterminer si la distribution résultante correspond à ce que vous obtenez des feuilles de style externes).

Les valeurs les plus courantes

Mon analyse a donné un total d'environ 176,5 millions de valeurs d'index z, dont 36,2 mille sont uniques.

Quels sont donc les plus courants?

La figure montre les 50 premiers. Notez que l'axe y est logarithmique et montre les fréquences relatives. Par exemple, la valeur la plus courante de 1 correspond à 14,6% de toutes les occurrences trouvées dans l'échantillon. En général, le top 50 représente environ 80% des valeurs collectées.



La première observation est que les valeurs positives dominent. Le seul élément négatif dans le top 50 est −1 (le deuxième −2 le plus courant prend la 70e place). Cela nous dit peut-être que les gens sont généralement plus intéressés à prendre les choses à l'étage qu'à les cacher en arrière-plan.

En règle générale, la plupart des valeurs supérieures ont l'une des propriétés suivantes:

• Ils sont petits: par exemple, tous les nombres de 0 à 12 sont dans le top 50.
  
• Ce sont des degrés de dix ou des nombres multiples: 10, 100, 1000, 2000, ...
  
• Ils sont «proches» de la puissance de dix: 1001, 999, 10001, ...

Ces modèles sont cohérents avec le fait que les gens choisissent de grandes valeurs "familières" (degrés de dix), puis, peut-être, pour ajuster la profondeur relative à l'intérieur du composant - les valeurs sont légèrement supérieures ou inférieures.

Il est également intéressant de regarder les valeurs les plus courantes qui ne correspondent à aucun de ces modèles:

À la 36ème place, nous voyons 2147483647. De nombreux programmeurs reconnaissent immédiatement ce nombre comme INT_MAX , soit 2 ³¹ -1. Les gens argumentent probablement comme ceci: puisque c'est la plus grande valeur pour un entier (signé), aucun z-index ne sera plus élevé, donc mon élément avec l'index INT_MAX sera toujours au sommet. Cependant, MDN dit ce qui suit sur les entiers en CSS:

Il n'y a pas de plage officielle de valeurs de type <integer> . Opera 12.1 prend en charge des valeurs allant jusqu'à 2 ¹⁵ -1, IE - jusqu'à 2 ²⁰ -1, et d'autres navigateurs sont encore plus élevés. Tout au long de l'existence des valeurs CSS3, plusieurs discussions ont eu lieu sur l'établissement d'une fourchette minimum supportée: la dernière décision a été prise en avril 2012 lors de la phase LC, puis la fourchette a été adoptée [-2 ²⁷ -1; 2 ²⁷ -1], mais d'autres valeurs ont été suggérées, telles que 2 ²⁴ -1 et 2 ³⁰ -1. Cependant, la dernière spécification pour le moment n'indique plus la portée de ce type de données.

Ainsi, non seulement il n'y a pas de valeur maximale convenue, mais INT_MAX fait hors de portée dans chaque spécification ou clause standard documentée.

À la 39e place, nous avons 8675309, dans lequel je n'ai personnellement rien vu de remarquable. Mais pour plus d'un demi-million de développeurs, cela a évidemment du sens. Je soupçonne que vous reconnaissez instantanément ce nombre ou que vous ne comprenez pas du tout sa signification, selon l'endroit et le moment où vous avez grandi. Je ne donnerai pas de spoilers, la réponse est cachée derrière une seule recherche .

Les deux derniers chiffres qui semblaient un peu inappropriés sont 1030 et 1050, respectivement aux 42e et 45e places. Un autre coup d'œil rapide a révélé que ce sont les valeurs par défaut de l'index z pour les navbar-fixed et modal dans Bootstrap.

Distribution des valeurs

Bien que la grande majorité de toutes les valeurs d' z-index proviennent d'un petit nombre d'options, il peut être intéressant d'examiner la distribution plus large de l'ensemble compilé. Par exemple, la figure 2 montre la fréquence de toutes les valeurs comprises entre -120 et 260.



En plus de la dominance des nombres ronds, nous constatons une qualité presque fractale des motifs à plusieurs niveaux. Par exemple, le milieu entre deux maxima locaux est souvent lui-même un maximum local (plus petit): il est de 5 entre 1 et 10, 15 entre 10 et 20, 50 entre 1 et 100, etc.

Nous pouvons confirmer cet effet sur une plage plus large: la figure suivante montre les fréquences de toutes les valeurs de -1200 à 2600, avec un arrondi à un module plus petit jusqu'à dix, c'est-à-dire que des nombres comme 356 et 359 ont été comptés comme 350. Le graphique est très similaire au précédent. Comme vous pouvez le voir, la structure est principalement préservée lorsque l'on considère des valeurs d'un ordre de grandeur plus grand.



Enfin, dans la dernière illustration, toutes les valeurs d' z-index positives de 1 à 9999999999 sont regroupées par le premier chiffre (axe horizontal) et le nombre de chiffres (axe vertical).


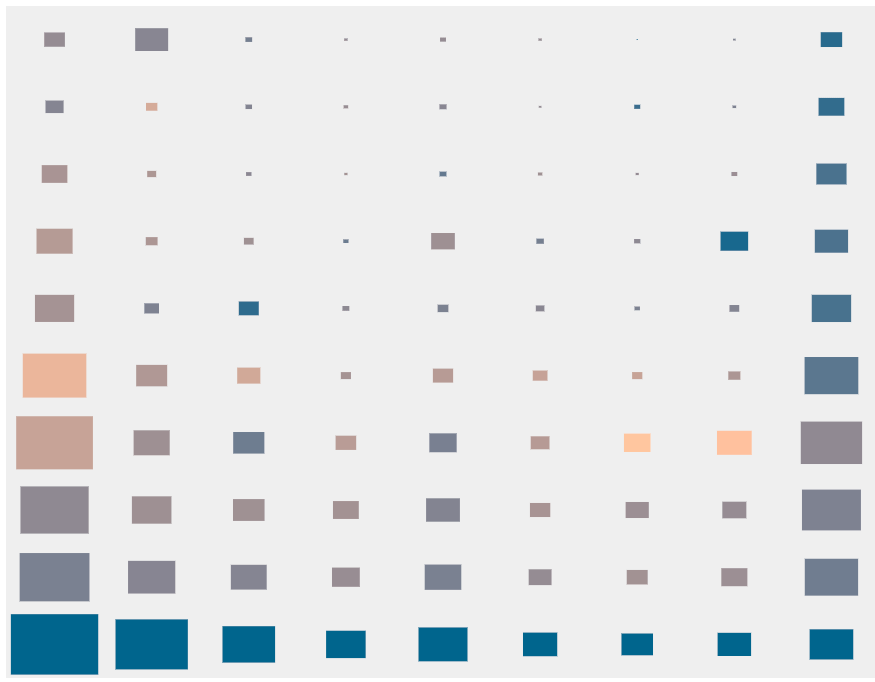Valeurs d' z-index positives regroupées par premier chiffre et nombre de chiffres. Les dimensions sont proportionnelles à la fréquence globale du groupe. Cliquez sur un groupe pour plus d'informations.

Nous pouvons intuitivement présenter chaque groupe comme un modèle de valeurs, par exemple, 3xxx pour toutes les valeurs à quatre chiffres commençant par 3. Chaque groupe est affiché sous forme de rectangle, dont la taille est proportionnelle à la fréquence du motif. La figure montre, par exemple, que pour chaque ordre de grandeur, c'est-à-dire un certain nombre de groupes, les fréquences suivent une tendance similaire, et les valeurs à partir de 1 sont les plus courantes, puis 9, puis 5.

La teinte de chaque groupe est établie en fonction de son entropie. Les groupes jaunes ont l'entropie la plus élevée, tandis que les groupes bleus ont la plus faible. Cela aide à mettre en évidence les modèles où les développeurs ont tendance à choisir les mêmes valeurs, ou ceux où les valeurs sont distribuées de manière plus uniforme (notez que l'entropie de l'ensemble de nos données est de 6,51 bits).

Conclusion

Bien qu'il ait été vraiment intéressant de collecter et de rechercher cet ensemble de données, je suis sûr qu'il existe de meilleures statistiques, visualisations et explications en attente de production et de présentation. Si vous voulez essayer, n'hésitez pas à télécharger et à distribuer le fichier z-index-data.csv .

Peut-être que vous réussirez là où j'ai échoué et que vous trouverez un moyen d'inclure dans le graphique la valeur d' z-index la plus élevée que j'ai trouvée, à savoir 10 ¹²⁴² -1.

Oui, le nombre 9 est répété 1242 fois. J'espère vraiment qu'ils ont enfin pu montrer leur <div> en haut.