Un modèle d'une série naturelle de nombres et de ses éléments. Losanges

   

Dans ce travail, le modèle de base G ^{2 ±} est conservé, mais une organisation différente de ses cellules est acceptée (autre figure). Au sommet du réseau primaire avec des cellules 1 × 1 , une grille plus grande est représentée - une grille de losanges, ainsi qu'une grille de centres de losanges est considérée (SCR). La dernière grille n'est pas représentée afin de ne pas surcharger les lignes avec le motif avec des losanges. Nous ne répéterons pas les définitions et les concepts qui ont été décrits en détail dans les travaux précédents , mais donnerons des liens pointant vers ces travaux.

Description du modèle constructif

À travers les cellules G ^{2 ±} - modèles contenus dans les diagonales Di et Ki même longues avec des nombres se terminant par des zéros dans le sous-modèle G ^{2 -} -, des lignes sont tracées qui forment un grand réseau de losanges dans le plan. Les régions rhombiques pour les cellules couvrent collectivement tout le plan sans lacunes. Chaque losange contient 41 cellules, dont seulement 16 présentent un intérêt, et lors du sondage d'un losange, seules 4 cellules à flexion fixe sont utilisées.

Les caractéristiques des losanges comprendront:

• le nombre de cellules dans le losange;
• la valeur du nombre dans la cellule centrale;
• les numéros de ses horizontaux ( N _i ) et verticaux ( V _i );
• identifier les cellules pour les nombres avec des inflexions 1, 3, 7, 9;
• les coordonnées de ces cellules dans le système de coordonnées du losange avec l'origine dans la cellule centrale du losange.

Une grille de centres de losanges est également construite à travers les cellules des centres de losanges, dont les nœuds sont situés dans les cellules à l'intersection de diagonales longues et courtes avec des nombres qui sont des multiples du nombre 5.
Sur la figure avec des losanges, il est clair quel type de grille est impliqué. Pour illustrer les caractéristiques des losanges, des images d'une paire de losanges dans chaque demi-plan sont données. Ces losanges sont marqués d'un nombre identifiant de cellules dans la moitié inférieure et d'une autre paire de tels losanges dans les demi-plans supérieurs. Le marquage des losanges dans le demi-plan en dessous de la diagonale D ₀ diffère du marquage des losanges dans le demi-plan au-dessus, mais dans le même demi-plan, le marquage de tous les losanges est identique pour les demi-plans inférieur et supérieur. L'essence du marquage est la localisation des cellules avec des nombres qui ont des inflexions égales (marquées en remplissant les cellules de la même couleur), en définissant leurs coordonnées x ₁ , x ₀ . Les losanges désignés seront appelés fondamentaux; d'autres losanges avec zoom avant peuvent en être formés.

Les centres des losanges du demi-plan inférieur sont des cellules avec des nombres se terminant par deux chiffres soit 25 avec le nombre horizontal avec flexion 5 et avec le nombre vertical avec flexion 0, ou 75 avec le nombre horizontal avec flexion 0 et avec le nombre vertical avec flexion 5. Dans le demi-plan supérieur ^{2 +} - sous-modèles, tous les nombres dans les cellules centrales de tous les losanges se terminent par deux chiffres 25. De plus, nous limitons notre examen au demi-plan ^{2 -} .


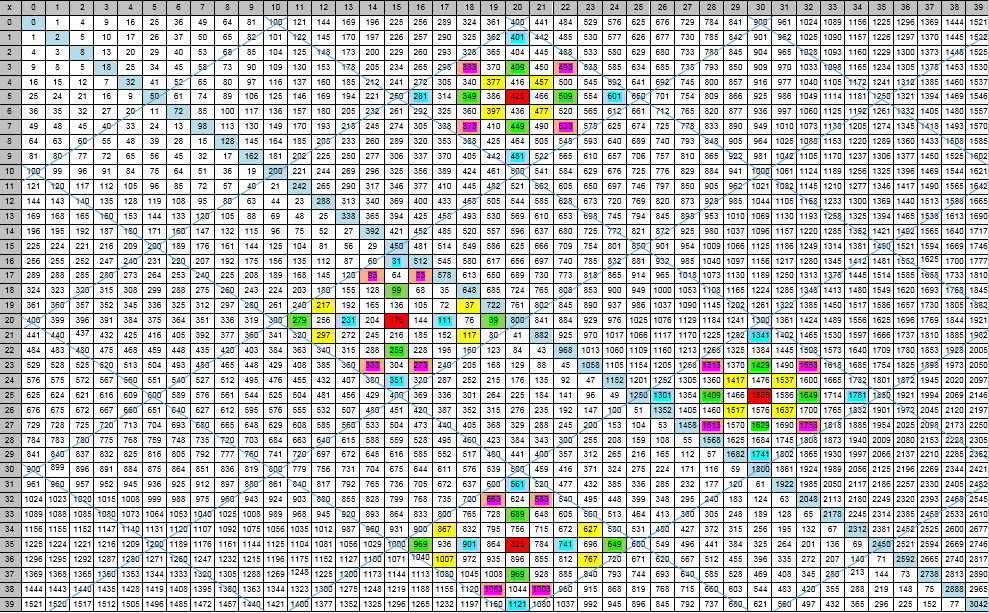_{Figure 1— Représentation visuelle d'un modèle en diamant}

Définition 1. Le losange fondamental est la structure du modèle à ^{2 ±} -, limitée par deux diagonales courtes et deux longues de ce plan avec des nombres qui sont des multiples du nombre 10. L'élément principal qui caractérise le losange est la cellule ( x _1c , x _0c ) de son centre. Le centre contient une valeur numérique de N, un multiple de 5.

Définition 2. L'ensemble des centres des losanges fondamentaux est les nœuds (cellules) du réseau des centres des losanges (SCR) des diagonales courtes et longues entrecroisées avec des nombres multiples de 5. Les losanges eux-mêmes recouvrent complètement les modèles plans ^{2 ×} - (principe du parquet).

Tous les losanges sont disposés de la même manière, et les nombres dans leurs cellules avec des terminaisons fixes sont placés dans des positions fixes (cellules). Cela vous permet de factoriser facilement ce nombre lors de la résolution du problème de localisation du nombre N dans un certain losange. Dix horizontales dont les cellules forment un losange et les losanges voisins (avec des coordonnées différentes de celui-ci) seront appelées une bande de losanges. Les bandes horizontales sont considérées: Ouest-Est (); vertical: Nord-Sud (NW), le long de courtes diagonales: Northeast (NE) et le long de longues diagonales: North-West (NW). Le décalage d'un losange à l'autre peut être complété par une indication (de haut en bas) le long des bandes indiquées, en plus d'indiquer la bande.

Puisqu'il résulte de la définition 2 que l'ensemble des cellules de tous les losanges est toutes les cellules du modèle G ^{2 ±} , puis dans l'une des cellules (x _1p , x _0p ) appartenant à un certain losange, un nombre naturel impair composite (ELF) N prédéterminé ( x _1p , x _0p ) = N (x ₁ , x ₀ ) . En même temps, nous pensons qu'il est possible d'indiquer un tel losange (en déterminant les coordonnées de sa cellule centrale) (x _1c , x _0c ) que de sonder toutes les cellules, se limitant même à sonder uniquement les diagonales impaires.

L'indication d'un tel losange et de la cellule souhaitée en son sein est une solution au problème de localisation pour un nombre N donné (x ₁ , x ₀ ) . Ce problème et sa solution précèdent la réception de la décision de la WFCH. La signification et le but ultime du problème de localisation est d'indiquer dans un certain losange pour un ELF N donné (x ₁ , x ₀ ) les valeurs des coordonnées de la cellule (x _1p , x _0p ) dans le modèle G ^{2 ±} , dans lequel il y a un nombre coïncidant avec N (x ₁ , x ₀ ) .

Dans cet article, nous utilisons le mécanisme pour établir l'appartenance d'un nombre N donné à un losange spécifique et à une cellule qu'il contient. Ce mécanisme est loin d'être le meilleur, mais dans les exemples proposés, il fait face à la tâche. Les lecteurs sont invités à proposer leur original ou à améliorer ce mécanisme.

Notre mécanisme est basé sur la régularité remarquable du modèle G ^{2 ±} découvert par l'auteur: la présence dans les lignes horizontales avec des nombres multiples de cinq (et quelques autres), des cellules avec des carrés des éléments des triplets de Pythagore (PFT) < g, k ₁ , k ₂ > = <hypoténuse , jambe ₁ , jambe ₂ >. Le CFT sera discuté dans un autre ouvrage.

Pour simplifier les conclusions et les calculs, nous aurons besoin de trois systèmes de coordonnées: planaire, qui a déjà été introduit , réseau avec d'autres nombres de diagonales pour le SCR (Fig.2) et rhombique (Tableau 1), dans lequel le début est associé à la cellule du centre du losange.


<sub>Figure 2. Numérotation (double) des diagonales courtes et
répartition des centres diamantés sur les diagonales courtes

Tableau 1. Détermination des coordonnées d'un point de recherche dans un losange fixe</sub>



Dans le système SCR, les éléments suivants sont indiqués: le numéro de la diagonale courte n _p , c est le numéro de série du centre, ainsi que le numéro du centre C à l' échelle du réseau, leur propre numérotation des diagonales courtes à partir de n _p = 1 (dans le système planaire est la 5e diagonale courte) , puis le nombre n _p = 2 (c'est le nombre augmenté de 10, soit le 15ème plan K _i ) puis à l'étape 10 tous les autres. La position de toutes les cellules des centres losanges dans chaque K _{i du} SCR est également numérotée de c = 1 à c = 2n _{p du} numéro de réseau double de la courte diagonale.

Exemple 1 Soit qu'il soit nécessaire de trouver le numéro C du réseau de l'ensemble du centre d'un des losanges et le nombre N dans cette cellule pour une courte diagonale donnée passant par les centres des losanges, son numéro de réseau n _p = 5 et le numéro de série du centre c = 3 de l' un des losanges sur celui-ci. Tout simplement, les coordonnées du réseau de la cellule centrale de ce losange sont représentées sous la forme (n _p , q) = (5, 3) .

1. Trouvez la coordonnée plane x ₁ de la cellule au début de la diagonale donnée (nd):
   x ₁ = x _nd = 10n _p - 5 = 50 - 5 = 45.
   Pour notre cas, nous avons obtenu x ₁ = x _nd = 45 .
   
2. Maintenant, nous pouvons immédiatement procéder à la recherche des coordonnées planes de la cellule ( x _1c , x _sc ) du centre souhaité: x ₁ = x _nd - 5 (c - 1) = 45 - 5 (3 - 1) = 35, x ₀ = 0 + 5 ( μ - 1) = 2 ∙ 5 = 10.
   
3. Trouvez le numéro de réseau du centre du losange ( C ).
   
   Remarque. On sait que pour le nombre x, la formule 2C _{x + 1} ² = x (x + 1) est le nombre doublé de combinaisons de x + 1 sur deux.
   Le nombre de centres précédant la courte diagonale n _p = 5 est 2n _p (n _p - 1) . Ensuite, le numéro de série C du centre de réseau est donné par la formule
   C = n _p (n _p -1) + c = 2C _{n p} ² + 3 = 5 ∙ 4 + 3 = 23 .
   
4. Trouvez la valeur du nombre N (x _1c , x _sc ) dans la cellule du centre du losange N = x ₁ ² - x ₀ ² - le signe dans la formule est pris en fonction de la position du centre par rapport à la diagonale principale.
   N = 35 ² - 10 ² = 1125 - pour notre cas.
   

Ainsi, n'ayant que le numéro de réseau n _{p de la} courte diagonale passant par les cellules des centres et le numéro de centre actuel du losange c sur cette diagonale, nous pouvons obtenir toutes les autres informations sur le centre du losange.

Tous les entiers positifs impairs d'intérêt N appartiennent aux cellules de diamant. Le concept de flexion, dernier chiffre d'un nombre, permet de localiser leur position au sein des losanges. Pour la factorisation, les nombres N qui se terminent par les nombres 1, 3, 7, 9 sont intéressants.

Les nombres pairs ne sont pas considérés comme N , car ils ont un diviseur premier 2. Les nombres se terminant par cinq ont un diviseur premier 5, ce qui est également inacceptable pour N. Il est conseillé de localiser un N spécifique par flexion dans le losange par rapport au centre du losange, dans le contexte du fait que le centre est la caractéristique la plus importante du losange. Sur la base du fait que tous les losanges ont la même structure, il existe une relation explicite entre le nombre N spécifié pour la factorisation et les nombres dans les cellules du losange avec certaines inflexions et dans la cellule du centre du losange. Les données sur ces numéros de relation sont données dans le tableau. 1.

Cependant, trier tous les losanges sur un plan pour trouver le losange souhaité est inacceptable soit en temps, soit en coût de calcul. Ainsi, le problème s'est posé de localiser les régions ^{2 -} - sous-modèles (demi-plans), y compris les losanges qui contiendraient le nombre initial N , à factoriser.

Triplets pythagoriciens . Pour résoudre le problème formulé sont utilisés
Les triplets de Pythagore sont des triplets de nombres satisfaisant le théorème de Pythagore: à savoir, les triplets de Pythagore qui satisfont à la règle du soi-disant triangle égyptien, c'est-à-dire un triangle dont les côtés sont des multiples de 3, 4, 5.
Dans chaque x ₁ horizontal contenant les centres des losanges, il y a un ou plusieurs de ces triplets pythagoriciens.

Le premier losange dans le problème de localisation est indiqué approximativement et en cas de "manque", les losanges suivants doivent être sélectionnés. Pour cela, il est nécessaire de déterminer la direction du mouvement le long du SCR, afin de se rapprocher progressivement du but final. Par exemple, si le plus petit des 4 dans le losange actuel est inférieur au N donné, alors les losanges nord-est et est de celui-ci contiennent encore moins de 4 nombres, c'est-à-dire que ces losanges ne doivent pas être sondés. Le passage au losange occidental entraîne une telle augmentation des valeurs dans les 4 cellules que même un plus petit nombre du losange occidental s'avère être plus grand que le plus grand nombre du losange précédent et, par conséquent, plus que N.D'où la solution: passer du losange au losange dans la direction nord-ouest.

Si un losange contenant une cellule avec un nombre égal à N (x _1p , x _0p ) = N est trouvé et que les coordonnées de la cellule (x _1p , x _0p ) sont déterminées, alors la solution du FBCH est déterminée par la relation de base ^{2 ±} - du modèle
N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p ∙ q

Un autre sous-problème est la sélection et la mise en œuvre de la séquence de contournement cellulaire du losange sélectionné pour le sondage. Ici, l'ordre de déplacement dans le sens inverse des aiguilles d'une montre est adopté, à partir de la cellule supérieure gauche contenant le nombre avec l'inflexion requise. Dans une situation de coïncidence des valeurs de la cellule diamant N (x _1p , x _0p ) et d'un nombre donné N (x ₁ , x ₀ ), la différence entre elles se révèle nulle.

Algorithme de solution ZFBCH utilisant des losanges fondamentaux et PFT

1. On extrait la racine du nombre N. Arrondissez.
   
2. Nous vérifions si √N est divisible par 3. Si divisible, affectez cette valeur à la première étape k1, sinon, pour remplir la propriété de divisibilité par 3, soustrayez 1 ou 2 du résultat et entrez-la en mémoire comme k1. Le résultat de la division de la valeur entièrement sélectionnée par trois M = √N / 3 - rappelez-vous le coefficient de mise à l'échelle PFT.
   
3. On obtient la valeur de la deuxième étape k ₂ , selon la règle du triangle égyptien, k ₂ = 4 ∙ M.
   
4. Nous trouvons la valeur de l'hypoténuse g = 5 ∙ M , et la valeur x ₁ = g doit être divisée par le nombre cinq. Comme vous pouvez le voir, la valeur de l'hypoténuse est toujours égale au nombre horizontal avec PFT.
   
5. Trouvez la coordonnée x ₁ = g .
   
6. Après cela, nous déterminons l'inflexion (dernier chiffre) du nombre N , φ = N (mod10) .
   
7. Nous trouvons le centre du losange le plus proche de k1 , puis examinons les losanges adjacents dans l'une des bandes de losanges (il y a 4 directions) pour trouver une solution.
   
8. Selon le type d'inflexion que nous obtenons au paragraphe 6, nous utilisons la colonne (masque) souhaitée parmi celles présentées dans le tableau. 1 pour déterminer les coordonnées du point de recherche ( x _1p , x _0p ) et trouver la valeur du nombre dans cette cellule N _p . Dans chaque losange, seules 4 cellules sont contrôlées à partir de la 41e cellule.
   
9. Après avoir établi que le nombre N appartient à un losange particulier et à une cellule, basé sur le même tableau. 1 on obtient les coordonnées planes N: (x _1p , x _0p ) .
   
10. Utilisation des propriétés du modèle mathématique sélectionné
    N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p ∙ q
    nous obtenons la représentation multiplicative de N à partir de l'additif.
    
11. Ainsi, en sortie de l'algorithme, on a: N = p ∙ q . En fonction de la valeur de flexion f selon les formules du tableau. 1, les coordonnées du point (x _1p , x _0p ) sont _{déterminées} et la différence ∆ = N (x _1p , x _0p ) - N (x ₁ , x ₀ ) est calculée. Si ∆ ≠ 0 , passez à une autre cellule, si toutes les cellules du losange sont cochées, puis à un autre losange.
    Si Δ = 0 , alors x ₁ = x _1p , x ₀ = x _0p et p = (x ₁ - x ₀ ) , q = N / p = (x ₁ + x ₀ ) .
    

Exemple 2. Étant donné: N = 1037 , un nombre d'une capacité de 4. Il est nécessaire de le factoriser. Nous agissons selon l'algorithme donné.

1. Nous extrayons la racine de N : √N = 32.202 . On arrondit : √N = 32 .
2. Nous vérifions si 32 est divisible par 3. Puisque 32 n'est pas divisible par 3, nous soustrayons 2. Donc, nous supposons que la première étape est k ₁ = 3 ∙ 10 = 30 , ici M = 10 = 30/3 est le facteur d'échelle PFT .
3. On obtient la valeur de la seconde étape k ₂ = 4 ∙ 10 = 40 .
4. On trouve la valeur de l'hypoténuse g = (k ² ₁ + k ² ₂ ) ^0,5 , à condition qu'elle soit divisée par 5, (30 ² +40 ² ) ^0,5 = 50.
5. Ainsi, x1 = k1 = 50 et le PFT se transforme en la forme g = 50 , k ₁ = 30, k ₂ = 40 .
6. Nous trouvons l'inflexion du nombre N : φ (1037) = 1037 (mod10) = 7 .
7. Nous trouvons le centre du losange le plus proche de N = 1037 .
   Il aura les coordonnées de la cellule centrale du losange: x ₁ = 50, x ₀ = 35 . La première coordonnée est le numéro de ligne contenant le CFT. Le carré de la plus petite jambe est 900, il est contenu dans la verticale avec le numéro 40. La cellule avec le numéro 957 se terminant par les sept les plus proches de 900 se trouve dans l'horizontale précédente avec le numéro 49 et dans la verticale avec le numéro 38. C'est le plus petit nombre de 4 dans le losange et avec flexion 7. Ici, nous utilisons les données du tableau 1. Le centre le plus proche du losange doit être trois cellules à gauche, c'est-à-dire qu'il appartient à la verticale 38-3 = 35, c'est la deuxième coordonnée du centre du losange. La valeur du nombre dans la cellule du centre du losange est N (50, 35) = 1275
   
   Il s'agit d'un losange ayant des carrés de pattes k ₁ et k ₂ à ses bords. Dans ce losange, min est un nombre se terminant par sept 957 dans une cellule ( x ₁ = 49, x ₀ = 38 ), et un autre nombre dans cette verticale se terminant en 7e 1157 , les grands nombres 1377 et 1577 se trouvent à gauche de la cellule centrale, coïncidant avec le nombre N = 1037 non, par conséquent, il est nécessaire de remonter vers le losange vers la gauche et plus haut avec la valeur dans la cellule centrale 1125 et avec les coordonnées de la cellule centrale ( x ₁ = 50 - 5 = 45, x ₀ = 35 - 5 = 30 ) Vérifiez les quatre nombres pour la flexion 7 Ce sont 847, 1027, 1207 et 1387 et il n'y a pas de coïncidences avec N = 1037 dans ce losange), nous augmenterons encore plus dans la même direction le long de la bande de losanges NW. La cellule centrale du nouveau losange a une valeur de 975 et des coordonnées ( x ₁ = 45 -5 = 40, x ₀ = 35 - 5 = 25 ). Nous vérifions dans ce losange les quatre nombres pour l'inflexion 7. C'est 737, 897, 1197 et finalement nous obtenons 1037 dans la cellule ( x _1p = 39, x _0p = 22 ), nous avons obtenu une correspondance complète avec le N. donné
   
   En détail, ces actions sont représentées par les calculs suivants: Conformément au tableau 1, nous calculons les coordonnées des cellules et leurs valeurs numériques. Après cela, nous trouvons les différences entre les valeurs calculées et données de N. Dans le premier losange, les 4 cellules sont calculées.
   
   ∆ = N (x _1c -1, x _0c -3) - N (x ₁ , x ₀ ) = N (49,32) - 1037 = 1377 - 1037 = 340 ≠ 0,
   ∆ = N (x _1c +1, x _0c -3) - N (x ₁ , x ₀ ) = N (51,32) - 1037 = 1577 - 1037 = 540 ≠ 0,
   ∆ = N (x _1c +1, x _0c +3) - N (x ₁ , x ₀ ) = N (51,38) - 1037 = 1157 - 1037 = 120 ≠ 0,
   ∆ = N (x _1c -1, x _0c +3) - N (x ₁ , x ₀ ) = N (49,38) - 1037 = 957 - 1037 = - 80 ≠ 0.
   Dans ce losange, il n'y a pas de coïncidence du nombre N avec les nombres dans les cellules.
   
   Nous allons au losange suivant avec le centre dans la cellule (x _1c -5, x _0c -5) = (45, 30) et la valeur qu'il _contient N (x _1c -5, x _0c -5) = N (45, 30) = 1125 .
   ∆ = N (x _1ts -1, x _0ts -3) - N (x ₁ , x ₀ ) = N (44,27) - 1037 = 1207 - 1037 = 170 ≠ 0,
   ∆ = N (x _1c +1, x _0c -3) - N (x ₁ , x ₀ ) = N (46,27) - 1037 = 1387 - 1037 = 350 ≠ 0,
   ∆ = N (x _1c +1, x _0c +3) - N (x ₁ , x ₀ ) = N (46,33) - 1037 = 1027 - 1037 = - 10 ≠ 0,
   ∆ = N (x _1c -1, x _0c +3) - N (x ₁ , x ₀ ) = N (44,33) - 1037 = 847 - 1037 = - 190 ≠ 0.
   Dans ce losange, il n'y a pas non plus de coïncidence du nombre N avec les nombres dans les cellules.
   
   Nous allons au losange suivant avec le centre dans la cellule (x _1c -5, x _0c -5) = (40, 25) et la valeur qu'il _contient N (x _1c -5, x _0c -5) = N (40, 25) = 975
   ∆ = N (x _1c -1, x _0c -3) - N (x ₁ , x ₀ ) = N (39,22) - 1037 = 1037 - 1037 = 0.
   Vous avez une différence de valeurs nulle. Il y a une coïncidence complète. Il en résulte que le nombre donné N (x ₁ , x ₀ ) = 1037 est contenu dans la cellule avec les coordonnées (x ₁ , x ₀ ) = (39, 22). Enfin, la solution du HFBC est déterminée par la relation de base ^{2 ±} - du modèle
   N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = (39 - 22) (39 + 22) = p ∙ q = 17 ∙ 61 .
   
8. Vous pouvez agir différemment en commençant par le losange indiqué au paragraphe 6, en utilisant le tableau. 1, nous découvrons si le nombre N appartient à un losange particulier, se déplaçant entre les centres des losanges d'abord horizontalement, vers la diagonale principale, puis descendant vers la prochaine bande de losanges et répétant tout à nouveau.
9. Après avoir établi que le nombre N appartient à un certain losange (dans notre cas, le losange aura des coordonnées ( x ₁ = 40, x ₀ = 25 )) sur la base du même tableau. 1 on obtient les coordonnées N : x _1p = 39 , x _2p = 22 (9 losanges vus).
10. Utilisation des propriétés du modèle mathématique sélectionné du nombre
    N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p ∙ q
    nous obtenons la représentation multiplicative de N à partir de l'additif:
    N = (39 - 22) (39 + 22) = 17 ∙ 61 = 1037 .

Ainsi, à la sortie, nous avons N = p · q = 17 · 61 = 1037 , c'est-à-dire que la solution au problème a été obtenue avec succès.

Nous obtenons également le résultat d'une solution logicielle au problème de l'exemple 3.

Exemple 3 . Donné: N = 3808572773, un nombre avec une résolution de 10.

1. Nous extrayons la racine de N: √N = 61713 , 64 = 61713 .
2. Nous vérifions si 61713 est divisible par 3. Puisque 61713 est divisible par 3,
   6 + 1 + 7 + 1 + 3 = 18 est divisible par 3, la première étape k ₁ est égale à k ₁ = 61713 .
3. k ₂ = 4k ₁ /3 => 4k ₂ /3 = 82284 .
4. g =√k ₁₂ +k ₂₂ , ,
   5 · g = √617132 + 822842 = 102855 .
5. x ₁ = k ₁ = 61713 , k ₁ = 61713, k ₂ = 82284, g = 102855 .
6. N: (3808572773) = 3808572773(mod10) = 3 .
7. . x ₁ = 61715; x ₉ = 0 .
8. , 7, . 1, N , , , , .
9. N ( x ₁ = 62015 , x ₀ = 6085 ) N :
   x _1p = 62013; x _0p = 6086 ; ( 60 ).
10. 
    N = x ² ₁ — x ² ₀ = (x ₁ — x ₀ )(x ₁ + x ₀ ) =p ·q N :
    N = (62013 — 6086) · (62013 + 62086) = 55927 · 68099 = 3808572773 ;
11. , N = p · q = 55927 · 68099 = 3808572773 , . . .