Imaginez que vous devez générer un nombre aléatoire uniformément réparti de 1 à 10. C'est-à-dire un entier de 1 à 10 inclus, avec une probabilité égale (10%) de chaque occurrence. Mais, disons, sans accès aux pièces de monnaie, aux ordinateurs, aux matières radioactives ou à d'autres sources similaires de nombres (pseudo) aléatoires. Vous n'avez qu'une chambre avec des gens.

Supposons qu'il y ait un peu plus de 8500 étudiants dans cette salle.

La chose la plus simple est de demander à quelqu'un: "Hé, choisissez un nombre aléatoire de un à dix!". L'homme répond: "Sept!". Super! Vous avez maintenant un numéro. Cependant, vous commencez à vous demander s'il est réparti également.

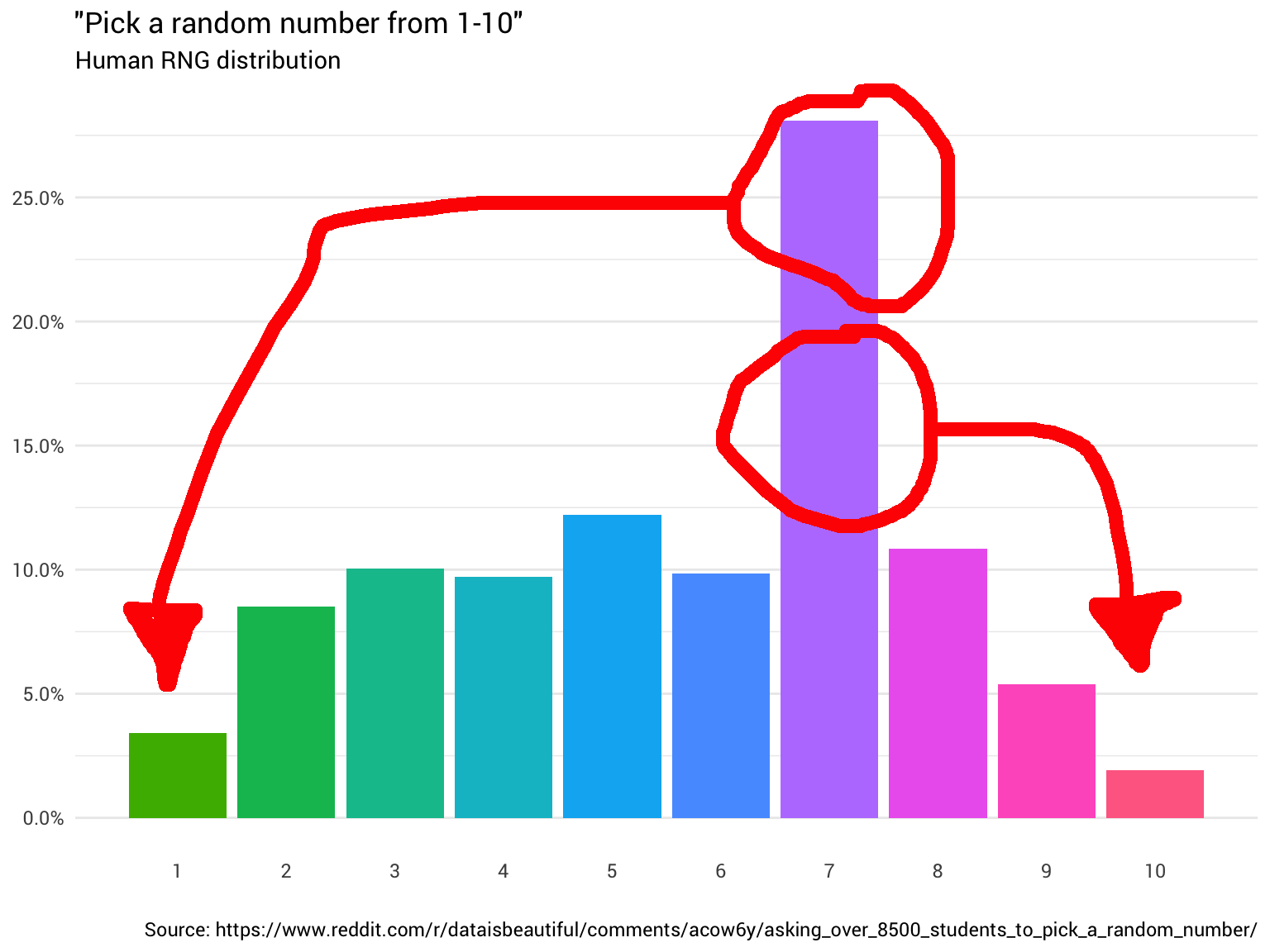
Vous avez donc décidé de demander à quelques personnes de plus. Vous continuez à leur demander et à compter leurs réponses, en arrondissant les nombres fractionnaires et en ignorant ceux qui pensent que la plage de 1 à 10 inclut 0. En fin de compte, vous commencez à voir que la distribution n'est même pas du tout:

library(tidyverse) probabilities <- read_csv("https://git.io/fjoZ2") %>% count(outcome = round(pick_a_random_number_from_1_10)) %>% filter(!is.na(outcome), outcome != 0) %>% mutate(p = n / sum(n)) probabilities %>% ggplot(aes(x = outcome, y = p)) + geom_col(aes(fill = as.factor(outcome))) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = '"Pick a random number from 1-10"', subtitle = "Human RNG distribution", x = "", y = NULL, caption = "Source: https://www.reddit.com/r/dataisbeautiful/comments/acow6y/asking_over_8500_students_to_pick_a_random_number/") 

Données de Reddit

Vous vous frappez le front. Bien sûr , ce ne sera pas aléatoire. Après tout, vous ne pouvez pas faire confiance aux gens .

Alors que faire?

J'aimerais pouvoir trouver une fonction qui transforme la distribution du «RNG humain» en une distribution uniforme ...

L'intuition est ici relativement simple. Il vous suffit de prendre la masse de distribution d'où elle est supérieure à 10% et de la déplacer vers où elle est inférieure à 10%. Pour que toutes les colonnes du graphique soient au même niveau:



En théorie, une telle fonction devrait exister. En fait, il doit y avoir de nombreuses fonctions différentes (pour la permutation). Dans un cas extrême, vous pouvez «couper» chaque colonne en blocs infiniment petits et créer une distribution de n'importe quelle forme (comme les briques Lego).

Bien sûr, un exemple aussi extrême est un peu lourd. Idéalement, nous voulons conserver autant que possible la distribution initiale (c'est-à-dire, faire le moins de lambeaux et de mouvements possible).

Comment trouver une telle fonction?

Eh bien, notre explication ci-dessus ressemble beaucoup à une programmation linéaire . De Wikipédia:

La programmation linéaire (LP, également appelée optimisation linéaire) est une méthode pour obtenir le meilleur résultat ... dans un modèle mathématique dont les exigences sont représentées par des relations linéaires ... La forme standard est la forme habituelle et la plus intuitive de décrire un problème de programmation linéaire. Il se compose de trois parties:

• Fonction linéaire à maximiser
  
• Limitations du problème du formulaire suivant
  
• Variables non négatives

De même, le problème de la redistribution peut être formulé.

Présentation du problème

Nous avons un ensemble de variables $$$(x_ {i, j}$ , dont chacun code une fraction de la probabilité redistribuée à partir d'un entier $$$i$ (1 à 10) à un entier $$$j$ (de 1 à 10). Par conséquent, si $$$(x_ {7,1} = 0,2$ , nous devons ensuite transférer 20% des réponses de sept à une.

 variables <- crossing(from = probabilities$outcome, to = probabilities$outcome) %>% mutate(name = glue::glue("x({from},{to})"), ix = row_number()) variables 

  ## # A tibble: 100 x 4
 ## de à nommer ix
 ## <dbl> <dbl> <glue> <int>
 ## 1 1 1 x (1,1) 1
 ## 2 1 2 x (1,2) 2
 ## 3 1 3 x (1,3) 3
 ## 4 1 4 x (1,4) 4
 ## 5 1 5 x (1,5) 5
 ## 6 1 6 x (1,6) 6
 ## 7 1 7 x (1,7) 7
 ## 8 1 8 x (1,8) 8
 ## 9 1 9 x (1,9) 9
 ## 10 1 10 x (1,10) 10
 ## # ... avec 90 lignes supplémentaires 

Nous voulons limiter ces variables afin que toutes les probabilités redistribuées totalisent jusqu'à 10%. En d'autres termes, pour chaque $$$j$ de 1 à 10:

$$

$$x_ {1, j} + x_ {2, j} + \ ldots \ x_ {10, j} = 0,1$$

Nous pouvons représenter ces restrictions comme une liste de tableaux dans R. Plus tard, nous les lions dans une matrice.

 fill_array <- function(indices, weights, dimensions = c(1, max(variables$ix))) { init <- array(0, dim = dimensions) if (length(weights) == 1) { weights <- rep_len(1, length(indices)) } reduce2(indices, weights, function(a, i, v) { a[1, i] <- v a }, .init = init) } constrain_uniform_output <- probabilities %>% pmap(function(outcome, p, ...) { x <- variables %>% filter(to == outcome) %>% left_join(probabilities, by = c("from" = "outcome")) fill_array(x$ix, x$p) }) 

Nous devons également nous assurer que toute la masse des probabilités de la distribution initiale est préservée. Donc pour tout le monde $$$j$ dans la plage de 1 à 10:

$$

$$x_ {1, j} + x_ {2, j} + \ ldots \ x_ {10, j} = 0,1$$

 one_hot <- partial(fill_array, weights = 1) constrain_original_conserved <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome) %>% pull(ix) %>% one_hot() }) 

Comme déjà mentionné, nous voulons maximiser la préservation de la distribution d'origine. C'est notre objectif :

$$

$$maximiser (x_ {1, 1} + x_ {2, 2} + \ ldots \ x_ {10, 10})$$

 maximise_original_distribution_reuse <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome, to == outcome) %>% pull(ix) %>% one_hot() }) objective <- do.call(rbind, maximise_original_distribution_reuse) %>% colSums() 

Ensuite, nous passons le problème au solveur, par exemple, le package lpSolve dans R, combinant les contraintes créées dans une matrice:

 # Make results reproducible... set.seed(23756434) solved <- lpSolve::lp( direction = "max", objective.in = objective, const.mat = do.call(rbind, c(constrain_original_conserved, constrain_uniform_output)), const.dir = c(rep_len("==", length(constrain_original_conserved)), rep_len("==", length(constrain_uniform_output))), const.rhs = c(rep_len(1, length(constrain_original_conserved)), rep_len(1 / nrow(probabilities), length(constrain_uniform_output))) ) balanced_probabilities <- variables %>% mutate(p = solved$solution) %>% left_join(probabilities, by = c("from" = "outcome"), suffix = c("_redistributed", "_original")) 

La redistribution suivante est renvoyée:

 library(gganimate) redistribute_anim <- bind_rows(balanced_probabilities %>% mutate(key = from, state = "Before"), balanced_probabilities %>% mutate(key = to, state = "After")) %>% ggplot(aes(x = key, y = p_redistributed * p_original)) + geom_col(aes(fill = as.factor(from)), position = position_stack()) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = 'Balancing the "Human RNG distribution"', subtitle = "{closest_state}", x = "", y = NULL) + transition_states( state, transition_length = 4, state_length = 3 ) + ease_aes('cubic-in-out') animate( redistribute_anim, start_pause = 8, end_pause = 8 ) 

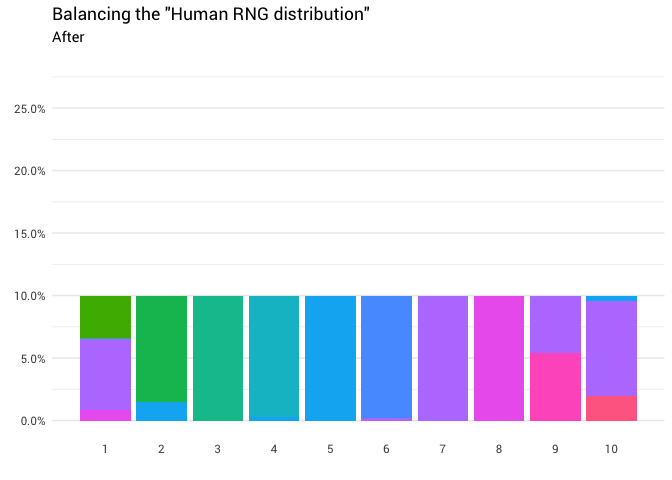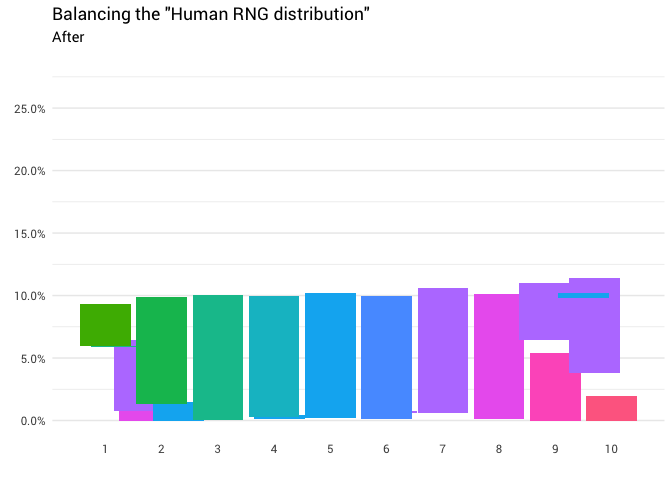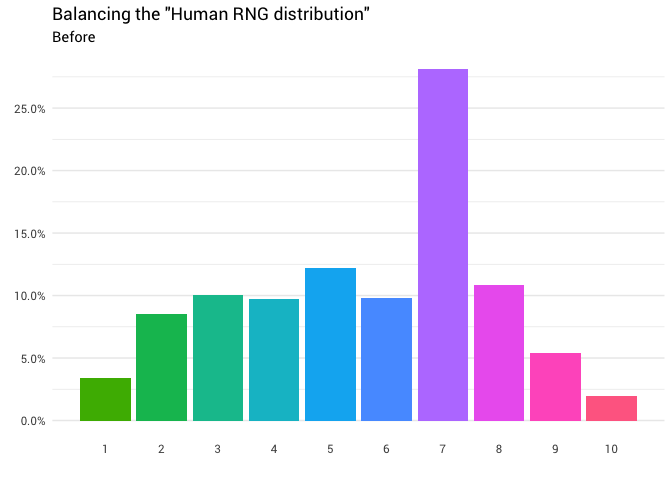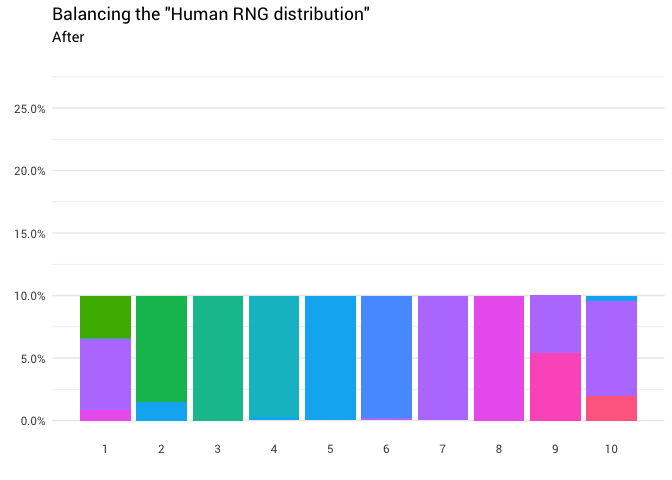
Super! Nous avons maintenant une fonction de redistribution. Examinons de plus près comment la masse se déplace:

 balanced_probabilities %>% ggplot(aes(x = from, y = to)) + geom_tile(aes(alpha = p_redistributed, fill = as.factor(from))) + geom_text(aes(label = ifelse(p_redistributed == 0, "", scales::percent(p_redistributed, 2)))) + scale_alpha_continuous(limits = c(0, 1), range = c(0, 1)) + scale_fill_discrete(h = c(120, 360)) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(breaks = 1:10) + theme_minimal(base_family = "Roboto") + theme(panel.grid.minor = element_blank(), panel.grid.major = element_line(linetype = "dotted"), legend.position = "none") + labs(title = "Probability mass redistribution", x = "Original number", y = "Redistributed number") 

Ce graphique indique que dans environ 8% des cas où quelqu'un appelle huit comme un nombre aléatoire, vous devez prendre la réponse comme une unité. Dans les 92% de cas restants, il reste le huitième.

Il serait assez simple de résoudre le problème si nous avions accès à un générateur de nombres aléatoires uniformément répartis (de 0 à 1). Mais nous n'avons qu'une salle pleine de monde. Heureusement, si vous êtes prêt à accepter quelques inexactitudes mineures, vous pouvez faire un assez bon RNG avec des gens sans demander plus de deux fois.

Pour revenir à notre distribution d'origine, nous avons les probabilités suivantes pour chaque nombre, qui peuvent être utilisées pour réattribuer une probabilité, si nécessaire.

 probabilities %>% transmute(number = outcome, probability = scales::percent(p)) 

  ## # A tibble: 10 x 2
 ## probabilité de nombre
 ## <dbl> <chr>
 ## 1 1 3,4%
 ## 2 2 8,5%
 ## 3 3 10,0%
 ## 4 4 9,7%
 ## 5 5 12,2%
 ## 6 6 9,8%
 ## 7 7 28,1%
 ## 8 8 10,9%
 ## 9 9 5,4%
 ## 10 10 1,9% 

Par exemple, lorsque quelqu'un nous donne huit comme nombre aléatoire, nous devons déterminer si ces huit doivent devenir une unité ou non (probabilité 8%). Si nous demandons à une autre personne un nombre aléatoire, alors avec une probabilité de 8,5%, elle répondra «deux». Donc, si ce deuxième nombre est 2, nous savons que nous devons retourner 1 comme un nombre aléatoire uniformément distribué .

En étendant cette logique à tous les nombres, nous obtenons l'algorithme suivant:

• Demandez à une personne un nombre aléatoire, $$$n_1$ .
• $$$n_1 = 1, 2, 3, 4, 6, 9,$ ou $$ :
  
  • Votre numéro aléatoire $$$n_1$
• Si $$$n_1 = 5$ :
  
  • Demandez à une autre personne un nombre aléatoire ( $$$n_2$ )
  • Si $$$n_2 = 5$ (12,2%):
    
    • Votre numéro aléatoire 2
  • Si $$$n_2 = 10$ (1,9%):
    
    • Votre numéro aléatoire 4
  • Sinon, votre nombre aléatoire est 5
• Si $$$n_1 = 7$ :
  
  • Demandez à une autre personne un nombre aléatoire ( $$$n_2$ )
  • Si $$$n_2 = 2$ ou $$ (20,7%):
    
    • Votre numéro aléatoire 1
  • Si $$$n_2 = 8$ ou $$ (16,2%):
    
    • Votre nombre aléatoire est 9
  • Si $$$n_2 = 7$ (28,1%):
    
    • Votre nombre aléatoire est 10
  • Sinon, votre nombre aléatoire est 7
• Si $$$n_1 = 8$ :
  
  • Demandez à une autre personne un nombre aléatoire ( $$$n_2$ )
  • Si $$$n_2 = 2$ (8,5%):
    
    • Votre numéro aléatoire 1
  • Sinon, votre nombre aléatoire est 8

En utilisant cet algorithme, vous pouvez utiliser un groupe de personnes pour obtenir quelque chose près d'un générateur de nombres aléatoires uniformément répartis de 1 à 10!