Empiriquement, nous avons vu que la régularisation permet de réduire la reconversion. C'est inspirant - mais, malheureusement, il n'est pas évident pourquoi la régularisation aide. Habituellement, les gens l'expliquent d'une certaine manière: dans un sens, les poids plus petits ont moins de complexité, ce qui fournit une explication plus simple et plus efficace des données, donc elles devraient être préférées. Cependant, cette explication est trop courte et certaines parties peuvent sembler douteuses ou mystérieuses. Déplions cette histoire et examinons-la d'un œil critique. Pour ce faire, supposons que nous ayons un ensemble de données simple pour lequel nous voulons créer un modèle:

En termes de signification, nous étudions ici le phénomène du monde réel, et x et y désignent des données réelles. Notre objectif est de construire un modèle qui nous permette de prédire y en fonction de x. Nous pourrions essayer d'utiliser un réseau de neurones pour créer un tel modèle, mais je suggère quelque chose de plus simple: je vais essayer de modéliser y comme un polynôme en x. Je le ferai à la place des réseaux de neurones, car l'utilisation de polynômes rend l'explication particulièrement claire. Dès que nous traiterons du cas du polynôme, nous passerons à l'Assemblée nationale. Il y a dix points sur le graphique ci-dessus, ce qui signifie que nous pouvons
trouver un polynôme unique du 9ème ordre y = a
0 x
9 + a
1 x
8 + ... + a
9 qui correspond exactement aux données. Et voici le graphique de ce polynôme.
Coup parfait. Mais nous pouvons obtenir une bonne approximation en utilisant le modèle linéaire y = 2x
Lequel est le meilleur? Quel est le plus susceptible d'être vrai? Lequel sera mieux généralisé à d'autres exemples du même phénomène du monde réel?
Des questions difficiles. Et on ne peut y répondre exactement sans informations supplémentaires sur le phénomène sous-jacent du monde réel. Cependant, regardons deux possibilités: (1) un modèle avec un polynôme du 9ème ordre décrit vraiment le phénomène du monde réel, et donc, se généralise parfaitement; (2) le modèle correct est y = 2x, mais nous avons un bruit supplémentaire associé à l'erreur de mesure, donc le modèle ne s'adapte pas parfaitement.
A priori, on ne peut dire laquelle des deux possibilités est correcte (ou qu'il n'y en a pas de troisième). Logiquement, n'importe lequel d'entre eux peut s'avérer vrai. Et la différence entre eux n'est pas anodine. Oui, sur la base des données disponibles, on peut dire qu'il n'y a qu'une légère différence entre les modèles. Mais supposons que nous voulons prédire la valeur de y correspondant à une grande valeur de x, beaucoup plus grande que n'importe laquelle de celles montrées dans le graphique. Si nous essayons de le faire, une énorme différence apparaîtra entre les prédictions des deux modèles, car le terme x
9 domine dans le polynôme du 9ème ordre, et le modèle linéaire reste linéaire.
Un point de vue sur ce qui se passe est de déclarer qu'une explication plus simple devrait être utilisée en science, si possible. Lorsque nous trouvons un modèle simple qui explique de nombreux points de référence, nous voulons juste crier: "Eurêka!" Après tout, il est peu probable qu'une explication simple apparaisse purement par accident. Nous pensons que le modèle devrait produire une certaine vérité associée au phénomène. Dans ce cas, le modèle y = 2x + bruit semble beaucoup plus simple que y = a
0 x
9 + a
1 x
8 + ... Il serait surprenant que la simplicité apparaisse par hasard, nous soupçonnons donc que le bruit y = 2x + exprime certains vérité sous-jacente. De ce point de vue, le modèle du 9e ordre étudie simplement l'effet du bruit local. Bien que le modèle du 9e ordre fonctionne parfaitement pour ces points de référence spécifiques, il ne peut pas se généraliser à d'autres points, ce qui permet au modèle linéaire avec bruit d'avoir de meilleures capacités de prédiction.
Voyons ce que ce point de vue signifie pour les réseaux de neurones. Supposons que, dans notre réseau, il y ait principalement des poids faibles, comme c'est généralement le cas dans les réseaux régularisés. En raison de son faible poids, le comportement du réseau ne change pas beaucoup lorsque plusieurs entrées aléatoires sont modifiées ici et là. En conséquence, le réseau régularisé est difficile à apprendre les effets du bruit local présent dans les données. Cela est similaire à la volonté de s'assurer que les preuves individuelles n'affectent pas considérablement la sortie du réseau dans son ensemble. Au lieu de cela, le réseau régularisé est formé pour répondre aux preuves que l'on trouve souvent dans les données de formation. Inversement, un réseau avec des poids importants peut changer son comportement assez fortement en réponse à de petits changements dans les données d'entrée. Par conséquent, un réseau irrégulier peut utiliser des poids importants pour former un modèle complexe qui contient beaucoup d'informations sur le bruit dans les données d'entraînement. En bref, les limites des réseaux régularisés leur permettent de créer des modèles relativement simples basés sur des modèles que l'on trouve souvent dans les données d'entraînement, et ils résistent aux écarts causés par le bruit dans les données d'entraînement. On espère que cela permettra à nos réseaux d'étudier le phénomène lui-même et de mieux généraliser les connaissances acquises.
Cela dit, l'idée de privilégier des explications plus simples devrait vous rendre nerveux. Parfois, les gens appellent cette idée «le rasoir d'Occam» et l'appliquent avec zèle, comme si elle avait le statut d'un principe scientifique général. Mais ce n'est bien sûr pas un principe scientifique général. Il n'y a aucune raison a priori logique de préférer des explications simples à des explications complexes. Parfois, une explication plus compliquée est correcte.
Permettez-moi de décrire deux exemples de la façon dont une explication plus complexe s'est avérée correcte. Dans les années 40, le physicien Marcel Shane a annoncé la découverte d'une nouvelle particule. L'entreprise pour laquelle il travaillait, General Electric, était ravie et a largement diffusé la publication de cet événement. Cependant, le physicien Hans Bethe était sceptique. Bethe a visité Shane et a étudié les plaques avec des traces de la nouvelle particule de Shane. Shane a montré Beta plaque après plaque, mais Bete a trouvé sur chacun d'eux un problème qui indiquait la nécessité de refuser ces données. Enfin, Shane a montré à Beta un record qui semblait en forme. Bethe a dit que c'était probablement juste une déviation statistique. Shane: "Oui, mais les chances que cela soit dû aux statistiques, même selon votre propre formule, sont de un sur cinq." Bethe: "Cependant, j'ai déjà regardé cinq disques." Enfin, Shane a déclaré: "Mais vous avez expliqué chacun de mes enregistrements, chaque bonne image avec une autre théorie, et j'ai une hypothèse qui explique tous les enregistrements à la fois, d'où il résulte que nous parlons d'une nouvelle particule." Bethe a répondu: «La seule différence entre mes explications et les vôtres est que les vôtres ont tort et les miennes sont correctes. Votre seule explication est incorrecte et toutes mes explications sont correctes. » Par la suite, il s'est avéré que la nature était d'accord avec Bethe, et la particule de Shane s'est évaporée.
Dans le deuxième exemple, en 1859, l’astronome Urbain Jean Joseph Le Verrier a découvert que la forme de l’orbite de Mercure ne correspond pas à la théorie de Newton de la gravitation universelle. Il y avait un petit écart par rapport à cette théorie, puis plusieurs options pour résoudre le problème ont été proposées, ce qui se résumait au fait que la théorie de Newton dans son ensemble est correcte et ne nécessite qu'un léger changement. Et en 1916, Einstein a montré que cette déviation peut être bien expliquée en utilisant sa théorie générale de la relativité, radicalement différente de la gravité newtonienne et basée sur des mathématiques beaucoup plus complexes. Malgré cette complexité supplémentaire, il est généralement admis aujourd'hui que l'explication d'Einstein est correcte, et la gravité newtonienne est incorrecte
même sous une forme modifiée . Cela se produit, en particulier, parce que nous savons aujourd'hui que la théorie d'Einstein explique de nombreux autres phénomènes avec lesquels la théorie de Newton a eu des difficultés. De plus, encore plus étonnant, la théorie d'Einstein prédit avec précision plusieurs phénomènes que la gravité newtonienne ne prédisait pas du tout. Cependant, ces qualités impressionnantes n'étaient pas évidentes dans le passé. A en juger par la simple simplicité, une forme modifiée de la théorie newtonienne aurait alors semblé plus attrayante.
Trois morales peuvent être tirées de ces histoires. Premièrement, il est parfois assez difficile de décider laquelle des deux explications sera «la plus facile». Deuxièmement, même si nous avons pris une telle décision, la simplicité doit être guidée avec beaucoup de prudence! Troisièmement, le véritable test du modèle n'est pas la simplicité, mais la qualité avec laquelle il prédit de nouveaux phénomènes dans de nouvelles conditions de comportement.
Compte tenu de tout cela et en faisant attention, nous accepterons un fait empirique - les SN régularisées sont généralement mieux généralisées que les SN irrégulières. Par conséquent, plus tard dans le livre, nous utiliserons souvent la régularisation. Les histoires mentionnées ne sont nécessaires que pour expliquer pourquoi personne n'a encore développé une explication théorique complètement convaincante de la raison pour laquelle la régularisation aide les réseaux à se généraliser. Les chercheurs continuent de publier des travaux où ils essaient d'essayer différentes approches de la régularisation, de les comparer, d'examiner ce qui fonctionne le mieux et d'essayer de comprendre pourquoi différentes approches fonctionnent plus ou moins bien. La régularisation peut donc être traitée comme un
nuage . Quand cela aide assez souvent, nous n'avons pas une compréhension systémique complètement satisfaisante de ce qui se passe - seulement des règles heuristiques et pratiques incomplètes.
Ici se trouve un ensemble plus profond de problèmes qui vont au cœur même de la science. Il s'agit d'un problème de généralisation. La régularisation peut nous donner une baguette magique de calcul qui aide nos réseaux à mieux généraliser les données, mais elle ne donne pas une compréhension de base du fonctionnement de la généralisation et de la meilleure approche.
Ces problèmes remontent au
problème de l'induction , dont une interprétation bien connue a été réalisée par le philosophe écossais
David Hume dans le livre "
A Study on Human Cognition " (1748). Le problème d'induction fait l'objet du «
théorème sur l'absence de repas gratuits » de
David Walpert et William Macredie (1977).
Et cela est particulièrement ennuyeux, car dans la vie ordinaire, les gens sont phénoménalement bien capables de généraliser des données. Montrez quelques images de l'éléphant à l'enfant, et il apprendra rapidement à reconnaître d'autres éléphants. Bien sûr, il peut parfois faire une erreur, par exemple, confondre un rhinocéros avec un éléphant, mais en général, ce processus fonctionne de manière étonnamment précise. Maintenant, nous avons un système - le cerveau humain - avec une énorme quantité de paramètres libres. Et après avoir vu une ou plusieurs images d'entraînement, le système apprend à les généraliser à d'autres images. Notre cerveau, dans un sens, est incroyablement bon pour régulariser! Mais comment fait-on cela? Pour le moment, cela nous est inconnu. Je pense qu'à l'avenir, nous développerons des technologies de régularisation plus puissantes dans les réseaux de neurones artificiels, des techniques qui permettront finalement à l'Assemblée nationale de généraliser des données basées sur des ensembles de données encore plus petits.
En fait, nos réseaux se généralisent déjà beaucoup mieux que ce à quoi on pourrait s'attendre a priori. Un réseau de 100 neurones cachés a près de 80 000 paramètres. Nous n'avons que 50 000 images dans les données d'entraînement. Cela revient à essayer d'étirer un polynôme de 80 000 ordres sur 50 000 points de référence. De toute évidence, notre réseau doit se recycler terriblement. Et pourtant, comme nous l'avons vu, un tel réseau se généralise en fait assez bien. Pourquoi cela se produit-il? Ce n'est pas tout à fait clair. Il a été
émis l'hypothèse que «la dynamique de l'apprentissage par descente de gradient dans les réseaux multicouches est soumise à l'autorégulation». C'est une fortune extrême, mais aussi un fait assez inquiétant, car on ne comprend pas pourquoi cela se produit. Entre-temps, nous adopterons une approche pragmatique et nous recourrons à la régularisation dans la mesure du possible. Cela sera bénéfique pour notre Assemblée nationale.
Permettez-moi de terminer cette section en revenant à ce que je n'ai pas expliqué auparavant: que la régularisation de L2 ne limite pas les déplacements. Naturellement, il serait facile de changer la procédure de régularisation pour régulariser les déplacements. Mais empiriquement, cela ne change souvent pas les résultats de manière notable, donc, dans une certaine mesure, traiter la régularisation des biais, ou non, est une question d'accord. Cependant, il convient de noter qu'un grand déplacement ne rend pas un neurone sensible aux entrées comme les gros poids. Par conséquent, nous n'avons pas à nous soucier des décalages importants qui permettent à nos réseaux d'apprendre le bruit dans les données d'entraînement. En même temps, en permettant de grands déplacements, nous rendons nos réseaux plus flexibles dans leur comportement - en particulier, les grands déplacements facilitent la saturation des neurones, ce que nous souhaiterions. Pour cette raison, nous n'incluons généralement pas les compensations dans la régularisation.
Autres techniques de régularisation
Il existe de nombreuses techniques de régularisation en plus de L2. En fait, tant de techniques ont déjà été développées que, avec tout le désir, je ne pouvais pas toutes les décrire brièvement. Dans cette section, je décrirai brièvement trois autres approches pour réduire le recyclage: régulariser la L1,
abandonner et augmenter artificiellement l'ensemble de formation. Nous ne les étudierons pas aussi profondément que les sujets précédents. Au lieu de cela, nous apprenons à les connaître et apprécions en même temps la variété des techniques de régularisation existantes.
Régularisation L1
Dans cette approche, nous modifions la fonction de coût irrégulier en ajoutant la somme des valeurs absolues des poids:
Intuitivement, cela est similaire à la régularisation de L2, qui inflige des amendes pour les poids élevés et fait que le réseau préfère les poids faibles. Bien sûr, le terme de régularisation L1 n'est pas comme le terme de régularisation L2, vous ne devez donc pas vous attendre exactement au même comportement. Essayons de comprendre en quoi le comportement d'un réseau formé à la régularisation L1 diffère d'un réseau formé à la régularisation L2.
Pour ce faire, regardez les dérivées partielles de la fonction de coût. En différenciant (95), on obtient:
où sgn (w) est le signe de w, c'est-à-dire +1 si w est positif et -1 si w est négatif. En utilisant cette expression, nous modifions légèrement la propagation arrière afin qu'elle effectue une descente de gradient stochastique en utilisant la régularisation L1. La règle de mise à jour finale pour le réseau régularisé L1:
où, comme d'habitude, ∂C / ∂w peut éventuellement être estimé en utilisant la valeur moyenne du mini-paquet. Comparez cela avec la règle de mise à jour de régularisation L2 (93):
Dans les deux expressions, la régularisation a pour effet de réduire les poids. Cela coïncide avec la notion intuitive que les deux types de régularisation pénalisent les poids importants. Cependant, les poids sont réduits de différentes manières. Dans la régularisation de L1, les poids diminuent d'une valeur constante, tendant vers 0. Dans la régularisation de L2, les poids diminuent d'une valeur proportionnelle à w. Par conséquent, lorsqu'un poids a une grande valeur | w |, la régularisation de L1 réduit le poids pas autant que L2. Et vice versa, quand | w | petite, la régularisation de L1 réduit le poids beaucoup plus que la régularisation de L2. En conséquence, la régularisation de L1 a tendance à concentrer les pondérations du réseau dans un nombre relativement petit d'obligations de grande importance, tandis que les autres pondérations tendent à zéro.
J'ai légèrement lissé un problème dans la discussion précédente - la dérivée partielle ∂C / ∂w n'est pas définie lorsque w = 0. En effet, la fonction | w | il y a un «kink» aigu au point w = 0, il ne peut donc pas être différencié. Mais ce n'est pas effrayant. Nous appliquons simplement la règle irrégulière habituelle pour la descente de gradient stochastique lorsque w = 0. Intuitivement, il n'y a rien de mal à cela - la régularisation devrait réduire les poids, et évidemment elle ne peut pas réduire les poids déjà égaux à 0. Plus précisément, nous utiliserons les équations (96) et (97) à la condition que sgn (0) = 0. Cela nous donnera une règle pratique et compacte pour la descente de gradient stochastique avec régularisation L1.
Exception [abandon]
Une exception est une technique de régularisation complètement différente. Contrairement à la régularisation de L1 et L2, l'exception ne concerne pas un changement dans la fonction de coût. Au lieu de cela, nous changeons le réseau lui-même. Permettez-moi d'expliquer la mécanique de base du fonctionnement d'une exception avant d'aborder la question de savoir pourquoi cela fonctionne et avec quels résultats.
Supposons que nous essayons de former un réseau:
En particulier, supposons que nous ayons l'entrée d'apprentissage x et la sortie souhaitée correspondante y. Habituellement, nous l'entraînions en distribuant directement x sur le réseau, puis en nous propageant en retour pour déterminer la contribution du gradient. Une exception modifie ce processus. Nous commençons par supprimer aléatoirement et temporairement la moitié des neurones du réseau cachés, laissant les neurones d'entrée et de sortie inchangés. Après cela, nous aurons environ un tel réseau. Notez que les neurones exclus, ceux qui sont temporairement supprimés, sont toujours marqués dans le diagramme:
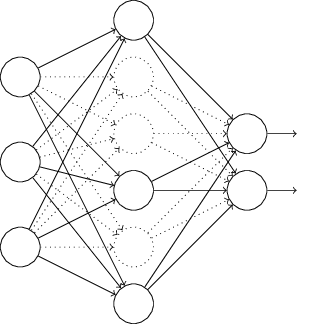
Nous passons x par distribution directe sur le réseau modifié, puis distribuons le résultat, également sur le réseau modifié. Après avoir fait cela avec un mini-package d'exemples, nous mettons à jour les poids et décalages correspondants. Ensuite, nous répétons ce processus, en restaurant d'abord les neurones exclus, puis en choisissant un nouveau sous-ensemble aléatoire de neurones cachés à supprimer, en évaluant le gradient pour un autre mini-paquet et en mettant à jour les poids et les décalages du réseau.
En répétant ce processus encore et encore, nous obtenons un réseau qui a appris certains poids et déplacements. Naturellement, ces poids et déplacements ont été appris dans des conditions dans lesquelles la moitié des neurones cachés étaient exclus.
Et lorsque nous lancerons le réseau dans son intégralité, nous aurons deux fois plus de neurones cachés actifs. Pour compenser cela, nous divisons par deux les poids provenant des neurones cachés.La procédure d'exclusion peut sembler étrange et arbitraire. Pourquoi devrait-elle aider à la régularisation? Pour expliquer ce qui se passe, je veux que vous oubliez l'exception pendant un certain temps et présentiez la formation de l'Assemblée nationale de manière standard. En particulier, imaginez que nous formons plusieurs NS différents en utilisant les mêmes données d'entraînement. Bien sûr, les réseaux peuvent varier au début, et parfois la formation peut produire des résultats différents. Dans de tels cas, nous pourrions appliquer une sorte de calcul de moyenne ou de vote pour décider lequel des résultats accepter. Par exemple, si nous avons formé cinq réseaux et que trois d'entre eux classent le nombre en «3», c'est probablement le vrai trois. Et les deux autres réseaux se trompent probablement. Un tel schéma de moyenne est souvent un moyen utile (quoique coûteux) de réduire le recyclage. La raison en estque différents réseaux peuvent se recycler de différentes manières, et la moyenne peut aider à éliminer ce recyclage.Comment tout cela se rapporte-t-il à l'exception? Heuristiquement, lorsque nous excluons différents ensembles de neutrons, c'est comme si nous formions différents NS. Par conséquent, la procédure d'exclusion est similaire à la moyenne des effets sur un très grand nombre de réseaux différents. Différents réseaux se recyclent de différentes manières, on espère donc que l'effet moyen de l'exclusion réduira le recyclage.Une explication heuristique connexe des avantages de l'exclusion est donnée dans l' un des premiers travauxen utilisant cette technique: «Cette technique réduit l'adaptation articulaire complexe des neurones, car le neurone ne peut pas compter sur la présence de certains voisins. En fin de compte, il doit apprendre des traits plus fiables qui peuvent être utiles pour travailler avec de nombreux sous-ensembles aléatoires différents de neurones. » En d'autres termes, si nous imaginons notre Assemblée nationale comme un modèle faisant des prédictions, alors une exception sera un moyen de garantir la stabilité du modèle à la perte de pièces individuelles de preuves. En ce sens, la technique ressemble aux régularisations de L1 et L2, qui cherchent à réduire les poids, et à rendre ainsi le réseau plus résistant à la perte de toute connexion individuelle dans le réseau.Naturellement, la véritable mesure de l'utilité de l'exclusion est son énorme succès dans l'amélioration de l'efficacité des réseaux de neurones. Dans l' œuvre originalelà où cette méthode a été introduite, elle a été appliquée à de nombreuses tâches différentes. Nous sommes particulièrement intéressés par le fait que les auteurs ont appliqué l'exception à la classification des nombres du MNIST, en utilisant un réseau de distribution directe simple similaire à celui que nous avons examiné. Le papier note que jusque-là, le meilleur résultat pour une telle architecture était une précision de 98,4%. Ils l'ont amélioré à 98,7% en utilisant une combinaison d'exclusion et une forme modifiée de régularisation L2. Des résultats tout aussi impressionnants ont été obtenus pour de nombreuses autres tâches, notamment la reconnaissance des formes et de la parole, et le traitement du langage naturel. L'exception a été particulièrement utile pour la formation de grands réseaux profonds, où le problème de la reconversion se pose souvent.Extension artificielle de l'ensemble de données de formation
Nous avons vu plus tôt que notre précision de classification MNIST a chuté à 80%, lorsque nous avons utilisé seulement 1 000 images d'entraînement. Et pas étonnant - avec moins de données, notre réseau rencontrera moins d'options pour écrire des nombres par des personnes. Essayons de former notre réseau de 30 neurones cachés, en utilisant différents volumes de l'ensemble d'entraînement pour étudier le changement d'efficacité. Nous nous entraînons en utilisant la taille du mini-paquet de 10, la vitesse d'apprentissage η = 0,5, le paramètre de régularisation λ = 5,0 et la fonction de coût avec entropie croisée. Nous formerons un réseau de 30 époques à l'aide d'un ensemble complet de données, et augmenterons le nombre d'époques proportionnellement à la diminution du volume des données de formation. Pour garantir le même facteur de réduction de poids pour différents ensembles de données d'entraînement, nous utiliserons le paramètre de régularisation λ = 5,0 avec un ensemble de formation complet, et réduisez-le proportionnellement avec une diminution des volumes de données.


Exercice
- Comme nous l'avons vu ci-dessus, une façon d'étendre les données d'entraînement du MNIST consiste à utiliser de petites rotations des images d'entraînement. Quel problème peut apparaître si nous autorisons la rotation des images sous tous les angles?
Digression des mégadonnées et signification de la comparaison de l'exactitude de la classification
Examinons à nouveau comment la précision de notre NS varie en fonction de la taille de l'ensemble de formation:Supposons qu'au lieu d'utiliser NS, nous utiliserions une autre technologie d'apprentissage automatique pour classer les nombres. Par exemple, essayons d'utiliser la méthode de support vector machine (SVM), que nous avons brièvement rencontrée au chapitre 1. Comme alors, ne vous inquiétez pas si vous n'êtes pas familier avec SVM, nous n'avons pas besoin de comprendre ses détails. Nous utiliserons SVM via la bibliothèque scikit-learn. Voici comment l'efficacité de SVM varie en fonction de la taille de l'ensemble d'entraînement. A titre de comparaison, j'ai mis le calendrier et les résultats de l'Assemblée nationale.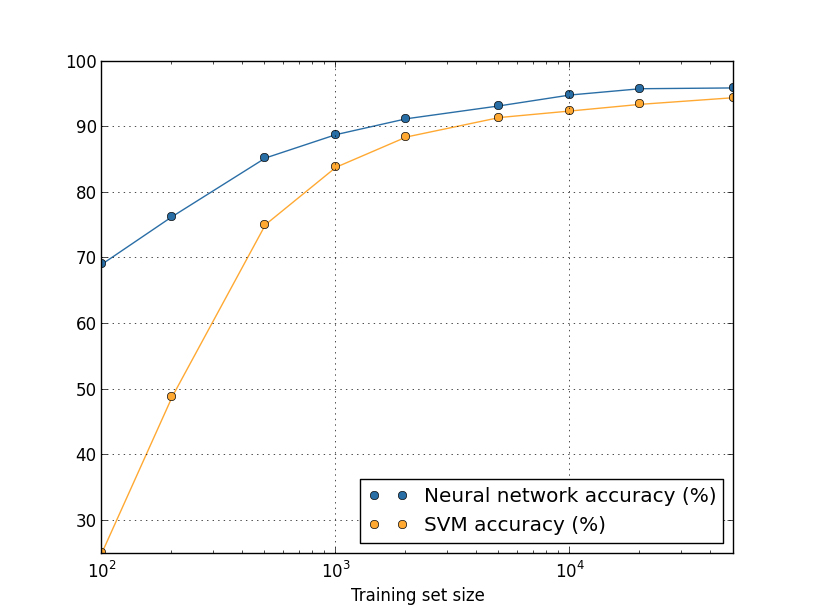
Défi
- . ? . – , , , . , . - ? , .
Résumé
Nous avons terminé notre immersion en recyclage et régularisation. Bien sûr, nous reviendrons sur ces problèmes. Comme je l'ai déjà mentionné à plusieurs reprises, le recyclage est un gros problème dans le domaine de la NS, d'autant plus que les ordinateurs deviennent plus puissants et que nous pouvons former des réseaux plus importants. En conséquence, il est urgent de développer des techniques de régularisation efficaces pour réduire le recyclage, ce domaine est donc très actif aujourd'hui.
Initialisation du poids
Lorsque nous créons notre NS, nous devons choisir les valeurs initiales des poids et des décalages. Jusqu'à présent, nous les avons choisis selon les directives brièvement décrites au chapitre 1. Permettez-moi de vous rappeler que nous avons choisi des poids et des décalages basés sur une distribution gaussienne indépendante avec une attente mathématique de 0 et un écart-type de 1. Cette approche a bien fonctionné, mais elle semble plutôt arbitraire, donc ça vaut le coup révisez-le et pensez s'il est possible de trouver une meilleure façon d'affecter les poids et déplacements initiaux et, peut-être, d'aider nos NS à apprendre plus rapidement.
Il s'avère que le processus d'initialisation peut être sérieusement amélioré par rapport à la distribution gaussienne normalisée. Pour comprendre cela, disons que nous travaillons avec un réseau avec un grand nombre de neurones d'entrée, disons, de 1000. Et disons que nous avons utilisé la distribution gaussienne normalisée pour initialiser les poids connectés à la première couche cachée. Jusqu'à présent, je vais me concentrer uniquement sur les échelles reliant les neurones d'entrée au premier neurone de la couche cachée, et ignorer le reste du réseau:
Pour simplifier, imaginons que nous essayons de former le réseau avec l'entrée x, dans laquelle la moitié des neurones d'entrée sont activés, c'est-à-dire qu'ils ont une valeur de 1, et la moitié sont désactivés, c'est-à-dire qu'ils ont une valeur de 0. L'argument suivant fonctionne dans un cas plus général, mais c'est plus facile pour vous le comprendra sur cet exemple particulier. Considérons la somme pondérée z = ∑
j w
j x
j + b des entrées pour un neurone caché. 500 membres de la somme disparaissent parce que les x
j correspondants sont 0. Par conséquent, z est la somme de 501 variables aléatoires gaussiennes normalisées, 500 poids et 1 décalage supplémentaire. Par conséquent, la valeur z elle-même a une distribution gaussienne avec une espérance mathématique de 0 et un écart-type de √501 ≈ 22,4. Autrement dit, z a une distribution gaussienne assez large, sans pics nets:

En particulier, ce graphique montre que | z | est susceptible d'être assez grand, c'est-à-dire z ≫ 1 ou z ≫ -1. Dans ce cas, la sortie des neurones cachés σ (z) sera très proche de 1 ou 0. Cela signifie que notre neurone caché sera saturé. Et lorsque cela se produit, comme nous le savons déjà, de petits changements de poids produiront de minuscules changements dans l'activation d'un neurone caché. Ces petits changements, à leur tour, n'affecteront pratiquement pas les neutrons restants dans le réseau, et nous verrons les petits changements correspondants dans la fonction de coût. Par conséquent, ces poids seront entraînés très lentement lorsque nous utiliserons l'algorithme de descente de gradient. Ceci est similaire à la tâche que nous avons déjà discutée dans ce chapitre, dans laquelle les neurones de sortie saturés de valeurs incorrectes ralentissent l'apprentissage. Nous avions l'habitude de résoudre ce problème en choisissant intelligemment une fonction de coût. Malheureusement, bien que cela ait aidé avec les neurones de sortie saturés, cela n'aide pas du tout avec la saturation des neurones cachés.
Maintenant, j'ai parlé des échelles entrantes de la première couche cachée. Naturellement, les mêmes arguments s'appliquent aux couches cachées suivantes: si les poids des couches cachées ultérieures sont initialisés à l'aide de distributions gaussiennes normalisées, leur activation sera souvent proche de 0 ou 1, et la formation se déroulera très lentement.
Existe-t-il un moyen de choisir les meilleures options d'initialisation pour les pondérations et les décalages, afin de ne pas obtenir une telle saturation et d'éviter les retards d'apprentissage? Supposons que nous ayons un neurone avec le nombre de poids entrants n po. Ensuite, nous devons initialiser ces poids avec des distributions gaussiennes aléatoires avec une espérance mathématique de 0 et un écart-type de 1 / √n
in . Autrement dit, nous compressons les gaussiens et réduisons la probabilité de saturation du neurone. Ensuite, nous choisissons une distribution gaussienne pour les déplacements avec une espérance mathématique de 0 et un écart-type de 1, pour des raisons que je reviendrai un peu plus loin. Après avoir fait ce choix, nous constatons à nouveau que z = ∑
j w
j x
j + b sera une variable aléatoire avec une distribution gaussienne avec une attente mathématique de 0, mais avec un pic beaucoup plus prononcé qu'auparavant. Supposons, comme précédemment, que 500 entrées soient 0 et 500 sont 1. Ensuite, il est facile de montrer (voir l'exercice ci-dessous) que z a une distribution gaussienne avec une espérance mathématique de 0 et un écart-type de √ (3/2) = 1,22 ... Ce graphique a un pic beaucoup plus net, à tel point que même dans l'image ci-dessous, la situation est quelque peu sous-estimée, car j'ai dû changer l'échelle de l'axe vertical par rapport au graphique précédent:
Un tel neurone sera saturé avec une probabilité beaucoup plus faible et, par conséquent, il sera moins susceptible de rencontrer un ralentissement de l'apprentissage.
Exercice
- Confirmer que l'écart type de z = ∑ j w j x j + b par rapport au paragraphe précédent est √ (3/2). Considérations en faveur de ceci: la variance de la somme des variables aléatoires indépendantes est égale à la somme des variances des variables aléatoires individuelles; la variance est égale au carré de l'écart type.
J'ai mentionné ci-dessus que nous continuerons à initialiser les déplacements, comme précédemment, sur la base d'une distribution gaussienne indépendante avec une attente mathématique de 0 et un écart-type de 1. Et c'est normal, car cela n'augmente pas considérablement la probabilité de saturation de nos neurones. En fait, l'initialisation des décalages n'a pas beaucoup d'importance si nous parvenons à éviter le problème de saturation. Certains tentent même d'initialiser tous les décalages à zéro et s'appuient sur le fait que la descente en gradient peut apprendre les décalages appropriés. Mais comme la probabilité que cela affecte quelque chose est faible, nous continuerons à utiliser la même procédure d'initialisation qu'auparavant.
Comparons les résultats des anciennes et des nouvelles approches pour initialiser les poids en utilisant la tâche de classer les nombres du MNIST. Comme précédemment, nous utiliserons 30 neurones cachés, un mini-paquet de taille 10, un paramètre de régularisation & lambda = 5,0, et une fonction de coût avec entropie croisée. Nous réduirons progressivement la vitesse d'apprentissage de η = 0,5 à 0,1, car de cette façon les résultats seront légèrement mieux visibles sur les graphiques. Vous pouvez apprendre en utilisant l'ancienne méthode d'initialisation du poids:
>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True)
Vous pouvez également apprendre à utiliser la nouvelle approche pour initialiser les poids. C'est encore plus simple, car par défaut, network2 initialise les poids en utilisant une nouvelle approche. Cela signifie que nous pouvons omettre l'appel net.large_weight_initializer () plus tôt:
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True)
On trace (en utilisant le programme weight_initialization.py):
Dans les deux cas, une précision de classement de 96% est obtenue. La précision résultante est presque la même dans les deux cas. Mais la nouvelle technique d'initialisation atteint ce point beaucoup, beaucoup plus rapidement. À la fin de la dernière ère de formation, l'ancienne approche d'initialisation des poids atteint une précision de 87% et la nouvelle approche approche déjà 93%. Apparemment, une nouvelle approche pour initialiser les poids part d'une position bien meilleure, donc nous obtenons de bons résultats beaucoup plus rapidement. Le même phénomène s'observe si l'on construit les résultats d'un réseau de 100 neurones:
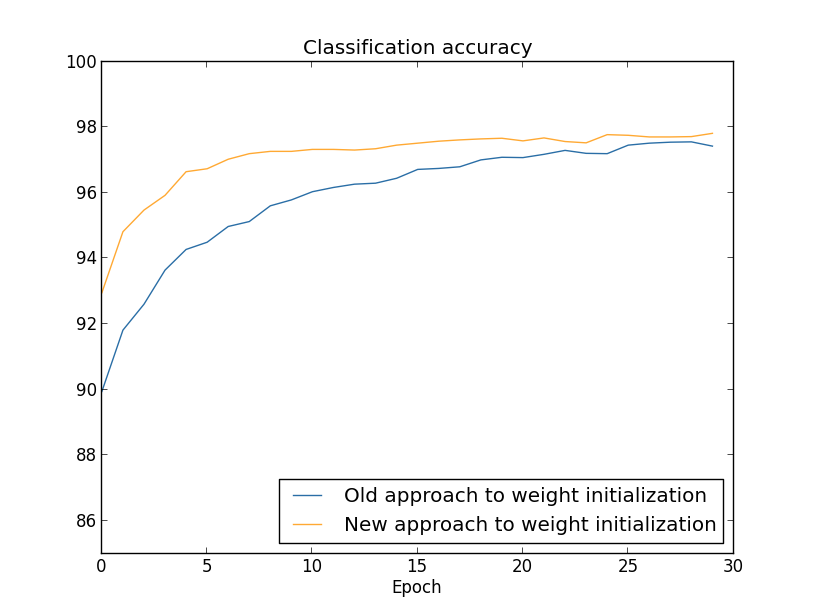
Dans ce cas, deux courbes ne se produisent pas. Cependant, mes expériences disent que si vous ajoutez un peu plus d'époques, la précision commence à presque coïncider. Par conséquent, sur la base de ces expériences, nous pouvons dire que l'amélioration de l'initialisation des poids ne fait qu'accélérer la formation, mais ne modifie pas l'efficacité globale du réseau. Cependant, au chapitre 4, nous verrons des exemples de NS dans lesquels l'efficacité à long terme est considérablement améliorée en raison de l'initialisation des pondérations à 1 / √n
in . Par conséquent, il améliore non seulement la vitesse d'apprentissage, mais parfois l'efficacité qui en résulte.
L'approche de l'initialisation des poids via 1 / √n
in permet d'améliorer la formation des réseaux de neurones. D'autres techniques d'initialisation des poids ont été proposées, dont beaucoup sont basées sur cette idée de base. Je ne les considérerai pas ici, car 1 / √n
in fonctionne bien pour nos besoins. Si vous êtes intéressé, je vous recommande de lire la discussion des pages 14 et 15 dans un
article de 2012 de Yoshua Benggio.
Défi
- La combinaison de la régularisation et d'une méthode d'initialisation de poids améliorée. Parfois, la régularisation de L2 nous donne automatiquement des résultats similaires à une nouvelle méthode d'initialisation des poids. Disons que nous utilisons l'ancienne approche pour initialiser les poids. Esquissez un argument heuristique prouvant que: (1) si λ n'est pas trop petit, alors dans les premières époques d'entraînement, l'affaiblissement des poids dominera presque complètement; (2) si ηλ ≪ n, alors les poids affaibliront e −ηλ / m fois à l'époque; (3) si λ n'est pas trop grand, l'affaiblissement des poids ralentit lorsque les poids diminuent à environ 1 / √n, où n est le nombre total de poids dans le réseau. Démontrer que ces conditions sont remplies dans les exemples pour lesquels les graphiques sont construits dans cette section.
Retour à la reconnaissance de l'écriture manuscrite: code
Implémentons les idées décrites dans ce chapitre. Nous allons développer un nouveau programme, network2.py, une version améliorée du programme network.py que nous avons créé au chapitre 1. Si vous n'avez pas vu son code depuis longtemps, il peut être utile de le parcourir rapidement. Ce ne sont que 74 lignes de code, et c'est facile à comprendre.
Comme avec network.py, l'étoile de network2.py est la classe Network, que nous utilisons pour représenter nos NS. Nous initialisons l'instance de classe avec une liste de tailles des couches réseau correspondantes, et avec le choix de la fonction de coût, par défaut ce sera l'entropie croisée:
class Network(object): def __init__(self, sizes, cost=CrossEntropyCost): self.num_layers = len(sizes) self.sizes = sizes self.default_weight_initializer() self.cost=cost
Les deux premières lignes de la méthode __init__ sont les mêmes que network.py et sont comprises par elles-mêmes. Les deux lignes suivantes sont nouvelles et nous devons comprendre en détail ce qu'elles font.
Commençons par la méthode default_weight_initializer. Il utilise une nouvelle approche améliorée pour initialiser les poids. Comme nous l'avons vu, dans cette approche, les poids entrant dans le neurone sont initialisés sur la base d'une distribution gaussienne indépendante avec une attente mathématique de 0 et un écart-type de 1 divisé par la racine carrée du nombre de liens entrants vers le neurone. De plus, cette méthode initialisera les décalages en utilisant la distribution gaussienne avec une moyenne de 0 et un écart-type de 1. Voici le code:
def default_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]
Pour le comprendre, vous devez vous rappeler que np est une bibliothèque Numpy traitant de l'algèbre linéaire. Nous l'avons importé au début du programme. Notez également que nous n'initialisons pas les déplacements dans la première couche de neurones. La première couche est entrante, les décalages ne sont donc pas utilisés. Le même était network.py.
En plus de la méthode default_weight_initializer, nous allons créer une méthode large_weight_initializer. Il initialise les pondérations et les décalages en utilisant l'ancienne approche du chapitre 1, où les pondérations et les compensations sont initialisées sur la base d'une distribution gaussienne indépendante avec une attente mathématique de 0 et un écart-type de 1. Ce code, bien sûr, n'est pas très différent de default_weight_initializer:
def large_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]
J'ai inclus cette méthode principalement parce qu'il était plus pratique pour nous de comparer les résultats de ce chapitre et du chapitre 1. Je ne peux imaginer de réelles options dans lesquelles je recommanderais de l'utiliser!
La deuxième nouveauté de la méthode __init__ sera l'initialisation de l'attribut cost. Pour comprendre comment cela fonctionne, regardons la classe que nous utilisons pour représenter la fonction de coût d'entropie croisée (la directive @staticmethod indique à l'interpréteur que cette méthode est indépendante de l'objet, donc le paramètre self n'est pas transmis aux méthodes fn et delta).
class CrossEntropyCost(object): @staticmethod def fn(a, y): return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a))) @staticmethod def delta(z, a, y): return (ay)
Voyons cela. La première chose que l'on peut voir ici est que, bien que l'entropie croisée soit une fonction d'un point de vue mathématique, nous l'implémentons en tant que classe python, pas en tant que fonction python. Pourquoi ai-je décidé de faire ça? Dans notre réseau, la valeur joue deux rôles différents. Évident - c'est une mesure de la mesure dans laquelle l'activation de la sortie a correspond à la sortie souhaitée y. Ce rôle est fourni par la méthode CrossEntropyCost.fn. (Soit dit en passant, notez que l'appel de np.nan_to_num dans CrossEntropyCost.fn garantit que Numpy traite correctement le logarithme des nombres proches de zéro). Cependant, la fonction de coût est utilisée dans notre réseau de la deuxième manière. Nous rappelons du chapitre 2 que lors du démarrage de l'algorithme de rétropropagation, nous devons considérer l'erreur de sortie du réseau δ
L. La forme de l'erreur de sortie dépend de la fonction de coût: différentes fonctions de coût auront différentes formes d'erreur de sortie. Pour l'entropie croisée, l'erreur de sortie, comme suit de l'équation (66), sera égale à:
Par conséquent, je définis une deuxième méthode, CrossEntropyCost.delta, dont le but est d'expliquer au réseau comment calculer l'erreur de sortie. Et puis nous combinons ces deux méthodes en une seule classe contenant tout ce que notre réseau doit savoir sur la fonction de coût.
Pour une raison similaire, network2.py contient une classe qui représente une fonction de coût quadratique. Y compris pour comparaison avec les résultats du chapitre 1, car à l'avenir, nous utiliserons principalement l'entropie croisée. Le code est ci-dessous. La méthode QuadraticCost.fn est un calcul simple du coût quadratique associé à la sortie a et à la sortie souhaitée y. La valeur renvoyée par QuadraticCost.delta est basée sur l'expression (30) de l'erreur de sortie de la valeur quadratique, que nous avons dérivée au chapitre 2.
class QuadraticCost(object): @staticmethod def fn(a, y): return 0.5*np.linalg.norm(ay)**2 @staticmethod def delta(z, a, y): return (ay) * sigmoid_prime(z)
Nous avons maintenant compris les principales différences entre network2.py et network2.py. Tout est très simple. Il y a d'autres petits changements que je décrirai ci-dessous, notamment la mise en place de la régularisation de L2. Avant cela, regardons le code network2.py complet. Il n'est pas nécessaire de l'étudier en détail, mais il vaut la peine de comprendre la structure de base, en particulier, de lire les commentaires pour comprendre ce que fait chacun des éléments du programme. Bien sûr, je n'interdit pas de vous plonger dans cette question autant que vous le souhaitez! Si vous vous perdez, essayez de lire le texte après le programme et revenez au code. En général, c'est ici:
"""network2.py ~~~~~~~~~~~~~~ network.py, . – , , . , . , . """
Parmi les changements les plus intéressants figure l'inclusion de la régularisation L2. Bien qu'il s'agisse d'un grand changement conceptuel, il est si facile à implémenter que vous ne le remarquerez peut-être pas dans le code. Pour la plupart, cela passe simplement le paramètre lmbda à différentes méthodes, en particulier Network.SGD. Tout le travail est effectué sur une ligne du programme, la quatrième à partir de la fin dans la méthode Network.update_mini_batch. Là, nous changeons la règle de mise à jour de la descente de gradient pour inclure la réduction de poids. Le changement est minime, mais affecte sérieusement les résultats!
Soit dit en passant, cela se produit souvent lors de la mise en œuvre de nouvelles techniques dans les réseaux de neurones. Nous avons passé des milliers de mots à discuter de la régularisation. Conceptuellement, c'est une chose assez subtile et difficile à comprendre. Cependant, il peut être trivialement ajouté au programme! De façon inattendue, des techniques complexes peuvent être mises en œuvre avec des modifications mineures de code.
Un autre changement petit mais important dans le code est l'ajout de plusieurs indicateurs optionnels à la méthode de descente de gradient stochastique Network.SGD.
Ces drapeaux permettent de suivre les coûts et la précision sur training_data ou evaluation_data, qui peuvent être transmis à Network.SGD. Plus tôt dans le chapitre, nous avons souvent utilisé ces indicateurs, mais permettez-moi de donner un exemple de leur utilisation, juste pour rappel: >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.SGD(training_data, 30, 10, 0.5, ... lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True, ... monitor_evaluation_cost=True, ... monitor_training_accuracy=True, ... monitor_training_cost=True)
Nous définissons evaluation_data via validation_data. Cependant, nous pourrions suivre les performances sur test_data et tout autre ensemble de données. Nous avons également quatre indicateurs qui spécifient la nécessité de suivre les coûts et la précision à la fois sur evaluation_data et training_data. Ces indicateurs sont définis sur False par défaut, mais ils sont inclus ici pour suivre l'efficacité du réseau. De plus, la méthode Network.SGD de network2.py renvoie un tuple à quatre éléments représentant les résultats du suivi. Vous pouvez l'utiliser comme ceci: >>> evaluation_cost, evaluation_accuracy, ... training_cost, training_accuracy = net.SGD(training_data, 30, 10, 0.5, ... lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True, ... monitor_evaluation_cost=True, ... monitor_training_accuracy=True, ... monitor_training_cost=True)
Ainsi, par exemple, evaluation_cost sera une liste de 30 éléments contenant le coût des données estimées à la fin de chaque ère. Ces informations sont extrêmement utiles pour comprendre le comportement d'un réseau neuronal. Ces informations sont extrêmement utiles pour comprendre le comportement du réseau. Il peut, par exemple, être utilisé pour tracer des graphiques de l'apprentissage réseau au fil du temps. C'est ainsi que j'ai construit tous les graphiques de ce chapitre. Cependant, si l'un des indicateurs n'est pas défini, l'élément de tuple correspondant sera une liste vide.D'autres ajouts de code incluent la méthode Network.save, qui enregistre l'objet Network sur le disque, et la fonction de le charger en mémoire. L'enregistrement et le chargement se font via JSON, pas les modules Python pickle ou cPickle, qui sont généralement utilisés pour enregistrer sur le disque et charger en python. L'utilisation de JSON nécessite plus de code que ce qui serait nécessaire pour pickle ou cPickle. Pour comprendre pourquoi j'ai choisi JSON, imaginez qu'à un moment donné dans le futur, nous avons décidé de changer notre classe de réseau afin qu'il y ait plus que des neurones sigmoïdes. Pour implémenter ce changement, nous changerions très probablement les attributs définis dans la méthode Network .__ init__. Et si nous utilisions juste du cornichon pour économiser, notre fonction de chargement ne fonctionnerait pas. L'utilisation de JSON avec une sérialisation explicite nous permet de garantir facilementque les anciennes versions de l'objet Réseau peuvent être téléchargées.Il y a beaucoup de petits changements dans le code, mais ce ne sont que de petites variations de network.py. Le résultat final est une extension de notre programme de 74 lignes à un programme beaucoup plus fonctionnel de 152 lignes.Défi
- Modifiez le code ci-dessous en introduisant la régularisation L1, et utilisez-le pour classer les chiffres MNIST par un réseau avec 30 neurones cachés. Pouvez-vous choisir un paramètre de régularisation qui vous permet d'améliorer le résultat par rapport à un réseau sans régularisation?
- Network.cost_derivative method network.py. . ? , ? network2.py Network.cost_derivative, CrossEntropyCost.delta. ?