Aujourd'hui, nous allons examiner un package graphique pour la langue Julia appelé Luxor . C'est l'un de ces outils qui transforme le processus de création d'images vectorielles en résolution de problèmes logiques avec une tempête d'émotions qui l'accompagne.
Attention Sous la coupe, 8,5 Mo d'images et de gifs légers représentant des œufs psychédéliques et des objets à quatre dimensions, dont la visualisation peut provoquer une légère opacification de l'esprit!
L'installation
https://julialang.org - téléchargez la distribution Julia sur le site officiel. Ensuite, en démarrant l'interpréteur, nous lançons les commandes dans sa console:
using Pkg Pkg.add("Colors") Pkg.add("ColorSchemes") Pkg.add("Luxor")
qui installera des packages pour un travail avancé avec les couleurs et Luxor lui-même.
Problèmes possibles
Le principal problème de la programmation moderne en général et de l'open source en particulier est que certains projets sont construits les uns sur les autres, héritant de toutes les erreurs, ou même en générant de nouvelles en raison d'incompatibilités. Comme de nombreux autres packages, Luxor utilise d'autres packages julia pour son travail, qui, à leur tour, sont des coquilles de solutions existantes.
Donc, ImageMagick.jl ne voulait pas télécharger et enregistrer des fichiers. La solution a été trouvée sur la page d' origine - il s'est avéré qu'il n'aime pas l'alphabet cyrillique à certains égards.
Le problème numéro deux est survenu avec le package graphique de bas niveau du Caire sous Windows 7. Je vais cacher la solution ici:
Danser avec un tambourin- Nous tapons l'interpréteur
]add Gtk - le paquet pour travailler avec gui commencera à être installé et très probablement il tombera pendant la construction - Ensuite, téléchargez gtk + -bundle_3.6.4-20130513_win64
- Pendant l'installation, tout était nécessaire dans le dossier contenant les packages de Julia, mais gtk n'était pas terminé pendant l'exécution de l'élément, nous avons donc téléchargé la version finale pour notre machine - nous jetons le contenu de l'archive téléchargée dans le répertoire C: \ Users \ User.julia \ packages \ WinRPM \ Y9QdZ \ deps \ usr \ x86_64-w64-mingw32 \ sys-root \ mingw (votre chemin peut varier)
- Exécutez julia et conduisez
]build Gtk et après avoir construit en using Gtk , et, par souci de fidélité, reconstruisez Louxor: ]build Luxor - Nous redémarrons Julia et nous pouvons utiliser en toute sécurité tout ce dont nous avons besoin:
using Luxor
En cas d'autres problèmes, nous essayons de trouver notre cas
Si vous voulez essayer l'animation
Le package Luxor crée des animations à l'aide de ffmpeg , à condition qu'il soit présent sur votre ordinateur. ffmpeg est une bibliothèque open source multiplateforme pour le traitement de fichiers vidéo et audio, une chose très utile (il y a une bonne excursion sur le hub ). Installez-le:
- Téléchargez ffmpeg hors site. Dans mon cas, c'est un téléchargement pour Windows
- Décompressez et écrivez le chemin d'accès à ffmpeg.exe dans la variable Path .
En savoir plus sur le colmatage dans Path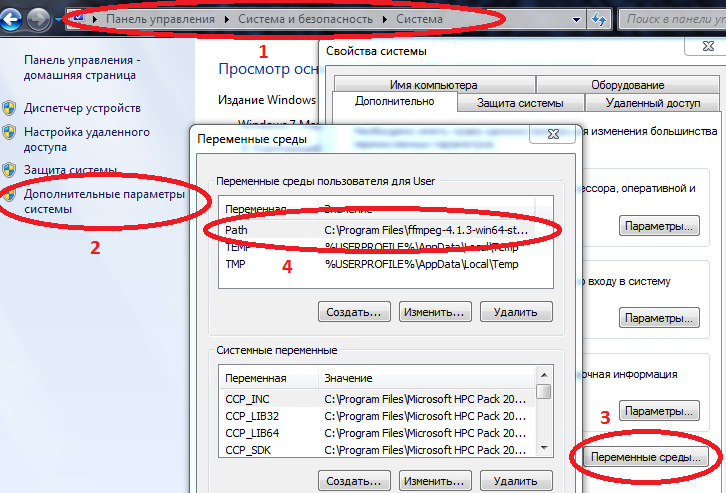
Ordinateur / Propriétés système / Paramètres système avancés / Variables d'environnement / Chemin d'accès (Créer sinon) et ajoutez-y le chemin d'accès à votre ffmpeg.exe
Exemple C: \ Program Files \ ffmpeg-4.1.3-win64-static \ bin
si Path a déjà des valeurs, séparez-les par un point-virgule.
Maintenant, si vous conduisez ffmpeg avec les paramètres nécessaires dans la console de commande ( cmd ), il démarrera et fonctionnera et Julia ne communiquera qu'avec lui.
Bonjour tout le monde
Commençons par un petit piège - lors de la construction d'une image, un fichier graphique est créé et enregistré dans le répertoire de travail. Autrement dit, lorsque vous travaillez dans REPL, le dossier racine julia sera obstrué d'images, et si vous dessinez dans Jupyter, alors les images s'accumulent à côté du cahier de projet, par conséquent, ce sera une bonne habitude de définir le répertoire de travail dans un endroit séparé avant de commencer le travail:
using Luxor cd("C:\\Users\\User\\Desktop\\mycop")
Créez le premier dessin
Drawing(220, 220, "hw.png") origin() background("white") sethue("black") text("Hello world") circle(Point(0, 0), 100, :stroke) finish() preview()

Drawing() crée un dessin, par défaut au format PNG, le nom de fichier par défaut est 'luxor-drawing.png', la taille par défaut est 800x800, pour tous les formats sauf png, vous pouvez spécifier des tailles non entières, et vous pouvez également utiliser des tailles de feuille de papier ("A0 "," A1 "," A2 "," A3 "," A4 "...)
finish() - termine le dessin et ferme le fichier. Vous pouvez l'ouvrir dans une application de visualisation externe en utilisant preview() , qui lorsque vous travaillez dans Jupyter (IJulia) affichera un fichier PNG ou SVG dans le bloc-notes. Lorsque vous travaillez dans Juno, il affichera un fichier PNG ou SVG dans le panneau Graphique. Dans Repl, l'outil pour travailler avec des images que vous définissez pour ce format dans votre système d'exploitation est appelé.
La même chose peut être écrite sous forme abrégée à l'aide de macros
@png begin text("Hello world") circle(Point(0, 0), 100, :stroke) end
Pour les formats vectoriels EPS, SVG, PDF, tout fonctionne de la même manière.
Oeuf euclidien

C'est une façon plutôt intéressante de dessiner un œuf, et si vous connectez les points clés et coupez le long des lignes reçues, un excellent tangram sortira
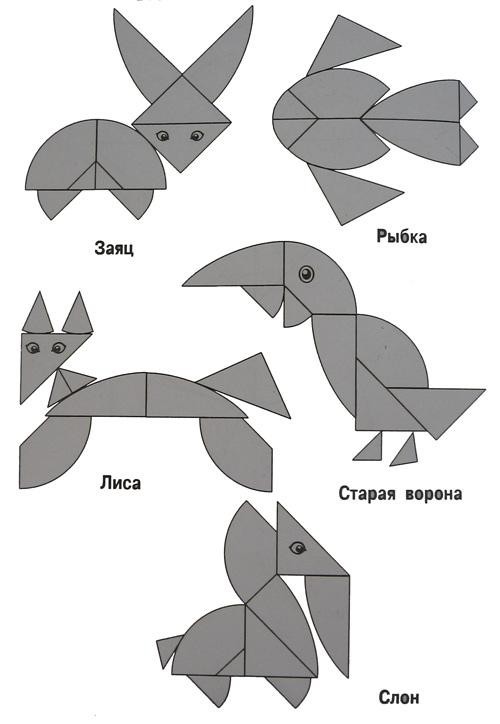
Commençons par le cercle:
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) end 200 200 "egg0"

Tout est extrêmement simple: setdash("dot") - dessiner avec des points, sethue("gray30") - couleur de la ligne: plus le plus petit, le plus sombre, le plus proche de 100 le plus blanc. La classe de points est définie sans nous et le centre des coordonnées (0,0) peut être spécifié par la lettre O Ajoutez deux cercles et signez les points:
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke) end 600 400 "egg2"
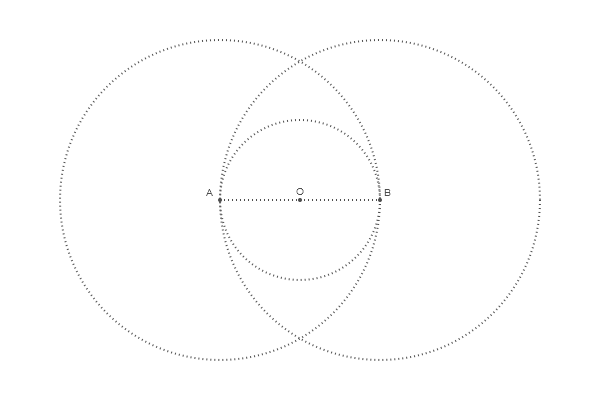
Pour rechercher des points d'intersection, il existe une fonction appelée intersectionlinecircle() qui trouve le ou les points où la ligne coupe le cercle. Ainsi, nous pouvons trouver deux points où l'un des cercles coupe une ligne verticale imaginaire tracée à travers O. En raison de la symétrie, nous ne pouvons traiter que le cercle A.
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)
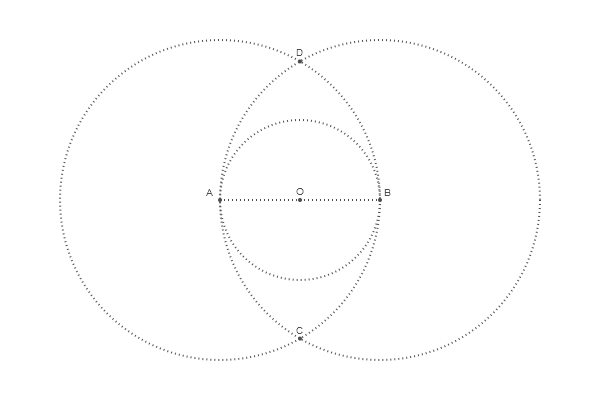
Pour déterminer le centre du cercle supérieur, nous trouvons l'intersection OD
Code @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)

Le rayon du cercle subordonné est déterminé par la restriction à deux grands cercles:
Code @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)

L'œuf est prêt! Il reste à l'assembler à partir de quatre arcs spécifiés par la fonction arc2r() et à remplir la zone:
Code @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)
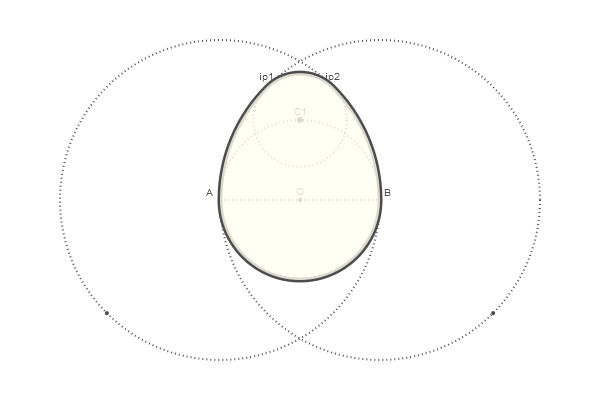
Et maintenant, afin de se livrer correctement, nous allons apporter nos réalisations à
la fonction function egg(radius, action=:none) A, B = [Point(x, 0) for x in [-radius, radius]] nints, C, D = intersectionlinecircle(Point(0, -2radius), Point(0, 2radius), A, 2radius) flag, C1 = intersectionlinecircle(C, D, O, radius) nints, I3, I4 = intersectionlinecircle(A, C1, A, 2radius) nints, I1, I2 = intersectionlinecircle(B, C1, B, 2radius) if distance(C1, I1) < distance(C1, I2) ip1 = I1 else ip1 = I2 end if distance(C1, I3) < distance(C1, I4) ip2 = I3 else ip2 = I4 end newpath() arc2r(B, A, ip1, :path) arc2r(C1, ip1, ip2, :path) arc2r(A, ip2, B, :path) arc2r(O, B, A, :path) closepath() do_action(action) end
Nous utilisons des couleurs aléatoires, des couches de peinture et diverses conditions initiales:
@png begin setopacity(0.7) for θ in range(0, step=π/6, length=12) @layer begin rotate(θ) translate(100, 50)


En plus du contour et du remplissage, vous pouvez utiliser le contour comme zone de découpe (recadrer une autre image sous la forme d'un œuf) ou comme base pour divers concepteurs. La fonction egg () crée un contour et vous permet de lui appliquer une action. Il est également possible de transformer notre création en un polygone (un tableau de points). Le code suivant convertit le contour d'un œuf en polygone, puis déplace chaque point du polygone à mi-chemin vers le centre de gravité.
@png begin egg(160, :path) pgon = first(pathtopoly()) pc = polycentroid(pgon) circle(pc, 5, :fill) for pt in 1:2:length(pgon) pgon[pt] = between(pc, pgon[pt], 0.5) end poly(pgon, :stroke) end 350 500 "polyegg"

L'apparence inégale des points internes apparaît ici en raison des paramètres de connexion de ligne par défaut. Expérimentez avec setlinejoin("round") pour voir si cela change la géométrie. Eh bien, essayons maintenant offsetpoly() créer un contour polygonal à l'extérieur ou à l'intérieur d'un polygone existant.
@png begin egg(80, :path) pgon = first(pathtopoly()) pc = polycentroid(pgon) for pt in 1:2:length(pgon) pgon[pt] = between(pc, pgon[pt], 0.9) end for i in 30:-3:-8 randomhue() op = offsetpoly(pgon, i) poly(op, :stroke, close=true) end end 350 500 "polyeggs"

De petits changements dans la régularité des points créés en convertissant le chemin en un polygone, et le nombre différent d'échantillons qu'il a fait, sont constamment amplifiés en contours successifs.
L'animation
Tout d'abord, définissons les fonctions qui implémentent l'arrière-plan et le rendu de l'oeuf, en fonction du numéro de trame:
Code using Colors demo = Movie(400, 400, "test") function backdrop(scene, framenumber) background("black") end function frame(scene, framenumber) setopacity(0.7) θ = framenumber * π/6 @layer begin rotate(θ) translate(100, 50) egg(50, :path) setline(10) randomhue() fillpreserve() randomhue() strokepath() end end
L'animation est implémentée par un simple ensemble de commandes:
animate(demo, [ Scene(demo, backdrop, 0:12), Scene(demo, frame, 0:12, easingfunction=easeinoutcubic, optarg="made with Julia") ], framerate=10, tempdirectory="C:\\Users\\User\\Desktop\\mycop", creategif=true)
Ce qui cause réellement notre ffmpeg
run(`ffmpeg -f image2 -i $(tempdirectory)/%10d.png -vf palettegen -y $(seq.stitle)-palette.png`) run(`ffmpeg -framerate 30 -f image2 -i $(tempdirectory)/%10d.png -i $(seq.stitle)-palette.png -lavfi paletteuse -y /tmp/$(seq.stitle).gif`)
Autrement dit, une série d'images est créée, puis un GIF est assemblé à partir de ces cadres:

Pentahore
Il est un cinq - noyau - le simplexe à quatre dimensions correct. Pour dessiner et manipuler des objets à 4 dimensions sur des images à deux dimensions, nous définissons d'abord
point de classe 4 dimensions struct Point4D <: AbstractArray{Float64, 1} x::Float64 y::Float64 z::Float64 w::Float64 end Point4D(a::Array{Float64, 1}) = Point4D(a...) Base.size(pt::Point4D) = (4, ) Base.getindex(pt::Point4D, i) = [pt.x, pt.y, pt.z, pt.w][i] struct Point3D <: AbstractArray{Float64, 1} x::Float64 y::Float64 z::Float64 end Base.size(pt::Point3D) = (3, )
Au lieu de définir de nombreuses opérations manuellement, nous pouvons définir notre structure comme un sous-type de AbstractArray (En savoir plus sur les classes en tant qu'interfaces )
La tâche principale que nous devons résoudre est de savoir comment convertir un point 4D en un point 2D. Commençons par une tâche plus simple: comment convertir un point 3D en un point 2D, c'est-à-dire Comment dessiner une figure 3D sur une surface plane? Prenons un simple cube. Les surfaces avant et arrière peuvent avoir les mêmes coordonnées X et Y et ne varient que dans leurs valeurs Z.
Code @png begin fontface("Menlo") fontsize(8) setblend(blend( boxtopcenter(BoundingBox()), boxmiddlecenter(BoundingBox()), "skyblue", "white")) box(boxtopleft(BoundingBox()), boxmiddleright(BoundingBox()), :fill) setblend(blend( boxmiddlecenter(BoundingBox()), boxbottomcenter(BoundingBox()), "grey95", "grey45" )) box(boxmiddleleft(BoundingBox()), boxbottomright(BoundingBox()), :fill) sethue("black") setline(2) bx1 = box(O, 250, 250, vertices=true) poly(bx1, :stroke, close=true) label.(["-1 1 1", "-1 -1 1", "1 -1 1", "1 1 1"], slope.(O, bx1), bx1) setline(1) bx2 = box(O, 150, 150, vertices=true) poly(bx2, :stroke, close=true) label.(["-1 1 0", "-1 -1 0", "1 -1 0", "1 1 0"], slope.(O, bx2), bx2, offset=-45) map((x, y) -> line(x, y, :stroke), bx1, bx2) end 400 400 "cube.png"

Par conséquent, l'idée est de projeter un cube de 3D en 2D, en enregistrant les deux premières valeurs et en les multipliant ou en les modifiant par la troisième valeur. Vérifier
comment ça marche const K = 4.0 function convert(Point, pt3::Point3D) k = 1/(K - pt3.z) return Point(pt3.x * k, pt3.y * k) end @png begin cube = Point3D[ Point3D(-1, -1, 1), Point3D(-1, 1, 1), Point3D( 1, -1, 1), Point3D( 1, 1, 1), Point3D(-1, -1, -1), Point3D(-1, 1, -1), Point3D( 1, -1, -1), Point3D( 1, 1, -1), ] circle.(convert.(Point, cube) * 300, 5, :fill) end 220 220 "points"

En utilisant le même principe, créons une méthode de conversion des points 4D et une fonction qui prend une liste de points à quatre dimensions et les mappe deux fois à une liste de points à deux dimensions convenant au dessin.
function convert(Point3D, pt4::Point4D) k = 1/(K - pt4.w) return Point3D(pt4.x * k, pt4.y * k, pt4.z * k) end function flatten(shape4) return map(pt3 -> convert(Point, pt3), map(pt4 -> convert(Point3D, pt4), shape4)) end
Ensuite, définissez les sommets et les faces et vérifiez comment cela fonctionne en couleur
Tyk! const n = -1/√5 const pentachoron = [Point4D(vertex...) for vertex in [ [ 1.0, 1.0, 1.0, n], [ 1.0, -1.0, -1.0, n], [-1.0, 1.0, -1.0, n], [-1.0, -1.0, 1.0, n], [ 0.0, 0.0, 0.0, n + √5]]]; const pentachoronfaces = [ [1, 2, 3], [1, 2, 4], [1, 2, 5], [1, 3, 4], [1, 3, 5], [1, 4, 5], [2, 3, 4], [2, 3, 5], [2, 4, 5], [3, 4, 5]]; @png begin setopacity(0.2) pentachoron2D = flatten(pentachoron) for (n, face) in enumerate(pentachoronfaces) randomhue() poly(1500 * pentachoron2D[face], :fillpreserve, close=true) sethue("black") strokepath() end end 300 250 "5ceil"

Chaque développeur de jeu qui se respecte devrait connaître les principes mathématiques de la machine graphique . Si vous n'avez jamais essayé de compresser, faire pivoter, refléter des théières dans OpenGL - ne vous inquiétez pas, tout est assez simple. Pour refléter un point par rapport à une ligne droite ou pour faire pivoter un plan autour d'un certain axe, vous devez multiplier les coordonnées par une matrice spéciale. En fait plus loin, nous déterminerons les matrices de transformation dont nous avons besoin:
ramasser plus function XY(θ) [cos(θ) -sin(θ) 0 0; sin(θ) cos(θ) 0 0; 0 0 1 0; 0 0 0 1] end function XW(θ) [cos(θ) 0 0 -sin(θ); 0 1 0 0; 0 0 1 0; sin(θ) 0 0 cos(θ)] end function XZ(θ) [cos(θ) 0 -sin(θ) 0; 0 1 0 0; sin(θ) 0 cos(θ) 0; 0 0 0 1] end function YZ(θ) [1 0 0 0; 0 cos(θ) -sin(θ) 0; 0 sin(θ) cos(θ) 0; 0 0 0 1] end function YW(θ) [1 0 0 0; 0 cos(θ) 0 -sin(θ); 0 0 1 0; 0 sin(θ) 0 cos(θ)] end function ZW(θ) [1 0 0 0; 0 1 0 0; 0 0 cos(θ) -sin(θ); 0 0 sin(θ) cos(θ)]; end function rotate4(A, matrixfunction) return map(A) do pt4 Point4D(matrixfunction * pt4) end end
Habituellement, vous faites pivoter des points sur un plan par rapport à un objet unidimensionnel. Les points 3D sont autour d'une ligne 2D (souvent c'est l'un des axes XYZ). Ainsi, il est logique que les points 4D tournent par rapport au plan 3D. Nous avons identifié des matrices qui effectuent une rotation en quatre dimensions autour d'un plan défini par deux axes X, Y, Z et W. Le plan XY est généralement le plan de la surface de dessin. Si vous percevez le plan XY comme un écran d'ordinateur, alors le plan XZ est parallèle à votre table ou votre sol, et le plan YZ est le mur à côté de votre table à droite ou à gauche. Mais qu'en est-il de XW, YW et ZW? C'est le mystère des figures à quatre dimensions: nous ne pouvons pas voir ces plans, nous pouvons seulement imaginer leur existence en observant comment les formes se déplacent à travers eux et autour d'eux.
Maintenant, nous définissons les fonctions des images et cousons l'animation:
spoiler using ColorSchemes function frame(scene, framenumber, scalefactor=1000) background("white")

Eh bien, et un autre angle:
Code function frame(scene, framenumber, scalefactor=1000) background("antiquewhite") setlinejoin("bevel") setline(1.0) setopacity(0.2) eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop) pentachoron2D = flatten( rotate4( pentachoron, XZ(eased_n * 2π) * YW(eased_n * 2π))) for (n, face) in enumerate(pentachoronfaces) sethue(get(ColorSchemes.diverging_rainbow_bgymr_45_85_c67_n256, n/length(pentachoronfaces))) poly(scalefactor * pentachoron2D[face], :fillpreserve, close=true) sethue("black") strokepath() end end makemovie(500, 500, "pentachoron-xz-yw.gif", scalefactor=2000)
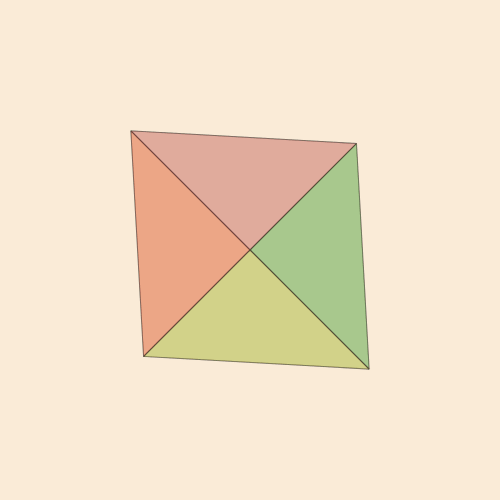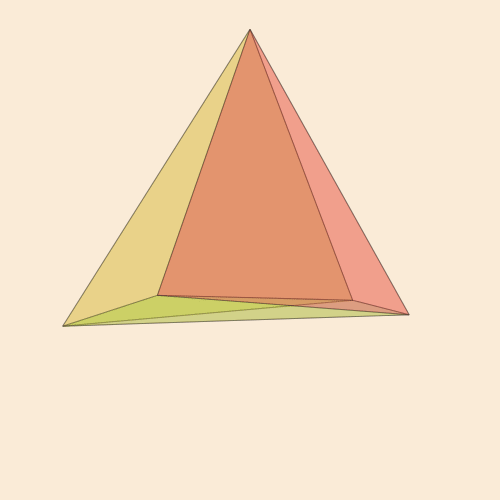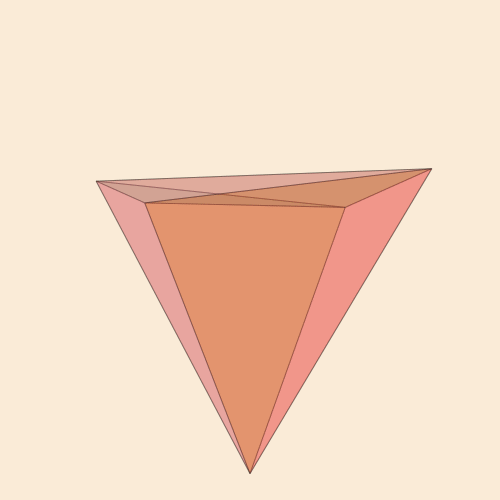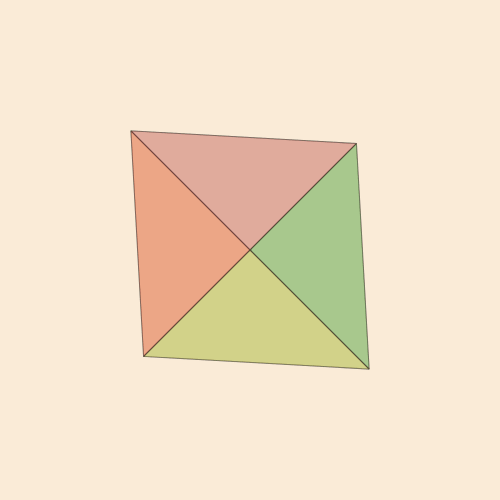
Le désir de réaliser un objet à quatre dimensions plus populaire, le Tesseract, est tout à fait naturel.
Hauts et visages const tesseract = [Point4D(vertex...) for vertex in [ [-1, -1, -1, 1], [ 1, -1, -1, 1], [ 1, 1, -1, 1], [-1, 1, -1, 1], [-1, -1, 1, 1], [ 1, -1, 1, 1], [ 1, 1, 1, 1], [-1, 1, 1, 1], [-1, -1, -1, -1], [ 1, -1, -1, -1], [ 1, 1, -1, -1], [-1, 1, -1, -1], [-1, -1, 1, -1], [ 1, -1, 1, -1], [ 1, 1, 1, -1], [-1, 1, 1, -1]]] const tesseractfaces = [ [1, 2, 3, 4], [1, 2, 10, 9], [1, 4, 8, 5], [1, 5, 6, 2], [1, 9, 12, 4], [2, 3, 11, 10], [2, 3, 7, 6], [3, 4, 8, 7], [5, 6, 14, 13], [5, 6, 7, 8], [5, 8, 16, 13], [6, 7, 15, 14], [7, 8, 16, 15], [9, 10, 11, 12], [9, 10, 14, 13], [9, 13, 16, 12], [10, 11, 15, 14], [13, 14, 15, 16]];
Créer une animation function frame(scene, framenumber, scalefactor=1000) background("black") setlinejoin("bevel") setline(10.0) setopacity(0.7) eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop) tesseract2D = flatten( rotate4( tesseract, XZ(eased_n * 2π) * YW(eased_n * 2π))) for (n, face) in enumerate(tesseractfaces) sethue([Luxor.lighter_blue, Luxor.lighter_green, Luxor.lighter_purple, Luxor.lighter_red][mod1(n, 4)]...) poly(scalefactor * tesseract2D[face], :fillpreserve, close=true) sethue([Luxor.darker_blue, Luxor.darker_green, Luxor.darker_purple, Luxor.darker_red][mod1(n, 4)]...) strokepath() end end makemovie(500, 500, "tesseract-xz-yw.gif", scalefactor=1000)

Devoirs: automatisez la création de tableaux de coordonnées et de nombres de sommets ( permutations avec répétitions et sans répétitions, respectivement ). De plus, nous n'avons pas utilisé toutes les matrices de traduction; Chaque nouvelle perspective fait apparaître un nouveau «Wow!», Mais j'ai décidé de ne pas surcharger la page. Eh bien, vous pouvez expérimenter de nombreux visages et dimensions.
Les références