Suppression du bruit haute fréquence des signaux des capteurs de vibrations lors du diagnostic des vibrations des roulements

Photo prise de la publication

Présentation

L'une des tâches les plus urgentes du traitement numérique du signal est de nettoyer le signal du bruit. Tout signal pratique contient non seulement des informations utiles, mais également des traces de certains effets externes d'interférences ou de bruit. De plus, lors des diagnostics de vibrations, les signaux des capteurs de vibrations ont un spectre de fréquences non stationnaire, ce qui complique la tâche de filtrage.

Il existe de nombreuses façons différentes de supprimer le bruit haute fréquence d'un signal. Par exemple, la bibliothèque Scipy contient des filtres basés sur diverses méthodes de filtrage: Kalman; lisser le signal en le faisant la moyenne le long de l'axe du temps, et autres.

Cependant, l'avantage de la méthode de transformation en ondelettes discrètes (DWT) est la variété des formes d'ondelettes. Vous pouvez sélectionner une ondelette, qui aura une forme caractéristique des phénomènes attendus. Par exemple, vous pouvez sélectionner un signal dans une gamme de fréquences donnée, dont la forme est responsable de l'apparition d'un défaut.

Le but de cette publication est d'analyser les méthodes de filtrage des signaux des capteurs de vibration en utilisant la conversion de signal DWT, le filtre de Kalman et la méthode de la moyenne mobile.

Données source pour l'analyse

Dans la publication, le fonctionnement des filtres basés sur diverses méthodes de filtrage sera analysé à l'aide d' un ensemble de données de la NASA . Données obtenues sur la plateforme expérimentale PRONOSTIA:



Le kit contient des données sur les signaux des capteurs de vibration pour l'usure de divers types de roulements. La fonction des dossiers contenant les fichiers de signaux est indiquée dans le tableau :



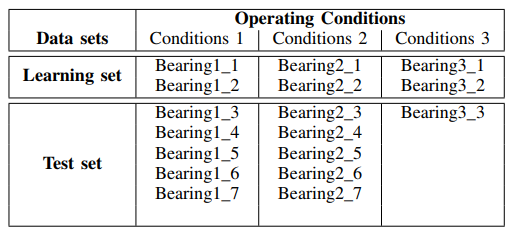
La surveillance de l'état des roulements est assurée par les signaux des capteurs de vibration (accéléromètres horizontaux et verticaux), la force et la température.



Signaux reçus pour trois charges différentes:

• Premières conditions de travail: 1800 tr / min et 4000 N;
• Deuxième conditions de travail: 1650 tr / min et 4200 N;
• Troisième conditions de fonctionnement: 1500 tr / min et 5000 N.

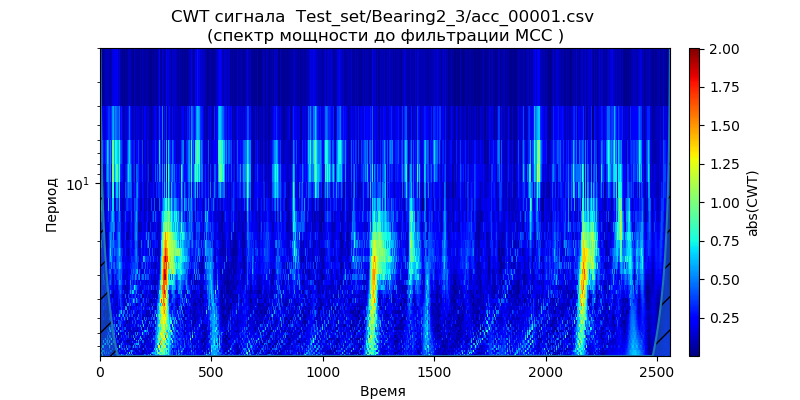
Pour ces conditions, en utilisant la conversion continue du signal en ondelettes, nous construisons les scalogrammes de puissance spectrale pour les données de l'ensemble de test - un fichier (pour un type de roulements) à partir des dossiers: ['Test_set / Bearing1_3 / acc_00001.csv', 'Test_set / Bearing2_3 / acc_00001. csv ',' Test_set / Bearing3_3 / acc_00001.csv '] (voir tableau 1).






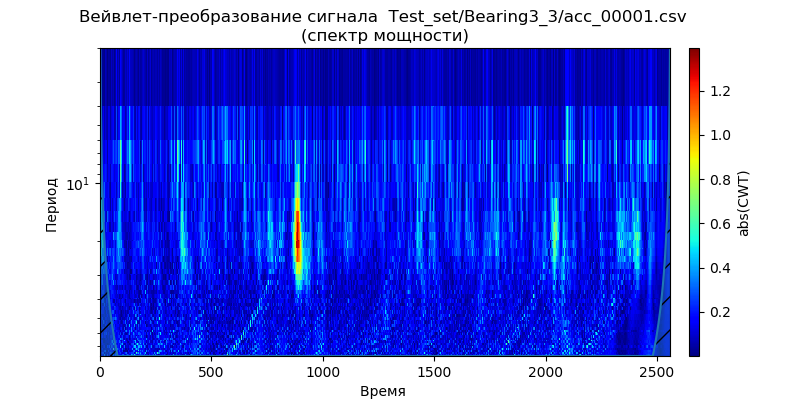
Il résulte des scalogrammes donnés que les moments d'augmentation de la puissance du spectre apparaissent plus tôt dans le temps et démontrent la fréquence des conditions de fonctionnement: 1650 tr / min et 4200 N, ce qui indique une dégradation accélérée des roulements dans cette bande de fréquence pour la force réduite. Nous utiliserons ce signal ('Test_set / Bearing2_3 / acc_00001.csv') pour analyser les méthodes d'élimination du bruit.

Déconstruction du signal à l'aide de DWT

Dans la publication, nous avons vu comment un banc de filtres est implémenté sur le DWT qui peut déconstruire un signal dans ses sous-bandes de fréquence. Les coefficients d'approximation (cA) représentent la partie basse fréquence du signal (filtre de moyenne). Les coefficients de détail (cD) représentent la partie haute fréquence du signal. Ensuite, nous examinerons comment le DWT peut être utilisé pour déconstruire un signal dans ses sous-bandes de fréquence et restaurer le signal d'origine.

Il existe deux façons de résoudre le problème de déconstruction du signal à l'aide des outils PyWavelets:

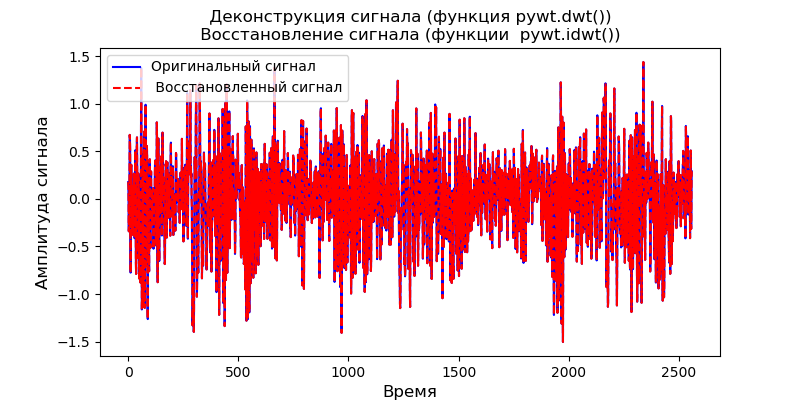
La première consiste à appliquer pywt.dwt () au signal pour extraire les coefficients d'approximation et de détail (cA1, cD1). Ensuite, pour restaurer le signal, nous utiliserons pywt.idwt ():




La deuxième façon d'appliquer la fonction pywt.wavedec () au signal est de restaurer tous les coefficients d'approximation et de détail à un certain niveau. Cette fonction prend le signal d'entrée et le niveau en entrée et renvoie un ensemble de coefficients d'approximation (nième niveau) et n ensembles de coefficients de détail (de 1 à nième niveau). Pour la déconstruction, appliquez pywt.waverec ():



La deuxième façon de déconstruire et de restaurer le signal est plus pratique, elle vous permet de définir immédiatement le niveau de déconstruction souhaité.

Suppression du bruit haute fréquence en éliminant certains des coefficients de détail lors de la déconstruction du signal

Nous allons restaurer le signal en supprimant certains des coefficients de détail. Étant donné que les coefficients de détail représentent la partie haute fréquence du signal, nous filtrons simplement cette partie du spectre de fréquence. S'il y a du bruit haute fréquence dans le signal, c'est une façon de le filtrer.

Dans la bibliothèque PyWavelets, cela peut être fait en utilisant la fonction de traitement de seuil pywt.threshol ():

pywt.threshold (data, value, mode = 'soft', substitute = 0) ¶
données: array_like
Données numériques.
valeur: scalaire
Valeur seuil.
mode: {'doux', 'dur', 'garrote', 'plus grand', 'moins'}
Définit le type de seuil qui sera appliqué à l'entrée. La valeur par défaut est «douce».
substitut: flotteur, facultatif
Valeur de substitution (par défaut: 0).
sortie: tableau
Tableau de seuil.

L'application de la fonction de traitement de seuil pour une valeur de seuil donnée est mieux envisagée à l'aide de l'exemple suivant:

 >>>> from scipy import* >>> import pywt >>> data =linspace(1, 4, 7) >>> data array([1. , 1.5, 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'soft') array([0. , 0. , 0. , 0.5, 1. , 1.5, 2. ]) >>> pywt.threshold(data, 2, 'hard') array([0. , 0. , 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'garrote') array([0. , 0. , 0., 0.9,1.66666667, 2.35714286, 3.]) 

Nous traçons le graphique de la fonction de seuil à l'aide de la liste suivante:



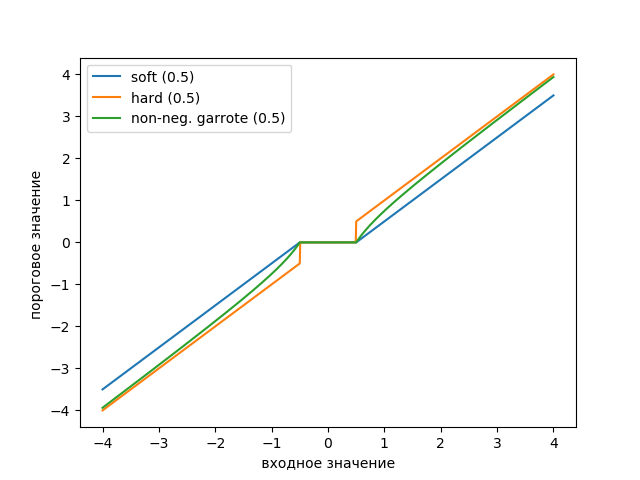
Le graphique montre que le seuil de Garott non négatif est intermédiaire entre le seuil doux et dur. Une paire de seuils est nécessaire pour définir la largeur de la région de transition.

L'influence de la fonction de seuil sur les caractéristiques du filtre

Comme il ressort du graphique ci-dessus, seules deux fonctions de seuil «soft» et «garrote» nous conviennent, pour étudier leur influence sur les caractéristiques du filtre, nous notons la liste:





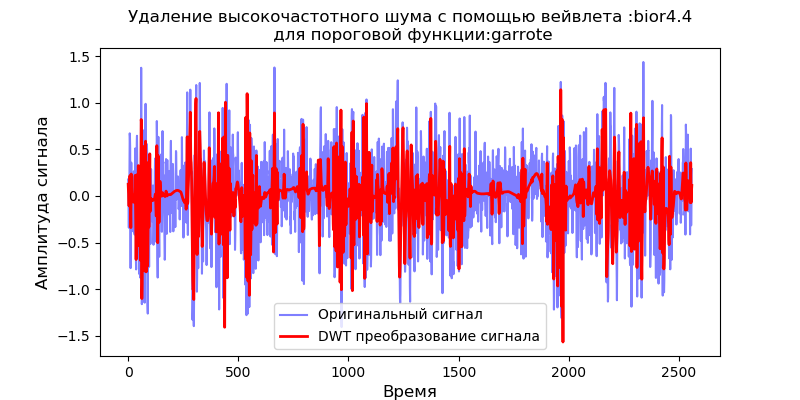
Comme il ressort des graphiques, la fonction douce offre un meilleur lissage que la fonction «garrote», nous utiliserons donc la fonction douce à l'avenir.

L'influence du seuil de détail sur les caractéristiques du filtre

Pour le type de filtre considéré, le seuil de modification des coefficients de détail est une caractéristique importante, nous étudions donc son effet à l'aide de la liste suivante:






Comme il ressort des graphiques obtenus, le seuil de niveau de détail affecte l'échelle des pièces filtrées. Avec une augmentation du seuil, l'ondelette soustrait le bruit d'un niveau toujours croissant jusqu'à ce qu'un agrandissement excessif de l'échelle de détail se produise et que la transformation commence à déformer la forme du signal d'origine. Pour notre signal, le seuil ne doit pas être supérieur à 0,63.

L'effet des ondelettes sur les caractéristiques du filtre

La bibliothèque PyWavelets a un nombre suffisant d'ondelettes pour la conversion DWT, qui peuvent être obtenues comme ceci:

 >>> import pywt >>> print(pywt.wavelist(kind= 'discrete')) ['bior1.1', 'bior1.3', 'bior1.5', 'bior2.2', 'bior2.4', 'bior2.6', 'bior2.8', 'bior3.1', 'bior3.3', 'bior3.5', 'bior3.7', 'bior3.9', 'bior4.4', 'bior5.5', 'bior6.8', 'coif1', 'coif2', 'coif3', 'coif4', 'coif5', 'coif6', 'coif7', 'coif8', 'coif9', 'coif10', 'coif11', 'coif12', 'coif13', 'coif14', 'coif15', 'coif16', 'coif17', 'db1', 'db2', 'db3', 'db4', 'db5', 'db6', 'db7', 'db8', 'db9', 'db10', 'db11', 'db12', 'db13', 'db14', 'db15', 'db16', 'db17', 'db18', 'db19', 'db20', 'db21', 'db22', 'db23', 'db24', 'db25', 'db26', 'db27', 'db28', 'db29', 'db30', 'db31', 'db32', 'db33', 'db34', 'db35', 'db36', 'db37', 'db38', 'dmey', 'haar', 'rbio1.1', 'rbio1.3', 'rbio1.5', 'rbio2.2', 'rbio2.4', 'rbio2.6', 'rbio2.8', 'rbio3.1', 'rbio3.3', 'rbio3.5', 'rbio3.7', 'rbio3.9', 'rbio4.4', 'rbio5.5', 'rbio6.8', 'sym2', 'sym3', 'sym4', 'sym5', 'sym6', 'sym7', 'sym8', 'sym9', 'sym10', 'sym11', 'sym12', 'sym13', 'sym14', 'sym15', 'sym16', 'sym17', 'sym18', 'sym19', 'sym20'] 

L'influence de l'ondelette sur la caractéristique du filtre dépend de sa fonction primitive. Pour démontrer cette dépendance, nous sélectionnons deux ondelettes de la famille Dobeshi - db1 et db38, et considérons ces familles:




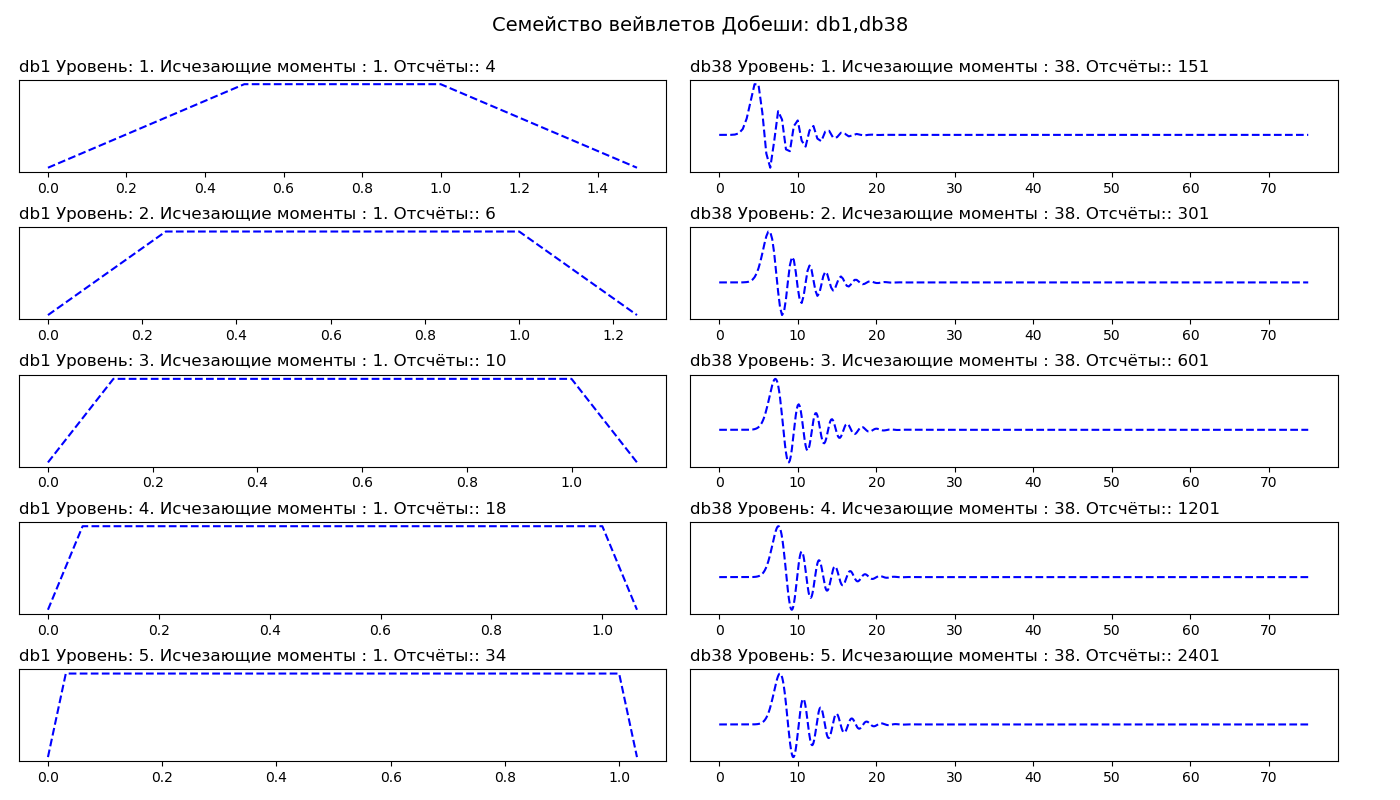
Dans la première colonne, nous voyons des ondelettes de Daubeshi du premier ordre (db1), dans la deuxième colonne du trente-huitième ordre (db38). Ainsi, db1 a un moment d'extinction et db38 a 38 moments d'extinction. Le nombre de moments de disparition est lié à l'ordre d'approximation et au lissé de l'ondelette. Si une ondelette a P points de disparition, elle peut se rapprocher des polynômes de degré P - 1.

Des ondelettes plus lisses créent une approximation de signal plus douce, et vice versa - des ondelettes «courtes» suivent mieux les pics de la fonction approchée. Lors du choix d'une ondelette, nous pouvons également indiquer quel doit être le niveau de décomposition. Par défaut, PyWavelets sélectionne le niveau de décomposition maximum possible pour le signal d'entrée. Le niveau de décomposition maximum dépend de la longueur du signal d'entrée et de l'ondelette:


Pour ondelette db1, niveau de décomposition maximum: 11
Pour ondelette db38, niveau de décomposition maximum: 5

Pour les valeurs obtenues des niveaux maximaux de décomposition en ondelettes, nous considérons le fonctionnement du filtre pour éliminer le bruit haute fréquence:









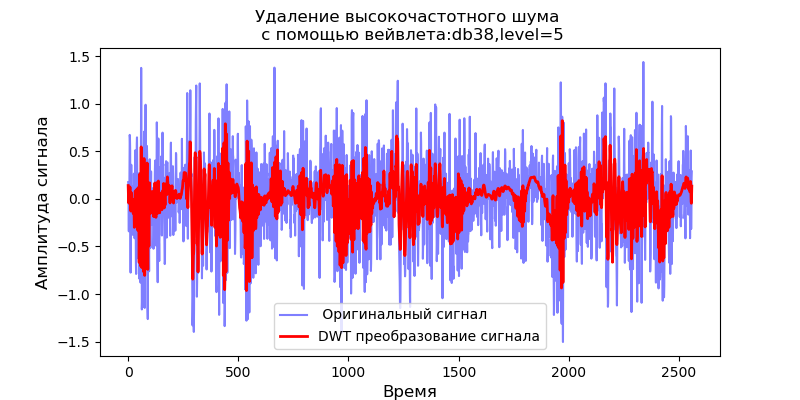
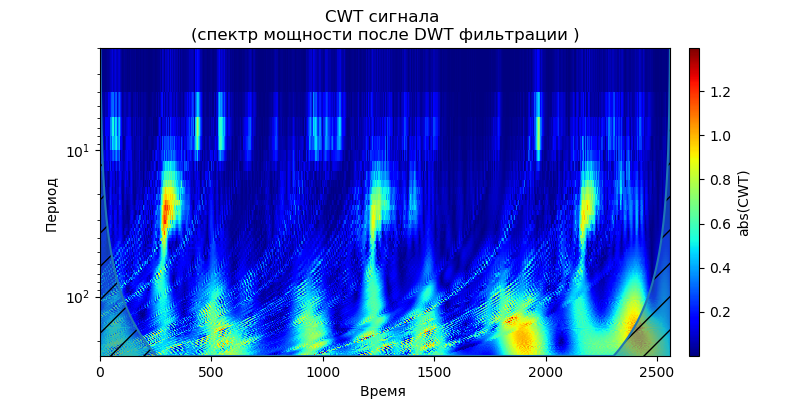
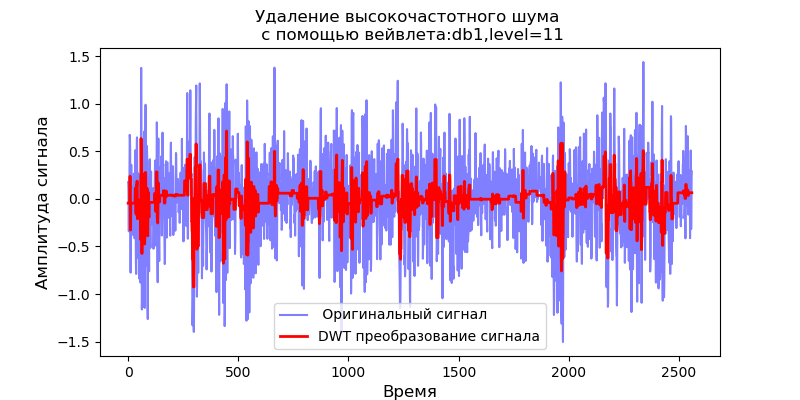
Il résulte des scalogrammes donnés des signaux à la sortie du filtre que, pour l'ondelette db38, la puissance de crête du spectre est suivie de régions localisées, pour l'ondelette db1 ces régions disparaissent. Vous pouvez choisir une ondelette dont la fonction antidérivative aura une forme caractéristique des phénomènes que nous attendons. Il convient de noter que, par exemple, l'ondelette db38 peut se rapprocher d'un signal de polynôme de degré 37. Cela étend la classification des signaux, par exemple, pour identifier les dysfonctionnements des équipements en fonction des signaux des capteurs de vibrations.

Étant donné que le signal après le filtre avec l'ondelette de Daubechies forme une série temporelle utilisant des coefficients d'approximation et de décomposition comme caractéristiques de la série, on peut déterminer le degré de proximité de ces séries, ce qui simplifie considérablement leur recherche et leur classification

Filtre de Kalman pour éliminer le bruit haute fréquence

Le filtre de Kalman est largement utilisé pour filtrer le bruit dans divers systèmes dynamiques. Considérons un système dynamique avec un vecteur d'état x.

$$$x = F \ cdot x + w (Q)$

où F est la matrice de transition
w (Q) est un processus aléatoire (bruit) avec une attente mathématique nulle et une matrice de covariance Q.

Nous observerons les transitions d'état du système avec une erreur de mesure connue à chaque instant. L'élimination du bruit à l'aide de la méthode de Kalman se compose de deux étapes - extrapolation et correction, cela ressemble à ceci.

Définissez les paramètres du système:

Matrice Q de covariance de bruit (covariance de bruit de processus).
H est la matrice d'observation (mesure).
R - covariance du bruit d'observation (covariance du bruit de mesure).
P = Q est la valeur initiale de la matrice de covariance pour le vecteur d'état.
z (t) est l'état observé du système.
x = z (0) est la valeur initiale de l'état du système.

Pour chaque observation z, nous calculerons l'état filtré x
et pour cela, nous effectuons les étapes suivantes.

• étape 1: extrapolation
1. extrapolation (prédiction) de l'état du système
$$$x = F \ cdot x$
2. calculer la matrice de covariance pour le vecteur d'état extrapolé
$$$F = F \ cdot P \ cdot F ^ {T} + Q$

• étape 2: correction
1. calculer le vecteur d'erreur, l'écart de l'observation par rapport à l'état attendu
$$$y = z-H \ cdot x$
2. calculer la matrice de covariance pour le vecteur de déviation (vecteur d'erreur)
$$$S = H \ cdot P \ cdot H ^ {T} + R$
3. calculer les gains de Kalman
$$$K = P \ cdot H \ cdot H ^ {T} \ cdot S ^ {- 1}$
4. correction de l'estimation du vecteur d'état
$$$x = x + K \ cdot y$
5. nous corrigeons la matrice de covariance pour estimer le vecteur d'état du système
$$$P = (I-K \ cdot H) \ cdot P$




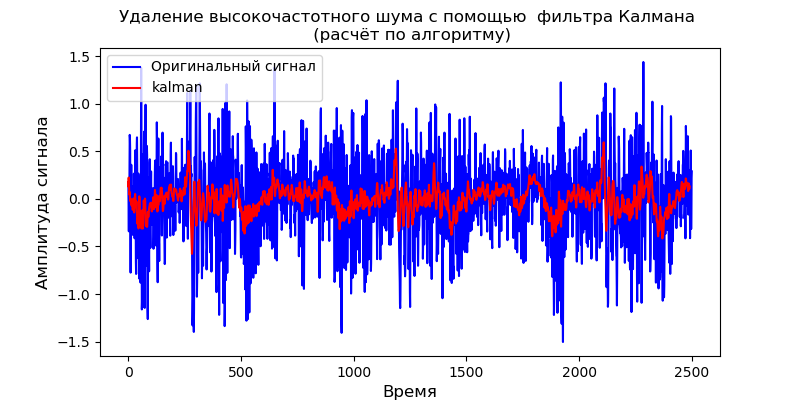
Pour le modèle dynamique donné, vous pouvez utiliser la bibliothèque pyKalman:






Le filtre de Kalman élimine bien le bruit haute fréquence, cependant, il ne permet pas de changer la forme du signal de sortie.

Méthode moyenne mobile

En déterminant la direction principale des changements dans une séquence fortement oscillante, le problème se pose de l'aplanir en utilisant la méthode de la moyenne mobile. Cela peut être les lectures du capteur de niveau de carburant dans la voiture ou, comme dans notre cas, les données des capteurs haute fréquence concernant la dégradation accélérée des roulements. Le problème peut être considéré comme la restauration d'une séquence r à laquelle le bruit s'est superposé.

Moyenne mobile simple pour court - SMA (moyenne mobile simple). Pour calculer la valeur actuelle du filtre $$$r_ {i}$ nous faisons simplement la moyenne des n éléments précédents de la séquence, de sorte que le filtre commence à fonctionner avec l'élément de séquence n.

$$$r_ {i} = \ frac {1} {n} \ cdot \ sum_ {j = 1} ^ {n} y _ {(i-j)}; i> n$






Comme il ressort du scalogramme, la méthode SMA ne nettoie pas le signal du bruit haute fréquence,
comme mentionné ci-dessus est utilisé pour le lissage.

Conclusions:

1. En utilisant le module scalogramme, des scalogrammes en ondelettes CWT de trois signaux de capteur de vibration d'essai ont été obtenus pour différentes conditions d'essai pour des roulements du même type. Selon les données du scalogramme, un signal présentant des signes clairement exprimés de dégradation tardive a été sélectionné. Ce signal a été utilisé pour démontrer le fonctionnement des filtres dans tous les exemples donnés.
2. Les méthodes de la bibliothèque PyWavelets pour la déconstruction DWT et la restauration du signal du capteur de vibration utilisant les modules pywt.dwt (), pywt.idwt () et le module pywt.wavedec () pour un niveau d'ondelettes donné sont considérées.
3. Les exemples illustrent les fonctionnalités d'application du module pywt.threshol () pour filtrer les coefficients de détail DWT, qui sont responsables de la partie haute fréquence du spectre à l'aide de fonctions de seuil pour une valeur de seuil donnée.
4. Les effets de l'ondelette DWT anti-dérivative sur la forme d'un signal débarrassé du bruit sont considérés.
5. On obtient un modèle de filtre de Kalman pour un milieu dynamique, le modèle est testé sur le signal de test du capteur de vibration. Le tracé d'élimination du bruit est le même que celui obtenu à l'aide du module pyKalman. La nature du graphique coïncide avec le scalogramme.
6. .