
La traduction de l'article a été préparée spécialement pour les étudiants du cours "Algorithmes pour les développeurs" .
Le tri par pyramide (ou tri par tas, HeapSort) est une méthode de tri par comparaison basée sur une structure de données telle qu'un tas binaire. Il est similaire au tri par sélection, où nous recherchons d'abord l'élément maximum et le mettons à la fin. Ensuite, nous répétons la même opération pour les éléments restants.
Définissons d'abord un arbre binaire complet. Un arbre binaire fini est un arbre binaire dans lequel chaque niveau, à l'exception peut-être du dernier, a un ensemble complet de nœuds, et toutes les feuilles sont situées à gauche (Source Wikipedia ).
Un segment binaire est un arbre binaire complet dans lequel les éléments sont stockés dans un ordre spécial: la valeur dans le nœud parent est supérieure (ou inférieure) aux valeurs de ses deux nœuds enfants. La première option est appelée max-tas et la seconde est min-tas. Un tas peut être représenté par un arbre binaire ou un tableau.
Pourquoi la représentation basée sur un tableau est-elle utilisée pour le tas binaire?
Étant donné que le segment binaire est un arbre binaire complet, il peut être facilement représenté sous forme de tableau et la représentation basée sur un tableau est efficace en termes de consommation de mémoire. Si le nœud parent est stocké dans l'index I, l'enfant gauche peut être calculé comme 2 I + 1 et l'enfant droit peut être calculé comme 2 I + 2 (à condition que l'indexation commence à 0).
Algorithme de tri pyramidal en ordre croissant:
- Construisez max-heap à partir de l'entrée.
- À ce stade, le plus grand élément est stocké à la racine du tas. Remplacez-le par le dernier élément du tas, puis réduisez sa taille de 1. Enfin, convertissez l'arborescence résultante en max-tas avec une nouvelle racine.
- Répétez les étapes ci-dessus jusqu'à ce que la taille du tas soit supérieure à 1.
Comment construire un tas?
La procédure de conversion de tas (ci-après dénommée la procédure de tas) ne peut être appliquée à un nœud que si ses nœuds enfants sont déjà convertis. Ainsi, la conversion doit être effectuée de bas en haut. Voyons cela avec un exemple:
: 4, 10, 3, 5, 1 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4) . heapify 1: 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4) heapify 0: 10(0) / \ 5(1) 3(2) / \ 4(3) 1(4) heapify .
Recommandation: veuillez d'abord résoudre le problème sur «PRATIQUE» avant de procéder à la solution .
C ++
// C++ #include <iostream> using namespace std; // i, // arr[]. n - void heapify(int arr[], int n, int i) { int largest = i; // int l = 2*i + 1; // = 2*i + 1 int r = 2*i + 2; // = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { swap(arr[i], arr[largest]); // heapify(arr, n, largest); } } // , void heapSort(int arr[], int n) { // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // swap(arr[0], arr[i]); // heapify heapify(arr, i, 0); } } /* n*/ void printArray(int arr[], int n) { for (int i=0; i<n; ++i) cout << arr[i] << " "; cout << "\n"; } // int main() { int arr[] = {12, 11, 13, 5, 6, 7}; int n = sizeof(arr)/sizeof(arr[0]); heapSort(arr, n); cout << "Sorted array is \n"; printArray(arr, n); }
Java
// Java public class HeapSort { public void sort(int arr[]) { int n = arr.length; // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // heapify heapify(arr, i, 0); } } // i, // arr[]. n - void heapify(int arr[], int n, int i) { int largest = i; // int l = 2*i + 1; // = 2*i + 1 int r = 2*i + 2; // = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; // heapify(arr, n, largest); } } /* n */ static void printArray(int arr[]) { int n = arr.length; for (int i=0; i<n; ++i) System.out.print(arr[i]+" "); System.out.println(); } // public static void main(String args[]) { int arr[] = {12, 11, 13, 5, 6, 7}; int n = arr.length; HeapSort ob = new HeapSort(); ob.sort(arr); System.out.println("Sorted array is"); printArray(arr); } }
Python
# Python # i, arr[]. n - def heapify(arr, n, i): largest = i # Initialize largest as root l = 2 * i + 1 # left = 2*i + 1 r = 2 * i + 2 # right = 2*i + 2 # , if l < n and arr[i] < arr[l]: largest = l # , if r < n and arr[largest] < arr[r]: largest = r # , if largest != i: arr[i],arr[largest] = arr[largest],arr[i] # # heapify . heapify(arr, n, largest) # def heapSort(arr): n = len(arr) # max-heap. for i in range(n, -1, -1): heapify(arr, n, i) # for i in range(n-1, 0, -1): arr[i], arr[0] = arr[0], arr[i] # heapify(arr, i, 0) # arr = [ 12, 11, 13, 5, 6, 7] heapSort(arr) n = len(arr) print ("Sorted array is") for i in range(n): print ("%d" %arr[i]), # Mohit Kumra
C forte
// C# using System; public class HeapSort { public void sort(int[] arr) { int n = arr.Length; // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // heapify heapify(arr, i, 0); } } // i, // arr[]. n - void heapify(int[] arr, int n, int i) { int largest = i; // int l = 2*i + 1; // left = 2*i + 1 int r = 2*i + 2; // right = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; // heapify(arr, n, largest); } } /* n */ static void printArray(int[] arr) { int n = arr.Length; for (int i=0; i<n; ++i) Console.Write(arr[i]+" "); Console.Read(); } // public static void Main() { int[] arr = {12, 11, 13, 5, 6, 7}; int n = arr.Length; HeapSort ob = new HeapSort(); ob.sort(arr); Console.WriteLine("Sorted array is"); printArray(arr); } } // // Akanksha Ra (Abby_akku)
Php
<?php // Php // i, // arr[]. n - function heapify(&$arr, $n, $i) { $largest = $i; // $l = 2*$i + 1; // = 2*i + 1 $r = 2*$i + 2; // = 2*i + 2 // if ($l < $n && $arr[$l] > $arr[$largest]) $largest = $l; // , if ($r < $n && $arr[$r] > $arr[$largest]) $largest = $r; // if ($largest != $i) { $swap = $arr[$i]; $arr[$i] = $arr[$largest]; $arr[$largest] = $swap; // heapify($arr, $n, $largest); } } // , function heapSort(&$arr, $n) { // ( ) for ($i = $n / 2 - 1; $i >= 0; $i--) heapify($arr, $n, $i); // for ($i = $n-1; $i >= 0; $i--) { // $temp = $arr[0]; $arr[0] = $arr[$i]; $arr[$i] = $temp; // heapify heapify($arr, $i, 0); } } /* n */ function printArray(&$arr, $n) { for ($i = 0; $i < $n; ++$i) echo ($arr[$i]." ") ; } // $arr = array(12, 11, 13, 5, 6, 7); $n = sizeof($arr)/sizeof($arr[0]); heapSort($arr, $n); echo 'Sorted array is ' . "\n"; printArray($arr , $n); // Shivi_Aggarwal ?>
Conclusion:
: 5 6 7 11 12 13
Voici le code C précédent pour référence.
Remarques:
Le tri pyramidal est un algorithme parfaitement adapté. Son implémentation typique n'est pas stable, mais peut se faire en tant que telle (voir ici ).
Complexité temporelle: La complexité temporelle de heapify est O (Logn). La complexité temporelle de createAndBuildHeap () est O (n) et la durée d'exécution totale du tri pyramidal est O (nLogn).
Applications de tri pyramidal:
- Trier un tableau presque trié (ou trié par K positions) ;
- k les plus grands (ou les plus petits) éléments du tableau .
L'algorithme de tri pyramidal a une utilisation limitée, car Quicksort et Mergesort sont meilleurs en pratique. Cependant, la structure de données du tas elle-même est utilisée assez souvent. Voir Applications de structure de données de tas
Captures d'écran:
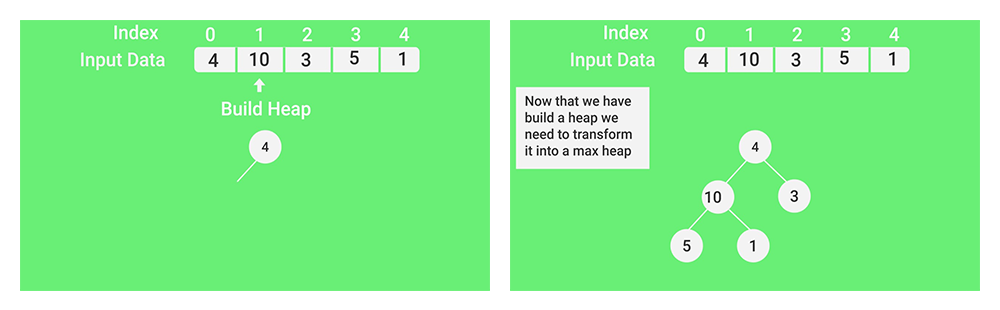
- (Maintenant que nous avons construit le tas, nous devons le convertir en max-tas)

- (Dans max-heap, le nœud parent est toujours supérieur ou égal aux nœuds enfants
10 de plus que 4. Par conséquent, nous échangeons 4 et 10)
- (Dans max-heap, le nœud parent est toujours supérieur ou égal aux nœuds enfants
5 plus 4. Par conséquent, nous échangeons les places 5 et 4)

- (Échangez les premier et dernier nœuds et supprimez le dernier du tas)
Test de pyramide
Autres algorithmes de tri sur GeeksforGeeks / GeeksQuiz:
Tri rapide , Tri par sélection , Tri par bulles, Tri par insertion, Tri par fusion, Tri par pyramide, Tri par bits, Tri par comptage, Tri par bloc, Tri par coque, Tri par peigne, Tri par comptage avec liste .
Atelier de tri
Veuillez laisser des commentaires si vous trouvez quelque chose de mal ou si vous souhaitez partager des informations supplémentaires sur le sujet discuté ci-dessus.