
La science des données devient une partie intégrante de toute activité marketing, et ce livre est un portrait vivant de la transformation numérique dans le marketing. L'analyse des données et des algorithmes intelligents automatisent les tâches de marketing chronophages. Le processus décisionnel devient non seulement plus parfait, mais aussi plus rapide, ce qui est d'une grande importance dans un environnement concurrentiel en constante accélération.
«Ce livre est un portrait vivant de la transformation numérique en marketing. Il montre comment la science des données devient une partie intégrante de toute activité marketing. Il décrit en détail comment les approches basées sur l'analyse des données et les algorithmes intelligents contribuent à l'automatisation profonde des tâches marketing traditionnellement à forte intensité de main-d'œuvre. Le processus décisionnel devient non seulement plus avancé, mais aussi plus rapide, ce qui est important dans notre environnement concurrentiel en constante accélération. Ce livre doit être lu par des spécialistes de l'informatique et des spécialistes du marketing, et il vaut mieux qu'ils le lisent ensemble. » Andrey Sebrant, directeur du marketing stratégique, Yandex.
Extrait. 5.8.3. Modèles à facteurs cachés
Dans les algorithmes de filtrage conjoints examinés jusqu'à présent, la plupart des calculs sont basés sur les éléments individuels de la matrice de notation. Les méthodes basées sur la proximité évaluent les notes manquantes directement à partir des valeurs connues dans la matrice de notation. Les méthodes basées sur un modèle ajoutent une couche d'abstraction au-dessus de la matrice de notation, créant un modèle prédictif qui capture certains modèles de relations entre les utilisateurs et les éléments, mais la formation du modèle dépend toujours fortement des propriétés de la matrice de notation. Par conséquent, ces techniques de filtrage collaboratif sont généralement confrontées aux problèmes suivants:
La matrice de notation peut contenir des millions d'utilisateurs, des millions d'éléments et des milliards de notes connues, ce qui crée de graves problèmes de complexité et d'évolutivité des calculs.
La matrice de notation est généralement très clairsemée (en pratique, environ 99% des notations peuvent manquer). Cela affecte la stabilité de calcul des algorithmes de recommandation et conduit à des estimations peu fiables lorsque l'utilisateur ou l'élément n'a pas de voisins vraiment similaires. Ce problème est souvent aggravé par le fait que la plupart des algorithmes de base sont orientés utilisateur ou élément, ce qui limite leur capacité à enregistrer tous les types de similitudes et de relations disponibles dans la matrice de notation.
Les données de la matrice de notation sont généralement fortement corrélées en raison des similitudes entre les utilisateurs et les éléments. Cela signifie que les signaux disponibles dans la matrice de notation sont non seulement clairsemés, mais également redondants, ce qui contribue à l'aggravation du problème d'évolutivité.
Les considérations ci-dessus indiquent que la matrice de notation d'origine peut ne pas être la représentation la plus optimale des signaux, et d'autres représentations alternatives qui conviennent mieux au filtrage conjoint devraient être envisagées. Pour explorer cette idée, revenons au point de départ et réfléchissons un peu à la nature des services de recommandation. En fait, le service de recommandation peut être considéré comme un algorithme de prévision des évaluations basé sur une certaine mesure de similitude entre l'utilisateur et l'élément:
Une façon de déterminer cette mesure de similitude consiste à utiliser l'approche des facteurs cachés et à mapper les utilisateurs et les éléments à des points dans un espace k-dimensionnel afin que chaque utilisateur et chaque élément soit représenté par un vecteur k-dimensionnel:
Les vecteurs doivent être construits de manière à ce que les dimensions correspondantes p et q soient comparables. En d'autres termes, chaque dimension peut être considérée comme un signe ou un concept, c'est-à-dire que puj est une mesure de proximité de l'utilisateur u et du concept j, et qij, respectivement, est une mesure de l'élément i et du concept j. Dans la pratique, ces dimensions sont souvent interprétées comme des genres, des styles et d'autres attributs qui s'appliquent simultanément aux utilisateurs et aux éléments. La similitude entre l'utilisateur et l'élément et, par conséquent, la note peuvent être définis comme le produit des vecteurs correspondants:

Étant donné que chaque note peut être décomposée en un produit de deux vecteurs qui appartiennent à un espace conceptuel qui n'est pas directement observé dans la matrice de notation d'origine, p et q sont appelés facteurs cachés. Le succès de cette approche abstraite dépend bien entendu entièrement de la manière dont les facteurs cachés sont déterminés et construits. Pour répondre à cette question, nous notons que l'expression 5.92 peut être réécrite sous forme matricielle comme suit:
où P est la matrice n × k assemblée à partir des vecteurs p, et Q est la matrice m × k assemblée à partir des vecteurs q, comme le montre la Fig. 5.13. L'objectif principal d'un système de filtrage conjoint est généralement de minimiser les erreurs de prédiction de la note, ce qui vous permet de déterminer directement le problème d'optimisation par rapport à la matrice des facteurs cachés:
En supposant que le nombre de dimensions cachées k est fixe et k ≤ n et k ≤ m, le problème d'optimisation 5.94 se réduit au problème d'approximation de bas rang, que nous avons considéré au chapitre 2. Pour démontrer l'approche de la solution, supposons un instant que la matrice de notation est complète. Dans ce cas, le problème d'optimisation a une solution analytique en termes de décomposition en valeurs singulières (SVD) de la matrice de notation. En particulier, en utilisant l'algorithme SVD standard, la matrice peut être décomposée en le produit de trois matrices:
où U est la matrice n × n orthonormalisée par des colonnes, Σ est la matrice diagonale n × m et V est la matrice m × m orthonormalisée par des colonnes. Une solution optimale au problème 5.94 peut être obtenue en fonction de ces facteurs, tronqués aux k dimensions les plus significatives:
Par conséquent, des facteurs cachés qui sont optimaux en termes de précision de prédiction peuvent être obtenus par décomposition singulière, comme indiqué ci-dessous:
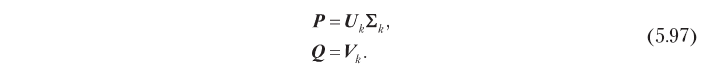
Ce modèle de facteur caché basé sur SVD aide à résoudre les problèmes de co-filtrage décrits au début de cette section. Premièrement, il remplace une grande matrice d'évaluation n × m par des matrices n × k et m × k, qui sont généralement beaucoup plus petites, car en pratique le nombre optimal de dimensions cachées k est souvent petit. Par exemple, il y a un cas où la matrice de notation avec 500 000 utilisateurs et 17 000 éléments a pu être assez bien approximée à l'aide de 40 mesures [Funk, 2016]. De plus, SVD élimine la corrélation dans la matrice de notation: les matrices de facteurs latents définies par 5.97 sont orthonormées dans les colonnes, c'est-à-dire que les dimensions cachées ne sont pas corrélées. Si, ce qui est généralement vrai dans la pratique, SVD résout également le problème de rareté, car le signal présent dans la matrice de notation initiale est effectivement concentré (rappelons que nous sélectionnons k dimensions avec l'énergie de signal la plus élevée), et les matrices de facteurs latents ne sont pas rares. La figure 5.14 illustre cette propriété. L'algorithme de proximité basé sur l'utilisateur (5.14, a) réduit les vecteurs de notation clairsemés pour un élément donné et un utilisateur donné pour obtenir un score de notation. Le modèle à facteurs cachés (5.14, b), au contraire, estime la cotation par convolution de deux vecteurs de dimension réduite et de densité énergétique plus élevée.

L'approche qui vient d'être décrite ressemble à une solution cohérente au problème des facteurs cachés, mais en fait elle présente un sérieux inconvénient en raison de l'hypothèse que la matrice de notation est complète. Si la matrice de notation est clairsemée, ce qui est presque toujours le cas, l'algorithme SVD standard ne peut pas être appliqué directement, car il ne peut pas traiter les éléments manquants (non définis). La solution la plus simple dans ce cas est de remplir les notes manquantes avec une valeur par défaut, mais cela peut conduire à un sérieux biais dans les prévisions. De plus, il est inefficace sur le plan informatique car la complexité de calcul d'une telle solution est égale à la complexité SVD pour la matrice n × m complète, alors qu'il est souhaitable d'avoir une méthode de complexité proportionnelle au nombre de notations connues. Ces problèmes peuvent être résolus à l'aide des méthodes de décomposition alternatives décrites dans les sections suivantes.
5.8.3.1. Décomposition illimitée
L'algorithme SVD standard est une solution analytique au problème d'approximation de bas rang. Cependant, ce problème peut être considéré comme un problème d'optimisation et des méthodes d'optimisation universelles peuvent également lui être appliquées. L'une des approches les plus simples consiste à utiliser la méthode de descente en gradient pour affiner de manière itérative les valeurs des facteurs cachés. Le point de départ est la définition de la fonction de coût J comme erreur de prévision résiduelle:
Veuillez noter que cette fois, nous n'imposons aucune restriction, telle que l'orthogonalité, à la matrice des facteurs cachés. En calculant le gradient de la fonction de coût par rapport aux facteurs cachés, on obtient le résultat suivant:
où E est la matrice d'erreur résiduelle:
L'algorithme de descente de gradient minimise la fonction de coût en se déplaçant à chaque étape dans la direction négative du gradient. Par conséquent, vous pouvez trouver des facteurs cachés qui minimisent l'erreur quadratique de prédiction de notation en modifiant de manière itérative les matrices P et Q pour qu'elles convergent, conformément aux expressions suivantes:

où α est la vitesse d'apprentissage. L'inconvénient de la méthode de descente de gradient est la nécessité de calculer la matrice entière des erreurs résiduelles et de changer simultanément toutes les valeurs des facteurs cachés à chaque itération. Une approche alternative, qui peut être mieux adaptée aux grandes matrices, est la descente de gradient stochastique [Funk, 2016]. L'algorithme de descente de gradient stochastique utilise le fait que l'erreur de prévision totale J est la somme des erreurs pour les éléments individuels de la matrice de notation; par conséquent, le gradient général J peut être approximé par un gradient à un point de données et les facteurs cachés peuvent être modifiés élément par élément. L'implémentation complète de cette idée est montrée dans l'algorithme 5.1.

La première étape de l'algorithme est l'initialisation de la matrice des facteurs cachés. Le choix de ces valeurs initiales n'est pas très important, mais dans ce cas, une distribution uniforme de l'énergie des notations connues parmi les facteurs cachés générés aléatoirement est choisie. Ensuite, l'algorithme optimise séquentiellement les dimensions du concept. Pour chaque mesure, il parcourt de manière répétée toutes les notes de l'ensemble d'apprentissage, prédit chaque note en utilisant les valeurs actuelles des facteurs cachés, estime l'erreur et corrige les valeurs des facteurs conformément aux expressions 5.101. L'optimisation de mesure est terminée lorsque la condition de convergence est remplie, après quoi l'algorithme passe à la mesure suivante.
L'algorithme 5.1 aide à surmonter les limites de la méthode SVD standard. Il optimise les facteurs cachés en parcourant les points de données individuels et évite ainsi les problèmes de notes manquantes et les opérations algébriques avec des matrices géantes. L'approche itérative rend également la descente de gradient stochastique plus pratique pour les applications pratiques que la descente de gradient, qui modifie des matrices entières à l'aide des expressions 5.101.
EXEMPLE 5.6
En fait, une approche basée sur des facteurs cachés est un ensemble de méthodes d'enseignement des représentations qui peuvent identifier des modèles implicites dans la matrice de notation et les représenter explicitement sous forme de concepts. Parfois, les concepts ont une interprétation complètement significative, en particulier ceux à haute énergie, bien que cela ne signifie pas que tous les concepts ont toujours une signification significative. Par exemple, l'application de l'algorithme de décomposition matricielle à une base de données de notes de films peut créer des facteurs qui correspondent approximativement à des dimensions psychographiques, telles que le mélodrame, la comédie, l'horreur, etc. Illustrons ce phénomène avec un petit exemple numérique qui utilise la matrice de notation du tableau. 5.3:

Tout d'abord, soustrayez la moyenne globale μ = 2,82 de tous les éléments pour centrer la matrice, puis exécutez l'algorithme 5.1 avec k = 3 mesures cachées et le taux d'apprentissage α = 0,01 pour obtenir les deux matrices de facteurs suivantes:

Chaque ligne de ces matrices correspond à un utilisateur ou à un film, et les 12 vecteurs de ligne sont représentés sur la Fig. 5.15. Veuillez noter que les éléments de la première colonne (le premier vecteur de concepts) ont les valeurs les plus élevées et que les valeurs des colonnes suivantes diminuent progressivement. Cela s'explique par le fait que le premier vecteur conceptuel capture autant d'énergie de signal qu'il est possible de capturer avec une mesure, le deuxième vecteur conceptuel ne capture qu'une partie de l'énergie résiduelle, etc. De plus, notez que le premier concept peut être interprété sémantiquement comme l'axe dramatique. - film d'action, où la direction positive correspond au genre du film d'action, et la négative - au genre dramatique. Les notes dans cet exemple sont fortement corrélées, il est donc clairement visible que les trois premiers utilisateurs et les trois premiers films ont de grandes valeurs négatives dans le premier vecteur conceptuel (films dramatiques et utilisateurs qui aiment ces films), tandis que les trois derniers utilisateurs et les trois derniers les films ont de grandes significations positives dans la même colonne (films d'action et utilisateurs qui préfèrent ce genre). La deuxième dimension dans ce cas particulier correspond principalement au biais de l'utilisateur ou de l'élément, qui peut être interprété comme un attribut psychographique (criticité des jugements de l'utilisateur? Popularité du film?). D'autres concepts peuvent être considérés comme du bruit.
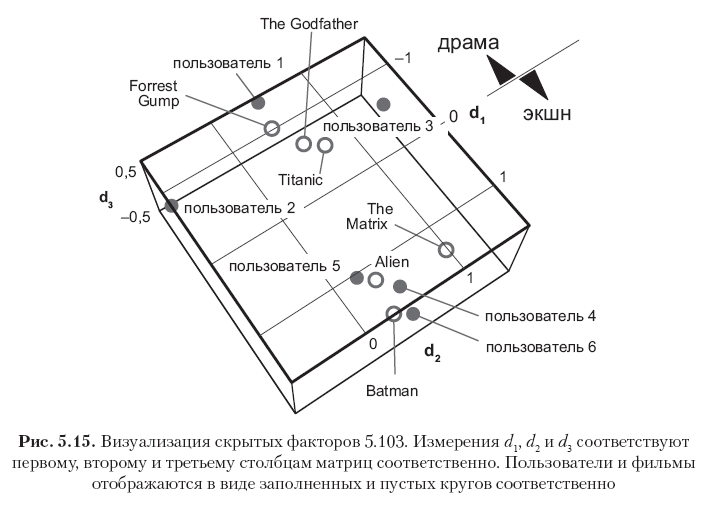
La matrice de facteurs résultante n'est pas complètement orthogonale dans les colonnes, mais a tendance à être orthogonale, car cela découle de l'optimalité de la solution SVD. Cela peut être vu en regardant les produits de PTP et QTQ, qui sont proches des matrices diagonales:
Les matrices 5.103 sont essentiellement un modèle prédictif qui peut être utilisé pour évaluer les cotes connues et manquantes. Les estimations peuvent être obtenues en multipliant deux facteurs et en ajoutant la moyenne mondiale:
Les résultats reproduisent fidèlement les notes connues et prédisent les notes manquantes conformément aux attentes intuitives. La précision des estimations peut être augmentée ou diminuée en modifiant le nombre de mesures, et le nombre optimal de mesures peut être déterminé dans la pratique en recoupant et en choisissant un compromis raisonnable entre la complexité de calcul et la précision.
»Plus d'informations sur le livre sont disponibles sur
le site Web de l'éditeur»
Contenu»
Extrait25% de réduction sur les colporteurs -
Machine LearningLors du paiement de la version papier du livre, un livre électronique est envoyé par e-mail.