Cours magistral "Fondamentaux du traitement numérique du signal"

Bonjour à tous!

Souvent, les gens se tournent vers moi avec des questions sur les tâches du domaine du traitement numérique du signal (DSP). Je raconte en détail les nuances, suggère les sources d'informations nécessaires. Mais tous les auditeurs, comme le temps l'a montré, manquent de tâches pratiques et d'exemples dans le processus d'apprentissage de ce domaine. À cet égard, j'ai décidé d'écrire un court cours interactif sur le traitement du signal numérique et de le mettre dans le domaine public .

La plupart du matériel de formation pour la présentation visuelle et interactive est mis en œuvre à l'aide du Jupyter Notebook . Il est supposé que le lecteur possède une connaissance de base du domaine des mathématiques supérieures, ainsi qu'une petite maîtrise du langage de programmation Python.

Liste des conférences

Ce cours contient du matériel sous forme de conférences terminées sur divers sujets du domaine du traitement numérique du signal. Les matériaux sont présentés à l'aide de bibliothèques Python (packages numpy, scipy, matplotlib, etc.). Les informations de base pour ce cours sont tirées de mes conférences, que j'ai, en tant qu'étudiant diplômé, donné aux étudiants de l'Institut de l'énergie de Moscou (NRU MEI). Une partie des informations de ces conférences a été utilisée lors de séminaires de formation au Center for Contemporary Electronics , où j'ai agi en tant que conférencier. En outre, ce matériel comprend la traduction de divers articles scientifiques, la compilation d'informations provenant de sources fiables et de la littérature sur le traitement numérique du signal, ainsi que la documentation officielle sur les packages d'application et les fonctions intégrées des bibliothèques scipy et numpy de Python.

Pour les utilisateurs de MATLAB (GNU Octave), la maîtrise du matériel du point de vue du code de programme n'est pas difficile, car les fonctions principales et leurs attributs sont largement identiques et similaires aux méthodes des bibliothèques Python.

Tous les matériaux sont regroupés par thèmes principaux du traitement numérique du signal:

1. Signaux: analogiques, discrets, numériques. Conversion Z
2. Transformée de Fourier: signal d'amplitude et de phase, DFT et FFT,
3. Convolution et corrélation. Convolution linéaire et cyclique. Convolution rapide
4. Processus aléatoires. Bruit blanc. Fonction de densité de probabilité
5. Signaux déterministes. Modulation: AM, FM, FM, LFM. Manipulation
6. Filtrage du signal: filtres IIR, FIR
7. Fonctions de fenêtre dans les tâches de filtrage. Détection de signaux faibles.
8. Rééchantillonnage: décimation et interpolation. Filtres CIC, filtres à moyenne mobile

La liste des conférences est suffisante mais, bien sûr, incomplète pour une initiation au domaine du DSP. Avec du temps libre, je compte soutenir et développer ce projet.

Ou trouver?

Tous les matériaux sont absolument gratuits et disponibles en tant que référentiel ouvert sur mon github en tant que projet open source . Les matériaux sont présentés sous deux formats - sous la forme de cahiers Jupyter pour le travail interactif, l'étude et l'édition, et sous la forme de fichiers HTML compilés à partir de ces cahiers (après téléchargement depuis le github, ils ont un format tout à fait approprié pour la lecture et l'impression).

Ce qui suit est une très brève description des sections du cours avec de brèves explications, termes et définitions. Les informations de base sont disponibles dans les conférences initiales, voici seulement un bref aperçu!

Signaux. Conversion Z

Section d'introduction, qui contient des informations de base sur les types de signaux. Le concept d'une séquence discrète, d'une fonction delta et d'une fonction Heaviside (saut d'unité) est introduit.

Tous les signaux selon la méthode de présentation sur le plateau peuvent être divisés en quatre groupes:

• analogique - sont décrits par des fonctions continues dans le temps,
• discrètes - sont interrompues dans le temps avec une étape spécifiée par échantillonnage,
• quantifiés - ont un ensemble de niveaux finis (généralement en amplitude),
• numérique - une combinaison des propriétés des signaux discrets et quantifiés.

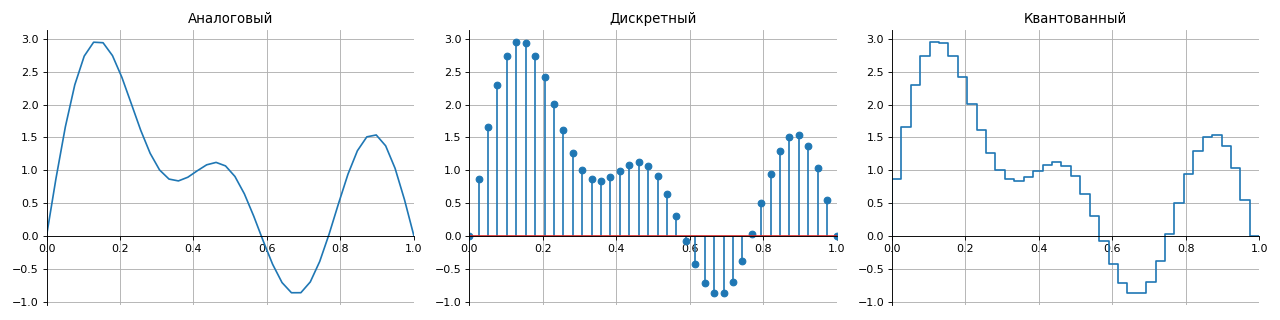
Pour la reconstruction correcte d'un signal analogique à partir d'un signal numérique sans distorsion ni perte, le théorème d'échantillonnage connu sous le nom de théorème de Kotelnikov (Nyquist-Shannon) est utilisé.

Tout signal continu avec un spectre limité peut être restauré de manière unique et sans perte à partir de ses échantillons discrets prélevés avec une fréquence strictement supérieure au double de la fréquence supérieure du spectre d'un signal continu.

Une telle interprétation est valable à condition que la fonction continue du temps occupe une bande de fréquence de 0 à la valeur de la fréquence supérieure. Si les étapes de quantification et de discrétisation sont mal choisies, le signal sera déformé de l'analogique au discret.

Dans cette section également, la transformation Z et ses propriétés sont décrites, et la représentation de séquences discrètes sous la forme Z est montrée.

Exemple d'une séquence discrète finie:

x(nT) = {2, 1, -2, 0, 2, 3, 1, 0} 

.
Un exemple de la même séquence en forme Z:

X (z) = 2 + z ^-1 - 2z ^-2 + 2z ^-4 + 3z ^-5 + 1z ^-6

Transformation de Fourier. Propriétés DFT et FFT

Cette section décrit le concept du domaine temporel et fréquentiel d'un signal. La définition de la transformée de Fourier discrète (DFT) est introduite. Les DFT directs et inverses et leurs principales propriétés sont considérés. La transition entre la DFT et l'algorithme de transformée de Fourier rapide (FFT) en base 2 (algorithmes de décimation en fréquence et en temps) est illustrée. Reflétait l'efficacité de la FFT par rapport à la DFT.

En particulier, cette section décrit le package Python scipy.ffpack pour calculer diverses transformées de Fourier (sinus, cosinus, directes, inverses, multidimensionnelles, réelles).

La transformée de Fourier vous permet de représenter n'importe quelle fonction comme un ensemble de signaux harmoniques! La transformée de Fourier est la base des méthodes de convolution et de la conception de corrélateurs numériques, est activement utilisée dans l'analyse spectrale et est utilisée lorsque l'on travaille avec des nombres longs.

Caractéristiques des spectres de signaux discrets:
1. La densité spectrale d'un signal discret est une fonction périodique avec une période égale à la fréquence d'échantillonnage.
2. Si la séquence discrète est réelle , alors le module de densité spectrale d'une telle séquence est une fonction paire , et l'argument est une fonction de fréquence impaire .

Spectre de signal harmonique:

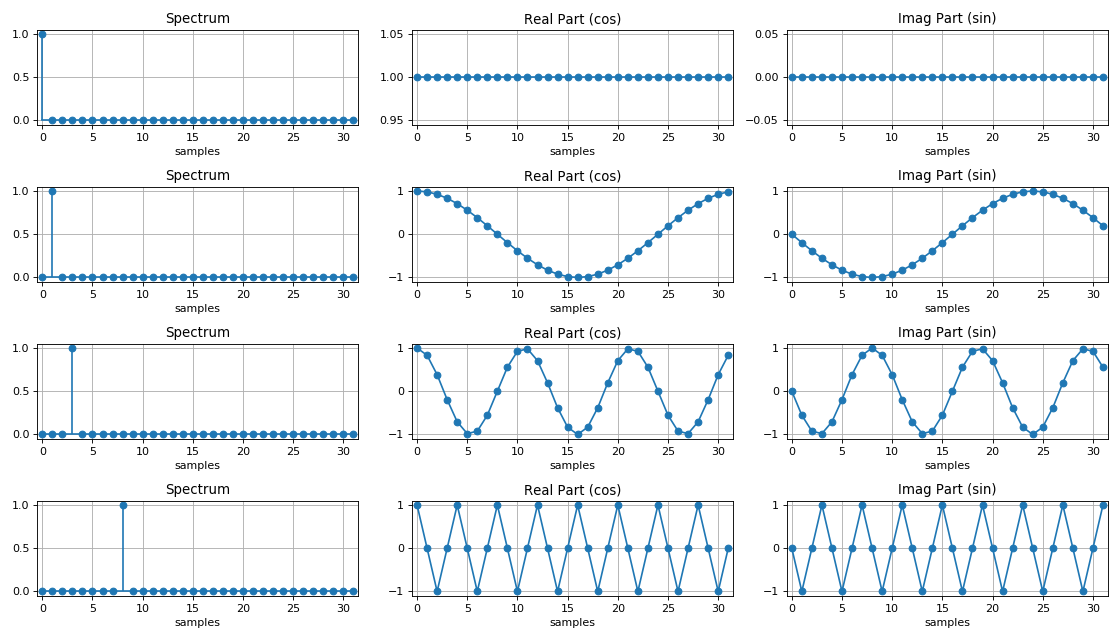
Comparaison de l'efficacité de la DFT et de la FFT

L'efficacité de l'algorithme FFT et le nombre d'opérations effectuées linéairement dépendent de la longueur de séquence N:


Comme vous pouvez le voir, plus la durée de conversion est longue, plus les économies de ressources informatiques sont importantes (en termes de vitesse de traitement ou de nombre d'unités matérielles)!

Toute forme d'onde arbitraire peut être représentée comme un ensemble de signaux harmoniques de fréquences différentes. En d'autres termes, un signal de forme complexe dans le domaine temporel a un ensemble d'échantillons complexes dans le domaine fréquentiel, qui sont appelés * harmoniques *. Ces échantillons expriment l'amplitude et la phase de l'effet harmonique à une fréquence spécifique. Plus l'ensemble des harmoniques est grand dans le domaine fréquentiel, plus la forme d'onde complexe apparaît avec précision.

Convolution et corrélation

Cette section présente le concept de corrélation et de convolution pour des séquences aléatoires et déterministes discrètes. La relation entre l'autocorrélation et les fonctions de corrélation croisée avec la convolution est présentée. Les propriétés de convolution sont décrites, en particulier, les méthodes de convolution linéaire et cyclique d'un signal discret avec une analyse détaillée sur l'exemple d'une séquence discrète sont considérées. De plus, une méthode de calcul de convolution «rapide» utilisant des algorithmes FFT est présentée.

Dans les problèmes réels, la question est souvent posée du degré de similitude d'un processus à l'autre ou de l'indépendance d'un processus par rapport à un autre. En d'autres termes, il est nécessaire de déterminer la relation entre les signaux, c'est-à-dire de trouver une corrélation . Les méthodes de corrélation sont utilisées dans un large éventail de tâches: recherche de signaux, vision par ordinateur et traitement d'images, dans les problèmes radar pour déterminer les caractéristiques des cibles et déterminer la distance à un objet. De plus, la corrélation est utilisée pour rechercher des signaux faibles dans le bruit.

La convolution décrit l'interaction des signaux entre eux. Si l'un des signaux est la réponse impulsionnelle du filtre, alors la convolution de la séquence d'entrée avec la réponse impulsionnelle n'est rien d'autre qu'une réaction du circuit à l'action d'entrée. En d'autres termes, le signal résultant reflète le passage du signal à travers le filtre.

La fonction d'autocorrélation (ACF) est utilisée pour coder les informations. Le choix de la séquence de codage en fonction des paramètres de longueur, fréquence et forme est largement dû aux propriétés de corrélation de cette séquence. La meilleure séquence de codes a la plus faible probabilité de fausse détection ou de fonctionnement (pour détecter des signaux, pour les dispositifs à seuil) ou de fausse synchronisation (pour transmettre et recevoir des séquences de code).

Cette section présente un tableau comparant l'efficacité de la convolution rapide et de la convolution calculée par la formule directe (par le nombre de multiplications réelles).

Comme vous pouvez le voir, pour des longueurs FFT jusqu'à 64, la convolution rapide perd à la méthode directe. Cependant, avec une augmentation de la longueur de la FFT, les résultats changent dans la direction opposée - une convolution rapide commence à surpasser la méthode directe. Évidemment, plus la FFT est longue, meilleur est le gain dans la méthode de fréquence.

Signaux aléatoires et bruit

Dans cette section, le concept de signaux aléatoires, densité de probabilité, loi de distribution aléatoire est introduit. Les moments mathématiques sont considérés - moyenne (attente mathématique) et variance (ou la racine de cette quantité est l'écart type). Dans cette section également, la distribution normale et le concept connexe de bruit blanc sont considérés comme la principale source de bruit (interférence) pendant le traitement du signal.

Un signal aléatoire est une fonction du temps dont les valeurs ne sont pas connues à l'avance et ne peuvent être prédites qu'avec une certaine probabilité . Les principales caractéristiques des signaux aléatoires comprennent:

• loi de distribution (temps de séjour relatif de la valeur du signal dans un certain intervalle),
• distribution spectrale de la puissance du signal.

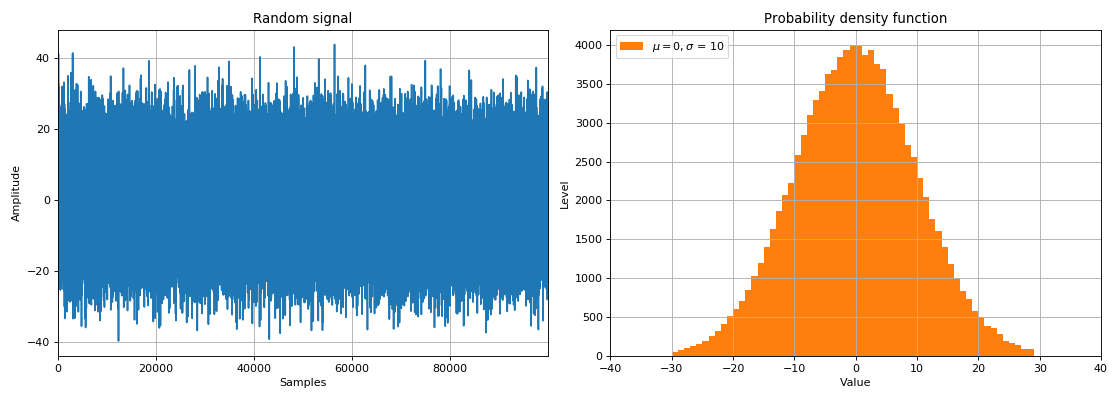
Dans les tâches DSP, les signaux aléatoires sont divisés en deux classes:

• bruit - fluctuations aléatoires consistant en un ensemble de fréquences et d'amplitudes différentes,
• signaux porteurs d'informations, pour le traitement desquels il est nécessaire de recourir à des méthodes probabilistes.

À l'aide de variables aléatoires, nous pouvons simuler l'effet d'un médium réel sur le passage d'un signal d'une source à un récepteur de données. Lorsqu'un signal passe par une liaison bruyante, le bruit dit blanc est ajouté au signal. En règle générale, la densité spectrale d'un tel bruit est uniformément (également) distribuée à toutes les fréquences, et les valeurs de bruit dans le domaine temporel sont normalement distribuées (loi de distribution gaussienne). Étant donné que le bruit blanc est physiquement ajouté aux amplitudes du signal dans les échantillons de temps sélectionnés, il est appelé bruit gaussien blanc additif (AWGN).

Signaux, modulation et manipulation

Cette section présente les méthodes de base pour modifier un ou plusieurs paramètres d'un signal harmonique. Les concepts d'amplitude, de fréquence et de modulation de phase sont introduits. En particulier, la modulation de fréquence linéaire utilisée dans les problèmes radar est mise en évidence. Les principales caractéristiques des signaux, les spectres des signaux modulés en fonction des paramètres de modulation sont représentés.



Pour plus de commodité, un ensemble de fonctions a été créé en Python qui implémente les types de modulation ci-dessus. Exemple d'implémentation d'un signal chirp:

 def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs): """ Create Chirp signal Parameters ---------- amp : float Signal magnitude beta : float Modulation bandwidth: beta < N for complex, beta < 0.5N for real freq : float or int Linear frequency of signal period : integer Number of points for signal (same as period) kwargs : bool Complex signal if is_complex = True Modulated by half-sine wave if is_modsine = True """ is_complex = kwargs.get('is_complex', False) is_modsine = kwargs.get('is_modsine', False) t = np.linspace(0, 1, period) tt = np.pi * (freq * t + beta * t ** 2) if is_complex is True: res = amp * (np.cos(tt) + 1j * np.sin(tt)) else: res = amp * np.cos(tt) if is_modsine is True: return res * np.sin(np.pi * t) return res 

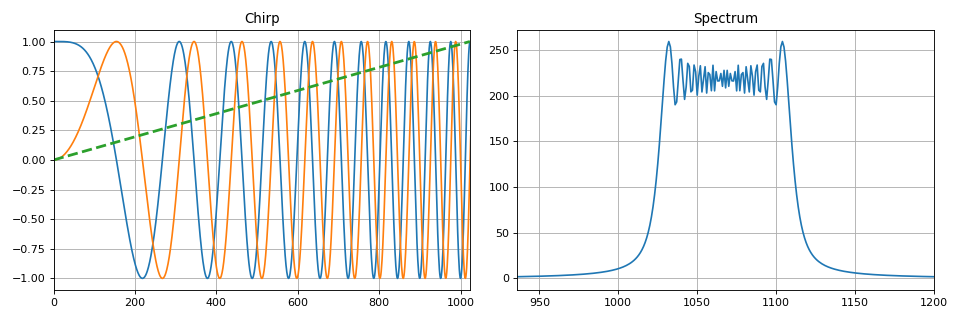
Également dans cette section de la théorie de la transmission des types de messages discrets de modulation numérique - les manipulations sont décrites. Comme dans le cas des signaux analogiques, les séquences harmoniques numériques peuvent être manipulées en amplitude, phase et fréquence (ou plusieurs paramètres à la fois).

Filtres numériques - IIR et FIR

Une section suffisamment grande consacrée au filtrage numérique des séquences discrètes. Dans les tâches de traitement du signal numérique, les données transitent par des circuits appelés filtres . Les filtres numériques, comme les filtres analogiques, ont différentes caractéristiques - fréquence: réponse en fréquence, réponse en phase, temps: réponse en impulsion, ainsi que la caractéristique de transfert du filtre. Les filtres numériques sont principalement utilisés pour améliorer la qualité du signal - pour isoler un signal d'une séquence de données ou pour dégrader des signaux indésirables - pour supprimer certains signaux dans les séquences d'échantillons entrantes.



La section répertorie les principaux avantages et inconvénients des filtres numériques (par rapport à l'analogique). Le concept des caractéristiques d'impulsion et de transfert du filtre est introduit. Deux classes de filtres sont considérées - avec une réponse impulsionnelle infinie (IIR) et une réponse impulsionnelle finie (FIR). Une méthode de conception de filtres sous forme canonique et directe est présentée. Pour les filtres FIR, la question de savoir comment passer à une forme récursive est prise en compte.



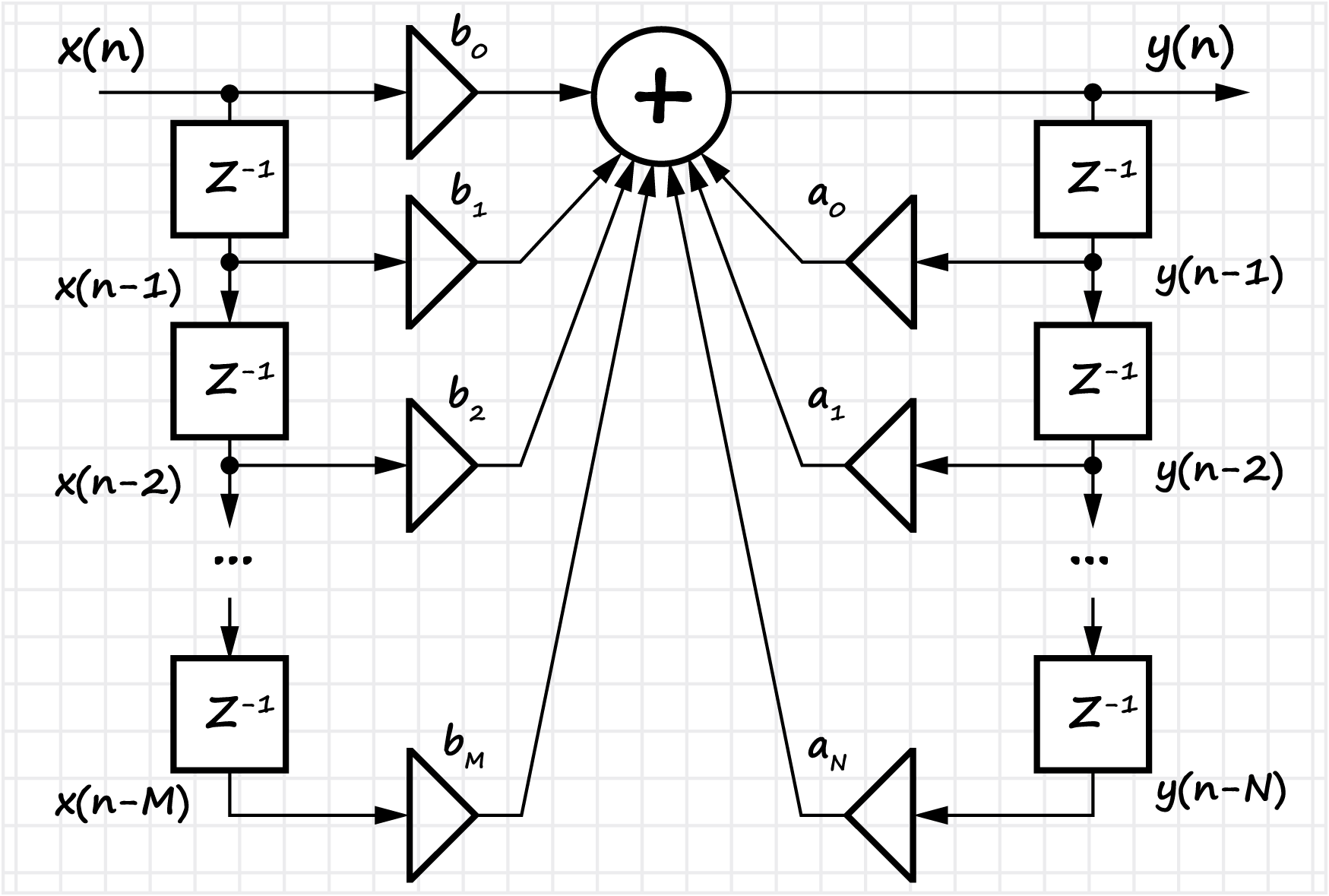
Pour les filtres FIR, le processus de conception du filtre est montré depuis le stade de développement des spécifications techniques (avec les principaux paramètres indiqués), jusqu'à la mise en œuvre logicielle et matérielle - recherche de coefficients de filtre (en tenant compte de la forme de représentation du nombre, de la profondeur de bits, etc.). Les définitions des filtres FIR symétriques, la réponse de phase linéaire et sa relation avec le concept de retard de groupe sont introduites.

Fonctions de fenêtre dans les tâches de filtrage

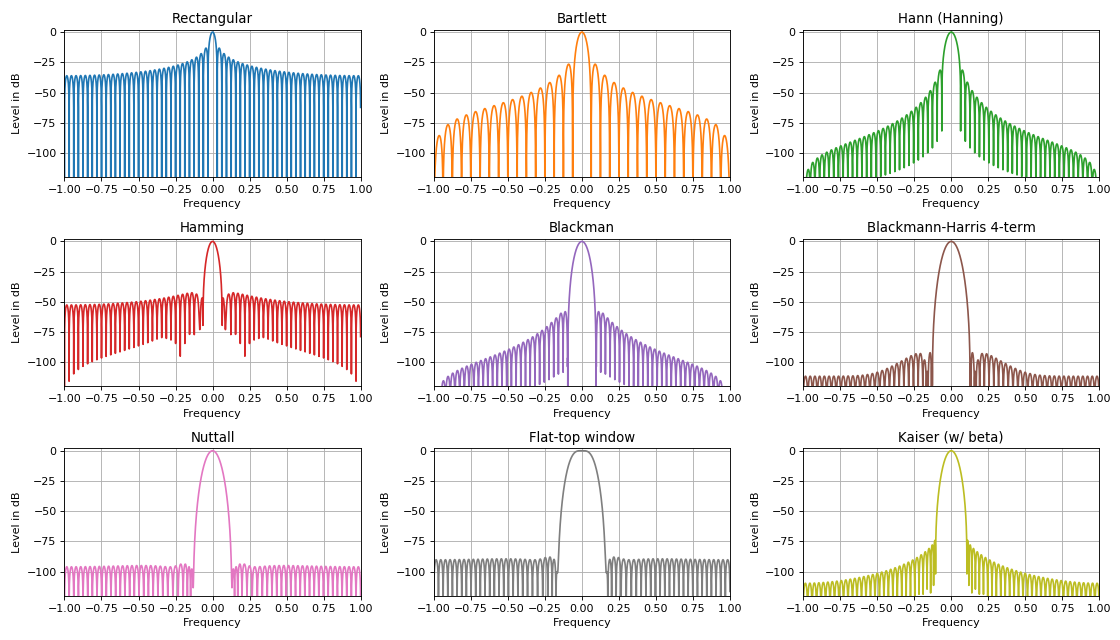
Dans les tâches de traitement numérique du signal, des fonctions de fenêtre de différentes formes sont utilisées, qui, superposées à un signal dans le domaine temporel, peuvent améliorer qualitativement ses caractéristiques spectrales. Un grand nombre de fenêtres différentes est principalement dû à l'une des principales caractéristiques de toute superposition de fenêtres. Cette caractéristique s'exprime dans la relation entre le niveau des lobes latéraux et la largeur du lobe central. Règle:

Plus la suppression des lobes latéraux du spectre est forte, plus le lobe principal du spectre est large et vice versa.

L'une des applications des fonctions de fenêtre: détection de signaux faibles sur fond de plus forts en supprimant le niveau des lobes latéraux. Les fonctions principales de la fenêtre dans les tâches DSP sont ** triangulaires, sinusoïdales, Lanczos, Hann, Hamming, Blackman, Harris, Blackman-Harris window, flat-top window, Natall, Gauss, Kaiser window ** and many others. La plupart d'entre eux sont exprimés à travers une série finie en additionnant des signaux harmoniques avec des poids spécifiques. De tels signaux sont parfaitement mis en œuvre dans la pratique sur tous les appareils matériels (circuits logiques programmables ou processeurs de signaux).

Rééchantillonnage. Décimation et interpolation

Cette section traite des problèmes du traitement du signal à plusieurs vitesses - changements dans la fréquence d'échantillonnage. Le traitement à plusieurs vitesses des signaux (traitement à plusieurs vitesses) suggère que dans le processus de conversion linéaire de signaux numériques, il est possible de changer la fréquence d'échantillonnage dans le sens de la diminution ou de l'augmentation, ou dans un nombre fractionnaire de fois. Cela conduit à un traitement du signal plus efficace, car il ouvre la possibilité d'utiliser les fréquences d'échantillonnage minimales autorisées et, par conséquent, une réduction significative des performances de calcul requises du système numérique conçu.

Décimation (décimation) - sous-échantillonnage. Interpolation - augmentation du taux d'échantillonnage.

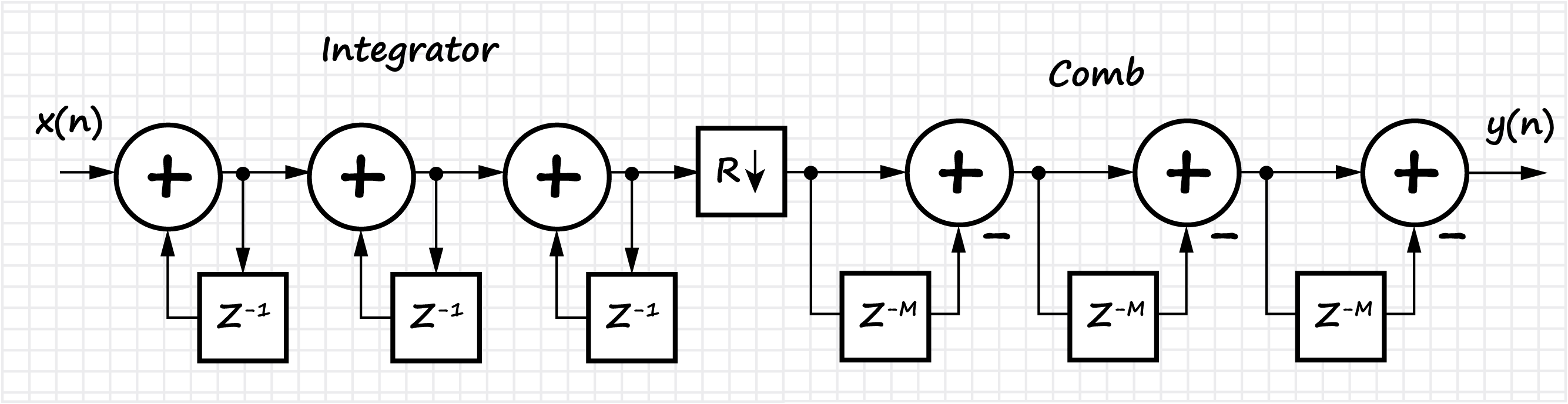
La section examine également la classe des filtres FIR homogènes, appelés filtres à peigne intégral (CIC, intégrateur en cascade - peigne). L'implémentation, les propriétés de base et les fonctionnalités des filtres CIC sont présentées. En raison de la linéarité des opérations mathématiques qui se produisent dans le filtre CIC, il est possible de mettre en cascade plusieurs filtres dans une rangée, ce qui donne une diminution proportionnelle du niveau des lobes latéraux, mais augmente également le «blocage» du lobe principal de la caractéristique amplitude-fréquence.



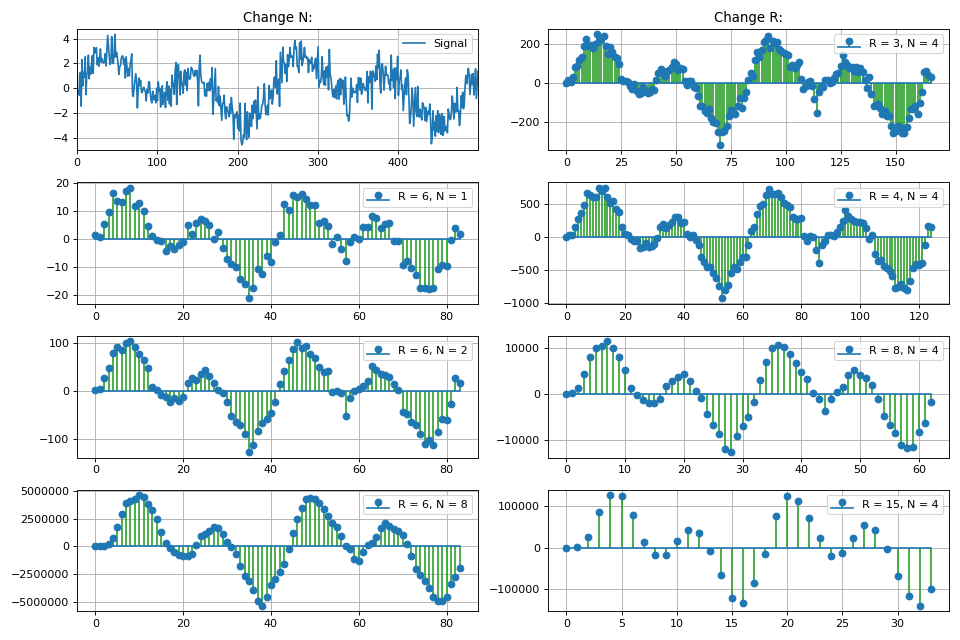
Graphique de la réponse en fréquence du filtre en fonction du coefficient de décimation:



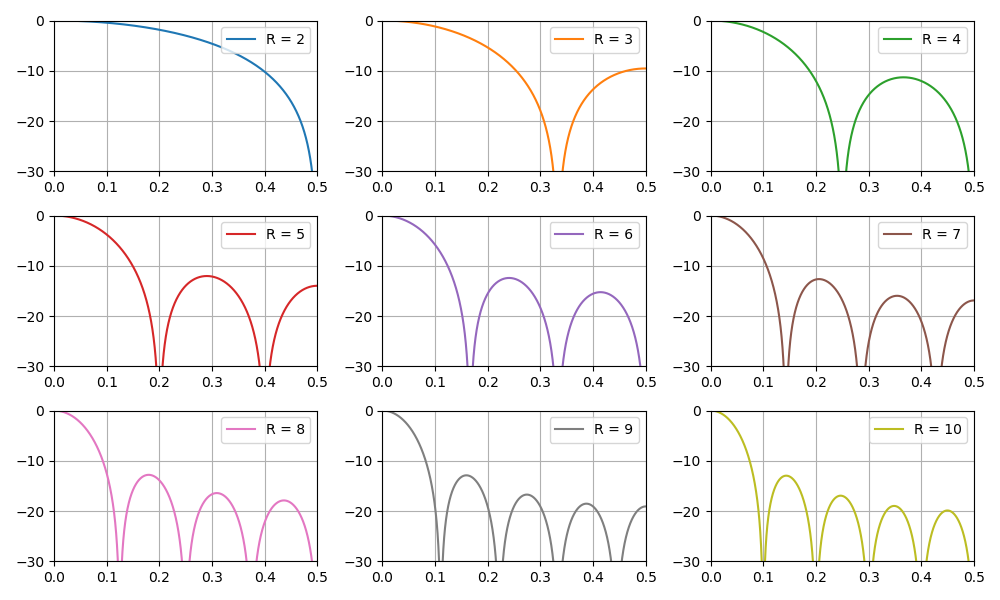
Dans cette section, nous discutons également de la question de l'augmentation de la profondeur de bits des données à la sortie du filtre CIC, en fonction de ses paramètres. Ceci est particulièrement important dans les tâches d'implémentation logicielle, en particulier sur les FPGA.

Pour l'implémentation pratique des filtres CIC en Python, une classe distincte CicFilter a été développée qui implémente des méthodes de décimation et d'interpolation. Les changements de fréquence d'échantillonnage sont également affichés à l'aide des méthodes intégrées du package scipy Python.





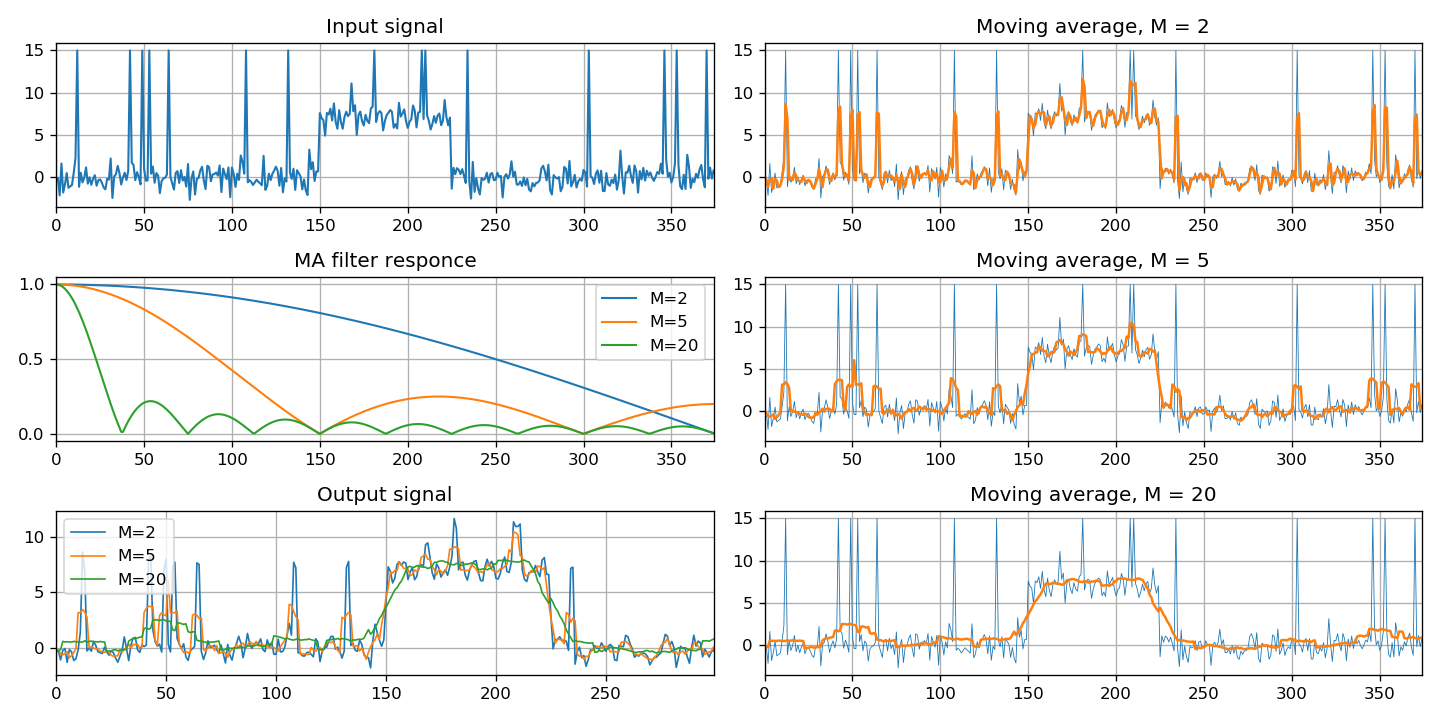
Enfin, cette section fournit une classe spéciale de filtres - la moyenne mobile. Trois méthodes de mise en œuvre sont présentées: par convolution de signaux, à l'aide d'un filtre FIR et d'un filtre IIR.

Conclusion

J'espère que ce cours en conjonction avec mes articles précédents sur le traitement numérique du signal FPGA apportera des avantages pratiques et aidera le lecteur à mieux comprendre les bases du traitement numérique du signal. Ce projet sera amélioré et complété par du nouveau matériel utile et non moins intéressant. Suivez le développement!

En plus de ce matériel, je supporte et développe mon projet sur les principaux modules DSP (en Python). Il contient un package pour générer divers signaux, une classe de filtres CIC pour les problèmes de décimation et d'interpolation, un algorithme pour calculer les coefficients d'un filtre FIR de correction, un filtre de moyenne mobile, un algorithme pour calculer une FFT ultra-longue grâce à des méthodes de conversion bidimensionnelles (ce dernier était très utile lorsque l'on travaillait avec une implémentation matérielle sur des FPGA). .

Merci de votre attention!