La traduction de l'article a été préparée pour les étudiants du cours "Mathématiques pour la science des données"

Annotation

Cet article explique la tâche de trouver les contours du visage pour une seule image. Nous montrerons comment l'ensemble d'arbres de régression peut être utilisé pour prédire la position des contours du visage directement à partir d'un sous-ensemble dispersé d'intensités de pixels, obtenant des super-performances en temps réel avec des prédictions de haute qualité. Nous présentons une structure générale basée sur l'augmentation du gradient pour étudier un ensemble d'arbres de régression qui optimise la somme des pertes quadratiques et, naturellement, traite les données manquantes ou partiellement marquées. Nous montrerons comment l'utilisation de distributions appropriées qui prennent en compte la structure des données d'image contribue à la sélection efficace des contours. Diverses stratégies de régularisation et leur importance dans la lutte contre le recyclage sont également à l'étude. De plus, nous analysons l'effet de la quantité de données d'entraînement sur la précision des prévisions et examinons l'effet de l'augmentation des données à l'aide de données synthétisées.

1. Introduction

Dans cet article, nous présentons un nouvel algorithme qui recherche les contours du visage en millisecondes et atteint une précision supérieure ou comparable aux méthodes modernes sur des ensembles de données standard. L'augmentation de la vitesse par rapport aux méthodes précédentes est une conséquence de l'identification des principaux composants des algorithmes précédents pour la recherche des contours du visage et de leur inclusion ultérieure sous une forme optimisée dans la cascade de modèles de régression à large bande passante, ajustés à l'aide de l'augmentation de gradient.

Nous démontrons, comme nous l'avons déjà fait auparavant [8, 2], que la recherche de contours du visage peut être effectuée à l'aide d'une cascade de modèles de régression. Dans notre cas, chaque modèle de régression dans la cascade prédit efficacement la forme du visage en fonction de la prévision initiale et de l'intensité de l'ensemble clairsemé de pixels indexés par rapport à cette prévision initiale. Notre travail est basé sur un grand nombre d'études menées au cours de la dernière décennie, qui ont conduit à des progrès significatifs dans la tâche de recherche des contours du visage [9, 4, 13, 7, 15, 1, 16, 18, 3, 6, 19]. En particulier, nous avons inclus dans nos modèles de régression ajustés deux éléments clés qui sont présents dans plusieurs des algorithmes réussis ci-dessous, et maintenant nous détaillons ces éléments.

Figure 1. Résultats sélectionnés sur l'ensemble de données HELEN. Pour détecter 194 points clés (repères) sur le visage dans une image en une milliseconde, un ensemble d'arbres de régression randomisés est utilisé.

Le premier tourne autour de l'indexation de l'intensité des pixels par rapport à la prévision actuelle de la forme du visage. Les caractéristiques distinctives de la représentation vectorielle de l'image du visage peuvent varier considérablement en raison de la déformation de la forme et en raison de facteurs d'interférence tels que les changements des conditions d'éclairage. Cela rend difficile la prédiction précise de la forme à l'aide de ces fonctions. Le dilemme est que nous avons besoin de signes fiables pour prédire avec précision la forme, et d'autre part, nous avons besoin d'une prévision précise de la forme pour extraire des signes fiables. Dans les travaux précédents [4, 9, 5, 8], ainsi que dans ces travaux, une approche itérative (cascade) est utilisée pour résoudre ce problème. Au lieu de régresser les paramètres de forme en fonction des entités extraites dans le système de coordonnées d'image global, l'image est convertie en un système de coordonnées normalisé en fonction de la prévision de forme actuelle, puis des signes sont extraits pour prédire le vecteur de mise à jour des paramètres de forme. Ce processus est généralement répété plusieurs fois jusqu'à la convergence.

La seconde examine comment gérer la complexité du problème d'explication / prédiction. Pendant les tests, l'algorithme de recherche de contour devrait prédire la forme du visage - un vecteur de grande dimension qui est le mieux en accord avec les données d'image et notre modèle de forme. Le problème n'est pas convexe avec de nombreux optima locaux. Des algorithmes réussis [4, 9] résolvent ce problème, en supposant que la forme prédite doit se trouver dans un sous-espace linéaire qui peut être détecté, par exemple, en trouvant les principales composantes des formes d'apprentissage. Cette hypothèse réduit considérablement le nombre de formes potentielles considérées lors de l'explication et peut aider à éviter les optima locaux.

Un travail récent [8, 11, 2] exploite le fait qu'une certaine classe de régresseurs est garantie de créer des prédictions qui se trouvent dans le sous-espace linéaire défini par les formes d'apprentissage, et il n'y a pas besoin de restrictions supplémentaires. Il est important que nos modèles de régression comportent ces deux éléments.
Ces deux facteurs sont associés à notre entraînement efficace dans le modèle de régression. Nous optimisons la fonction de perte correspondante et effectuons la sélection des fonctionnalités en fonction des données. En particulier, nous entraînons chaque régresseur en utilisant le boost de gradient [10] en utilisant la fonction de perte quadratique, la même fonction de perte que nous voulons minimiser pendant le test. L'ensemble des pixels clairsemés utilisés en entrée du régresseur est sélectionné en utilisant une combinaison de l'algorithme de renforcement de gradient et de la probabilité a priori des distances entre des paires de pixels d'entrée. Une distribution a priori permet à l'algorithme de boosting d'étudier efficacement un grand nombre de fonctionnalités pertinentes. Le résultat est une cascade de régresseurs qui peuvent localiser les repères faciaux lorsqu'ils sont initialisés par l'avant.

Les principales contributions de cet article sont:

1. Une nouvelle méthode pour trouver les contours du visage, basée sur un ensemble d'arbres de régression (arbres de décision), qui effectue la sélection des caractéristiques invariantes de la forme, tout en minimisant la même fonction de perte pendant l'entraînement que nous voulons minimiser pendant le test.
2. Nous présentons une extension naturelle de notre méthode qui traite les étiquettes manquantes ou non définies.
3. Des résultats quantitatifs et qualitatifs sont présentés, ce qui confirme que notre méthode donne des prévisions de haute qualité, étant beaucoup plus efficace que la meilleure méthode précédente (figure 1).
4. L'influence de la quantité de données de formation, de l'utilisation de données partiellement étiquetées et de données généralisées sur la qualité des prévisions est analysée.

2. Méthode

Cet article présente un algorithme pour évaluer avec précision la position des repères faciaux (points clés) en termes d'efficacité de calcul. Comme dans les travaux précédents [8, 2], la cascade de régresseurs est utilisée dans notre méthode. Dans la suite de cette section, nous décrivons les détails de la forme des composants individuels de la cascade et comment nous menons la formation.

2.1. Cascade de régression

Nous introduisons d'abord une notation. Soit , coordonnées y du i-ème point de repère du visage dans l'image I. Ensuite, le vecteur désigne les coordonnées de toutes les faces p dans I. Souvent, dans cet article, nous appelons le vecteur S une forme. Nous utilisons pour indiquer notre note actuelle S. Chaque régresseur (·, ·) Dans la cascade prédit le vecteur de mise à jour de l'image et qui est ajouté à l'évaluation actuelle du formulaire Pour améliorer la note:

) (1)

Le point clé de la cascade est que le régresseur fait ses prévisions en fonction d'attributs tels que les intensités de pixels calculées par I et indexées par rapport à l'estimation de forme actuelle . Cela introduit une sorte d'invariance géométrique dans le processus, et à mesure que vous progressez dans la cascade, vous pouvez être plus sûr que l'emplacement sémantique exact sur le visage est indexé. Nous décrirons plus tard comment cette indexation est effectuée.

Veuillez noter que la plage de sortie étendue par l'ensemble est garantie de se situer dans le sous-espace linéaire des données de formation si l'estimation initiale appartient à cet espace. Par conséquent, nous n'avons pas besoin d'introduire de restrictions supplémentaires sur les prédictions, ce qui simplifie considérablement notre méthode. La forme initiale peut simplement être sélectionnée comme la forme moyenne des données d'apprentissage, centrée et mise à l'échelle en fonction de la sortie de la boîte englobante du détecteur de visage général.

Pour éduquer tout le monde nous utilisons l'algorithme de renforcement de gradient pour les arbres avec la somme des pertes quadratiques, comme décrit dans [10]. Nous allons maintenant donner des détails détaillés sur ce processus.

2.2. Former chaque régresseur en cascade

Supposons que nous ayons des données d'entraînement où tout le monde est une image de visage, et son vecteur de forme. Pour découvrir la première fonction de régression dans la cascade, nous créons à partir de nos données d'entraînement des triplets de l'image du visage, la prévision de forme initiale et l'étape de mise à jour de la cible, c'est-à-dire ) où

(2)

(3) et

(4)

pour i = 1, ..., N.

Nous fixons le nombre total de ces triplets à N = nR, où R est le nombre d'initialisations utilisées sur l'image Ii. Chaque prévision de forme initiale pour l'image est sélectionnée uniformément dans sans remplacement.

Sur ces données, nous formons la fonction de régression (voir algorithme 1) en utilisant le renforcement du gradient des arbres avec la somme des pertes quadratiques. L'ensemble de triplets d'entraînement est ensuite mis à jour pour fournir des données d'entraînement. % 20) pour le prochain régresseur dans la cascade par réglage (avec t = 0).

% 20) (5)

(6)

Ce processus est répété jusqu'à ce qu'une cascade de régresseurs T soit formée. qui en combinaison offrent un niveau de précision suffisant.

Comme indiqué, chaque régresseur apprend en utilisant l'algorithme de renforcement d'arbre de gradient. Il convient de rappeler que la fonction de perte quadratique est utilisée et que les résidus calculés dans la boucle interne correspondent au gradient de cette fonction de perte estimé dans chaque échantillon d'apprentissage. La formulation de l'algorithme inclut le paramètre de taux d'apprentissage 0 <ν ≤ 1, également connu sous le nom de coefficient de régularisation. La définition de ν <1 aide à combattre la reconfiguration et conduit généralement à des régresseurs qui se généralisent beaucoup mieux que ceux formés avec ν = 1 [10].

Algorithme d'apprentissage 1 en cascade

Nous avons des données de formation et taux d'apprentissage (coefficient de régularisation) 0 <ν <1

1. Initialiser
   
2. pour k = 1, ..., K:
   a) nous fixons pour i = 1, ...,
   
   b) Nous ajustons l'arbre de régression à la cible avec une fonction de régression faible .
   c) Mise à jour
3. Conclusion
   

2.3. Régresseur d'arbre

Au cœur de chaque fonction de régression rt se trouvent des régresseurs arborescents adaptés aux cibles résiduelles pendant l'algorithme de renforcement de gradient. Nous allons maintenant examiner les détails d'implémentation les plus importants pour la formation de chaque arbre de régression.

2.3.1 Tests de forme fractionnée invariants

À chaque nœud de séparation dans l'arbre de régression, nous prenons une décision basée sur la valeur seuil de la différence entre les intensités de deux pixels. Les pixels utilisés dans le test sont dans les positions u et v lorsqu'ils sont définis dans le système de coordonnées de forme médiane. Pour une image d'un visage de forme arbitraire, nous voudrions indexer des points qui ont la même position par rapport à sa forme que u et v, pour la forme moyenne. Pour ce faire, avant d'extraire les éléments, l'image peut être déformée en forme médiane sur la base de l'estimation de forme actuelle. Comme nous n'utilisons qu'une représentation très clairsemée de l'image, il est beaucoup plus efficace de déformer la disposition des points que l'image entière. De plus, une approximation approximative de la déformation peut être faite en utilisant uniquement la transformation de similitude globale en plus des déplacements locaux, comme proposé dans [2].

Les détails exacts sont les suivants. Soit L'indice du repère sur le visage dans la forme médiane est-il le plus proche de u, et définit son déplacement par rapport à u comme .

Puis pour la forme Si définie dans l'image position dans , qui est qualitativement similaire à u dans l'image d'une forme moyenne, est défini comme
(7)

où et - échelle et matrice de rotation de la transformée de similitude qui transforme dans , forme moyenne.

L'échelle et la rotation minimisent

(8)

la somme des carrés entre les points de repère de la forme médiane, et point warp. définis de façon similaire.

Formellement, chaque division est une solution qui comprend 3 paramètres θ = (τ, u, v), et est appliquée à chaque exemple de formation et de test comme

(9)

où et sont déterminés en utilisant l'échelle et la matrice de rotation qui se déforment le mieux dans conformément à l'équation (7). En pratique, les tâches et les déplacements locaux sont déterminés au stade de la formation. Le calcul de la transformation de similitude, lors du test de la partie la plus coûteuse de ce processus, n'est effectué qu'une seule fois à chaque niveau de la cascade.

2.3.2 Sélection des partitions nodales

Pour chaque arbre de régression, nous approximons la fonction de base par une fonction linéaire par morceaux, où un vecteur constant convient à chaque nœud fini. Pour former l'arbre de régression, nous générons au hasard un ensemble de partitions appropriées, c'est-à-dire, θ, dans chaque nœud. Ensuite, nous sélectionnons avec empressement θ * parmi ces candidats, ce qui minimise la somme de l'erreur quadratique. Si Q est un ensemble d'indices d'exemples d'apprentissage dans un nœud, alors cela correspond à la minimisation

(10)

où - indices d'exemples envoyés au nœud gauche du fait de la décision θ, Est le vecteur de tous les résidus calculé pour l'image i dans l'algorithme de renforcement de gradient, et

pour (11)

La partition optimale peut être trouvée très efficacement, car si nous transformons l'équation (10) et omettons des facteurs indépendants de θ, nous pouvons voir que

Ici, il suffit de calculer lors de l'évaluation de divers θ, puisque peut être calculé à partir des objectifs moyens dans le nœud parent µ et comme suit:

2.3.3 Sélection des caractéristiques

La solution à chaque nœud est basée sur une valeur de seuil de la différence des valeurs d'intensité dans une paire de pixels. Il s'agit d'un test assez simple, mais il est beaucoup plus efficace qu'une valeur de seuil avec une seule intensité, en raison de sa relative insensibilité aux changements de l'éclairage global. Malheureusement, l'inconvénient d'utiliser les différences de pixels est que le nombre de candidats potentiels à la séparation (caractéristique) est quadratique par rapport au nombre de pixels dans l'image moyenne. Il est donc difficile de trouver de bons θ sans en rechercher un très grand nombre. Cependant, ce facteur limitant peut être quelque peu affaibli, compte tenu de la structure des données d'image.

Nous introduisons la distribution exponentielle

(12)

par la distance entre les pixels utilisés dans la division pour encourager la sélection de paires de pixels plus proches.

Nous avons constaté que l'utilisation de cette distribution simple réduit l'erreur de prédiction pour un certain nombre d'ensembles de données de visage. La figure 4 compare les entités sélectionnées avec et sans lui, où la taille du pool d'objets dans les deux cas est définie sur 20.

2.4. Gestion des balises manquantes

Le problème de l'équation (10) peut être facilement étendu pour traiter le cas où certains points de repère ne sont pas marqués sur certaines images d'entraînement (ou nous avons une mesure d'incertitude pour chaque point de repère). Entrez la variable [0, 1] pour chaque image d'entraînement i et chaque repère j . L'installation une valeur de 0 indique que le repère j n'est pas marqué sur la i- ième image, et un réglage de 1 indique qu'il est marqué. L'équation (10) peut alors être représentée comme suit

où - matrice diagonale avec vecteur sur sa diagonale et

pour (13)

L'algorithme d'amplification du gradient doit également être modifié pour tenir compte de ces poids. Cela peut être fait en initialisant simplement le modèle d'ensemble avec la valeur moyenne pondérée des cibles et en ajustant les arbres de régression aux résidus pondérés dans l'algorithme 1 comme suit

(14)

3. Expériences

Bases: Afin d'évaluer avec précision les performances de notre méthode proposée, ensemble d'arbres de régression (ERT), nous avons créé deux autres bases. La première est basée sur des fougères aléatoires (fougères aléatoires) avec une sélection aléatoire de traits (EF), et l'autre est une version plus avancée de cette approche avec la sélection de traits basée sur la corrélation (EF + CB), qui est notre nouvelle implémentation [2]. Tous les paramètres sont fixes pour les trois approches.

EF utilise l'implémentation directe de fougères aléatoires comme régresseurs faibles dans l'ensemble et est le plus rapide pour la formation. Nous utilisons la même méthode de régularisation que celle suggérée dans [2] pour la régularisation des fougères.

EF + CB utilise une méthode de sélection d'objets basée sur la corrélation qui projette les valeurs de sortie, , dans une direction aléatoire w et sélectionne des paires de signes (u, v) pour lesquelles a la plus forte corrélation d'échantillons pour les données d'entraînement avec les objectifs prévus .

Paramètres
, . rt T = 10, K = 500 . ( ), , F = 5. P = 400 . , P , (9). S = 20 , . , R = 20 .

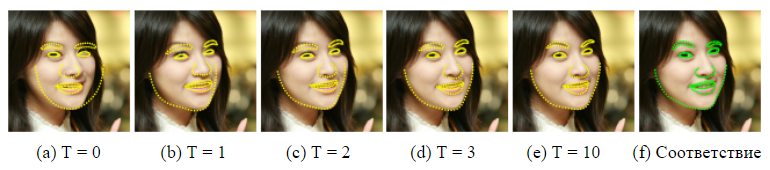
2. , Viola & Jones [17]. .

O (TKF). O (NDTKF S), N — , D — . HELEN [12], .

, , HELEN [12], , , . 2330 , 194 . 2000 , .

LFPW [1], 1432 . , 778 216 , , .

Comparaison
1 . (Active Shape Models) — STASM [14] CompASM [12].

1. HELEN. — . . , . , . .

, , . 3 , , ERT , . , EF + CB . , EF + CB , .

LFPW [1] ( 2). EF + CB , [2]. ( , .) , , .

2. LFPW. 1.

4 (12) , , . λ 0,1 . . 4 .

3. . , , . (12).

, . , . — . ν 1 ( ν = 0.1). . , , , ν = 1. (10 ) . ( .)

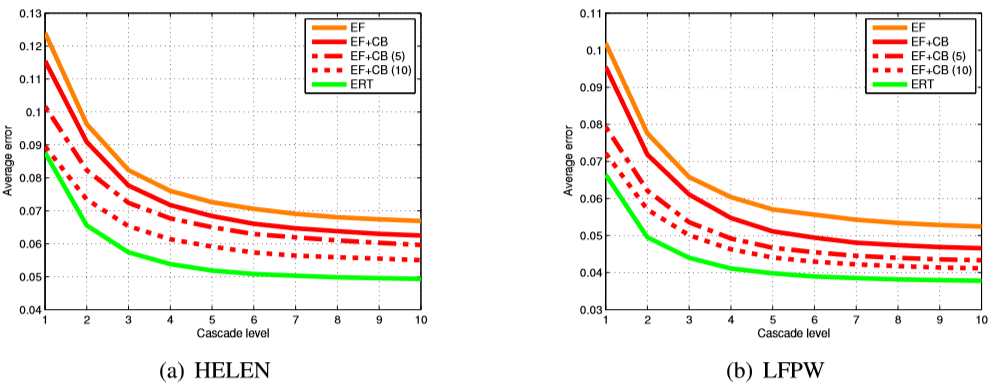
3. HELEN (a) LFPW (b). EF — , EF + CB — , . (5 10), [2]. , (ERT), , , .

4. , . , .

, . , .

4. HELEN . .

, . , , , , .

. . 5 . , , [8, 2] ( 10 × 400 .)

5. .

Données d'entraînement
Afin de tester l'efficacité de notre méthode en termes de nombre d'images d'entraînement, nous avons formé différents modèles à partir de différents sous-ensembles de données d'entraînement. Le tableau 6 résume les résultats finaux et la figure 5 montre un graphique des erreurs à chaque niveau de la cascade. L'utilisation de plusieurs niveaux de régresseurs est plus utile lorsque nous avons un grand nombre d'exemples de formation.

Nous avons répété les mêmes expériences avec un nombre total fixe d'exemples étendus, mais avons changé la combinaison des formes initiales utilisées pour créer l'exemple d'apprentissage à partir d'un exemple marqué du visage et d'un certain nombre d'images annotées utilisées pour étudier la cascade (tableau 7).

Tableau 6. Taux d'erreur final pour le nombre d'exemples de formation. Lors de la création de données d'apprentissage pour étudier les régresseurs en cascade, chaque image de visage étiqueté a généré 20 exemples d'apprentissage, en utilisant 20 visages étiquetés différents comme hypothèse initiale sur la forme du visage.

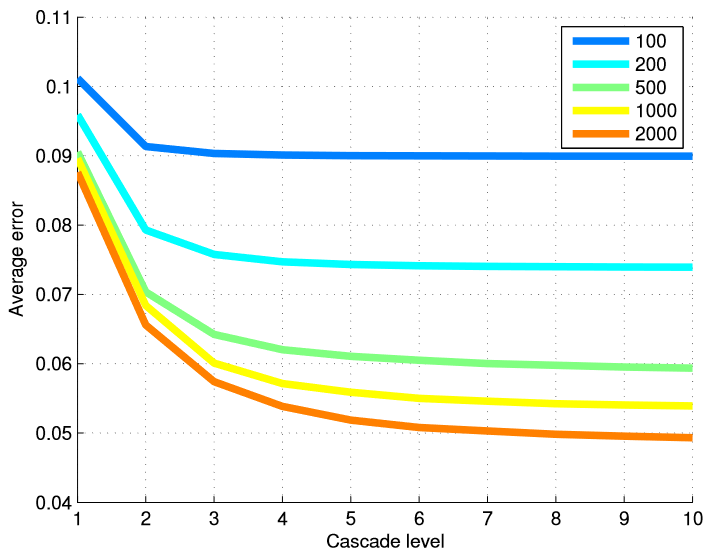
Figure 5. L'erreur moyenne à chaque niveau de la cascade est présentée en fonction du nombre d'exemples de formation utilisés. L'utilisation de plusieurs niveaux de régresseurs est particulièrement utile lorsque le nombre d'exemples de formation est important.

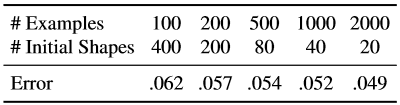
Tableau 7. Ici, le nombre effectif d'exemples d'entraînement est fixe, mais nous utilisons différentes combinaisons du nombre d'images d'entraînement et du nombre de formes initiales utilisées pour chaque image faciale marquée.

L'augmentation des données de formation à l'aide d'une variété de formulaires initiaux élargit l'ensemble de données en termes de forme. Nos résultats montrent que ce type de complément ne compense pas totalement l'absence d'images d'entraînement annotées. Bien que le taux d'amélioration obtenu en augmentant le nombre d'images d'entraînement diminue rapidement après les quelques premières centaines d'images.

Annotations partielles
Le tableau 8 montre les résultats de l'utilisation de données partiellement annotées. 200 études de cas sont entièrement annotées et les autres seulement partiellement.

Tableau 8. Résultats utilisant des données partiellement étiquetées. 200 exemples sont toujours complètement annotés. Les valeurs entre parenthèses indiquent le pourcentage de repères observés.

Les résultats montrent que nous pouvons obtenir une amélioration significative en utilisant des données partiellement étiquetées. Cependant, l'amélioration affichée peut ne pas être saturée, car nous savons que la taille de base des paramètres de forme est bien inférieure à la taille des points de repère (194 × 2). Par conséquent, il existe un potentiel d'amélioration plus significative avec les marques partielles, si vous utilisez explicitement la corrélation entre la position des points de repère. Veuillez noter que la procédure de renforcement du gradient décrite dans cet article n'utilise pas de corrélation entre les points de repère. Ce problème peut être résolu dans les travaux futurs.

4. Conclusion

Nous avons décrit comment un ensemble d'arbres de régression peut être utilisé pour régresser l'emplacement des repères faciaux à partir d'un sous-ensemble dispersé de valeurs d'intensité extraites de l'image d'entrée. La structure présentée réduit les erreurs plus rapidement que le travail précédent et peut également traiter des marques partielles ou non définies. Alors que les principales composantes de notre algorithme considèrent diverses mesures cibles comme des variables indépendantes, la poursuite naturelle de ce travail sera l'utilisation de la corrélation des paramètres de forme pour une formation plus efficace et une meilleure utilisation des étiquettes partielles.

Figure 6. Résultats finaux dans la base de données HELEN.

Remerciements
Ce travail a été financé par la Fondation suédoise de recherche stratégique dans le cadre du projet VINST.

Littérature utilisée

[1] PN Belhumeur, DW Jacobs, DJ Kriegman et N. Kumar. Localisation de parties de visages à l'aide d'un consensus d'exemplaires. Dans CVPR, pages 545–552, 2011. 1, 5
[2] X. Cao, Y. Wei, F. Wen et J. Sun. Alignement des faces par régression de forme explicite. Dans CVPR, pages 2887–2894, 2012. 1, 2, 3, 4, 5, 6
[3] TF Cootes, M. Ionita, C. Lindner et P. Sauer. Ajustement de modèle de forme robuste et précis en utilisant le vote de régression forestière aléatoire. Dans ECCV, 2012.1
[4] TF Cootes, CJ Taylor, DH Cooper et J. Graham. Modèles de forme active - leur formation et leur application. Vision par ordinateur et compréhension de l'image, 61 (1): 38–59, 1995.1, 2
[5] D. Cristinacce et TF Cootes. Modèles de forme active de régression boostée. Dans BMVC, pages 79.1–79.10, 2007.1
[6] M. Dantone, J. Gall, G. Fanelli et LV Gool. Détection des traits du visage en temps réel à l'aide de forêts de régression conditionnelle. Dans CVPR, 2012.1
[7] L. Ding et AM Mart´ınez. Détection précise et précise des visages et des traits du visage. Dans CVPR, 2008.1
[8] P. Dollar, P. Welinder et P. Perona. Régression de la pose en cascade. Dans CVPR, pages 1078–1085, 2010. 1, 2, 6
[9] GJ Edwards, TF Cootes et CJ Taylor. Progrès dans les modèles d'apparence active. Dans ICCV, pages 137–142, 1999. 1, 2
[10] T. Hastie, R. Tibshirani et JH Friedman. Les éléments de l'apprentissage statistique: exploration de données, inférence et prédiction. New York: Springer-Verlag, 2001.2,3
[11] V. Kazemi et J. Sullivan. Alignement des faces avec modélisation basée sur les pièces. Dans BMVC, pages 27.1-27.10, 2011.2
[12] V. Le, J. Brandt, Z. Lin, LD Bourdev et TS Huang. Localisation interactive des traits du visage. Dans [13] L. Liang, R. Xiao, F. Wen et J. Sun. Alignement des visages via une recherche discriminante basée sur les composants. Dans ECCV, pages 72–85, 2008. 1ECCV, pages 679– 692, 2012.5
[14] S. Milborrow et F. Nicolls. Localisation des traits du visage avec un modèle de forme actif étendu. Dans ECCV, pages 504–513, 2008.5
[15] J. Saragih, S. Lucey et J. Cohn. Ajustement du modèle déformable par des décalages moyens des points de repère régularisés. Journal international de vision par ordinateur, 91: 200–215, 2010.1
[16] BM Smith et L. Zhang. Alignement de la face du joint avec des modèles de forme non paramétriques. Dans ECCV, pages 43–56, 2012.1
[17] PA Viola et MJ Jones. Détection de visage en temps réel robuste. Dans ICCV, page 747, 2001.5
[18] X. Zhao, X. Chai et S. Shan. Alignement de la face articulaire: sauvez les mauvais alignements avec les bons par un réajustement régulier. Dans ECCV, 2012.1
[19] X. Zhu et D. Ramanan. Détection des visages, estimation des poses et localisation des repères dans la nature. Dans CVPR, pages 2879–2886, 2012.1