Pourquoi le prochain article sur la façon d'écrire des réseaux de neurones à partir de zéro? Hélas, je n'ai pas pu trouver d'articles où la théorie et le code ont été décrits de A à Z pour un modèle pleinement fonctionnel. J'avertis immédiatement qu'il y aura beaucoup de mathématiques. Je suppose que le lecteur connaît les bases de l'algèbre linéaire, les dérivées partielles et au moins partiellement la théorie des probabilités, ainsi que Python et Numpy. Nous traiterons d'un réseau neuronal entièrement connecté et du MNIST.
Math Partie 1 (simple)
Qu'est-ce qu'une couche entièrement connectée (couche FC)? Habituellement, ils disent quelque chose comme «Une couche entièrement connectée est une couche, dont chaque neurone est connecté à tous les neurones de la couche précédente». Ce n'est tout simplement pas clair ce que sont les neurones, comment ils sont connectés, en particulier dans le code. Maintenant, je vais essayer d'analyser cela avec un exemple. Soit une couche de 100 neurones. Je sais que je n'ai pas encore expliqué de quoi il s'agit, mais imaginons simplement qu'il y a 100 neurones et qu'ils ont une entrée d'où les données sont envoyées et une sortie d'où ils donnent les données. Et une image en noir et blanc de 28x28 pixels est envoyée à l'entrée - seulement 784 valeurs, si vous l'étirez en un vecteur. Une image peut être appelée couche d'entrée. Ensuite, pour que chacun des 100 neurones se connecte avec chaque "neurone" ou, si vous le souhaitez, la valeur de la couche précédente (c'est-à-dire l'image), il est nécessaire que chacun des 100 neurones accepte 784 valeurs de l'image d'origine. Par exemple, pour chacun des 100 neurones, il suffira de multiplier 784 valeurs de l'image par quelques 784 nombres et de les additionner, par conséquent, un nombre sort. Autrement dit, ceci est un neurone:
$$ afficher $$ \ text {sortie Neuron} = \ text {un certain nombre} _ {1} \ cdot \ text {valeur d'image} _1 ~ + \\ + ~ ... ~ + ~ \ text {some- ce nombre} _ {784} \ cdot \ text {valeur d'image} _ {784} $$ display $$
Ensuite, il s'avère que chaque neurone a 784 nombres, et tous ces nombres: (nombre de neurones sur cette couche) x (nombre de neurones sur la couche précédente) =
$ en ligne $ 100 \ times784 $ en ligne $ = 78 400 chiffres. Ces nombres sont communément appelés poids des couches. Chaque neurone donnera son numéro et par conséquent nous obtenons un vecteur à 100 dimensions, et en fait, nous pouvons écrire que ce vecteur à 100 dimensions est obtenu en multipliant le vecteur à 784 dimensions (notre image originale) par une matrice de poids de taille
$ en ligne $ 100 \ times784 $ en ligne $ :
$$ afficher $$ \ boldsymbol {x} ^ {100} = W_ {100 \ times784} \ cdot \ boldsymbol {x} ^ {784} $$ afficher $$
De plus, les 100 nombres résultants sont transmis à la fonction d'activation - une fonction non linéaire - qui affecte chaque nombre séparément. Par exemple, sigmoïde, tangente hyperbolique, ReLU et autres. La fonction d'activation est nécessairement non linéaire, sinon le réseau neuronal n'apprendra que des transformations simples.
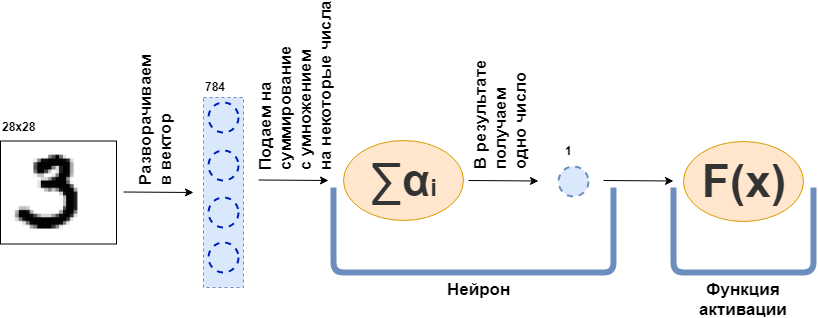
Ensuite, les données résultantes sont à nouveau transmises à une couche entièrement connectée, mais avec un nombre différent de neurones, et à nouveau à la fonction d'activation. Cela se produit plusieurs fois. La dernière couche du réseau est la couche qui produit la réponse. Dans ce cas, la réponse est une information sur le numéro dans l'image.
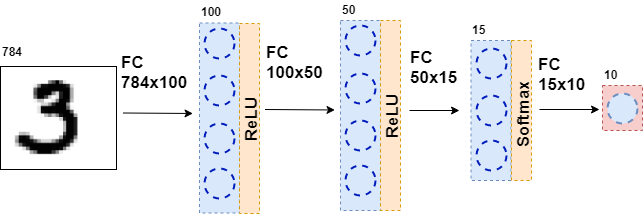
Lors de la formation du réseau, il est nécessaire que nous sachions quelle figure est montrée sur l'image. Autrement dit, l'ensemble de données est balisé. Ensuite, vous pouvez utiliser un autre élément - la fonction d'erreur. Elle regarde la réponse du réseau neuronal et la compare à la vraie réponse. Grâce à cela, le réseau neuronal apprend.
Énoncé général du problème
L'ensemble de données est un grand tenseur (nous appellerons un tableau de données multidimensionnel un tenseur)
$ inline $ \ boldsymbol {X} = \ left [\ boldsymbol {x} _1, \ boldsymbol {x} _2, \ ldots, \ boldsymbol {x} _n \ right] $ inline $ où
$ inline $ \ boldsymbol {x} _i $ inline $ - i-ème objet, par exemple, une image, qui est aussi un tenseur. Pour chaque objet il y a
$ inline $ y_i $ inline $ - la bonne réponse sur le i-ème objet. Dans ce cas, un réseau neuronal peut être représenté comme une fonction qui prend un objet en entrée et donne une réponse à ce sujet:
$$ afficher $$ F (\ boldsymbol {x} _i) = \ chapeau {y} _i $$ afficher $$
Examinons maintenant de plus près la fonction
$ inline $ F (\ boldsymbol {x} _i) $ inline $ . Puisque le réseau neuronal est constitué de couches, chaque couche individuelle est une fonction. Et cela signifie
$$ afficher $$ F (\ boldsymbol {x} _i) = f_k (f_ {k-1} (\ ldots (f_1 (\ boldsymbol {x} _i)))) = \ hat {y} _i $$ afficher $ $
Autrement dit, dans la toute première fonction - la première couche - une image est présentée sous la forme d'un tenseur. Fonction
$ inline $ f_1 $ inline $ donne une réponse - aussi un tenseur, mais d'une dimension différente. Ce tenseur sera appelé la représentation interne. Maintenant, cette représentation interne est alimentée à l'entrée de la fonction
$ inline $ f_2 $ inline $ , qui donne sa représentation interne. Et ainsi de suite, jusqu'à ce que la fonction
$ inline $ f_k $ inline $ - dernière couche - ne donnera pas de réponse
$ inline $ \ hat {y} _i $ inline $ .
Maintenant, la tâche est de former le réseau - pour que la réponse du réseau corresponde à la bonne réponse. Vous devez d'abord mesurer à quel point le réseau de neurones est incorrect. Mesurer cela est une fonction d'erreur.
$ inline $ L (\ hat {y} _i, y_i) $ inline $ . Et nous imposons des restrictions:
1.
$ inline $ \ hat {y} _i \ xrightarrow {} y_i \ Rightarrow L (\ hat {y} _i, y_i) \ xrightarrow {} 0 $ inline $
2.
$ inline $ \ existe ~ dL (\ hat {y} _i, y_i) $ inline $
3.
$ inline $ L (\ hat {y} _i, y_i) \ geq 0 $ inline $
La restriction 2 est imposée sur toutes les fonctions des couches
$ inline $ f_j $ inline $ - qu'ils soient tous différenciables.
De plus, en fait (je n'ai pas mentionné cela) certaines de ces fonctions dépendent des paramètres - les poids du réseau neuronal -
$ inline $ f_j (\ boldsymbol {x} _i | \ boldsymbol {\ omega} _j) $ inline $ . Et l'idée est de prendre de tels poids pour que
$ inline $ \ hat {y} _i $ inline $ coïncidé avec
$ inline $ y_i $ inline $ sur tous les objets d'un jeu de données. Je note que toutes les fonctions n'ont pas de poids.
Alors, où en sommes-nous? Toutes les fonctions du réseau neuronal sont différenciables, la fonction d'erreur est également différenciable. Rappelez-vous l'une des propriétés du gradient - montrer la direction de croissance de la fonction. Nous utilisons cela, les restrictions 1 et 3, le fait que
$$ affiche $$ L (F (\ boldsymbol {x} _i)) = L (f_k (f_ {k-1} (\ ldots (f_1 (\ boldsymbol {x} _i))))))) = L (\ hat {y} _i) $$ afficher $$
et le fait que je puisse considérer les dérivées partielles et les dérivées d'une fonction complexe. Maintenant, il y a tout ce dont vous avez besoin pour calculer
$$ afficher $$ \ frac {\ partiel L (F (\ boldsymbol {x} _i))} {\ partiel \ boldsymbol {\ omega_j}} $$ afficher $$
pour tout i et j. Cette dérivée partielle montre la direction dans laquelle changer
$ inline $ \ boldsymbol {\ omega_j} $ inline $ agrandir
$ en ligne $ L $ en ligne $ . Pour réduire, vous devez faire un pas de côté
$ inline $ - \ frac {\ partial L (F (\ boldsymbol {x} _i))} {\ partial \ boldsymbol {\ omega_j}} $ inline $ rien de compliqué.
Ainsi, le processus de formation du réseau est construit comme suit: plusieurs fois dans un cycle, nous parcourons l'ensemble de données (c'est ce qu'on appelle une ère), pour chaque objet de l'ensemble de données que nous considérons
$ inline $ L (\ hat {y} _i, y_i) $ inline $ (c'est ce que l'on appelle la passe avant) et considérons la dérivée partielle
$ inline $ \ partiel L $ inline $ pour tous les poids
$ inline $ \ boldsymbol {\ omega_j} $ inline $ , puis mettez à jour les poids (c'est ce que l'on appelle le passage en arrière).
Je note que je n'ai pas encore introduit de fonctions et de couches spécifiques. Si à ce stade, on ne sait pas quoi faire de tout cela, je propose de continuer à lire - il y aura plus de mathématiques, mais maintenant il ira avec des exemples.
Math Partie 2 (difficile)
Fonction d'erreur
Je vais commencer par la fin et dériver la fonction d'erreur pour le problème de classification. Pour le problème de régression, la dérivation de la fonction d'erreur est bien décrite dans le livre «Deep Learning. Immersion dans le monde des réseaux de neurones. "
Pour simplifier, il existe un réseau de neurones (NN) qui sépare les photos de chats des photos de chiens, et il existe un ensemble de photos de chats et de chiens pour lesquelles il existe une bonne réponse.
$ inline $ y_ {true} $ inline $ .
$$ afficher $$ NN (image | \ Omega) = y_ {pred} $$ afficher $$
Tout ce que je vais faire ensuite est très similaire à la méthode du maximum de vraisemblance. Par conséquent, la tâche principale consiste à trouver la fonction de vraisemblance. Si nous omettons les détails, alors une telle fonction qui compare la prédiction du réseau neuronal et la bonne réponse, et si elles coïncident, donne une grande valeur, sinon, vice versa. La probabilité d'une réponse correcte vient à l'esprit avec les paramètres donnés:
$$ afficher $$ p (y_ {pred} = y_ {vrai} | \ Omega) $$ afficher $$
Et maintenant, nous allons faire une feinte, qui, semble-t-il, ne suit nulle part. Que le réseau neuronal donne une réponse sous la forme d'un vecteur bidimensionnel dont la somme des valeurs est 1. Le premier élément de ce vecteur peut être appelé une mesure de confiance que le chat est sur la photo et le deuxième élément la mesure de confiance que le chien est sur la photo. Oui, c'est presque une probabilité!
$$ afficher $$ NN (image | \ Omega) = \ gauche [\ commencer {matrice} p_0 \\ p_1 \\\ fin {matrice} \ droite] $$ afficher $$
Maintenant, la fonction de vraisemblance peut être réécrite comme suit:
$$ affiche $$ p (y_ {pred} = y_ {true} | \ Omega) = p_ \ Omega (y_ {pred}) ^ t_ {0} * (1 - p_ \ Omega (y_ {pred})) ^ t_ {1} = \\ p_0 ^ {t_0} * p_1 ^ {t_1} $$ afficher $$
O Where
$ inline $ t_0, t_1 $ inline $ les étiquettes de la bonne classe, par exemple, si
$ inline $ y_ {true} = cat $ inline $ alors
$ inline $ t_0 == 1, t_1 == 0 $ inline $ si
$ inline $ y_ {true} = chien $ inline $ alors
$ inline $ t_0 == 0, t_1 == 1 $ inline $ . Ainsi, la probabilité d'une classe qui aurait dû être prédite par un réseau de neurones (mais pas nécessairement prédite par lui) est toujours considérée. Maintenant, cela peut être généralisé à n'importe quel nombre de classes (par exemple, m classes):
$$ afficher $$ p (y_ {pred} = y_ {vrai} | \ Omega) = \ prod_0 ^ m p_i ^ {t_i} $$ afficher $$
Cependant, dans tout jeu de données, il existe de nombreux objets (par exemple, N objets). Je veux que le réseau neuronal donne la bonne réponse sur chacun ou la plupart des objets. Et pour cela, vous devez multiplier les résultats de la formule ci-dessus pour chaque objet de l'ensemble de données.
$$ afficher $$ MaximumL vraisemblance = \ prod_ {j = 0} ^ N \ prod_ {i = 0} ^ m p_ {i, j} ^ {t_ {i, j}} $$ afficher $$
Pour obtenir de bons résultats, cette fonction doit être maximisée. Mais, premièrement, il est plus raide à minimiser, car nous avons une descente de gradient stochastique et tous les petits pains pour cela - attribuez simplement un moins, et deuxièmement, il est difficile de travailler avec un travail énorme - c'est le logarithme.
$$ afficher $$ CrossEntropyLoss = - \ sum \ limits_ {j = 0} ^ {N} \ sum \ limits_ {i = 0} ^ {m} t_ {i, j} \ cdot \ log (p_ {i, j }) $$ afficher $$
Super! Le résultat était une entropie croisée ou, dans le cas binaire, une perte de log. Cette fonction est facile à compter et encore plus facile à différencier:
$$ display $$ \ frac {\ partial CrossEntropyLoss} {\ partial p_j} = - \ frac {\ boldsymbol {t_j}} {\ boldsymbol {p_ {j}}} $$ display $$
Vous devez différencier l'algorithme de rétropropagation. Je note que la fonction d'erreur ne change pas la dimension du vecteur. Si, comme dans le cas de MNIST, la sortie est un vecteur de réponses à 10 dimensions, alors lors du calcul de la dérivée, nous obtenons un vecteur à 10 dimensions de dérivées. Une autre chose intéressante est qu'un seul élément de la dérivée ne sera pas nul, auquel
$ inline $ t_ {i, j} \ neq 0 $ inline $ , c'est-à-dire avec la bonne réponse. Et moins la probabilité d'une réponse correcte est prédite par un réseau de neurones sur un objet donné, plus la fonction d'erreur y sera.
Fonctionnalités d'activation
À la sortie de chaque couche entièrement connectée d'un réseau de neurones, une fonction d'activation non linéaire doit être présente. Sans lui, il est impossible de former un réseau neuronal significatif. Pour l'avenir, une couche entièrement connectée d'un réseau de neurones est simplement une multiplication des données d'entrée par une matrice de poids. En algèbre linéaire, cela s'appelle une carte linéaire - une fonction linéaire. La combinaison de fonctions linéaires est également une fonction linéaire. Mais cela signifie qu'une telle fonction ne peut qu'approcher des fonctions linéaires. Hélas, ce n'est pas pourquoi des réseaux de neurones sont nécessaires.
Softmax
Habituellement, cette fonction est utilisée sur la dernière couche du réseau, car elle transforme le vecteur de la dernière couche en un vecteur de «probabilités»: chaque élément du vecteur se situe de 0 à 1 et leur somme est 1. Elle ne change pas la dimension du vecteur.
$$ afficher $$ Softmax_i = \ frac {e ^ {x_i}} {\ sum \ limits_ {j} e ^ {x_j}} $$ afficher $$
Passons maintenant à la recherche dérivée. Depuis
$ inline $ \ boldsymbol {x} $ inline $ Est un vecteur, et tous ses éléments sont toujours présents dans le dénominateur, puis en prenant la dérivée on obtient le jacobien:
$$ display $$ J_ {Softmax} = \ begin {cases} x_i - x_i \ cdot x_j, i = j \\ - x_i \ cdot x_j, i \ neq j \ end {cases} $$ display $$
Maintenant sur la rétropropagation. Le vecteur des dérivés provient de la couche précédente (il s'agit généralement d'une fonction d'erreur)
$ inline $ \ boldsymbol {dz} $ inline $ . Au cas où
$ inline $ \ boldsymbol {dz} $ inline $ provenait d'une fonction d'erreur sur mnist,
$ inline $ \ boldsymbol {dz} $ inline $ - Vecteur à 10 dimensions. Ensuite, le jacobien a une dimension de 10x10. Pour obtenir
$ inline $ \ boldsymbol {dz_ {new}} $ inline $ , qui va plus loin dans la couche précédente (n'oubliez pas que l'on va de la fin au début du réseau quand l'erreur se propage), il faut multiplier
$ inline $ \ boldsymbol {dz} $ inline $ sur
$ inline $ J_ {Softmax} $ inline $ (ligne par colonne):
$$ afficher $$ dz_ {nouveau} = \ boldsymbol {dz} \ fois J_ {Softmax} $$ afficher $$
En sortie, nous obtenons un vecteur à 10 dimensions de dérivées
$ inline $ \ boldsymbol {dz_ {new}} $ inline $ .
Relu
$$ display $$ ReLU (x) = \ begin {cases} x, x> 0 \\ 0, x <0 \ end {cases} $$ display $$
ReLU a commencé à être massivement utilisé après 2011, lorsque l'article «Deep Sparse Rectifier Neural Networks» a été publié. Cependant, une telle fonction était auparavant connue. Le concept de «puissance d'activation» est applicable à ReLU (pour plus de détails, voir le livre «Deep Learning. Immersion dans le monde des réseaux de neurones»). Mais la principale caractéristique qui rend ReLU plus attrayant que les autres fonctions d'activation est son calcul dérivé simple:
$$ display $$ d (ReLU (x)) = \ begin {cases} 1, x> 0 \\ 0, x <0 \ end {cases} $$ display $$
Ainsi, ReLU est plus efficace sur le plan informatique que les autres fonctions d'activation (sigmoïde, tangente hyperbolique, etc.).
Couche entièrement connectée
Il est maintenant temps de discuter d'une couche entièrement connectée. Le plus important de tous les autres, car c'est dans cette couche que se trouvent tous les poids, qui doivent être paramétrés pour que le réseau neuronal fonctionne bien. Une couche entièrement connectée est simplement une matrice de poids:
$$ afficher $$ W = | w_ {i, j} | $$ afficher $$
Une nouvelle représentation interne est obtenue lorsque la matrice de poids est multipliée par la colonne d'entrée:
$$ afficher $$ \ boldsymbol {x} _ {nouveau} = W \ cdot \ boldsymbol {x} $$ afficher $$
O Where
$ inline $ \ boldsymbol {x} $ inline $ a la taille
$ inline $ input \ _shape $ inline $ et
$ inline $ x_ {new} $ inline $ -
$ inline $ output \ _shape $ inline $ . Par exemple
$ inline $ \ boldsymbol {x} $ inline $ - vecteur 784 dimensions, et
$ inline $ \ boldsymbol {x} _ {new} $ inline $ Est un vecteur à 100 dimensions, alors la matrice W a une taille de 100x784. Il se trouve que sur cette couche est 100x784 = 78 400 poids.
Avec la rétropropagation de l'erreur, il faut prendre la dérivée par rapport à chaque poids de cette matrice. Simplifiez le problème et ne prenez que la dérivée par rapport à
$ inline $ w_ {1,1} $ inline $ . Lors de la multiplication de la matrice et du vecteur, le premier élément du nouveau vecteur
$ inline $ \ boldsymbol {x} _ {new} $ inline $ est égal à
$ inline $ x_ {new ~ 1} = w_ {1,1} \ cdot x_1 + ... + w_ {1,784} \ cdot x_ {784} $ inline $ et le dérivé
$ inline $ x_ {new ~ 1} $ inline $ par
$ inline $ w_ {1,1} $ inline $ sera simple
$ en ligne $ x_1 $ en ligne $ , il vous suffit de prendre le dérivé du montant ci-dessus. Il en va de même pour tous les autres poids. Mais ce n'est pas un algorithme de propagation de retour d'erreur, tant qu'il ne s'agit que d'une matrice de dérivés. Vous devez vous rappeler que de la couche suivante à celle-ci (l'erreur va de la fin au début) vient un vecteur de gradient à 100 dimensions
$ inline $ d \ boldsymbol {z} $ inline $ . Premier élément de ce vecteur
$ inline $ dz_1 $ inline $ sera multiplié par tous les éléments de la matrice des dérivés qui "ont participé" à la création
$ inline $ x_ {new ~ 1} $ inline $ , c'est-à-dire le
$ en ligne $ x_1, x_2, ..., x_ {784} $ en ligne $ . De même, le reste des éléments. Si vous traduisez cela dans le langage de l'algèbre linéaire, alors c'est écrit comme ceci:
$$ display $$ \ frac {\ partial L} {\ partial W} = (d \ boldsymbol {z}, ~ dW) = \ left (\ begin {matrix} dz_ {1} \ cdot \ boldsymbol {x} \ \ ... \\ dz_ {100} \ cdot \ boldsymbol {x} \ end {matrix} \ right) _ {100} $$ display $$
La sortie est une matrice 100x784.
Vous devez maintenant comprendre quoi transférer vers la couche précédente. Pour cela et pour une meilleure compréhension de ce qui s'est passé maintenant, je veux écrire ce qui s'est passé lors de la prise de dérivés sur cette couche dans un langage légèrement différent, pour échapper aux spécificités de «ce qui est multiplié par» aux fonctions (encore).
Quand je voulais ajuster les poids, je voulais prendre la dérivée de la fonction d'erreur pour ces poids:
$ inline $ \ frac {\ partial L} {\ partial W} $ inline $ . Il a été montré ci-dessus comment prendre des dérivées des fonctions d'erreur et des fonctions d'activation. Par conséquent, nous pouvons considérer un tel cas (en
$ inline $ d \ boldsymbol {z} $ inline $ toutes les dérivées de la fonction d'erreur et des fonctions d'activation sont déjà en place):
$$ afficher $$ \ frac {\ partial L} {\ partial W} = d \ boldsymbol {z} \ cdot \ frac {\ partial \ boldsymbol {x} _ {new} (W)} {\ partial W} $ $ afficher $$
Cela peut être fait, car vous pouvez envisager
$ inline $ \ boldsymbol {x} _ {new} $ inline $ en fonction de W:
$ inline $ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} $ inline $ .
Vous pouvez remplacer cela dans la formule ci-dessus:
$$ afficher $$ \ frac {\ partial L} {\ partial W} = d \ boldsymbol {z} \ cdot \ frac {\ partial W \ cdot \ boldsymbol {x}} {\ partial W} = d \ boldsymbol { z} \ cdot E \ cdot \ boldsymbol {x} $$ display $$
Où E est une matrice composée d'unités (PAS une matrice d'unités).
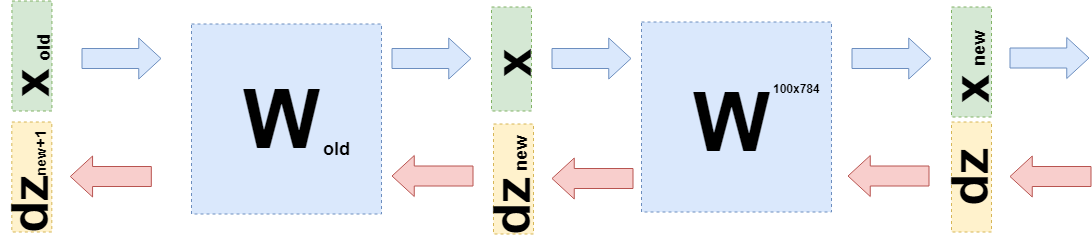
Maintenant, lorsque vous devez prendre la dérivée de la couche précédente (même si pour la simplicité des calculs, ce sera également une couche entièrement connectée, mais dans le cas général, cela ne change rien), alors vous devez considérer
$ inline $ \ boldsymbol {x} $ inline $ en fonction de la couche précédente
$ inline $ \ boldsymbol {x} (W_ {old}) $ inline $ :
$$ afficher $$ \ begin {réunis} \ frac {\ partial L} {\ partial W_ {old}} = d \ boldsymbol {z} \ cdot \ frac {\ partial \ boldsymbol {x} _ {nouveau} (W )} {\ partial W_ {old}} = d \ boldsymbol {z} \ cdot \ frac {\ partial W \ cdot \ boldsymbol {x} (W_ {old})} {\ partial W_ {old}} = \\ = d \ boldsymbol {z} \ cdot \ frac {\ partial W \ cdot W_ {old} \ cdot \ boldsymbol {x} _ {old}} {\ partial W_ {old}} = d \ boldsymbol {z} \ cdot W \ cdot E \ cdot \ boldsymbol {x} _ {old} = \\ = d \ boldsymbol {z} _ {new} \ cdot E \ cdot \ boldsymbol {x} _ {old} \ end {réunis} $$ afficher $$
Exactement
$ inline $ d \ boldsymbol {z} _ {new} = d \ boldsymbol {z} \ cdot W $ inline $ et vous devez envoyer à la couche précédente.
Code
Cet article vise principalement à expliquer les mathématiques des réseaux de neurones. Je vais consacrer très peu de temps au code.
Voici un exemple d'implémentation de la fonction d'erreur:
class CrossEntropy: def forward(self, y_true, y_hat): self.y_hat = y_hat self.y_true = y_true self.loss = -np.sum(self.y_true * np.log(y_hat)) return self.loss def backward(self): dz = -self.y_true / self.y_hat return dz
La classe a des méthodes pour le passage direct et inverse. Au moment de la passe directe, l'instance de classe stocke les données à l'intérieur de la couche et, au moment de la passe de retour, elle les utilise pour calculer le gradient. Les couches restantes sont construites de la même manière. Grâce à cela, il devient possible d'écrire un neurone entièrement connecté dans ce style:
class MnistNet: def __init__(self): self.d1_layer = Dense(784, 100) self.a1_layer = ReLu() self.drop1_layer = Dropout(0.5) self.d2_layer = Dense(100, 50) self.a2_layer = ReLu() self.drop2_layer = Dropout(0.25) self.d3_layer = Dense(50, 10) self.a3_layer = Softmax() def forward(self, x, train=True): ... def backward(self, dz, learning_rate=0.01, mini_batch=True, update=False, len_mini_batch=None): ...
Le code complet peut être trouvé
ici .
Je conseille également d'étudier cet
article sur Habré .
Conclusion
J'espère avoir pu expliquer et montrer que les mathématiques assez simples sont derrière les réseaux de neurones et que ce n'est pas du tout effrayant. Néanmoins, pour une compréhension plus approfondie, il vaut la peine d'essayer d'écrire votre propre «vélo». Les corrections et suggestions sont heureuses de lire dans les commentaires.